जुड़वां प्रमुख परिकल्पना गणित में सबसे महत्वपूर्ण और जटिल मुद्दों में से एक है। दो गणितज्ञों ने छोटे संख्यात्मक प्रणालियों के लिए इस समस्या का एक समानांतर संस्करण हल किया।

7 सितंबर को, दो गणितज्ञों
ने गणित में सबसे प्रसिद्ध खुली समस्याओं में
से एक के एक संस्करण का
प्रमाण प्रकाशित किया। परिणाम
जुड़वां अपराधों की परिकल्पना के अध्ययन में एक नया मोर्चा खोलता है जिसने गणितज्ञों को सौ से अधिक वर्षों से ग्रस्त किया है और अंकगणित के कुछ सबसे गहन गुणों के साथ जुड़ा हुआ है।
ऑक्सफोर्ड के एक गणितज्ञ
जेम्स मेनार्ड ने कहा, "हम लंबे समय से स्किडिंग कर रहे हैं और हम इस कार्य के लिए विचारों से बाहर चल रहे हैं, इसलिए किसी के लिए नए विचारों का होना स्वाभाविक है।"
जुड़वां प्रधान परिकल्पना उन युग्मों के युग्मों पर लागू होती है जो 2 से भिन्न होते हैं। जुड़वाँ संख्या 5 और 7. और 17 और 19 हैं। परिकल्पना में कहा गया है कि प्राकृतिक संख्याओं के बीच इस तरह के जोड़े की अनंत संख्या है। पिछले एक दशक में, गणितज्ञों ने महत्वपूर्ण प्रगति की है, लेकिन वे अभी भी समस्या के पूर्ण समाधान से बहुत दूर हैं।
नए साक्ष्यों के लेखक, कोलम्बिया विश्वविद्यालय के
विल साविन और मैडिसन में विस्कॉन्सिन विश्वविद्यालय के
मार्क शस्टरमैन ने एक छोटी, लेकिन अभी भी ध्यान देने योग्य गणितीय दुनिया के लिए परिकल्पना को साबित किया। उन्होंने परिमित संख्यात्मक प्रणाली के मामले में इसकी वैधता साबित की जिसमें कुछ ही संख्याएँ हैं।
ऐसी संख्या प्रणाली को "परिमित क्षेत्र" कहा जाता है। अपने छोटे आकार के बावजूद, वे अनगिनत पूर्णांक में निहित गणितीय गुणों में से कई को बरकरार रखते हैं। गणितज्ञ परिमित क्षेत्रों में अंकगणित के सवालों के जवाब खोजने की कोशिश कर रहे हैं, और इन परिणामों को सभी पूर्णांकों में अनुवाद करने की उम्मीद करते हैं।
"परम सपना, भले ही थोड़ा भोला हो, यह है कि एक परिमित क्षेत्र के गुणों की अच्छी समझ पूर्णांक की दुनिया पर प्रकाश डाल सकती है," मेयार्ड ने कहा।
जुड़वां अपराधों की परिकल्पना को साबित करने के अलावा, सविन और शस्टरमैन ने छोटे संख्यात्मक प्रणालियों में primes के व्यवहार के बारे में और भी अधिक आश्चर्यजनक परिणाम पाया। उन्होंने सटीक आवृत्ति साबित की जिसके साथ छोटे अंतराल पर जुड़वाँ अपराध दिखाई देते हैं - और इस परिणाम से जुड़वाँ अपराधों जैसी अत्यंत सटीक घटना को नियंत्रित करना संभव हो जाता है। गणितज्ञ सामान्य संख्या के साथ समान परिणाम प्राप्त करने का सपना देखते हैं; वे संख्या रेखा पर अभाज्य संख्याओं पर लागू विचारों की खोज में नए साक्ष्य तलाशते हैं।
एक नई तरह का प्राइम
ट्विन प्राइम परिकल्पना की सबसे प्रसिद्ध भविष्यवाणी संख्याओं के एक असीम रूप से बड़ी संख्या में मौजूदगी है जो 2. से भिन्न होती है। हालांकि, यह कथन अधिक सामान्य है। यह कहता है कि अनंत की एक संख्या है जो 4 से भिन्न होती है (उदाहरण के लिए, 3 और 7), या 14 (293 और 307), या आपके द्वारा निर्दिष्ट किसी भी संख्या से।
अल्फोंस डी पोलिग्नैक
ने 1849 में अपने आधुनिक रूप में
यह धारणा बनाई । अगले 160 वर्षों में, गणितज्ञों ने उसके साथ अधिक प्रगति नहीं की। हालांकि, 2013 में, बर्फ टूट गया, या कम से कम गंभीरता से टूट गया। उस वर्ष,
झांग ईथन ने
अपराधों की एक बड़ी संख्या में मौजूदगी को साबित किया, जिसमें 70 मिलियन से अधिक अंतर नहीं था। अगले साल, मेयार्ड और
टेरी ताओ सहित अन्य गणितज्ञों ने इस अंतर को गंभीरता से कम कर दिया। वर्तमान रिकॉर्ड एक असीम रूप से बड़ी संख्या में primes जोड़े के अस्तित्व का प्रमाण है जो एक दूसरे से 246 से अधिक नहीं हैं।
हालाँकि, उसके बाद, प्रगति थम गई। गणितज्ञ इस समस्या को पूरी तरह से हल करने के लिए एक नए विचार की आवश्यकता को समझते हैं। और इस विचार को देखने के लिए परिमित संख्या प्रणाली एक अच्छी जगह है।
एक परिमित क्षेत्र का निर्माण करने के लिए, आपको सबसे पहले प्राकृतिक संख्याओं से परिमित संख्याओं को निकालना होगा। उदाहरण के लिए, आप पहले पांच नंबर (या कोई भी प्राइम नंबर) ले सकते हैं। और एक संख्या रेखा पर संख्याओं का प्रतिनिधित्व करने के बजाय, हमेशा की तरह, एक डायल के रूप में एक नई संख्या प्रणाली की कल्पना करें।
अंकगणित, जैसा कि आपने अनुमान लगाया होगा, एक सीमित स्थान में काम करना शुरू कर देता है। पांच तत्वों से मिलकर एक परिमित संख्यात्मक प्रणाली में 4 + 3 क्या होगा? हम 4 से शुरू करते हैं, तीन डिवीजनों को दक्षिणावर्त गिनते हैं, और 2 पर आते हैं। एक समान तरीके से घटाव, गुणा और भाग काम करते हैं।

लेकिन केवल एक पकड़ है। परिमित क्षेत्रों में, प्राइम की सामान्य परिभाषा का कोई मतलब नहीं है। अंतिम क्षेत्र पर, किसी भी संख्या को किसी अन्य द्वारा विभाजित किया जाता है। उदाहरण के लिए, 7 आमतौर पर 3 से विभाज्य नहीं है। लेकिन पांच तत्वों के अंतिम क्षेत्र पर, यह विभाज्य है। ऐसा इसलिए है क्योंकि इस अंतिम क्षेत्र पर अंक 7 नंबर 12 के बराबर है - वे दोनों डायल के 2 निशान पर समाप्त होते हैं। इसलिए, 3 से विभाजित 7, 3 द्वारा विभाजित 12 के समान होगा - और 3 से विभाजित 12 4 देगा।
इसलिए, परिमित क्षेत्रों के लिए जुड़वां अपराधों की परिकल्पना सरल बहुपद का उल्लेख करती है - जैसे गणितीय अभिव्यक्तियाँ, उदाहरण के लिए, x
2 + 1।
उदाहरण के लिए, मान लीजिए कि आपके अंतिम क्षेत्र में 1, 2 और 3 संख्याएँ हैं। ये संख्याएँ इस परिमित क्षेत्र में बहुपद के गुणांक होंगी, और "सरल" बहुपद एक होगा जिसे बहुपद कारकों में नहीं बदला जा सकता है। इसलिए, x
2 + x + 2 सरल होगा, क्योंकि इसे कारक नहीं बनाया जा सकता है, लेकिन x
2 - 1 नहीं होगा: यह (x + 1) और (x - 1) का गुणनफल है।
सरल बहुपद परिभाषित करने के बाद, सरल जुड़वां बहुपद के बारे में एक प्रश्न पूछना स्वाभाविक है - बहुपद के जोड़े जो सरल हैं और एक निश्चित मूल्य से भिन्न हैं। उदाहरण के लिए, बहुपद x
2 + x + 2 सरल है, जैसे x
2 + 2x + 2. वे x से भिन्न होते हैं।
परिमित क्षेत्रों के लिए सरल जुड़वां बहुपद की परिकल्पना सरल जुड़वा बहुपद के जोड़े के असीम रूप से बड़ी संख्या के अस्तित्व को इंगित करती है जो न केवल एक्स, बल्कि किसी भी मूल्य से भिन्न होती हैं।
नीट में कटौती
परिमित क्षेत्र और सरल बहुपद की अवधारणाएं दूर की कौड़ी लग सकती हैं, और संख्याओं के गुणों का अध्ययन करने के लिए बेकार है। लेकिन वे एक तूफान सिम्युलेटर की तरह दिखते हैं - अपने आप में एक ब्रह्मांड, एक बड़ी दुनिया में होने वाली घटनाओं के बारे में विचार दे रहा है।
"पूर्णांक और बहुपद के बीच एक प्राचीन सादृश्य है, जो हमें पूर्णांक से संबंधित संभावित अत्यंत जटिल समस्याओं को बहुपद से संबंधित समस्याओं में परिवर्तित करने की अनुमति देता है, जो संभावित रूप से जटिल भी हैं, लेकिन हल करना आसान हो सकता है," शस्टरमैन ने कहा।
परिमित क्षेत्र 1940 में प्रसिद्ध हुए जब
आंद्रे वेल ने छोटी संख्या प्रणाली के अंकगणित को पूर्णांकों के अंकगणित में अनुवाद करने का सटीक तरीका विकसित किया। Weil ने अद्भुत परिणामों के साथ इस संबंध का उपयोग किया। उन्होंने
साबित किया , शायद, गणित में सबसे महत्वपूर्ण समस्या - रीमैन परिकल्पना - परिमित क्षेत्रों पर घटता के एक सेट के साथ मामले के लिए (यह समस्या रीमैन ज्यामितीय परिकल्पना के नाम से जानी जाती है)। इस प्रमाण ने अतिरिक्त
वीइल परिकल्पनाओं के एक सेट के साथ
, परिमित क्षेत्रों को गणितीय खोजों के लिए एक समृद्ध परिदृश्य बना दिया।
वील का प्रमुख विचार यह था कि परिमित क्षेत्रों में, संख्याओं के बारे में प्रश्नों के उत्तर खोजने के लिए ज्यामितीय तकनीकों का उपयोग किया जा सकता है। “यह परिमित क्षेत्रों की एक विशेषता है। कई कार्य जिन्हें आप हल करना चाहते हैं, उन्हें ज्यामितीय रूप से फिर से परिभाषित किया जा सकता है, ”शस्टरमैन ने कहा।
यह समझने के लिए कि ऐसे वातावरण में ज्यामिति कैसे दिखाई देती है, प्रत्येक बहुपद को अंतरिक्ष में एक बिंदु के रूप में कल्पना करें। एक बहुपद के गुणांक निर्देशांक के रूप में कार्य करते हैं जो इसके स्थान को निर्धारित करते हैं। 1, 2, और 3 के हमारे अंतिम क्षेत्र में लौटकर, बहुपद 2x + 3 द्वि-आयामी अंतरिक्ष के बिंदु (2, 3) पर स्थित है।
लेकिन सबसे सरल परिमित स्थान में भी बहुपद की अनंत संख्या होती है। सबसे बड़े प्रतिपादक, या अभिव्यक्ति की डिग्री के विस्तार को बढ़ाकर अधिक जटिल बहुपद बनाया जा सकता है। हमारे मामले में, बहुपद x
2 - 3x - 1 को त्रि-आयामी अंतरिक्ष में एक बिंदु द्वारा दर्शाया जाएगा। और बहुपद 3x
7 + 2x
6 + 2x
5 - 2x
4 - 3x
3 + x
2 - 2x + 3 को आठ-आयामी अंतरिक्ष में एक डॉट द्वारा दर्शाया जाएगा।
नए काम में, यह ज्यामितीय स्थान किसी दिए गए परिमित क्षेत्र के लिए दी गई डिग्री के सभी बहुपद का प्रतिनिधित्व करता है। प्रश्न निम्नलिखित में बदल जाता है: क्या सरल पॉलीओनियल को दर्शाते हुए सभी बिंदुओं को अलग करने का एक तरीका है?
सविन और शस्टरमैन की रणनीति अंतरिक्ष को दो भागों में विभाजित करने की है। एक भाग में कारकों की एक समान संख्या के साथ बहुपद के अनुरूप सभी बिंदु होंगे। दूसरे में, विषम संख्या वाले कारकों के साथ बहुपद के अनुरूप सभी बिंदु।
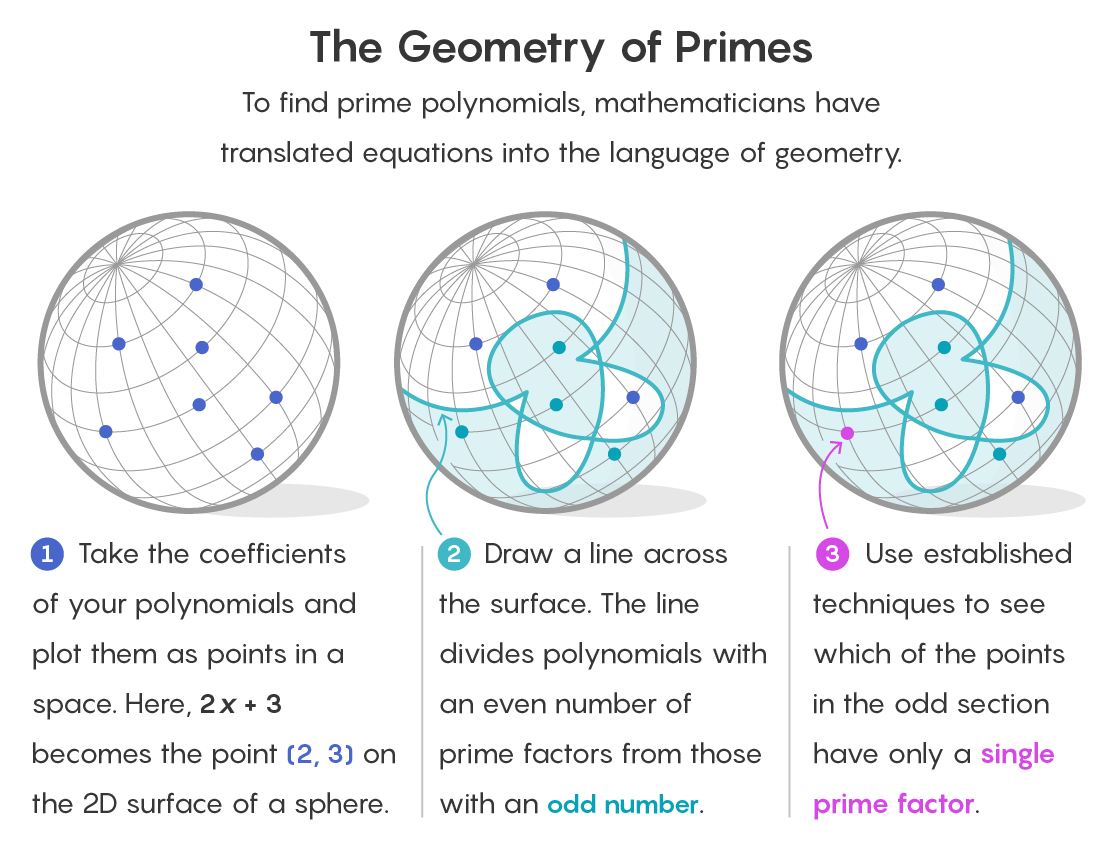
यह पहले से ही कार्य को सरल बनाता है। परिमित क्षेत्रों के लिए सरल जुड़वां बहुपद की परिकल्पना केवल एक कारक के साथ बहुपद के लिए लागू होती है (जैसे एक अभाज्य का एक कारक होता है, वह स्वयं भी होता है)। और चूंकि संख्या 1 विषम है, इसलिए समान कारकों के साथ बहुपद वाले स्थान का हिस्सा तुरंत त्याग दिया जा सकता है।
विभाजन का उपयोग करने की चाल है। उदाहरण के लिए, द्वि-आयामी वस्तु के मामले में, एक गोले की सतह, इसे एक आयामी वक्र द्वारा आधे में काट दिया जाता है - जिस तरह भूमध्य रेखा पृथ्वी की सतह को काटती है। एक बड़ी संख्या में आयाम वाली वस्तु को हमेशा एक वस्तु से काटा जा सकता है, जिसमें आयामों की संख्या कम होती है।
लेकिन बहुपदों के स्थान को विभाजित करते हुए कम आयाम वाले ये रूप भूमध्य रेखा के समान सुरुचिपूर्ण नहीं हैं। उन्हें एक गणितीय सूत्र के अनुसार तैयार किया जाता है
जिसे मोबियस फ़ंक्शन कहा जाता
है । इनपुट पर, यह एक बहुपद लेता है, और आउटपुट पर यह 1 देता है यदि बहुपद में समान कारकों की संख्या है, -1, यदि इसकी विषम संख्या है, और 0 यदि यह कारक है (16 के बाद से 2 × पर विघटित हो सकता है) 2 × 2 × 2)।
मोबियस फ़ंक्शन द्वारा खींचे गए मोड़ मोड़ की तरह मुड़ते हैं और पागल की तरह मुड़ते हैं, कई जगहों पर खुद के साथ घूमते हैं। इन स्थानों, जिन्हें विलक्षणता कहा जाता है, विशेष रूप से विश्लेषण करना मुश्किल है (वे बहुपद के अनुरूप होते हैं जिन्हें कई समान प्राइमरों में विघटित किया जा सकता है)।
सविन और शस्टरमैन का मौलिक नवाचार यह था कि उन्हें कम माप के साथ छोरों को काटने का सटीक तरीका मिला। ये सेगमेंट पूरे लूप की तुलना में सीखना आसान था।
एक विषम संख्या वाले प्रमुख कारकों के साथ बहुपदों की सूची तैयार की - और यह सबसे कठिन था - सविन और शस्टरमैन ने यह निर्धारित करने के कार्य का सामना किया कि कौन से सरल हैं और कौन से जुड़वां हैं। ऐसा करने के लिए, उन्होंने गणितज्ञों द्वारा उपयोग किए जाने वाले कई सूत्र लागू किए, जो सामान्य लोगों के बीच प्रमुख संख्याओं का अध्ययन करते हैं।
सविन और शस्टरमैन ने अपनी तकनीक का उपयोग कुछ महत्वपूर्ण क्षेत्रों में सरल बहुपद के संबंध में दो महत्वपूर्ण बिंदुओं को साबित करने के लिए किया।
सबसे पहले, परिमित क्षेत्रों में जुड़वां अपराधों की परिकल्पना सत्य है: आमतौर पर जुड़वां बहुपत्नी के कई जोड़े होते हैं जो किसी भी दिए गए मूल्य से भिन्न होते हैं।
दूसरे, और इससे भी महत्वपूर्ण बात यह है कि यह कार्य सरल जुड़वा बहुपद की संख्या की एक सटीक गणना प्रदान करता है जो एक निश्चित क्रम के बहुपद के बीच पाया जा सकता है। यह जानने के लिए अनुरूप है कि किसी संख्या रेखा पर किसी भी पर्याप्त लंबे अंतराल के भीतर कितने जुड़वां प्राइम हैं - और यह सिर्फ गणितज्ञों का सपना है।
तेल अवीव विश्वविद्यालय के ज़िव रुडनिक ने कहा, "यह पहला काम है जो पूर्णांक के लिए मात्रात्मक सादृश्य देता है, जो पूर्णांकों के लिए सही होना चाहिए और यह वास्तव में उत्कृष्ट परिणाम है।" "अब तक, ऐसा कुछ नहीं हुआ है।"
साविन और शस्टरमैन के प्रमाण से पता चलता है कि, आंद्रे वेल के लगभग 80 साल बाद, परिमित क्षेत्रों पर घटता के लिए रीमैन की परिकल्पना साबित हुई, गणितज्ञ अभी भी इस दिशा में सख्ती से आगे बढ़ रहे हैं। अब, गणितज्ञ जो जुड़वां प्रधान परिकल्पना के साथ काम करते हैं, वे सविन और शस्टरमैन के काम की ओर मुड़ेंगे और शायद यह उन्हें प्रेरणा का एक गहरा स्रोत देगा।