क्या होगा अगर बिना पायथन? मशीन सीखने के लिए जूलिया और आम तौर पर

हम हमेशा जल्दी से कोड लिखना चाहते हैं, लेकिन आपको इसके लिए भुगतान करना होगा। सामान्य उच्च-स्तरीय लचीली भाषाओं में, प्रोग्राम जल्दी से विकसित किए जा सकते हैं, लेकिन वे लॉन्च के बाद धीरे-धीरे चलते हैं। उदाहरण के लिए, शुद्ध अजगर में कुछ भारी पढ़ने के लिए यह राक्षसी रूप से धीमा है। सी जैसी भाषाएं बहुत तेज़ी से काम करती हैं, लेकिन उनमें गलतियाँ करना आसान होता है, जिसकी खोज से गति में सभी लाभ कम हो जाएंगे।

आमतौर पर यह दुविधा निम्नानुसार हल की जाती है: पहले वे कुछ लचीलेपन पर एक प्रोटोटाइप लिखते हैं, उदाहरण के लिए, पायथन या आर पर, और फिर इसे C / C ++ या फोरट्रान पर फिर से लिखते हैं। लेकिन यह चक्र बहुत लंबा है, क्या आप इसके बिना कर सकते हैं?



शायद कोई उपाय है। जूलिया एक उच्च-स्तरीय और लचीला अभी तक तेज प्रोग्रामिंग भाषा है। जूलिया के पास कई प्रेषण, एक एकीकृत स्मार्ट कंपाइलर और मेटाप्रोग्रामिंग उपकरण हैं। Gleb Ivashkevich ( phtRaveller ), डेटारीथेमिक्स के संस्थापक, जो उद्योग और अन्य उद्योगों के लिए मशीन लर्निंग सिस्टम विकसित करता है, एक पूर्व भौतिक विज्ञानी, आपको जूलिया के बारे में और अधिक बताएगा।

Gleb समझाएगा कि नई भाषाओं की आवश्यकता क्यों है और कभी-कभी पायथन क्यों गायब है। वह आपको बताएगा कि जूलिया में क्या दिलचस्प है, इसकी ताकत और कमजोरियों के बारे में, अन्य भाषाओं के साथ तुलना करें, और दिखाएं कि भाषा में मशीन सीखने और सामान्य रूप से कंप्यूटिंग की संभावना क्या है।

अस्वीकरण। कोई वाक्यविन्यास पार्सिंग नहीं होगा। हब्राज़िटेली ने अनुभवी डेवलपर्स का अनुभव किया है, इसलिए यह उदाहरण के लिए लूप लिखने का कोई मतलब नहीं है।

दो भाषाओं की समस्या

यदि आप कोड फास्ट लिखते हैं, तो प्रोग्राम धीरे-धीरे चलते हैं। यदि प्रोग्राम तेजी से काम करते हैं, तो उन्हें लंबे समय तक लिखें।

क्लासिक पायथन पहली श्रेणी में आता है। यदि आप NumPy को हटाते हैं, तो धीरे-धीरे शुद्ध पायथन में कुछ पर विचार करें। दूसरी ओर, C और C ++ जैसी भाषाएं हैं। एक संतुलन खोजना मुश्किल है, इसलिए अक्सर वे पहले कुछ लचीलेपन पर एक प्रोटोटाइप लिखते हैं, और एल्गोरिथ्म को डीबग करने के बाद, वे इसे तेजी से भाषा में लिखते हैं। यह दो भाषाओं में स्पष्ट समस्या का एक उदाहरण है: एक लंबा चक्र जब आपको पायथन में लिखना है, और इसे सी या साइथन में फिर से लिखना है, उदाहरण के लिए।

मशीन लर्निंग और डेटा साइंस के स्पेशलिस्ट्स में NumPy, Sklearn, TensorFlow है। वे सी में एक एकल पंक्ति के बिना वर्षों से अपनी समस्याओं को हल कर रहे हैं, और ऐसा लगता है कि दो भाषाओं की समस्या उन्हें चिंता नहीं करती है। ऐसा नहीं है, समस्या स्वयं स्पष्ट रूप से प्रकट होती है, क्योंकि NumPy या TensorFlow में कोड वास्तव में पायथन नहीं है। इसका उपयोग मेटलंगज के रूप में किया जाता है जो कि अंदर होता है। अंदर बिल्कुल C / Fortran (NumPy के मामले में) या C ++ (TensorFlow के मामले में) है।

यह "सुविधा" खराब रूप से दिखाई देती है, उदाहरण के लिए, PyTorch में, लेकिन Numpy में यह स्पष्ट रूप से दिखाई देता है। उदाहरण के लिए, यदि गणना में एक क्लासिक पायथन चक्र दिखाई दिया, तो कुछ गलत हो गया। उत्पादक कोड में, छोरों की आवश्यकता नहीं होती है, आपको सब कुछ फिर से लिखना होगा ताकि NumPy इसे वेक्टर कर सके और जल्दी से गणना कर सके।

इसी समय, यह कई लोगों को लगता है कि न्यूमपी तेज है और इसके साथ सब कुछ ठीक है। आइए देखें कि यह देखने के लिए NumPy के पास क्या है।

• NumPy पायथन प्रकार के लचीलेपन की समस्या को ठीक करने की कोशिश कर रहा है, इसलिए इसमें बहुत सख्त प्रकार की प्रणाली है । यदि सरणी का एक निश्चित प्रकार है, तो इसमें और कुछ नहीं हो सकता है, यदि Float64 है, तो इसके बारे में कुछ भी नहीं किया जा सकता है।
• भेजने। सरणियों के प्रकार और आपको किस ऑपरेशन को करने की आवश्यकता पर निर्भर करता है, खुद के अंदर NumPy यह तय करेगा कि गणना करने के लिए जितनी जल्दी हो सके कॉल करने के लिए कौन सा फ़ंक्शन है। लाइब्रेरी क्लासिक पायथन को संगणना पाश से बाहर निकालने की कोशिश करेगी।

यह पता चला है कि Numpy उतना तेज़ नहीं है जितना लगता है। यही कारण है कि साइथॉन या नुम्बा जैसी परियोजनाएं हैं। पहला पायथन और सी के "हाइब्रिड" से सी-कोड उत्पन्न करता है, और दूसरा पायथन में कोड को संकलित करता है और आमतौर पर यह तेजी से होता है।

अगर नुम्पी वास्तव में उतनी ही तेज थी, जितना कि बहुतों को लगता है, तो साइथन और नुम्बा के अस्तित्व का कोई मतलब नहीं होगा।

हम साइथॉन में सब कुछ फिर से लिखते हैं अगर हम जल्दी से कुछ बड़ा और जटिल खोजना चाहते हैं। साइथन में एक आवरण की गुणवत्ता के लिए मानदंडों में से एक उत्पन्न कोड में शुद्ध पायथन कॉल की उपस्थिति या अनुपस्थिति है।

एक सरल उदाहरण: हम प्रकार (अच्छा) जोड़ते हैं या जोड़ते नहीं हैं (खराब), और हमें दो पूरी तरह से अलग कोड मिलते हैं, हालांकि प्रकारों के अलावा प्रारंभिक विकल्प अलग नहीं हैं।



जब हम C कोड उत्पन्न करते हैं, तो पहले मामले में हमें निम्नलिखित मिलते हैं:

 __pyx_t_4 = __pyx_v_i; __pyx_v_result = (__pyx_v_result + (*((double *) ( /* dim=0 */ (__pyx_v_a.data + __pyx_t_4 * __pyx_v_a.strides[0]) )))); 

और दूसरे result =0. इस में बदल जाएगा:

 __pyx_t_6 = PyFloat_FromDouble((*((double *) ( /* dim=0 */ (__pyx_v_a.data + __pyx_t_4 * __pyx_v_a.strides[0]) )))); if (unlikely(!__pyx_t_6)) __PYX_ERR(0, 9, __pyx_L1_error) __Pyx_GOTREF(__pyx_t_6); __pyx_t_7 = PyNumber_InPlaceAdd(__pyx_v_result, __pyx_t_6); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 9, __pyx_L1_error) __Pyx_GOTREF(__pyx_t_7); __Pyx_DECREF(__pyx_t_6); __pyx_t_6 = 0; __Pyx_DECREF_SET(__pyx_v_result, __pyx_t_7); __pyx_t_7 = 0; 

जब एक प्रकार निर्दिष्ट किया जाता है, तो सी कोड तेज गति से चलता है। यदि प्रकार निर्दिष्ट नहीं किया गया है, तो हम सामान्य पायथन देखते हैं, लेकिन सी साइड से: मानक पायथन कॉल, जहां किसी कारण से double से float बनाए जाते हैं, लिंक गिने जाते हैं, और बहुत सारे कचरा कोड। यह कोड धीमा है क्योंकि यह हर ऑपरेशन के लिए पायथन को बुलाता है।

क्या एक ही बार में सभी समस्याओं को हल करना संभव है

यह मजेदार है कि जब हम किसी चीज के बारे में सोचते हैं, तो हम शुद्ध पायथन को हटाने की कोशिश करते हैं। ऐसा करने के लिए दो विकल्प हैं।

• साइथन या अन्य उपकरणों का उपयोग करना। ऐसे कई तरीके हैं जिनसे आप अपने साइथॉन कोड को लगभग किसी भी पायथन कॉल के साथ समाप्त कर सकते हैं। लेकिन यह सबसे सुखद गतिविधि नहीं है: साइथन में सब कुछ इतना स्पष्ट नहीं है, और केवल कुछ ही समय व्यतीत होता है यदि आप सी में सब कुछ लिखते हैं, तो परिणामस्वरूप मॉड्यूल का उपयोग पायथन में किया जा सकता है, लेकिन फिर भी इसमें लंबा समय लगता है, त्रुटियां होती हैं, कोड हमेशा स्पष्ट नहीं होता है और यह हमेशा स्पष्ट नहीं होता है कि इसे कैसे अनुकूलित किया जाए।
• Numba का उपयोग करना, जो एक JIT संकलन करता है।

लेकिन शायद एक बेहतर तरीका है, और मुझे लगता है कि यह जूलिया है ।

जूलिया

रचनाकारों का दावा है कि यह एक तेज , उच्च-स्तरीय और लचीली भाषा है, जो कोड लिखने में आसानी के मामले में पायथन की तुलना में है। मेरी राय में, जूलिया एक स्क्रिप्टिंग भाषा की तरह है : आपको सी में जो करना है, वह करने की ज़रूरत नहीं है, जहां डेटा संरचनाओं सहित सब कुछ बहुत कम-स्तर है। उसी समय, आप एक नियमित कंसोल में काम कर सकते हैं, जैसे कि पायथन और अन्य भाषाओं के साथ।

जूलिया जस्ट-इन-टाइम संकलन का उपयोग करता है - यह उन तत्वों में से एक है जो गति देता है। लेकिन भाषा गणना के साथ अच्छी है, क्योंकि यह उनके लिए विकसित की गई थी। जूलिया का उपयोग वैज्ञानिक कार्यों के लिए किया जाता है और उन्हें अच्छा प्रदर्शन मिलता है।

यद्यपि जूलिया एक सामान्य-उद्देश्य वाली भाषा की तरह लगने की कोशिश कर रही है, जूलिया कंप्यूटिंग के लिए अच्छा है और वेब सेवाओं के लिए बहुत अच्छा नहीं है। उदाहरण के लिए, Django के बजाय जूलिया का उपयोग करना सबसे अच्छा विकल्प नहीं है।

आइए भाषा की विशेषताओं को एक आदिम फ़ंक्शन के उदाहरण के रूप में देखें।

 function f(x) α = 1 + 2x end julia> methods(f) # 1 method for generic function "f": [1] f(x) in Main at mpconf.jl:2 

इस कोड में चार विशेषताएं ध्यान देने योग्य हैं।

• यूनिकोड के उपयोग पर व्यावहारिक रूप से कोई प्रतिबंध नहीं है । आप गहरी शिक्षा या संख्यात्मक मॉडलिंग पर एक लेख से सूत्र ले सकते हैं, एक ही वर्ण के साथ फिर से लिख सकते हैं, और सब कुछ काम करेगा - यूनिकोड लगभग हर जगह सिलना है।
• कोई गुणन चिह्न नहीं है। हालांकि, इसके बिना करना हमेशा संभव नहीं होता है, उदाहरण के लिए, 2.x (एक फ्लोटिंग-पॉइंट नंबर एक्स) जूलिया कसम खाएगी।
• कोई return नहीं । सामान्य तौर पर, यह अनुशंसा की जाती है कि आप return लिखें ताकि आप देख सकें कि क्या हो रहा है, लेकिन उदाहरण α वापस आ जाएगा, क्योंकि असाइनमेंट एक अभिव्यक्ति है।
• कोई प्रकार नहीं । ऐसा लगता है कि अगर गति है, तो किसी बिंदु पर प्रकार दिखाई देने चाहिए? हां, वे दिखाई देंगे, लेकिन बाद में।

जूलिया में तीन विशेषताएं हैं जो लचीलापन और गति देते हैं: कई प्रेषण, मेटाप्रोग्रामिंग और समानांतरवाद । हम पहले दो के बारे में बात करेंगे, और उन्नत उपयोगकर्ताओं के लिए स्वतंत्र अध्ययन के लिए समानांतर छोड़ देंगे।

एकाधिक शेड्यूलिंग

उपरोक्त उदाहरण में methods(f) लिए कॉल अप्रत्याशित रूप से दिखता है - फ़ंक्शन के किस प्रकार के तरीके हैं? हम इस तथ्य के लिए उपयोग किए जाते हैं कि हमारे पास कक्षा की वस्तुएं हैं, कक्षाओं में विधियां हैं। लेकिन जूलिया में सब कुछ अंदर बाहर कर दिया गया है: कार्यों के तरीके हैं, क्योंकि भाषा कई प्रेषण का उपयोग करती है।

मल्टीपल शेड्यूलिंग का अर्थ है कि किसी विशेष फ़ंक्शन के वेरिएंट को निष्पादित किया जाएगा जो इस फ़ंक्शन के पैरामीटर प्रकारों के पूरे सेट से निर्धारित होता है।

मैं संक्षेप में वर्णन करूंगा कि यह पहले से ही परिचित उदाहरण पर कैसे काम करता है।

 function f(x) α = 1 + 2x end function f(x::AbstractFloat) α = 1 + sin(x) end julia> methods(f) # 2 methods for generic function "f": [1] f(x::AbstractFloat) in Main at mpconf.jl:6 [2] f(x) in Main at mpconf.jl:2 

विभिन्न प्रकार के सेट के लिए एक ही फ़ंक्शन के वेरिएंट को विधियां कहा जाता है। कोड में दो हैं: सभी फ़्लोटिंग-पॉइंट संख्याओं के लिए पहला, और दूसरा सब कुछ के लिए। जब हम पहले फ़ंक्शन को कॉल करते हैं, तो जूलिया तय करेगी कि किस पद्धति का उपयोग करना है और क्या इसे संकलित करना है। यदि यह पहले से ही बुलाया और संकलित किया गया है, तो यह वह है जो ले जाएगा।

चूंकि जूलिया में सब कुछ वैसा नहीं है जैसा हम इस्तेमाल करते हैं, यहां आप उपयोगकर्ता-परिभाषित प्रकारों के लिए फ़ंक्शंस जोड़ सकते हैं, लेकिन ये ओओपी के अर्थ में टाइप तरीके नहीं होंगे। यह केवल वह फ़ील्ड होगा जिसमें फ़ंक्शन लिखा जाता है, क्योंकि फ़ंक्शन समान पूर्ण-पूर्ण ऑब्जेक्ट है जैसा कि बाकी सब कुछ है।

यह पता लगाने के लिए कि वास्तव में क्या ट्रिगर किया जाएगा, विशेष मैक्रोज़ हैं। वे @ शुरू करते हैं। उदाहरण में, @which मैक्रो @which यह पता लगाने की अनुमति देता है @which किसी विशिष्ट मामले के लिए किस पद्धति को बुलाया गया था।



पहले मामले में, जूलिया ने फैसला किया कि चूंकि 2 पूर्णांक है, इसलिए यह AbstractFloat फिट नहीं है, और पहला विकल्प कहा जाता है। दूसरे मामले में, उसने फैसला किया कि यह Float था Float और पहले से ही एक विशेष संस्करण के लिए बुलाया था। यदि आप कुछ विशिष्ट प्रकारों के लिए अन्य विधियाँ जोड़ते हैं तो लगभग यह काम करेगा।

एलएलवीएम और जेआईटी

जूलिया संकलन के लिए LLVM ढांचे का उपयोग करता है। JIT संकलन पुस्तकालय एक भाषा पैक में आता है। पहली बार फ़ंक्शन को बुलाया जाता है, जूलिया यह देखने के लिए देखता है कि क्या फ़ंक्शन इस प्रकार के सेट के साथ उपयोग किया गया है, और यदि आवश्यक हो तो इसे संकलित करता है। पहले लॉन्च में कुछ समय लगेगा, और फिर सब कुछ जल्दी से काम करेगा।

इस पैरामीटर के सेट के लिए पहली कॉल के समय फ़ंक्शन संकलित किया जाएगा।

संकलक सुविधाएँ

• संकलक यथोचित रूप से उचित है क्योंकि एलएलवीएम एक अच्छा उत्पाद है।
• अधिकांश उन्नत डेवलपर्स संकलन प्रक्रिया में देख सकते हैं और देख सकते हैं कि यह क्या उत्पन्न करता है।
• जूलिया और नुम्बा का संकलन समान है । Numba में, आप एक JIT डेकोरेटर भी बनाते हैं, लेकिन Numba में आप इतना "नहीं" प्राप्त कर सकते हैं और यह तय कर सकते हैं कि अनुकूलन या परिवर्तन क्या करना है।

संकलक के कार्य का वर्णन करने के लिए, मैं एक साधारण कार्य का उदाहरण दूंगा:

 function f(x) α = 1 + 3x end julia> @code_llvm f(2) define i64 @julia_f_35897(i64) { top: %1 = mul i64 %0, 3 %2 = add i64 %1, 1 ret i64 %2 } 

मैक्रो @code_llvm आपको पीढ़ी का परिणाम देखने की अनुमति देता है। यह एलएलवीएम आईआर एक मध्यवर्ती प्रतिनिधित्व है , एक प्रकार का कोडांतरक।

कोड में, फ़ंक्शन तर्क को 3 से गुणा किया जाता है, 1 को परिणाम में जोड़ा जाता है, परिणाम वापस आ जाता है। सब कुछ जितना संभव हो उतना सीधा है। यदि आप फ़ंक्शन को थोड़ा अलग तरीके से परिभाषित करते हैं, उदाहरण के लिए, 3 को 2 के साथ बदलें, तो सब कुछ बदल जाएगा।

 function f(x) α = 1 + 2x end julia> @code_llvm f(2) define i64 @julia_f_35894(i64) { top: %1 = shl i64 %0, 1 %2 = or i64 %1, 1 ret i64 %2 } 

ऐसा लगता है, क्या अंतर है: 2, 3, 10? लेकिन जूलिया और एलएलवीएम देखते हैं कि जब आप किसी पूर्णांक के लिए एक फ़ंक्शन कहते हैं, तो आप थोड़ा स्मार्ट हो सकते हैं। दो पूर्णांक से गुणा करना एक बाईं ओर एक बिट है - यह उत्पाद की तुलना में तेज है। लेकिन, ज़ाहिर है, यह केवल पूर्णांकों के लिए काम करता है, यह Float 1 बिट Float बाईं ओर शिफ्ट Float और 2 से गुणा करने का परिणाम प्राप्त Float काम नहीं करेगा।

कस्टम प्रकार

जूलिया में कस्टम प्रकार के रूप में तेजी से निर्मित प्रकार हैं। उन पर एकाधिक शेड्यूलिंग की जाती है, और यह बिल्ट-इन प्रकारों के लिए उतनी ही तेज़ होगी। इस अर्थ में, एकाधिक प्रेषण तंत्र भाषा में गहराई से अंतर्निहित है।

यह उम्मीद करना तर्कसंगत है कि चर का कोई प्रकार नहीं है, केवल मूल्य उनके पास हैं। एक प्रकार के बिना चर केवल एक मार्कर, कुछ कंटेनर पर एक लेबल होता है।

प्रकार प्रणाली पदानुक्रमित है। हम ठोस प्रकारों के वंशज नहीं बना सकते, अमूर्त प्रकार केवल उनके पास हो सकते हैं। हालांकि, अमूर्त प्रकार त्वरित नहीं किया जा सकता है। यह अति सूक्ष्म अंतर सभी के लिए अपील नहीं करेगा।

जैसा कि भाषा के लेखकों ने समझाया कि जब उन्होंने जूलिया विकसित की, तो वे परिणाम प्राप्त करना चाहते थे, और अगर कुछ करना मुश्किल था, तो उन्होंने इसे मना कर दिया। इस तरह के पदानुक्रमित प्रकार की प्रणाली विकसित करना आसान था। यह एक भयावह समस्या नहीं है, लेकिन यदि आप अपना सिर पहले से अंदर की ओर नहीं करते हैं, तो यह असुविधाजनक होगा।

प्रकारों को मानकीकृत किया जा सकता है , जो कि C / C ++ की तरह थोड़ा सा है। उदाहरण के लिए, हमारे पास एक ऐसी संरचना हो सकती है जिसके भीतर क्षेत्र हैं, लेकिन इन क्षेत्रों के प्रकार निर्दिष्ट नहीं हैं - ये पैरामीटर हैं। हम तात्कालिकता पर एक विशिष्ट प्रकार निर्दिष्ट करते हैं।

ज्यादातर मामलों में, प्रकारों को छोड़ दिया जा सकता है । आमतौर पर इनकी जरूरत तब पड़ती है जब टाइप कंपाइलर को यह अनुमान लगाने में मदद करता है कि कंपाइल करना कितना अच्छा है। इस मामले में, प्रकार निर्दिष्ट करने के लिए बेहतर हैं। यदि आप बेहतर प्रदर्शन प्राप्त करना चाहते हैं तो आपको भी प्रकार निर्दिष्ट करने होंगे।

आइए देखें कि क्या संभव है और क्या त्वरित नहीं किया जा सकता है।



पहले प्रकार का AbstractPoint तत्काल नहीं किया जा सकता है। यह सभी के लिए एक सामान्य अभिभावक है जिसे हम उदाहरण के लिए विधियों में निर्दिष्ट कर सकते हैं। दूसरी पंक्ति कहती है कि PlanarPoint{T} इस सार बिंदु का एक वंशज है। खेतों के नीचे शुरू - यहाँ आप पैरामीटर देख सकते हैं। आप यहां एक float , int या अन्य प्रकार रख सकते हैं।

पहला प्रकार त्वरित नहीं किया जा सकता है, और बाकी सभी के लिए वंशज बनाना असंभव है। इसके अलावा, डिफ़ॉल्ट रूप से वे अपरिवर्तनीय हैं । खेतों को बदलने में सक्षम होने के लिए, इसे स्पष्ट रूप से निर्दिष्ट किया जाना चाहिए।

जब सब कुछ तैयार हो जाता है, तो आप जारी रख सकते हैं, उदाहरण के लिए, विभिन्न प्रकार के बिंदुओं के लिए दूरी की गणना करें। उदाहरण में, विमान पर पहला बिंदु PlanarPoint , फिर गोले पर और सिलेंडर पर। किन दो बिंदुओं के आधार पर हम बीच की दूरी की गणना करते हैं, हमें विभिन्न तरीकों का उपयोग करने की आवश्यकता होती है। सामान्य तौर पर, फ़ंक्शन इस तरह दिखेगा:

 function describe(p::AbstractPoint) println("Point instance: $p") end 

Float64 , Float32 , Float16 यह होगा:

 function distance(pf::PlanarPoint{T}, ps::PlanarPoint{T}) where T<:AbstractFloat sqrt((pf.x-ps.x)^2 + (pf.y-ps.y)^2) end 

और पूर्णांकों के लिए, दूरी गणना विधि इस तरह दिखाई देगी:

 function distance(pf::PlanarPoint{T}, ps::PlanarPoint{T}) where T<:Integer abs(pf.x-ps.x) + abs(pf.y-ps.y) end 

प्रत्येक प्रकार के बिंदुओं के लिए, अलग-अलग तरीकों को बुलाया जाएगा।



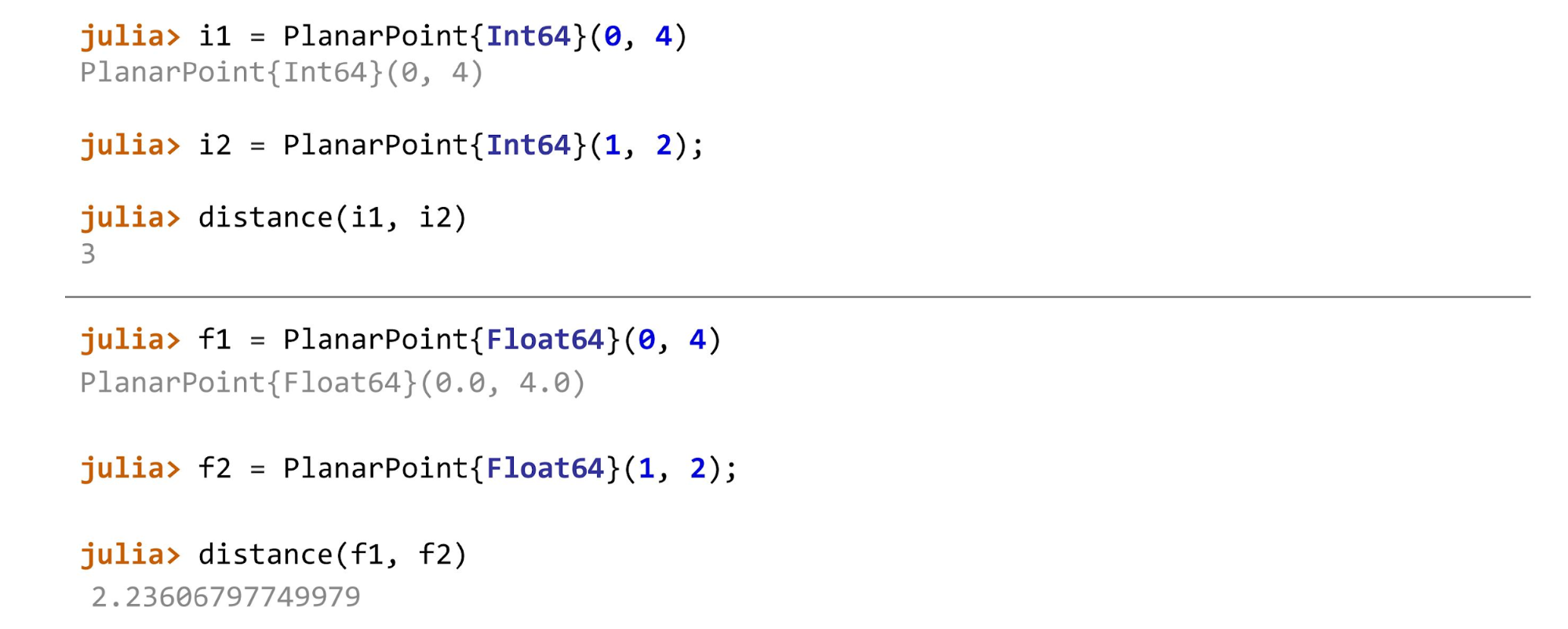
यदि आप धोखा देते हैं और उदाहरण के लिए, distance(f1, i2) लागू करते हैं, तो जूलिया शपथ लेगी: “मुझे यह तरीका नहीं पता है! आपने मुझसे ऐसे तरीके पूछे, और कहा कि वे दोनों एक ही प्रकार के हैं। आपने मुझे यह नहीं बताया कि एक पैरामीटर float होने पर यह कैसे गिना जाता है और दूसरा int । "

गति

आप पहले से ही प्रसन्न थे: “एक जेआईटी संकलन है: लेखन आसान है, यह जल्दी से काम करेगा। पायथन को बाहर फेंको और जूलिया में लिखना शुरू करो! "

लेकिन इतना सरल नहीं है। जूलिया में हर फीचर तेज नहीं होगा। यह दो कारकों पर निर्भर करता है।

• डेवलपर से । ऐसी कोई भाषा नहीं है जिसमें कोई भी कार्य तेजी से हो। एक अनुभवहीन डेवलपर सी में भी कोड लिखेगा जो एक अनुभवी डेवलपर से पायथन कोड की तुलना में बहुत धीमी गति से काम करेगा। किसी भी भाषा की अपनी चाल और बारीकियाँ होती हैं जिन पर प्रदर्शन निर्भर करता है। संकलक, चाहे वह एक नियमित स्थैतिक या JIT हो, सभी बोधगम्य विकल्प प्रदान नहीं कर सकता है और सब कुछ अनुकूलित कर सकता है।
• प्रकार की स्थिरता से । एक तेज संस्करण में, प्रकार से स्थिर होने वाले कार्यों को संकलित किया जाएगा।

स्थिरता लिखें

प्रकार स्थिरता क्या है? जब कंपाइलर पर्याप्त रूप से अनुमान नहीं लगा सकता है कि प्रकारों के साथ क्या होता है, तो इसके लिए बहुत सारे रैपर कोड उत्पन्न करने होते हैं ताकि हर वह चीज जो इनपुट के काम आती है।

प्रकार की स्थिरता को समझने के लिए एक सरल उदाहरण।



मशीन सीखने वाले विशेषज्ञ कहेंगे कि यह एक सामान्य रिले सक्रियण है: यदि x> 0, तो इसे उसी रूप में लौटाएं, अन्यथा शून्य वापस कर दें। प्रश्न चिह्न पूर्णांक के बाद एक समस्या शून्य है। इसका मतलब है कि यदि हम इस फ़ंक्शन को फ़्लोटिंग-पॉइंट नंबर के लिए कहते हैं, तो एक मामले में, एक फ़्लोटिंग-पॉइंट नंबर वापस आ जाएगा, और दूसरे में, एक पूर्णांक।

कंपाइलर केवल फ़ंक्शन तर्क के प्रकार से परिणाम के प्रकार का अनुमान नहीं लगा सकता है। उसे भी अर्थ जानने की जरूरत है। इसलिए, यह बहुत सारे कोड उत्पन्न करता है।

अगला, हम 0 से 1 तक 100 प्रति 100 यादृच्छिक संख्याओं की एक सरणी बनाते हैं, इसे 0.5 से बदलकर सकारात्मक और नकारात्मक संख्याओं को वितरित करते हैं, और परिणाम को मापते हैं। दो दिलचस्प बिंदु हैं: बिंदु और फ़ंक्शन। rand(100,100) बाद डॉट का अर्थ है "प्रत्येक तत्व पर लागू करें।" यदि आपके पास किसी प्रकार का संग्रह और स्केलर फ़ंक्शन है, तो आप इसे समाप्त कर देते हैं, और जूलिया बाकी काम करेंगे। हम मान सकते हैं कि यह एक सामान्य संकलित भाषा में एक सामान्य लूप की तरह प्रभावी है। लिखने के for कोई ज़रूरत नहीं है - सब कुछ आपके लिए किया जाएगा।

बिंदु पर कोई समस्या नहीं हैं - समस्या फ़ंक्शन के अंदर ही है । ऐसे मैट्रिक्स के लिए एक सभ्य कंप्यूटर पर इस तरह के विकल्प का अनुमानित निष्पादन समय माइक्रोसेकंड है। लेकिन वास्तव में - मिलीसेकंड, जो इस तरह के एक छोटे मैट्रिक्स के लिए बहुत अधिक है।

सिर्फ एक लाइन बदलें।



zero(x) फ़ंक्शन निष्पादित करता है तर्क (x) रूप में उसी प्रकार का एक शून्य उत्पन्न करता है। इसका मतलब यह है कि x मान चाहे x , परिणाम का प्रकार हमेशा x के प्रकार से ही जाना जाएगा।

जब हम केवल तर्कों के प्रकार को देखते हैं और पहले से ही परिणाम का प्रकार जानते हैं, तो ये ऐसे कार्य हैं जो स्थिर होते हैं।

यदि हमें तर्कों के अर्थ को देखने की आवश्यकता है, तो ये स्थिर कार्य नहीं हैं।

जब कंपाइलर कोड का अनुकूलन कर सकता है, तो निष्पादन समय में अंतर परिमाण के दो आदेशों द्वारा प्राप्त किया जाता है। दूसरे उदाहरण में, यह केवल एक नए सरणी के लिए आवंटित किया गया था, एक युगल अधिक बाइट्स और कुछ भी नहीं। यह विकल्प पिछले वाले की तुलना में बहुत अधिक प्रभावी है।

जब हम जूलिया में कोड लिखते हैं, तो यह देखना मुख्य बात है। अगर आप पाइथन की तरह लिखते हैं, तो यह पाइथन की तरह काम करेगा। यदि आप NumPy पर समान संचालन करते हैं, तो एक बिंदु के साथ या बिना शून्य एक भूमिका नहीं निभाता है। लेकिन जूलिया में, यह प्रदर्शन को बहुत कम कर सकता है।

सौभाग्य से, यह पता लगाने की एक विधि है कि क्या कोई समस्या मौजूद है। यह @code_warntype मैक्रो है, जो आपको यह पता लगाने की अनुमति देता है कि क्या कंपाइलर अनुमान लगा सकता है कि कौन से प्रकार हैं और यदि सबकुछ ठीक है तो ऑप्टिमाइज़ करें।



पहले विकल्प (बाएं) में, कंपाइलर प्रकार के बारे में निश्चित नहीं है और इसे लाल रंग में प्रदर्शित करता है। दूसरे मामले में, इस तरह के तर्क के लिए हमेशा Float64 होगा, ताकि आप कोड को बहुत कम उत्पन्न कर सकें।

यह अभी तक एलएलवीएम नहीं है, लेकिन लेबल किए गए जूलिया कोड, return 0 या return 0.0 में परिमाण के दो आदेशों का प्रदर्शन अंतर है।

metaprogramming

मेटाप्रोग्रामिंग वह है जब हम किसी प्रोग्राम में प्रोग्राम बनाते हैं और उन्हें चलते-फिरते चलाते हैं।

यह एक शक्तिशाली तरीका है जो आपको कई अलग-अलग दिलचस्प चीजें करने की अनुमति देता है। एक क्लासिक उदाहरण Django ORM है, जो मेटाक्लासेस का उपयोग करके फ़ील्ड बनाता है।

कई लोग टिम पीटर के लेखक, पिथॉन के लेखक के अस्वीकरण को जानते हैं: “मेटाक्लस एक गहरा जादू है, जिसे 99% उपयोगकर्ताओं को कभी भी चिंता नहीं करनी चाहिए। यदि आप सोच रहे हैं कि पायथन में मेटाक्लास की आवश्यकता है, तो आपको उनकी आवश्यकता नहीं है। यदि आपको उनकी आवश्यकता है, तो आप वास्तव में जानते हैं कि उनका उपयोग क्यों और कैसे किया जाए। ”

मेटाप्रोग्रामिंग के साथ, स्थिति समान है, लेकिन जूलिया में यह बहुत गहरा है, यह पूरी भाषा की एक महत्वपूर्ण विशेषता है। जूलिया कोड किसी भी अन्य के समान डेटा संरचना है, आप हेरफेर कर सकते हैं, जोड़ सकते हैं, अभिव्यक्ति बना सकते हैं, और यह सब काम करेगा।

 julia> x = 4; julia> typeof(:(x+1)) Expr julia> expr = :(x+1) :(x + 1) julia> expr.head :call julia> expr.args 3-element Array{Any,1}: :+ :x 1 

मैक्रोज़ जूलिया में मेटाप्रोग्रामिंग टूल्स में से एक हैं : हम उन्हें कुछ देते हैं, वे देखते हैं, सही जोड़ते हैं, अनावश्यक हटाते हैं, और परिणाम देते हैं। पिछले सभी उदाहरणों में, हमने फ़ंक्शन को कॉल पास किया, और मैक्रो ने कॉल को पार्स किया। यह सब सिंटेक्स ट्री के साथ काम करने के स्तर पर होता है।

आप बहुत ही सरल भावों को पार्स कर सकते हैं: यदि यह है, उदाहरण के लिए, (x+1) , तो यह + फ़ंक्शन के लिए एक कॉल है (इसके अलावा एक ऑपरेटर नहीं है, जैसा कि कई अन्य भाषाओं में है, लेकिन एक फ़ंक्शन) और दो तर्क: एक चरित्र (एक कोलोन का अर्थ है कि यह एक चरित्र है ), और दूसरा सिर्फ एक स्थिर है।

एक और सरल मैक्रो उदाहरण:

 macro named(name, expr) println("Starting $name") return quote $(esc(expr)) end end julia> @named "some process" x=5; Starting some process julia> x 5 

उदाहरण के लिए, मैक्रोज़ का उपयोग करते हुए, डेटा फ़्रेम के लिए प्रगति संकेतक या फ़िल्टर बनाए जाते हैं - यह जूलिया में एक सामान्य तंत्र है।

मैक्रोज़ को कॉल के समय निष्पादित नहीं किया जाता है, लेकिन कोड को पार्स करते समय।

जूलिया में यह मुख्य मैक्रो फीचर है। - , . , , .

,

Julia — . .

• Julia . .
• , . , , C .
• Julia JIT- . , , , , .
• — . .
• ( ). , . , , .
• Julia — .

पारिस्थितिकी तंत्र

, , Julia . , , data science , , , Python. , Python Pandas, , , , Julia .

Julia , Python 2008 . Python, , Julia. , . , Julia.

( ) Python Julia

. Julia: , , .…

. .

• DataFrames.jl .
• JuliaDB , .
• Query.jl . Pandas — - , ..

Plotting . Matplotlib , Julia. : VegaLite.jl , Plots.jl , , Gadfly.jl .

. TensorFlow , Flux.jl. Flux , , , Keras TensorFlow, . .

Scikit-learn . , , sklearn, , .

XGBoost . , Julia .

?

Jupyter . IDE — Juno, Visual Studio, .

. GPU/TPU . CUDAnative.jl Julia . Julia-, - , . , , , , .

: C, Fortran, Python .

, .

Packaging : Julia: , , ..

, , . , , . , PyTorch , TensorFlow, , .

, , , . Julia, , , . , , Zygote.jl . Flux.jl.

 julia> using Zygote julia> φ(x) = x*sin(x) julia> Zygote.gradient(φ, π/2.) (1.0,) julia> model = Chain(Dense(768, 128, relu), Dense(128, 10), softmax) julia> loss(x, y) = crossentropy(model(x), y) + sum(norm, params(model)) julia> optimizer = ADAM(0.001) julia> Flux.train!(loss, params(model), data, optimizer) julia> model = Chain(x -> sqrt(x), x->x-1) 

φ , , , .

Zygote «source-to-source»: , , . differentiable programming — — backpropagation , .

Julia : «source-to-source» , . , .

Julia ?

, — . .

- , , , — .

, , .

Julia , .

• , , . Julia «» .
• , API, , .

Moscow Python Conf++ , 27 , Python Julia. , , telegram- MoscowPython.