ऑप्टिमाइज़िंग कंपाइलर कैसे काम करता है

ऑप्टिमाइज़िंग कंपाइलर आधुनिक सॉफ़्टवेयर का आधार हैं: वे प्रोग्रामर को उनकी समझ में आने वाली भाषा में कोड लिखने की अनुमति देते हैं, फिर उसे कोड में परिवर्तित करते हैं जिसे कुशलता से उपकरण द्वारा निष्पादित किया जा सकता है। कंपाइलरों के अनुकूलन का कार्य यह समझना है कि आपने जो इनपुट प्रोग्राम लिखा है, वह आउटपुट प्रोग्राम बनाता है जो एक ही काम करता है, केवल तेजी से।

इस लेख में, हम संकलक को अनुकूलित करने में कुछ मूल अनुमान तकनीकों पर नज़र डालेंगे: एक ऐसे कार्यक्रम को कैसे डिज़ाइन किया जाए जिसके साथ संकलक आसानी से काम कर सके; आपके कार्यक्रम में क्या कटौती की जा सकती है और इसे कम करने और तेज करने के लिए उनका उपयोग कैसे किया जा सकता है।

प्रोग्राम ऑप्टिमाइज़र कहीं भी चला सकते हैं: एक बड़े संकलन प्रक्रिया ( स्काला ऑप्टिमाइज़र ) के हिस्से के रूप में; एक अलग कार्यक्रम के रूप में, संकलक के बाद और निष्पादन से पहले लॉन्च किया गया ( प्रोगार्ड ); या एक रनटाइम वातावरण के भाग के रूप में जो अपने निष्पादन ( JVM JIT संकलक ) के दौरान एक कार्यक्रम का अनुकूलन करता है। ऑप्टिमाइज़र के काम में सीमाएं स्थिति के आधार पर अलग-अलग होती हैं, लेकिन उनके पास एक काम है: इनपुट प्रोग्राम को लेना और इसे आउटपुट एक में बदलना, जो एक ही काम करता है, लेकिन तेजी से।

सबसे पहले, हम ड्राफ्ट प्रोग्राम के लिए अनुकूलन के कुछ उदाहरणों को देखेंगे, ताकि आप समझ सकें कि आमतौर पर ऑप्टिमाइज़र क्या करते हैं और इसे मैन्युअल रूप से कैसे करते हैं। फिर हम कार्यक्रमों को प्रस्तुत करने के कई तरीकों पर विचार करेंगे, और अंत में हम एल्गोरिदम और तकनीकों का विश्लेषण करेंगे जिनके साथ आप कार्यक्रमों का विश्लेषण कर सकते हैं और फिर उन्हें छोटा और तेज बना सकते हैं।

ड्राफ्ट कार्यक्रम

सभी उदाहरण जावा में दिए जाएंगे। यह भाषा बहुत सामान्य है और एक अपेक्षाकृत सरल कोडांतरक - जावा बाइटकोड में संकलित है । इसलिए हम एक अच्छी नींव बनाएंगे, जिसकी बदौलत हम वास्तविक, निष्पादन योग्य उदाहरणों का उपयोग करके संकलन अनुकूलन तकनीकों का पता लगा सकते हैं। नीचे वर्णित सभी तकनीक लगभग सभी अन्य प्रोग्रामिंग भाषाओं में लागू हैं।

सबसे पहले, एक मसौदा कार्यक्रम पर विचार करें। इसमें विभिन्न तर्क शामिल हैं, प्रक्रिया के अंदर मानक परिणाम को पंजीकृत करता है और गणना किए गए परिणाम को वापस करता है। कार्यक्रम खुद ही समझ में नहीं आता है, लेकिन मौजूदा व्यवहार को बनाए रखते हुए क्या अनुकूलित किया जा सकता है, इसका चित्रण के रूप में उपयोग किया जाएगा:

static int main(int n){ int count = 0, total = 0, multiplied = 0; Logger logger = new PrintLogger(); while(count < n){ count += 1; multiplied *= count; if (multiplied < 100) logger.log(count); total += ackermann(2, 2); total += ackermann(multiplied, n); int d1 = ackermann(n, 1); total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; } // https://en.wikipedia.org/wiki/Ackermann_function static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } interface Logger{ public Logger log(Object a); } static class PrintLogger implements Logger{ public PrintLogger log(Object a){ System.out.println(a); return this; } } static class ErrLogger implements Logger{ public ErrLogger log(Object a){ System.err.println(a); return this; } } 

अभी के लिए, हम यह मानते हैं कि यह कार्यक्रम वह सब है जो हमारे पास है, कोड का कोई अन्य भाग इसे नहीं कहता है। यह main डेटा में प्रवेश करता है, निष्पादित करता है और परिणाम देता है। अब इस प्रोग्राम को ऑप्टिमाइज़ करते हैं।

अनुकूलन के उदाहरण

कास्टिंग और इनलाइनिंग टाइप करें

आपने देखा होगा कि logger चर का एक गलत प्रकार है: Logger लेबल के बावजूद, कोड के आधार पर, हम यह निष्कर्ष निकाल सकते हैं कि यह एक विशिष्ट उपवर्ग है - PrintLogger :

 - Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger(); 

अब हम जानते हैं कि logger PrintLogger , और हम जानते हैं कि logger.log को कॉल करने पर एक ही कार्यान्वयन हो सकता है। आप इनलाइन कर सकते हैं:

 - if (multiplied < 100) logger.logcount(); + if (multiplied < 100) System.out.println(count); 

यह अनावश्यक ErrLogger वर्ग का उपयोग करके कार्यक्रम को कम करेगा, साथ ही साथ विभिन्न public Logger log तरीकों को हटाकर, क्योंकि हम कॉल के एक ही स्थान पर इनलाइन करते हैं।

जमावट कांस्टेंट

कार्यक्रम के निष्पादन के दौरान, count और total परिवर्तन, लेकिन multiplied नहीं होता है: यह 0 से शुरू होता है और हर बार multiplied = multiplied * count माध्यम से multiplied = multiplied * count , 0 बराबर रहता है। तो, आप इसे पूरे कार्यक्रम में 0 बदल सकते हैं:

 static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; } 

परिणामस्वरूप, हम देखते हैं कि d1 * multiplied हमेशा 0 , जिसका अर्थ है कि total += d1 * multiplied कुछ भी नहीं करता है और इसे हटाया जा सकता है:

 - total += d1 * multiplied 

मृत कोड हटाना

multiplied और यह महसूस करने के बाद कि total += d1 * multiplied कुछ नहीं करता है, आप int d1 की परिभाषा को हटा सकते हैं:

 - int d1 = ackermann(n, 1); 

यह अब कार्यक्रम का हिस्सा नहीं है, और चूंकि ackermann एक शुद्ध कार्य है, इसलिए स्थापना रद्द करने से कार्यक्रम का परिणाम प्रभावित नहीं होगा।

इसी तरह, logger.log बाद, logger खुद का उपयोग नहीं करता है और उसे हटाया जा सकता है:

 - PrintLogger logger = new PrintLogger(); 

शाखा निकालना

अब हमारे चक्र में पहला सशर्त संक्रमण 0 < 100 पर निर्भर करता है। चूंकि यह हमेशा सच होता है, आप बस शर्त को हटा सकते हैं:

 - if (0 < 100) System.out.println(count); + System.out.println(count); 

कोई भी सशर्त संक्रमण जो हमेशा सच होता है, हालत के शरीर में इनलाइन हो सकता है, और ऐसे संक्रमणों के लिए जो हमेशा गलत होते हैं, आप इसके शरीर के साथ-साथ स्थिति को हटा सकते हैं।

आंशिक गणना

अब हम तीन शेष कॉल का विश्लेषण करते हैं:

  total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count); 

• पहले के दो निरंतर तर्क हैं। फ़ंक्शन शुद्ध है, और प्रारंभिक गणना पर ackermann(2, 2) 7. बराबर होना चाहिए 7.
• दूसरी कॉल में एक निरंतर तर्क 0 और एक अज्ञात n । आप इसे ackermann की परिभाषा में पास कर सकते हैं, और यह पता चला है कि जब m 0 , तो फ़ंक्शन हमेशा n + 1.
  
• तीसरी कॉल में, दोनों तर्क अज्ञात हैं: n और count । चलो उन्हें अभी के लिए जगह में छोड़ दें।
  

यह देखते हुए कि ackermann लिए कॉल इस प्रकार परिभाषित किया गया है:

 static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } 

आप इसे सरल कर सकते हैं:

 - total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count); 

देर से शेड्यूल करना

डी 2 की परिभाषा का उपयोग केवल सशर्त if (count % 2 == 0) में किया जाता है if (count % 2 == 0) । चूँकि ackermann गणना साफ है, आप इस कॉल को एक सशर्त ackermann स्थानांतरित कर सकते हैं ताकि इसका उपयोग होने तक संसाधित न हो:

 - int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + } 

यह ackermann(n, count) आधे कॉल से बच जाएगा, जिससे प्रोग्राम निष्पादन में तेजी ackermann(n, count) ।

तुलना के लिए, System.out.println फ़ंक्शन साफ ​​नहीं है, जिसका अर्थ है कि यह कार्यक्रम के शब्दार्थ को बदलने के बिना सशर्त छलांग के अंदर या बाहर स्थानांतरित नहीं किया जा सकता है।

अनुकूलित परिणाम

सभी अनुकूलन प्राप्त करने के बाद, हमें निम्नलिखित स्रोत कोड प्राप्त होते हैं:

 static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } 

हालाँकि हमने मैन्युअल रूप से अनुकूलित किया है, यह सब अपने आप हो सकता है। जेवीएम कार्यक्रमों के लिए मैंने जो प्रोटोटाइप ऑप्टिमाइज़र लिखा था, उसका विघटित परिणाम निम्नलिखित है:

 static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {} 

विघटित कोड मैन्युअल रूप से अनुकूलित संस्करण से थोड़ा अलग है। कुछ कंपाइलर अनुकूलन नहीं कर सकता (उदाहरण के लिए, new PrintLogger लिए एक अप्रयुक्त कॉल), लेकिन कुछ अलग तरीके से किया गया था (उदाहरण के लिए, ackermann और ackermann__I__TI1__I )। लेकिन बाकी के लिए, ऑटोमैटिक ऑप्टिमाइज़र ने मेरे द्वारा किए गए तर्क का उपयोग करते हुए, जैसा किया था, वैसा ही किया।

सवाल उठता है: कैसे?

मध्यवर्ती विचार

यदि आप अपना स्वयं का ऑप्टिमाइज़र बनाने की कोशिश करते हैं, तो पहला सवाल जो शायद उठता है, वह शायद सबसे महत्वपूर्ण होगा: "प्रोग्राम" क्या है?

निस्संदेह, आप स्रोत कोड के रूप में प्रोग्राम लिखने और बदलने के लिए उपयोग किए जाते हैं। आपने निश्चित रूप से संकलित बायनेरिज़ के रूप में उन्हें निष्पादित किया, शायद बायनेरिज़ को भी डीबग किया। आप एक वाक्यविन्यास वृक्ष , तीन-पता कोड , ए-सामान्य , निरंतर पासिंग स्टाइल, या एकल स्टेटिक असाइनमेंट के रूप में कार्यक्रमों में आ सकते हैं।

कार्यक्रमों के विभिन्न अभ्यावेदन का एक पूरा चिड़ियाघर है। यहाँ हम अनुकूलक के अंदर एक "कार्यक्रम" का प्रतिनिधित्व करने के सबसे महत्वपूर्ण तरीकों पर चर्चा करेंगे।

स्रोत कोड

 static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } 

असम्बद्ध स्रोत कोड भी आपके कार्यक्रम का एक प्रतिनिधित्व है। यह अपेक्षाकृत कॉम्पैक्ट है, मानव-पठनीय है, लेकिन इसकी दो कमियां हैं:

• स्रोत कोड में नाम और स्वरूपण के सभी विवरण शामिल हैं, जो प्रोग्रामर के लिए महत्वपूर्ण हैं, लेकिन कंप्यूटर के लिए बेकार हैं।
  
• सही लोगों की तुलना में स्रोत कोड के रूप में कई और गलत कार्यक्रम हैं, और अनुकूलन के दौरान, आपको यह सुनिश्चित करने की आवश्यकता है कि आपका प्रोग्राम सही इनपुट स्रोत कोड से सही आउटपुट स्रोत कोड में परिवर्तित हो।
  

ये कारक अनुकूलनकर्ता के लिए स्रोत कोड के रूप में कार्यक्रम के साथ काम करना मुश्किल बनाते हैं। हां, आप इस तरह के कार्यक्रम को परिवर्तित कर सकते हैं , उदाहरण के लिए, पैटर्न को पहचानने और बदलने के लिए नियमित अभिव्यक्तियों का उपयोग करना । हालांकि, दो कारकों में से पहला, विस्तृत विवरणों की एक बहुतायत के साथ पैटर्न को मज़बूती से पहचानना मुश्किल बनाता है। और दूसरा कारक भ्रमित होने और गलत परिणामी कार्यक्रम प्राप्त करने की संभावना को बहुत बढ़ाता है।

ये प्रतिबंध कार्यक्रम के कन्वर्टर्स के लिए स्वीकार्य हैं, जिन्हें मानव पर्यवेक्षण के तहत निष्पादित किया जाता है, उदाहरण के लिए, जब आप कोड बेस को रिफ्लेक्टर और कोड बेस को बदलने के लिए उपयोग कर सकते हैं। हालाँकि, आप किसी स्वचालित ऑप्टिमाइज़र के प्राथमिक मॉडल के रूप में स्रोत कोड का उपयोग नहीं कर सकते।

सार सिंटेक्स के पेड़

 static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) ) 

सार सिंटेक्स ट्री (एएसटी) एक और सामान्य मध्यवर्ती प्रारूप है। वे स्रोत कोड की तुलना में अमूर्त सीढ़ी के अगले चरण पर स्थित हैं। आमतौर पर, एएसटी सभी स्रोत कोड फ़ॉर्मेटिंग, इंडेंटेशन और टिप्पणियों को छोड़ देता है, लेकिन उन स्थानीय चरों के नामों को बरकरार रखता है जिन्हें अधिक सार निरूपण में छोड़ दिया जाता है।

स्रोत कोड की तरह, एएसटी अनावश्यक जानकारी को एन्कोड करने की संभावना से ग्रस्त है जो कार्यक्रम के वास्तविक शब्दार्थ को प्रभावित नहीं करता है। उदाहरण के लिए, निम्नलिखित दो कोड टुकड़े शब्दार्थ समान हैं; वे केवल स्थानीय चर के नाम में भिन्न होते हैं, लेकिन फिर भी अलग-अलग एएसटी होते हैं:

 static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) ) 

मुख्य बिंदु यह है कि यद्यपि एएसटीएस में एक पेड़ की संरचना होती है, लेकिन उनमें नोड्स होते हैं जो पेड़ों की तरह शब्दार्थ का व्यवहार करते हैं: Ident("r") और Ident("s") के मान उनके उपप्रकार की सामग्री से नहीं, बल्कि अपस्ट्रीम Assign("r", ...) नोड Ident("s") निर्धारित Ident("s") हैं। Assign("r", ...) और Assign("s", ...) । वास्तव में, Ident और Assign बीच अतिरिक्त अर्थ संबंध हैं जो एएसटी ट्री संरचना में किनारों के समान महत्वपूर्ण हैं:



ये कनेक्शन कार्यों के पुनरावर्ती परिभाषाओं की उपस्थिति में चक्र सहित एक सामान्यीकृत ग्राफ संरचना बनाते हैं।

बाईटकोड

चूंकि हमने जावा को मुख्य भाषा के रूप में चुना है, इसलिए संकलित कार्यक्रमों को .class फ़ाइलों में Java bytecode के रूप में सहेजा जाता है।

हमारे ackermann फ़ंक्शन को याद करें:

 static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } 

यह इस बाइटकोड को संकलित करता है:

  0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn 

जावा वर्चुअल मशीन (JVM), जो जावा बाइटकोड को चलाता है, एक स्टैक और रजिस्टरों के संयोजन के साथ एक मशीन है: इसमें ऑपरेंड्स (STACK) का एक स्टैक होता है जिसमें मानों को जोड़-तोड़ किया जाता है, और स्थानीय चर (LOCALS) की एक सरणी जिसमें ये मान संग्रहीत किए जा सकते हैं। फ़ंक्शन स्थानीय वेरिएबल्स के पहले एन स्लॉट्स में एन मापदंडों के साथ शुरू होता है। जैसा कि यह निष्पादित करता है, फ़ंक्शन स्टैक पर डेटा को स्थानांतरित करता है, उन पर संचालित होता है, उन्हें वापस चर में डालता है, कॉल को ऑपेरैंड स्टैक से मूल्य return करने के लिए वापस बुलाता है।

यदि आप स्टैक और स्थानीय चर तालिका के बीच चलने वाले मानों का प्रतिनिधित्व करने के लिए ऊपर दिए गए बाईटेकोड को एनोटेट करते हैं, तो यह इस तरह दिखेगा:

  BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| | 

यहां, a0 और a1 का उपयोग करते हुए a1 फ़ंक्शन तर्क प्रस्तुत किए, जो फ़ंक्शन के आरंभ में LOCALS तालिका में संग्रहीत हैं। 1 iconst_1 माध्यम से लोड किए गए स्थिरांक का प्रतिनिधित्व करता है, और v1 से v7 , मध्यवर्ती मूल्यों की गणना करता है। v1 , v3 और v7 लौटाने के लिए तीन ireturn निर्देश हैं। यह फ़ंक्शन अन्य स्थानीय चर को परिभाषित नहीं करता है, इसलिए LOCALS सरणी केवल इनपुट तर्कों को संग्रहीत करती है।

ऊपर, हमने अपने फ़ंक्शन के दो वेरिएंट देखे - ackermannA और ackermannB । इसलिए वे बाइटकोड में दिखते हैं:

  BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| | 

चूंकि स्रोत कोड दो तर्कों को लेता है और उन्हें स्थानीय चर में डालता है, बायोटेक में LOCAL सूचकांकों 0 और 1 से तर्क मानों को लोड करने और उन्हें सूचकांकों 2 और 3 के तहत सहेजने के लिए समान निर्देश हैं। हालाँकि, bytecode आपके स्थानीय चर के नामों में दिलचस्पी नहीं रखता है: यह इसके साथ काम करता है। उनके द्वारा विशेष रूप से LOCALS सरणी में अनुक्रमित के साथ। इसलिए, ackermannA और ackermannB समान ackermannB होंगे। यह तर्कसंगत है, क्योंकि वे शब्दार्थ के समकक्ष हैं!

हालाँकि, ackermannA और ackermannB को मूल ackermann रूप में एक ही ackermannB में संकलित नहीं किया जाता है: हालाँकि, bytecode को स्थानीय चरों के नाम से अलग किया गया है, फिर भी यह इन चरों से लोडिंग / सेविंग के लिए पूरी तरह से अमूर्त नहीं है। यह अभी भी हमारे लिए महत्वपूर्ण है कि मान LOCALS और STACK के साथ कैसे चलते हैं, हालांकि वे कार्यक्रम के वास्तविक व्यवहार को प्रभावित नहीं करते हैं।

लोडिंग / सेविंग से अमूर्तता की कमी के अलावा, बायोटेक में एक और खामी है: अधिकांश रैखिक असेंबलरों की तरह, यह कॉम्पैक्टनेस के संदर्भ में बहुत अनुकूलित है, और अनुकूलन के लिए इसे संशोधित करना बहुत मुश्किल हो सकता है।

इसे स्पष्ट करने के लिए, आइए मूल ackermann फ़ंक्शन के बाइटकोड को देखें:

  BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| | 

चलो एक मोटा बदलाव करें: फ़ंक्शन को 30: invokestatic ackermann:(II)I कॉल करें 30: invokestatic ackermann:(II)I इसके पहले तर्क का उपयोग नहीं करता 30: invokestatic ackermann:(II)I । और फिर इस कॉल को समकक्ष कॉल 30: invokestatic ackermann2:(I)I बदला जा सकता है, जो केवल एक तर्क लेता है। यह एक सामान्य अनुकूलन है, जो पहले तर्क 30: invokestatic ackermann:(II)I गणना करने के लिए इस्तेमाल किए गए किसी भी कोड को बाहर निकालने के लिए "मृत कोड हटाने" का उपयोग करने की अनुमति देता है 30: invokestatic ackermann:(II)I

ऐसा करने के लिए, हमें न केवल निर्देश 30 को बदलने की जरूरत है, बल्कि निर्देशों की सूची को भी देखना होगा और यह समझना होगा कि पहले तर्क की गणना कहां की गई है ( v4 में v4 ), और इसे हटा भी दें। हम 30 से 22 , और 22 से 21 और 20 से निर्देश से लौटते हैं। अंतिम संस्करण:

  BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| | 

हम अभी भी एक साधारण ackermann फ़ंक्शन के लिए इस तरह के एक साधारण बदलाव कर सकते हैं। लेकिन वास्तविक परियोजनाओं में उपयोग किए जाने वाले बड़े कार्यों में, कई, परस्पर परिवर्तन करना अधिक कठिन होगा। सामान्य तौर पर, आपके कार्यक्रम में किसी भी छोटे अर्थ परिवर्तन से पूरे बायोटेक में कई बदलावों की आवश्यकता हो सकती है।

आप देख सकते हैं कि हमने LOCALS और STACK में मूल्यों का विश्लेषण करके ऊपर वर्णित परिवर्तन किया है: हमने देखा कि v4 निर्देश 22 से निर्देश 30 तक कैसे पारित किया जाता है, और 22 a0 और 1 डेटा लेता है, जो निर्देश 21 और 20 से आते हैं। इन मूल्यों को ग्राफ के सिद्धांत के अनुसार LOCALS और STACK के बीच स्थानांतरित किया जाता है: मूल्य की गणना करने वाले निर्देश से इसके आगे के उपयोग के स्थान पर।

हमारे एएसटीएस में Ident / Assign जोड़े की तरह, LOCALS और STACK के बीच पारित होने वाले मान मूल्यों की गणना और उनके उपयोग के बिंदुओं के बीच एक ग्राफ बनाते हैं। तो हम सीधे ग्राफ़ के साथ काम क्यों नहीं शुरू करते?

डेटा प्रवाह रेखांकन

डेटा प्रवाह रेखांकन बायटेकोड के बाद अमूर्तता का अगला स्तर है। यदि हम Ident / Assign संबंधों के साथ अपने वाक्यविन्यास के पेड़ का विस्तार करते हैं, या यदि हम यह पता लगाते हैं कि कैसे बायटेकोड LOCALS और STACK के बीच मूल्यों को स्थानांतरित करता है, तो हम एक ग्राफ बना सकते हैं। ackermann समारोह के लिए ackermann यह इस तरह दिखता है:



एएसटी या जावा स्टैक-बायटेकोड बायटेकोड के विपरीत, डेटा प्रवाह ग्राफ़ एक "स्थानीय चर" की अवधारणा का उपयोग नहीं करते हैं: इसके बजाय, ग्राफ़ में प्रत्येक मूल्य और इसके उपयोग के स्थान के बीच सीधे लिंक होते हैं। जब बायटेकोड का विश्लेषण करते हैं, तो यह समझने के लिए अक्सर आवश्यक होता है कि मान कैसे चलते हैं; एएसटी विश्लेषण में पेड़ को ट्रैक करना और Assign / Ident संघों के प्रतीक तालिका के साथ काम करना शामिल है; और डेटा प्रवाह रेखांकन का विश्लेषण अक्सर बदलावों का एक सीधा ट्रैकिंग है - एक कार्यक्रम पेश करने के पतियों के बिना "चलती मूल्यों" का शुद्ध विचार।

रेखीय बाइटकोड की तुलना में ackermann हेरफेर करना भी आसान होता है: ackermann कॉल के साथ एक नोड को ackermann कॉल के साथ ackermann और एक तर्क को ackermann बस ग्राफ़ नोड (हरे रंग में चिह्नित) को बदल रहा है और ट्रांजिट नोड्स (लाल रंग में चिह्नित) के साथ एक इनपुट लिंक को हटा रहा है:



जैसा कि आप देख सकते हैं, ackermann(int n, int m) साथ प्रोग्राम ( ackermann(int n, int m) जगह) में एक छोटा सा बदलाव डेटा स्ट्रीम ग्राफ में अपेक्षाकृत स्थानीय परिवर्तन में बदल जाता है।

सामान्य तौर पर, रेखीय बाइटकोड या एएसटी के साथ रेखांकन के साथ काम करना बहुत आसान होता है: वे विश्लेषण करना और बदलना आसान होते हैं।

ग्राफ़ के इस विवरण में बहुत सारे विवरण नहीं हैं: ग्राफ़ के वास्तविक भौतिक प्रतिनिधित्व के अलावा, राज्य और प्रवाह नियंत्रण के मॉडलिंग के कई अन्य तरीके हैं, जो लेख के दायरे के साथ और उससे परे काम करना अधिक कठिन हैं। मैंने ग्राफ़ बदलने के बारे में कई विवरणों को छोड़ दिया है, उदाहरण के लिए, लिंक जोड़ना और निकालना, आगे और रिवर्स संक्रमण, क्षैतिज और ऊर्ध्वाधर संक्रमण (चौड़ाई और गहराई में), आदि। यदि आपने एल्गोरिदम का अध्ययन किया है, तो यह सब आपको परिचित होना चाहिए। ।

अंत में, हमने रैखिक बायोटेक से ग्राफ के लिए रूपांतरण एल्गोरिदम को छोड़ दिया, और फिर ग्राफ से वापस बायटेकोड तक। यह अपने आप में एक दिलचस्प काम है, लेकिन हम इसे स्वतंत्र अध्ययन के लिए छोड़ देते हैं।

के विश्लेषण

कार्यक्रम का विचार प्राप्त करने के बाद, हमें इसका विश्लेषण करने की आवश्यकता है: कुछ तथ्यों का पता लगाएं जो आपको कार्यक्रम को उसके व्यवहार को बदलने के बिना बदलने की अनुमति देंगे। ऊपर चर्चा की गई कई अनुकूलन कार्यक्रम के विश्लेषण पर आधारित हैं:

• लगातार तह: क्या अभिव्यक्ति का परिणाम एक ज्ञात निरंतर मूल्य काम कर रहा है? क्या अभिव्यक्ति की गणना शुद्ध है?
  
• टाइप कास्टिंग और इनलाइनिंग: एक विधि कॉल प्रकार है जिसे कॉल विधि के एकल कार्यान्वयन के साथ टाइप किया जाता है?
  
• : ?
  
• : «»? - ? ?
  
• : , ?
  

, , , . , , , .

, , , — , . .

(Inference Lattice)

, . , «» - :

• Integer ? String ? Array[Float] ? PrintLogger ?
  
• CharSequence ? String , - StringBuilder ?
  
• Any , , ?
  

:



: , "hello" String , String CharSequence . "hello" , (Singleton Type) — . :



, , . , . , , , String StringBuilder , , : CharSequence . , 0 , 1 , 2 , , Integer .



, , :



, , . , .

count

main :

 static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; } 

ackermann , count , multiplied logger . :



, count 0 block0 . block1 , , count < n : , block3 return , block2 , count 1 count , block1 . , < false , block3 .

?

• block0 . , count = 0.
  
• block1 , , n ( , Integer ), , if . block2 block3.
• block3 , , block1b , block2 , , block1c . , block2 count , 1 count.
• , count 0 1 : count Integer.
• : block1 n count Integer .
  
• block2 , count Integer + 1 -> Integer . , count Integer , .
  

multiplied

, multiplied :

• block0 . , multiplied 0.
  
• block1 , , . block2 block3 ( ).
  
• block2 , block2 ( 0 ) count ( Integer ). 0 * Integer -> 0 , multiplied 0.
  
• block1 block2 . multiplied 0 , .
  

multiplied 0 , , :

• multiplied < 100 true.
  
• if (multiplied < 100) logger.log(count); logger.log(count) .
  
• , multiplied , , 0 .
  

:



:



:

 static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; } 

, , , , .

multiplied -> 0 , , . , , . , .

, . :

• .
  
• .
  
• .
  
• : .
  

count , multiplied . , multiplied count , count multiplied . , .

, — : , . , ( ) . .

while , , O( ) . (, ) , , .

, .

, . , , , , .

. :

 static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; } 

:



main :

• main(n)
  
  • called(n, 0)
    
    • x * y x = n y = 0
    • n * 0 0
  • called(n, 0) 0
• main(n) 0
  

, , . .

, called(n, 0) 0 , :



:

 static int main(int n){ return 0; } 

: A B, C, D, D C, B, D A. A B B A, A A, , !

, Java:

 public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } } 

n int , Any : . , factorial int ( Integer ). factorial , factorial factorial , ! ?

Bottom

Bottom :



« , , ». Bottom factorial :

• block0 . n Integer , 1 1 , n == 1 , true false .
  
• true : return 1 .
  
• false n - 1 n Integer .
  
• factorial — , Bottom .
  
• * n: Integer factorial : Bottom Bottom .
  
• return Bottom .
• factorial 1 Bottom , 1 .
  
• 1 factorial , Bottom .
  
• Integer * 1 Integer .
  
• return Integer .
• factorial Integer 1 , Integer .
  
• factorial , Integer . * n: Integer factorial: Integer , Integer , .
  

factorial Integer , , .

, . Bottom , , .

* :

1. (n: Integer) * (factorial: Bottom)
   
2. (n: Integer) * (factorial: 1)
   
3. (n: Integer) * (factorial: Integer)
   

multiplied , O( ) . , , .

— , « ». , (« »), , (« »). .

main :

 static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; } 

, if (multiplied > 100) multiplied *= count multiplied *= 2 . .

, :

• multiplied > 100 true , count += 1 («»).
  
• total , («»).
  

, :

 static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; } 

, .

:



, , : block0 , block1 , , block1b , , block1c , , return block3 .

, multiplied -> 0 , :



:



, block1b ( 0 > 100 ) true . false block1c ( if ):



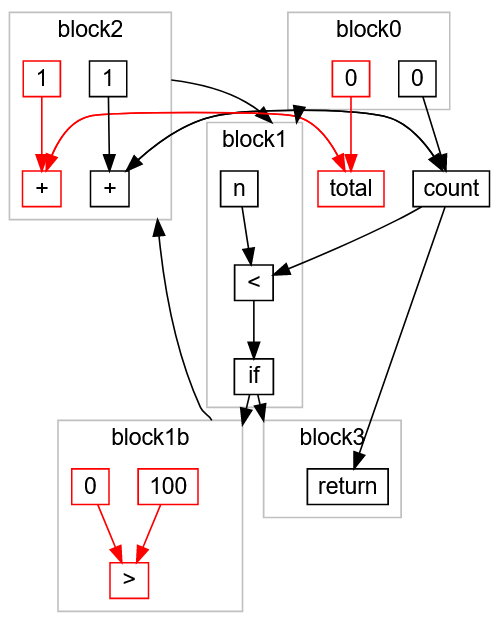
, « » total > , - , , . , return , : > , 100 , 0 block1b , total , 0 , + 1 , total block0 block2 . :



«» :

 static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; } 

निष्कर्ष

:

• -.
  
• , .
  
• , . .
  
• : «» «» , , .
  
• : , .
  
• , .
  

, , .

, . . , :

• Engineering a Compiler by Keith D Cooper & Linda Torczon
  
• Combining Analyses, Combining Optimizations by Cliff Noel Click Jr.
  
• Advanced Compiler Design and Implementation by Steven Muchnick