मैं अपने व्याख्यान प्रकाशित करना जारी रखता हूं, जो मूल रूप से "डिजिटल भूविज्ञान" की विशेषता में अध्ययन करने वाले छात्रों के लिए है। यह हब पर चक्र से तीसरा प्रकाशन है, पहला लेख एक परिचयात्मक था, इसे पढ़ने की आवश्यकता नहीं है। हालांकि, इस लेख को समझने के लिए, समीकरणों के रैखिक प्रणालियों के लिए परिचय को पढ़ना आवश्यक है, भले ही आपको पता हो कि यह क्या है, क्योंकि मैं इस परिचय से उदाहरणों के लिए बहुत कुछ संदर्भित करूंगा।

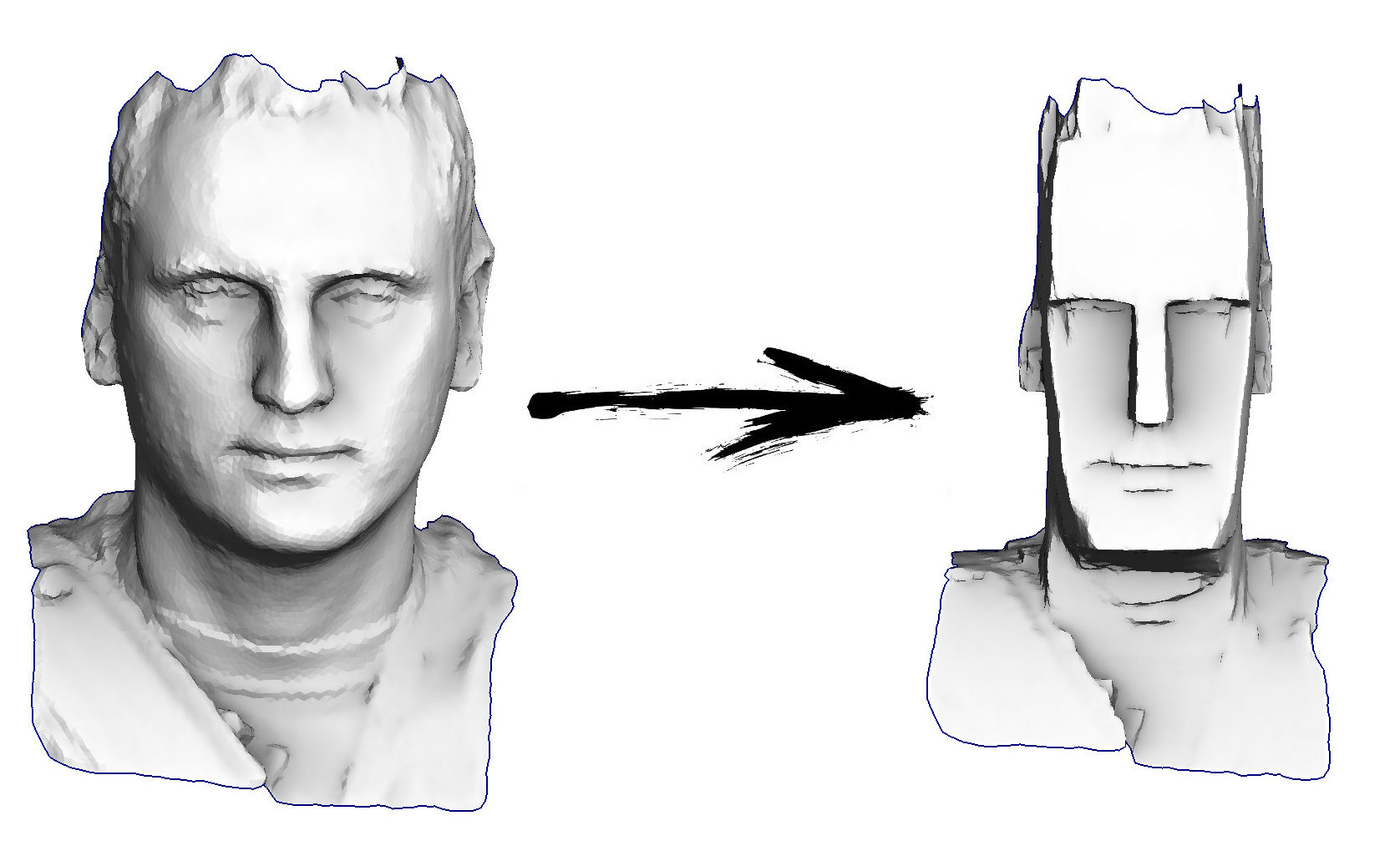
इसलिए, आज के लिए कार्य: ज्यामिति का सबसे सरल प्रसंस्करण सीखना, उदाहरण के लिए, ईस्टर द्वीप से मेरे सिर को एक मूर्ति में बदलने में सक्षम होना:



वर्तमान व्याख्यान योजना:

• संभाव्यता सिद्धांत पर शैक्षिक कार्यक्रम (परिचयात्मक लेख, वैकल्पिक)
  
• समीकरणों के रैखिक प्रणालियों का परिचय
  
• द्विघात रूपों का न्यूनतमकरण और ओएलएस समस्याओं के उदाहरण
  
• लेस्टर स्क्वेयर से लेकर न्यूरल नेटवर्क तक
  

आधिकारिक पाठ्यक्रम भंडार यहां रहता है । पुस्तक अभी समाप्त नहीं हुई है, मैं धीरे-धीरे हैबे पर प्रकाशित लेखों का संकलन कर रहा हूं।

इस लेख में, मेरा मुख्य उपकरण न्यूनतम द्विघात कार्यों को खोजना होगा; लेकिन इससे पहले कि हम इस उपकरण का उपयोग शुरू करें, आपको कम से कम यह समझने की जरूरत है कि उसके पास ऑन / ऑफ बटन कहां है। सबसे पहले, मेमोरी को रीफ्रेश करें और याद रखें कि मैट्रिसेस क्या हैं, एक पॉजिटिव नंबर क्या है और यह भी कि व्युत्पन्न क्या है।

मैट्रिक्स और संख्या

इस पाठ में मैं बहुतायत से मैट्रिक्स नोटेशन का उपयोग करूंगा, तो आइए याद करें कि यह क्या है। पाठ में आगे न देखें, कुछ सेकंड के लिए रुकें, और मैट्रिक्स बनाने की कोशिश करें।

विभिन्न मैट्रिक्स व्याख्याएं

जवाब बहुत आसान है। मैट्रिक्स सिर्फ एक कैबिनेट है जिसमें हॉर्सरैडिश संग्रहीत होता है। प्रत्येक गंदगी अपने सेल में निहित होती है, कोशिकाओं को पंक्तियों और स्तंभों में पंक्तिबद्ध किया जाता है। हमारे विशेष मामले में, सामान्य वास्तविक संख्याएं बकवास हैं; मैट्रिक्स प्रस्तुत करना प्रोग्रामर के लिए सबसे आसान है $$$ए$ कुछ पसंद है

float A[m][n]; 

ऐसे स्टोरेज की आवश्यकता क्यों है? वे क्या वर्णन करते हैं? शायद मैं आपको परेशान कर दूं, लेकिन मैट्रिक्स खुद कुछ भी नहीं बताता है, यह स्टोर करता है। उदाहरण के लिए, इसमें आप किसी भी कार्य के गुणांक को संग्रहीत कर सकते हैं। चलो एक दूसरे के लिए मेट्रिसेस के बारे में भूल जाएं, और कल्पना करें कि हमारे पास एक संख्या है $$$एक$ । इसका क्या मतलब है? हां, शैतान जानता है ... उदाहरण के लिए, यह एक फ़ंक्शन के अंदर गुणांक हो सकता है जो इनपुट के रूप में एक नंबर लेता है और आउटपुट के रूप में एक और देता है:

$$

$$f (x): \ mathbb R \ rightarrow \ mathbb R$$

एक गणितज्ञ इस तरह के एक फ़ंक्शन का एक संस्करण लिख सकता है

$$

$$च (x) = कुल्हाड़ी$$

ठीक है, प्रोग्रामर की दुनिया में, यह इस तरह दिखेगा:

 float f(float x) { return a*x; } 

दूसरी ओर, इस तरह के एक समारोह, और काफी अन्य क्यों नहीं? चलो एक और ले लो!

$$

$$f (x) = ax ^ 2$$

जब से मैंने प्रोग्रामर के बारे में शुरू किया, मुझे उसका कोड लिखना होगा :)

 float f(float x) { return x*a*x; } 

इन कार्यों में से एक रैखिक है, और दूसरा द्विघात है। कौन सा सही है? नहीं, संख्या ही $$$एक$ यह परिभाषित नहीं करता है, यह सिर्फ कुछ मूल्य संग्रहीत करता है! आपको किस फंक्शन की जरूरत है, एक जैसा निर्माण करें।

यही बात मैट्रिसेस के साथ भी होती है, इन स्टॉरेजों की जरूरत होती है जब एक ही नंबर (स्केलर) पर्याप्त संख्या में नहीं होते हैं, एक तरह का नंबर। मैट्रिस के ऊपर, नंबरों की तरह, जोड़ और गुणा के संचालन को परिभाषित किया गया है।

आइए कल्पना करें कि हमारे पास एक मैट्रिक्स है $$$ए$ उदाहरण के लिए, आकार 2x2:

$$

$$A = \ start {bmatrix} a_ {11} & a_ {12} \\ a_ {21} और a_ {22} \ end {bmatrix}$$

अपने आप में इस मैट्रिक्स का कोई मतलब नहीं है, उदाहरण के लिए, इसे एक फ़ंक्शन के रूप में व्याख्या किया जा सकता है

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2, \ quad f (x) = Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

यह फ़ंक्शन द्वि-आयामी वेक्टर को दो-आयामी वेक्टर में परिवर्तित करता है। आलेखीय रूप से, इसे छवि रूपांतरण के रूप में प्रस्तुत करना सुविधाजनक है: हम छवि को इनपुट के लिए देते हैं, और आउटपुट पर हमें इसका स्ट्रेच और / या घुमाया जाता है (संभवतः दर्पण भी!) संस्करण। बहुत जल्द मैं मैट्रिस की ऐसी व्याख्या के विभिन्न उदाहरणों के साथ एक तस्वीर दूंगा।

और मैट्रिक्स कर सकते हैं $$$ए$ एक फ़ंक्शन के रूप में कल्पना करें जो दो आयामी वेक्टर को एक स्केलर में परिवर्तित करता है:

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R, \ quad f (x) = x ^ \ top A x = \ sum \ limit_i \ sum \ limit_j a_ {ij} xi -i x_j$$

ध्यान दें कि घातांक वैक्टर के साथ बहुत परिभाषित नहीं है, इसलिए मैं लिख नहीं सकता $$$x ^ 2$ , जैसा कि उन्होंने साधारण संख्या के मामले में लिखा था। मैं उन लोगों के लिए अत्यधिक अनुशंसा करता हूं जो आसानी से मैट्रिक्स गुणन को टालने के लिए उपयोग नहीं किए जाते हैं, एक बार फिर मैट्रिक्स गुणन नियम को याद करते हैं, और अभिव्यक्ति को सत्यापित करते हैं। $$$x ^ \ top A x$ आम तौर पर अनुमति दी जाती है और वास्तव में बाहर निकलने पर एक स्केलर देता है। ऐसा करने के लिए, उदाहरण के लिए, आप स्पष्ट रूप से कोष्ठक डाल सकते हैं $$$x ^ \ top A x = (x ^ \ top A) x$ । मैं आपको याद दिलाता हूं कि हमारे पास है $$$x$ आयाम 2 का वेक्टर है (आयाम 2x1 के मैट्रिक्स में संग्रहीत), हम स्पष्ट रूप से सभी आयाम लिखते हैं:

$$

$$\ अंडरब्रेस {\ अंडरब्रेस {\ लेफ्ट (\ अंडरब्रेस {एक्स ^ \ टॉप} _ {1 \ टाइम्स 2} \ बार \ अंडरब्रेस {ए} _ {2 \ 2 बार 2} \ राइट)} _ {1 \ _ 2} 2} \ गुना \ अंडरब्रेस {x} _ {2 \ टाइम्स 1}} _ {1 \ टाइम्स 1}$$

प्रोग्रामर की गर्म और शराबी दुनिया में लौटते हुए, हम एक ही द्विघात फ़ंक्शन को कुछ इस तरह लिख सकते हैं:

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

पॉजिटिव नंबर क्या है?

अब मैं एक बहुत ही बेवकूफ सवाल पूछूंगा: एक सकारात्मक संख्या क्या है? हमारे पास अब एक विधेय नामक एक महान उपकरण है $$$>$ । लेकिन उस नंबर का जवाब देने के लिए अपना समय लें $$$एक$ सकारात्मक अगर और केवल अगर $$$a> 0$ यह बहुत आसान होगा। आइए सकारात्मकता को इस प्रकार परिभाषित करें:

परिभाषा १

संख्या $$$एक$ सकारात्मक और यदि केवल सभी गैर-वास्तविक के लिए $$$x \ in \ mathbb R, \ x \ neq 0$ हालत संतुष्ट है $$$कुल्हाड़ी ^ 2> 0$ ।

यह बहुत मुश्किल लग रहा है, लेकिन यह पूरी तरह से मैट्रीस पर लागू होता है:

परिभाषा २

वर्ग मैट्रिक्स $$$ए$ कहा जाता है सकारात्मक अगर, किसी भी गैर के लिए $$$x$ हालत संतुष्ट है $$$x ^ \ शीर्ष A x> 0$ अर्थात्, मूल को छोड़कर हर जगह समान द्विघात रूप सख्ती से सकारात्मक है।

मुझे सकारात्मकता की आवश्यकता क्यों है? जैसा कि मैंने लेख की शुरुआत में उल्लेख किया है, मेरा मुख्य उपकरण द्विघात कार्यों के न्यूनतम के लिए खोज करना होगा। लेकिन कम से कम खोज करने के लिए, यह अस्तित्व में होने पर बुरा नहीं होगा! उदाहरण के लिए, एक फ़ंक्शन $$$f (x) = - x ^ 2$ न्यूनतम स्पष्ट रूप से मौजूद नहीं है, क्योंकि नंबर -1 सकारात्मक नहीं है, और $$$च (x)$ वृद्धि के साथ अंतहीन घट जाती है $$$x$ : एक परवलय की शाखाएँ $$$च (x)$ नीचे देखो। सकारात्मक निश्चित मैट्रिक्स अच्छे हैं कि संबंधित द्विघात रूपों में एक पैराबोलाइड होता है जिसमें न्यूनतम (अद्वितीय) होता है। निम्नलिखित दृष्टांत मैट्रिस के सात अलग-अलग उदाहरणों को दर्शाता है। $$$2 बार 2$ , दोनों सकारात्मक निश्चित और सममित, और ऐसा नहीं है। ऊपरी पंक्ति: कार्यों के रूप में मेट्रिसेस की व्याख्या $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ । मध्य पंक्ति: कार्यों के रूप में मेट्रिसेस की व्याख्या $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R$ ।



इस प्रकार, मैं सकारात्मक निश्चित मैट्रिक्स के साथ काम करूंगा, जो सकारात्मक संख्याओं का एक सामान्यीकरण है। इसके अलावा, विशेष रूप से मेरे मामले में, मैट्रिसेस भी सममित होगा! यह उत्सुक है कि काफी बार जब लोग सकारात्मक निश्चितता के बारे में बात करते हैं, तो उनका मतलब समरूपता भी होता है, जिसे परोक्ष रूप से निम्नलिखित द्वारा समझाया जा सकता है (बाद के पाठ को समझने के लिए वैकल्पिक)।

द्विघात रूपों के मैट्रिक्स के समरूपता पर गेय विषयांतर

आइए द्विघात रूप को देखें $$$x ^ \ शीर्ष M x$ एक मनमाना मैट्रिक्स के लिए $$$एम$ ; इसके बाद $$$एम$ इसके ट्रांसपोज़ किए गए संस्करण का आधा हिस्सा तुरंत जोड़ें और घटाएँ:

$$

$$M = \ underbrace {\ frac {1} {2} (M + M ^ \ top)} _ {: = M_s} + \ underbrace {\ frac {1} {2} (MM ^ \ top)} {{ : = M_a} = M_s + M_a$$

मैट्रिक्स $$$M_s$ सममित: $$$M_s ^ \ top = M_s$ ; मैट्रिक्स $$$M_a$ antisymmetric: $$$M_a ^ \ top = -M_a$ । एक उल्लेखनीय तथ्य यह है कि किसी भी एंटीसिमेट्रिक मैट्रिक्स के लिए, संबंधित द्विघात रूप समान रूप से शून्य के बराबर है। यह निम्नलिखित अवलोकन से इस प्रकार है:

$$

$$q = x ^ \ शीर्ष M_a x = (x ^ \ शीर्ष M_a ^ \ शीर्ष x) ^ \ शीर्ष = - (x ^ \ शीर्ष M_a x) ^ \ शीर्ष = -q$$

वह है, द्विघात रूप $$$x ^ \ शीर्ष M_a x$ एक साथ बराबर $$$q$ और $$$-q$ , जो तभी संभव है $$$q \ equiv 0$ । इस तथ्य से यह इस प्रकार है कि एक मनमाना मैट्रिक्स के लिए $$$एम$ इसी चतुर्भुज रूप $$$x ^ \ शीर्ष M x$ एक सममित मैट्रिक्स के माध्यम से व्यक्त किया जा सकता है $$$M_s$ :

$$

$$x ^ \ शीर्ष M x = x ^ \ शीर्ष (M_s + M_a) x = x ^ \ शीर्ष M_s x + x ^ \ शीर्ष M_a x = x ^ \ शीर्ष M_s x।$$

हम एक द्विघात कार्य की न्यूनतम तलाश कर रहे हैं

हमें एक आयामी दुनिया में संक्षेप में लौटें; मैं कम से कम फ़ंक्शन खोजना चाहता हूं $$$f (x) = ax ^ 2 - 2bx$ । संख्या $$$एक$ सकारात्मक रूप से, इसलिए न्यूनतम मौजूद है; इसे खोजने के लिए, हम संबंधित व्युत्पन्न को शून्य करने के लिए समान हैं: $$$\ frac {d} {dx} f (x) = 0$ । श्रम के एक आयामी द्विघात कार्य में अंतर नहीं है: $$$\ frac {d} {dx} f (x) = 2ax - 2b = 0$ ; इसलिए हमारी समस्या समीकरण को हल करने के लिए उबालती है $$$कुल्हाड़ी- b = 0$ , जहां, भयानक प्रयासों के माध्यम से, हम एक समाधान प्राप्त करते हैं $$$x ^ * = b / a$ । निम्नलिखित आंकड़ा दो समस्याओं की समानता को दिखाता है: समाधान $$$x ^ *$ समीकरण $$$कुल्हाड़ी- b = 0$ समीकरण के समाधान के साथ मेल खाता है $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ ।



मैं इस तथ्य की ओर जाता हूं कि हमारा वैश्विक लक्ष्य द्विघात कार्यों को कम करना है, लेकिन हम कम से कम वर्गों के बारे में बात कर रहे हैं। लेकिन एक ही समय में, हम वास्तव में क्या जानते हैं कि अच्छा कैसे करना है रैखिक समीकरणों को हल करना है (और रैखिक समीकरणों की प्रणाली)। और यह बहुत अच्छा है कि एक दूसरे के बराबर है!

हमारे लिए एकमात्र चीज यह सुनिश्चित करना है कि एक आयामी दुनिया में यह समानता मामले तक फैली हुई है $$$एन$ चर। इसे सत्यापित करने के लिए, हम पहले तीन प्रमेय सिद्ध करते हैं।

तीन प्रमेय, या मैट्रिक्स अभिव्यक्ति को अलग करते हैं

पहले प्रमेय में कहा गया है कि परिपक्वता $$$1 \ गुना 1$ ट्रांसपोज़ेशन के संबंध में हमलावर:

प्रमेय १

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

प्रमाण इतना जटिल है कि मुझे इसे संक्षिप्तता के लिए छोड़ना होगा, लेकिन इसे स्वयं खोजने का प्रयास करें।

दूसरा प्रमेय हमें रैखिक कार्यों को अलग करने की अनुमति देता है। एक चर के वास्तविक कार्य के मामले में, हम जानते हैं कि $$$\ frac {d} {dx} (bx) = b$ लेकिन एक वास्तविक कार्य के मामले में क्या होता है $$$एन$ चर?

प्रमेय २

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

यही नहीं, आश्चर्य की बात है, एक ही स्कूल परिणाम की एक मैट्रिक्स रिकॉर्डिंग। प्रमाण बेहद सीधा है, बस ढाल की परिभाषा लिखें:

$$

$$\ nlala (b ^ \ top x) = \ start {bmatrix} \ frac {\ आंशिक (b ^ \ शीर्ष x)} {\ आंशिक x_1} \\ \ vdots \\ \ frac {\ आंशिक (b) शीर्ष x)} {\ आंशिक x_n} \ end {bmatrix} = \ start {bmatrix} \ frac {\ आंशिक (b_1 x_1 + \ dots + b_n x_n)} {\ आंशिक x_1} \\ \ vdots \\ \ frac {\ _ आंशिक (b_1 x_1 + \ dots + b_n x_n)} {\ आंशिक x_n} \ end {bmatrix} = \ start {bmatrix} b_1 \\ \ vdots \\ b_n \ end (bmatrix) = b$$

पहले प्रमेय को लागू करना $$$b ^ \ शीर्ष x = x ^ \ शीर्ष b$ , हम सबूत पूरा करते हैं।

अब हम द्विघात रूपों से गुजरते हैं। हम जानते हैं कि एक चर के वास्तविक कार्य के मामले में $$$\ frac {d} {dx} (ax ^ 2) = 2ax$ , और द्विघात रूप के मामले में क्या होगा?

प्रमेय ३

$$$\ nabla (x ^ \ top A x) = (A + A ^ \ top) x$

वैसे, ध्यान दें कि यदि मैट्रिक्स $$$ए$ सममित, फिर प्रमेय कहता है कि $$$\ n नबला (x ^ \ top A x) = 2Ax$ ।

यह प्रमाण भी सीधा है, बस द्विघात के रूप में द्विघात रूप लिखें:

$$

$$x ^ \ शीर्ष A x = \ sum \ limit_i \ sum \ limit_j a_ {ij} x_i 0__$$

और फिर देखते हैं कि चर के संबंध में इस दोहरे योग का आंशिक व्युत्पन्न क्या है $$$x_i$ :
\ start {align *}
\ frac {\ आंशिक (x ^ \ शीर्ष A x)} {\ आंशिक x_i}
& = \ frac {\ आंशिक} {\ आंशिक x_i} \ बाईं (\ योग \ सीमाएं {{k_1} \ _ \ _ सीमाएं} {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} सही) = \\
& = \ frac {\ आंशिक} {\ आंशिक x_i} \ left (
\ underbrace {\ sum \ limit_ {k_1 \ neq i} \ sum \ limit_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ {k_1 \ neq i, k_2 \ neq i} + \ _ अंडरब्रेस {\ _ \ _ लिमिट्स {{k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i, k_2 \ neq i} +
\ underbrace {\ _ \ _ limit_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i, k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i, k_2 = i} \ right) = \\
& = \ _ \ _ सीमाएं {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ _ योग सीमाएं {{k_1 \ neq i} a_ {k_1 i} x_ {k_1} 2 2__ {ii} x_i = \\
& = \ _ \ _ सीमाएं {{k_2} a_ {ik_2} x_ {k_2} + \ sum \ limit_ {k_1} a_ {k_1 i} x_ {k_1} = \\
& = \ _ \ _ limit_ {j} (a_ {ij} + a_ {ji}) x_j_\
\ अंत {संरेखित *}
मैंने दोहरे मामलों को चार मामलों में तोड़ दिया, जिन्हें ब्रेसिज़ द्वारा हाइलाइट किया गया है। इन चार मामलों में से प्रत्येक तुच्छ रूप से भिन्न होता है। यह अंतिम क्रिया करने के लिए बनी हुई है, ग्रेडिएंट वेक्टर में आंशिक व्युत्पत्ति एकत्र करें:

$$

$$\ nlala (x ^ \ top A x) = \ start {bmatrix} \ frac {\ आंशिक (x ^ \ top Ax)} {\ आंशिक x_1} \\ \ vdots \\ \ frac {\ आंशिक = x ^ \ शीर्ष A x)} {\ आंशिक x_n} \ end {bmatrix} = \ start {bmatrix} \ sum \ limit_ {j} (a_ {1j} + a_ {j1}) x_j \\ के \ n \ n \ _ \ _ \ _ \ sum \ limit_ {j} (a_ {nj} + a_ {jn}) x_j \ end {bmatrix} = (A + A ^ \ top) x$$

द्विघात फ़ंक्शन का न्यूनतम और रैखिक प्रणाली का समाधान

यात्रा की दिशा को नहीं भूलना चाहिए। हमने देखा कि सकारात्मक संख्या के साथ $$$एक$ एक चर के वास्तविक कार्यों के मामले में, समीकरण को हल करें $$$कुल्हाड़ी = बी$ या द्विघात फ़ंक्शन को कम से कम करें $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ एक हैं और एक ही चीज हैं।

हम एक सममित सकारात्मक निश्चित मैट्रिक्स के मामले में संबंधित कनेक्शन दिखाना चाहते हैं $$$ए$ ।
इसलिए हम द्विघात कार्य का न्यूनतम पता लगाना चाहते हैं

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n} (x ^ \ top A x - 2b ^ \ top x)। $$$

बिल्कुल स्कूल में, हम व्युत्पन्न को शून्य के बराबर करते हैं:

$$

$$\ nabla (x ^ \ top A x - 2b ^ \ top x) = \ start {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}। $$$

हैमिल्टन ऑपरेटर रैखिक है, इसलिए हम निम्नलिखित रूप में अपने समीकरण को फिर से लिख सकते हैं:

$$

$$\ nabla (x ^ \ top A x) - 2 \ nabla (b ^ \ top x) = \ start {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

अब हम दूसरा और तीसरा भेदभाव सिद्धांत लागू करते हैं:

$$

$$(A + A ^ \ top) x - 2b = \ start {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

उसको याद करो $$$ए$ सममित, और समीकरण को दो में विभाजित करते हैं, हमें उन रैखिक समीकरणों की प्रणाली मिलती है जिनकी हमें आवश्यकता होती है:

$$

$$अक्ष = बी$$

हुर्रे, एक चर से कई तक जा रहे हैं, हमने कुछ भी नहीं खोया है, और हम प्रभावी रूप से द्विघात कार्यों को कम कर सकते हैं!

हम कम से कम वर्गों को पास करते हैं

अंत में, हम इस व्याख्यान की मुख्य सामग्री पर आगे बढ़ सकते हैं। कल्पना कीजिए कि हमारे पास एक विमान पर दो बिंदु हैं $$$(x_1, y_1)$ और $$$(x_2, y_2)$ , और हम इन दो बिंदुओं से गुजरने वाली रेखा के समीकरण को खोजना चाहते हैं। रेखा के समीकरण के रूप में लिखा जा सकता है $$$y = \ अल्फा एक्स + \ बीटा$ , अर्थात्, हमारा कार्य गुणांक ढूंढना है $$$\ अल्फा$ और $$$\ बीटा$ । यह अभ्यास स्कूल की सातवीं-आठवीं कक्षा के लिए है, हम समीकरणों की प्रणाली लिखते हैं:

$$

$$\ बाईं \ {\ _ शुरू {विभाजित} \ अल्फा x_1 + \ बीटा & = y_1 \\ \ अल्फा x_2 + \ beta & = y_2 \\ \ end {विभाजन} \ सही।$$

हमारे पास दो अज्ञात के साथ दो समीकरण हैं ( $$$\ अल्फा$ और $$$\ बीटा$ ), शेष ज्ञात है।

सामान्य मामले में, एक समाधान मौजूद है और अद्वितीय है। सुविधा के लिए, हम मैट्रिक्स रूप में उसी प्रणाली को फिर से लिखते हैं:

$$

$$\ underbrace {\ start {bmatrix} x_1 & 1 \\ x_2 & 1 \ end {bmatrix}} _ _: = A} \ अंडरब्रेस {\ start {bmatrix} \ अल्फा \\ \ बीटा अंत {bmatrix}} _ {: = x} = \ underbrace {\ start {bmatrix} y_1 \\ y_2 \ end {bmatrix}} _ {: = b}$$

हम प्रकार का एक समीकरण प्राप्त करते हैं $$$अक्ष = बी$ जो तुच्छ रूप से हल किया गया है $$$x ^ * = A ^ {- 1} b$ ।

अब कल्पना करें कि हमारे तीन बिंदु हैं जिनके माध्यम से हमें एक सीधी रेखा खींचनी है:

$$

$$\ बाईं \ _ \ _ शुरू {विभाजित} \ अल्फा x_1 + \ बीटा & = y_1 \\ \ अल्फा x_2 + \ बीटा & = y_2 \\ \ अल्फा x_3 + \ बीटा और = y_3 \\ \ अंत {विभाजन} सही ।$$

मैट्रिक्स के रूप में, यह प्रणाली निम्नानुसार लिखी जाती है:

$$

$$\ underbrace {\ start {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}} _ {: = A \ _, (3 \ टाइम्स 2)} \ underbrace (\ start {bmatrix)} \ अल्फा \\ \ बीटा \ अंत {bmatrix}} _ {: = x \; (2 \ बार 1)} = \ underbrace {\ start {bmatrix} y_1 \\ y_2 \\ y_3 \ अंत {brixrix}} _ { : = b \ _, (3 \ _ 1)}$$

अब हमारे पास एक मैट्रिक्स है $$$ए$ आयताकार, और यह बस रिवर्स मौजूद नहीं है! यह पूरी तरह से सामान्य है, क्योंकि हमारे पास केवल दो चर और तीन समीकरण हैं, और सामान्य स्थिति में इस प्रणाली का कोई हल नहीं है। यह वास्तविक दुनिया में एक पूरी तरह से सामान्य स्थिति है, जब अंक शोर माप से डेटा होते हैं, और हमें मापदंडों को खोजने की आवश्यकता होती है $$$\ अल्फा$ और $$$\ बीटा$ सबसे अच्छा अनुमानित माप डेटा। हमने पहले व्याख्यान में इस उदाहरण पर विचार किया था, जब फौलादी अंशांकन किया गया था। लेकिन तब हमारा समाधान शुद्ध रूप से बीजगणित और बहुत बोझिल था। आइए अधिक सहज तरीके से प्रयास करें।

हमारे सिस्टम को इस प्रकार लिखा जा सकता है:

$$

$$\ Alpha \ underbrace {\ start {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ _: = \ vec {i}} + \ beta \ underbrace {\ start \ _ bmatrix} 1 \\ 1 \ _ \ 1 \ end {bmatrix}} _ {: = \ vec {j}} = \ start {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}$$

या, अधिक संक्षेप में,

$$

$$\ Alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}।$$

वैक्टर $$$\ vec मैं$ । $$$\ vec j$ और $$$\ vec b$ ज्ञात है, स्केलर खोजने की जरूरत है $$$\ अल्फा$ और $$$\ बीटा$ ।
जाहिर है रैखिक संयोजन $$$\ Alpha \ vec {i} + \ Beta \ vec {j}$ एक विमान को जन्म देता है, और यदि वेक्टर $$$\ vec b$ इस विमान में झूठ नहीं है, तो कोई सटीक समाधान नहीं है; हालाँकि, हम एक अनुमानित समाधान की तलाश कर रहे हैं।

के रूप में निर्णय त्रुटि को परिभाषित करते हैं $$$\ vec {e} (\ Alpha, \ Beta): = \ Alpha \ vec {i} + \ beta \ vec {j} - \ vec b$ । हमारा लक्ष्य ऐसे पैरामीटर मानों को खोजना है $$$\ अल्फा$ और $$$\ बीटा$ यह वेक्टर की लंबाई को कम करता है $$$\ vec {e} (\ अल्फा, \ बीटा)$ । दूसरे शब्दों में, समस्या के रूप में लिखा है $$$\ mathrm {argmin} _ {\ Alpha, \ beta} \ | \ vec {e} (\ Alpha, \ beta) \ |$ ।
यहाँ एक चित्रण है:



वैक्टर देने के बाद $$$\ vec मैं$ । $$$\ vec j$ और $$$\ vec b$ , हम त्रुटि वेक्टर की लंबाई को कम करने की कोशिश करते हैं $$$\ vec ई$ । जाहिर है, इसकी लंबाई कम से कम है यदि यह वैक्टर पर फैला हुआ विमान के लंबवत है $$$\ vec मैं$ और $$$\ vec j$ ।

लेकिन रुकिए, सबसे कम वर्ग कहां हैं? अब वे होंगे। रूट निष्कर्षण समारोह $$$\ sqrt {\ cdot}$ नीरस इसलिए $$$\ mathrm {argmin} _ {\ Alpha, \ beta} \ | \ vec {e} (\ Alpha, \ beta) \ |$ = $$$\ mathrm {argmin} _ {\ Alpha, \ beta} \ | \ vec {e} (\ Alpha, \ beta) \ | ^ 2$ !

यह काफी स्पष्ट है कि त्रुटि वेक्टर की लंबाई कम हो जाती है अगर यह वैक्टर पर फैला हुआ विमान के लंबवत है $$$\ vec मैं$ और $$$\ vec j$ , जो इसी स्केलर उत्पादों को शून्य करने के लिए लिखा जा सकता है:

$$

$$\ बाएँ \ {\ शुरू {विभाजित} \ vec {i} ^ \ शीर्ष \ vec {e} (\ अल्फा, \ बीटा) & = 0 \\ \ vec {j} ^ \ top \ vec {e} (\ अल्फा, \ बीटा) & = 0 \ end {विभाजन} \ सही।$$

मैट्रिक्स रूप में, यह उसी प्रणाली के रूप में लिखा जा सकता है

$$

$$\ start {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ अंत {bmatrix} \ बाएँ (\ Alpha \ start {bmatrix} x_1 \\ x_2 \\ x_3 \ अंत \ bmatrix} + \ Beta \ start {bmatrix} 1 \\ 1 \\ 1 \\ 1 \ end {bmatrix} - \ start {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ start {bmatrix} \\ 0 \ end {bmatrix }$$

या और

$$

$$\ start {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ अंत {bmatrix} \ बाएँ (\ start {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}) शुरू {bmatrix} \ अल्फा \\ \ बीटा \ अंत {bmatrix} - \ start {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ start {bmatrix} \\ 0 \ end {bmatrix }$$

लेकिन हम वहाँ नहीं रुकेंगे, क्योंकि रिकॉर्ड को और कम किया जा सकता है:

$$

$$A ^ \ top (Ax - b) = \ start {bmatrix} 0 \\ 0 \ end {bmatrix}$$

और सबसे हाल का परिवर्तन:

$$

$$A ^ \ शीर्ष Ax = A ^ \ शीर्ष b।$$

आइए आयामों की गणना करें। मैट्रिक्स $$$ए$ का आकार है $$$3 \ _ 2$ इसलिये $$$ए ^ \ _ टॉप$ का आकार है $$$2 बार 2$ । मैट्रिक्स $$$ब$ का आकार है $$$3 \ गुना 1$ लेकिन वेक्टर $$$ए ^ \ _ टॉप बी$ का आकार है $$$2 बार 1$ । यही है, सामान्य मामले में, मैट्रिक्स $$$ए ^ \ _ टॉप$ प्रतिवर्ती! इसके अलावा, $$$ए ^ \ _ टॉप$ इसमें कुछ अच्छे गुण होते हैं।

प्रमेय ४

$$$ए ^ \ _ टॉप$ सममित।

यह दिखाना मुश्किल नहीं है:

$$

$$(ए ^ \ _ टॉप ए) ^ \ टॉप = ए ^ \ टॉप (ए ^ \ टॉप) ^ \ टॉप = ए ^ टॉप टॉप ए $$$

प्रमेय ५

$$$ए ^ \ _ टॉप$ सकारात्मक रूप से अर्ध-निश्चित: $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geed 0.$

यह इस तथ्य से है कि $$$x ^ \ शीर्ष A ^ \ top A x = (x) ^ \ शीर्ष A x> 0$ ।

इसके अलावा, $$$ए ^ \ _ टॉप$ सकारात्मक निश्चित यदि $$$ए$ रैखिक रूप से स्वतंत्र कॉलम (रैंक) है $$$ए$ प्रणाली में चर की संख्या के बराबर)।

कुल मिलाकर, दो अज्ञात के साथ एक प्रणाली के लिए, हमने साबित किया कि एक द्विघात फ़ंक्शन का न्यूनतमकरण $$$\ mathrm {argmin} _ {\ Alpha, \ beta} \ | \ vec {e} (\ Alpha, \ beta) \ | ^ 2$ रैखिक समीकरणों की एक प्रणाली को हल करने के बराबर $$$A ^ \ top A x = A ^ \ b b$ । बेशक, यह सब तर्क किसी अन्य संख्या में चर पर लागू होता है, लेकिन आइए एक साधारण बीजगणितीय गणना के साथ फिर से सब कुछ एक साथ लिखें। हम कम से कम वर्गों की समस्या से शुरू करते हैं, परिचित रूप के द्विघात फ़ंक्शन के न्यूनतम पर आते हैं, और इससे हम निष्कर्ष निकालते हैं कि यह रैखिक समीकरणों की एक प्रणाली को हल करने के बराबर है। तो, चलिए चलते हैं:

$$

$$\ start {विभाजित} \ mathrm {argmin} \ | Ax - b \ _ ^ 2 & = \ mathrm {argmin} (Ax-b) ^ \ top (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ टॉप - b \ _) शीर्ष) (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - b ^ \ top Ax - x ^ \ top A ^ \ top b + \ underbrace {b ^ \ Top b} _ {\ rm const}) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - 2b ^ \ top Ax) = \\ & = \ mathrm {armmin} ( x ^ \ टॉप \ अंडरब्रेस {(ए ^ \ टॉप ए)} _ {: = ए '} एक्स - 2 \ अंडरब्रेस {(ए ^ \ टॉप बी)} _ {: = b'} \ प्रेत {} ^ टॉप x) \ end {विभाजित}$$

तो कम से कम वर्गों की समस्या $$$\ mathrm {argmin} \ | कुल्हाड़ी - b \ _ ^ 2$ एक द्विघात समारोह को कम करने के बराबर $$$\ mathrm {argmin} (x ^ \ top A 'x - 2b' ^ \ top x)$ (सामान्य मामले में) एक सममित सकारात्मक निश्चित मैट्रिक्स $$$ए ’$ , जो बदले में, रैखिक समीकरणों की एक प्रणाली को हल करने के बराबर है $$$A'x = b '$ । वाह। सिद्धांत खत्म हो गया है।

अभ्यास के लिए आगे बढ़ते हैं

उदाहरण वन, वन-डायमेंशनल

आइए पिछले लेख के एक उदाहरण को याद करते हैं:

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

हमारे पास 32 तत्वों की एक नियमित एक्स सरणी है, जो इस प्रकार है:



और फिर हम निम्नलिखित प्रक्रिया को एक हजार बार करेंगे: प्रत्येक सेल x [i] के लिए हम इसमें पड़ोसी कोशिकाओं का औसत मान लिखते हैं: x [i] = (x [i-1] + x [i + 1]) / 2। एकमात्र अपवाद: हम संख्या 0, 18 और 31 के साथ सरणी के तत्वों को फिर से नहीं लिखेंगे। इस प्रकार सरणी का विकास पहले सौ और पचास पुनरावृत्तियों में दिखता है:



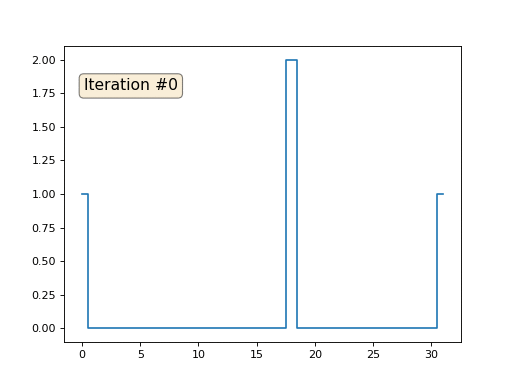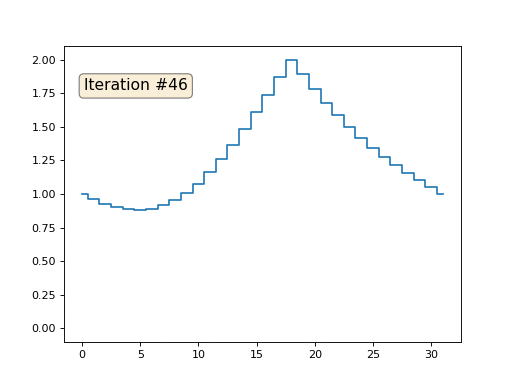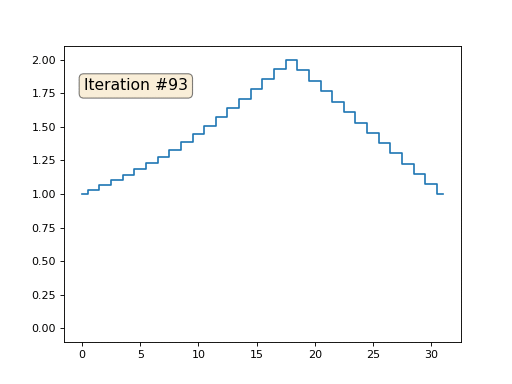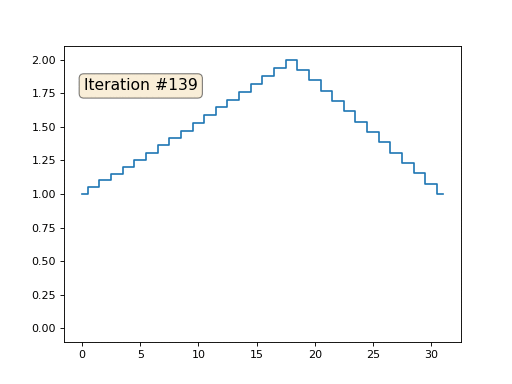
जैसा कि हमने पिछले लेख में पाया था, यह पता चला है कि हमारे चार-लाइन पायथन कोड मेगाकॉड, गॉस-सीडेल विधि द्वारा रैखिक समीकरणों की निम्न प्रणाली को हल करते हैं:



उन्हें पता चला, लेकिन यह व्यवस्था कहां से आई? कैसा जादू? आइए एक दूसरे के लिए खुदाई करें, और थोड़ा अलग सिस्टम को हल करने का प्रयास करें। मेरे पास अभी भी 32 चर हैं, लेकिन अब मैं चाहता हूं कि वे सभी एक-दूसरे के बराबर हों। यह लिखना मुश्किल नहीं है, यह समीकरणों की एक प्रणाली को लिखने के लिए पर्याप्त है जो बताता है कि सभी पड़ोसी तत्व जोड़े में समान हैं:



उपरोक्त पायथन कोड, सिद्धांत रूप में, तीन चर के मूल्यों को नहीं छूता है: x0, x18, x31, इसलिए आइए उन्हें समीकरणों की प्रणाली के दाईं ओर स्थानांतरित करें, अर्थात, अज्ञात के सेट से बाहर करें



मैं प्रारंभिक मान x0 = 1 को ठीक करता हूं, पहला समीकरण X1 = x0 = 1 कहता है, दूसरा समीकरण कहता है x2 = X1 = x0 = 1 और इसी तरह, जब तक हम समीकरण 1 = x0 = x17 = x18 = 2 नहीं प्राप्त करते हैं । ओह। लेकिन इस प्रणाली का कोई हल नहीं है: (

और परवाह नहीं है, हम प्रोग्रामर हैं! चलो मदद के लिए कम से कम वर्गों को बुलाओ! हमारी असाध्य प्रणाली को मैट्रिक्स के रूप में लिखा जा सकता है $$$अक्ष = बी$ ; हमारी प्रणाली को हल करने के लिए, यह प्रणाली को हल करने के लिए पर्याप्त है $$$A^\top Ax=A^\top b$ ।और फिर यह पता चला कि यह पिछले लेख से समीकरणों की एक-में-एक प्रणाली है!

सहज रूप से, एक सिस्टम की एक मैट्रिक्स बनाने की प्रक्रिया की कल्पना इस प्रकार कर सकता है: हम उन मूल्यों को स्प्रिंग्स द्वारा जोड़ते हैं जिनकी समानता हम प्राप्त करना चाहते हैं। उदाहरण के लिए, हमारे मामले में, हम चाहते हैं$$x i बराबर था$x_i$$$x i + 1 है , इसलिए हम समीकरण जोड़ते हैं$x_{i+1}$$$x i - x i + 1 = 0 , इन मूल्यों के बीच एक वसंत है जो उन्हें एक साथ खींच देगा। लेकिन चूंकि x0, x18, और x31 के मूल्य दृढ़ता से तय किए गए हैं, मुफ्त मूल्यों के लिए स्प्रिंग्स को समान रूप से खींचने के लिए कुछ भी नहीं बचा है, उत्पादन (इस मामले में) एक टुकड़ा-रेखीय समाधान। आइए एक कार्यक्रम लिखें जो समीकरणों की इस प्रणाली को हल करता है। पिछले लेख में, हमने देखा कि गॉस-सीडेल विधि प्रोग्रामिंग में बहुत सरल है, लेकिन बहुत धीमी गति से अभिसरण है, इसलिए रैखिक समीकरणों के सिस्टम के वास्तविक सॉल्वर का उपयोग करना बेहतर होगा। सबसे सरल मामले में, हमारे एक-आयामी उदाहरण के लिए, कोड कुछ इस तरह दिख सकता है:$x_i - x_{i+1}=0$

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

यह कोड 32 तत्वों की एक सूची x उत्पन्न करता है जिसमें समाधान संग्रहीत किया जाता है। हम एक मैट्रिक्स का निर्माण कर रहे हैं$$ए , एक वेक्टर का निर्माण$ए$$$बी , हम एक सॉल्यूशन के साथ एक वेक्टर प्राप्त करते हैं$ब$$$एक्स = ( एक ⊤ एक ) - 1 एक ⊤ ख , और इस वेक्टर में तो डाला हमारे निश्चित मान x0 = 1, x18 = x31 = 2 और 1। यह कोड आवश्यक कार्य करता है, लेकिन निश्चित चर के मूल्यों को दाईं ओर स्थानांतरित करना अप्रिय है। क्या धोखा देना संभव है? आप कर सकते हैं! आइए निम्नलिखित कोड देखें:$x = (A^\top A)^{-1}A^\top b$

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

एक प्रोग्रामर के दृष्टिकोण से, यह बहुत अच्छा है, वेक्टर x आवश्यक आयाम के तुरंत प्राप्त किया जाता है, और मैट्रिक्स ए और बी बहुत आसान में भरे जाते हैं। लेकिन चाल क्या है? आइए हम जो समीकरणों को हल करते हैं, उन्हें लिखें:



पिछले तीन समीकरणों को ध्यान से देखें:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1

क्या उन्हें इस प्रकार लिखना आसान हो सकता है?
x0 = 1
x18 = 2
x31 = 1

नहीं, आसान नहीं है। जैसा कि मैंने पहले ही कहा, प्रत्येक समीकरण स्प्रिंग्स लटकाता है, इस मामले में, x0 और मान 1 के बीच वसंत, x18 और मान 2 के बीच वसंत, और अंत में, चर x31 भी एकता के लिए आकर्षित होगा।

लेकिन 100 का गुणांक एक कारण से है। हमें याद है कि इस प्रणाली को सिर्फ हल नहीं किया जा सकता है, हम इसे कम से कम वर्गों के अर्थ में हल करते हैं, जो संबंधित द्विघात फ़ंक्शन को न्यूनतम करता है। पिछले तीन समीकरणों के 100 गुणांक में से प्रत्येक को गुणा करते हुए, हम वांछित मानों से x0, x18 और x32 के विचलन के लिए एक दंड पेश करते हैं, दस हजार गुना (100 ^ 2) समानता से भटकने के लिए दंड को पार करते हैं।$$$x_i = x_{i+1}$ ।मोटे तौर पर, पिछले तीन समीकरणों पर स्प्रिंग्स अन्य सभी की तुलना में दस हजार गुना कठिन है। यह द्विघात दंड विधि प्रतिबंधों को लागू करने के लिए एक बहुत ही सुविधाजनक उपकरण है, यह चर का एक सेट कम करने की तुलना में बहुत सरल (हालांकि कमियां के बिना नहीं) है।

उदाहरण दो, तीन आयामी

चलो एक आयामी सरणी के तत्वों को चौरसाई करने की तुलना में अधिक दिलचस्प कुछ पर चलते हैं! के साथ शुरू करने के लिए, हम बिल्कुल वैसा ही करेंगे, लेकिन अधिक दिलचस्प डेटा और वास्तविक उपकरणों के साथ। मैं एक त्रि-आयामी सतह लेना चाहता हूं, इसकी सीमा तय करता हूं, और बाकी सतह को जितना संभव हो उतना चिकना कर सकता हूं :



कोड यहां उपलब्ध है , लेकिन सिर्फ मामले में मैं मुख्य फाइल की पूरी सूची दूंगा:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

मैंने वेवफ्रंट .obj फ़ाइलों का सबसे सरल पार्सर लिखा है, इसलिए मॉडल एक पंक्ति में लोड किया गया है। एक सॉल्वर के रूप में, मैं ओपनएनएल का उपयोग करूंगा, यह विरल मैट्रेस के साथ कम से कम वर्गों की समस्याओं के लिए एक बहुत शक्तिशाली सॉल्वर है। कृपया ध्यान दें कि मैट्रिक्स के आयाम विशाल हो सकते हैं: उदाहरण के लिए, यदि हम 1000 x 1000 पिक्सल के आकार के साथ एक काले और सफेद चित्र प्राप्त करना चाहते हैं, तो मैट्रिक्स$$A per A हमारे पास प्रति मिलियन लाख का आकार होगा! हालांकि, व्यवहार में, इस मैट्रिक्स के अधिकांश तत्व अक्सर शून्य होते हैं, इसलिए सब कुछ इतना डरावना नहीं है, लेकिन आपको अभी भी विशेष सॉल्वर का उपयोग करने की आवश्यकता है। तो आइए कोड को देखें। शुरू करने के लिए, मैं सॉल्वर की घोषणा करता हूं कि मैं क्या करना चाहता हूं:$A^\top A$

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

मुझे एक मैट्रिक्स चाहिए $$एक ⊤ एक आकार (Colville कोने) x (Colville कोने)। ध्यान दें, हम सॉल्वर को एक मैट्रिक्स देते हैं$A^\top A$$$ए , और$ए$$$A very A वह इसका निर्माण स्वयं करेगा, जो बहुत सुविधाजनक है! इसके अलावा, इस तथ्य पर ध्यान दें कि मैं समीकरणों की एक प्रणाली को हल नहीं करता हूं, लेकिन एक्स, वाई और जेड के लिए श्रृंखला में तीन (मैंने झूठ बोला था कि समस्या तीन आयामी है, यह अभी भी एक आयामी है!)और फिर मैं हमारे मैट्रिक्स की पंक्ति द्वारा पंक्ति घोषित करता हूं। शुरू करने के लिए, मैं सतह के किनारे पर खड़े कोने को ठीक करता हूं:$A^\top A$

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

आप देख सकते हैं कि मैं किनारे के कोने को ठीक करने के लिए 100 ^ 2 के वर्ग दंड का उपयोग कर रहा हूं।

खैर, फिर आसन्न कोने की प्रत्येक जोड़ी के लिए मैं उनके बीच कठोरता 1 का एक वसंत लटकाता हूं:

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

हम कोड को निष्पादित करते हैं और देखते हैं कि घुमावदार तार पर साबुन फिल्म की सतह में चेहरा कैसे चिकना हुआ है। हमने न्यूनतम क्षेत्र की सतह प्राप्त करते हुए, डिरिक्लेट समस्या को हल कर दिया है।

हम विशेषताओं को बढ़ाते हैं

आइए हमारे चेहरे को एक गॉकेटेक मास्क में बदल दें:



पिछले लेख में मैंने पहले ही दिखाया था कि घुटने पर यह कैसे करना है, यहां मैं एक वास्तविक कोड देता हूं जो कम से कम चौकों का उपयोग करता है:

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

पूर्ण कोड यहाँ उपलब्ध है । वह कैसे काम करता है? पिछले उदाहरण के रूप में, मैं किनारे के कोने को ठीक करके शुरू करता हूं। फिर प्रत्येक किनारे के लिए मैं (चुपचाप, 0.2 के गुणांक के साथ) कहता हूं कि यह अच्छा होगा यदि इसका मूल सतह के समान आकार हो:

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

यदि आप कुछ और नहीं करते हैं और समस्या को वैसे ही हल करते हैं, तो हमें आउटपुट में आउटपुट पर ठीक वैसा ही मिलना चाहिए: आउटपुट बॉर्डर इनपुट बॉर्डर के बराबर होता है, साथ ही आउटपुट में अंतर इनपुट के अंतर के बराबर होता है।

लेकिन हम वहाँ नहीं रुकेंगे!

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

मैं हमारे सिस्टम में अधिक समीकरण जोड़ता हूं। प्रत्येक शीर्ष के लिए, मैं इनपुट सतह में इसके चारों ओर की सतह की वक्रता की गणना करता हूं, और इसे ढाई से गुणा करता हूं, अर्थात आउटपुट सतह में हर जगह एक बड़ी वक्रता होनी चाहिए।

फिर हम अपने सॉल्वर को बुलाते हैं और एक अच्छा कैरिकेचर प्राप्त करते हैं।

आज के लिए अंतिम उदाहरण

इस क्षण तक, हमने एक भी नया उदाहरण नहीं देखा है, सब कुछ पहले से ही पिछले लेख में दिखाया गया था। आइए सबसे सरल चौरसाई की तुलना में कुछ कम तुच्छ काम करने की कोशिश करें, जो किसी भी सॉल्वर का उपयोग किए बिना आसानी से प्राप्त किया जा सकता है। यहाँ कोड उपलब्ध है , लेकिन मैं आपको एक सूची दूंगा:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

हम अभी भी पहले की तरह ही सतह पर काम कर रहे हैं; हम प्रत्येक त्रिकोण के लिए स्नैप () फ़ंक्शन कहते हैं। यह फ़ंक्शन कहता है कि समन्वय प्रणाली का कौन सा अक्ष इस त्रिकोण के सामान्य के सबसे करीब है। यही है, हम जानना चाहते हैं कि यह त्रिभुज अधिक लंबवत या क्षैतिज है। ठीक है, तो हम अपनी सतह की ज्यामिति को बदलना चाहते हैं ताकि क्षैतिज के करीब जो हो वह और भी करीब हो जाए! इस तस्वीर का बायां हिस्सा स्नैप () फ़ंक्शन का परिणाम दिखाता है:



इसलिए, हमने समन्वय प्रणाली के तीन अक्षों के अनुरूप, हमारी सतह को तीन रंगों में चित्रित किया है। फिर, हमारे सिस्टम के प्रत्येक किनारे के लिए हम निम्नलिखित समीकरण जोड़ते हैं:

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

यही है, हम आउटपुट सतह के प्रत्येक किनारे को इनपुट सतह के संबंधित किनारे से मिलते जुलते बनाने का निर्देश देते हैं। वसंत की कठोरता 1. और फिर, यदि हम अनुमति देते हैं, उदाहरण के लिए, आयाम x, और किनारे को लंबवत होना चाहिए, तो हम बस यह कहते हैं कि वसंत की कठोरता के साथ एक शीर्ष दूसरे के बराबर है। 2:

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

खैर, यहां हमारे कार्यक्रम का परिणाम है: एक



पूरी तरह से उचित प्रश्न: ईस्टर द्वीप से मूर्तियों, यह, ज़ाहिर है, शांत है, लेकिन भूविज्ञान का इससे क्या लेना-देना है? क्या वास्तविक समस्याओं के कोई उदाहरण हैं?

हां बिल्कुल।चलो पृथ्वी की पपड़ी का एक खंड लेते हैं:



भूवैज्ञानिकों के लिए, विभिन्न चट्टानों की परतें बहुत महत्वपूर्ण हैं, सीमाएं (क्षितिज) जिनके बीच हरे रंग में दिखाई जाती हैं, और भूवैज्ञानिक दोष जो लाल रंग में दिखाए जाते हैं। हमारे पास उस क्षेत्र के त्रिभुजों (3 डी में टेट्राहेड्रोन) का एक ग्रिड है, जो हमें रुचता है, लेकिन कुछ प्रक्रियाओं को मॉडल करने के लिए क्वाड्स (3 डी में हेक्साहेड्रोन) की आवश्यकता होती है। हम अपने मॉडल को विकृत करते हैं ताकि दोष ऊर्ध्वाधर हो जाएं और क्षितिज (आश्चर्य) क्षैतिज:



फिर हम बस वर्गों का एक नियमित ग्रिड लेते हैं, हमारे डोमेन को एकसमान वर्गों में काटते हैं, और उन्हें विपरीत परिवर्तन लागू करते हैं, जिससे क्वैड्स की आवश्यक ग्रिड प्राप्त होती है।

निष्कर्ष

कम से कम चौकोर तरीके एक शक्तिशाली डेटा प्रोसेसिंग टूल हैं, और इनका उपयोग एक्सेल कॉलम में आँकड़ों की तुलना में अधिक व्यापक रूप से किया जाता है। इन संभावनाओं को इस तथ्य के कारण खोला जाता है कि एक द्विघात फ़ंक्शन को कम करना और रैखिक समीकरणों की एक प्रणाली को हल करना एक और एक ही है, और हमने (मानवता) रैखिक समीकरणों को हल करने के लिए सीखा है, बहुत अच्छी तरह से, अरबों चर के पूरी तरह से अमानवीय आकार।

हालांकि, ऐसे समय होते हैं जब हमारे पास पर्याप्त रैखिक मॉडल नहीं हो सकते हैं। और यहां, उदाहरण के लिए, तंत्रिका नेटवर्क बचाव में आ सकते हैं। अगले लेख में, मैं यह दिखाने की कोशिश करूंगा कि उत्सर्जन की अस्वीकृति वाला ओएलएस तंत्रिका नेटवर्क के योगों में से एक के बराबर है। लाइन पर रहो!