दूसरी प्रोग्रामिंग चैम्पियनशिप: हम एमएल-ट्रैक के कार्यों का विश्लेषण करते हैं

अक्टूबर में, दूसरी प्रोग्रामिंग चैम्पियनशिप आयोजित की गई थी। हमें 12,500 आवेदन मिले, 6,000 से अधिक लोगों ने प्रतियोगिताओं में अपना हाथ आजमाया। इस बार, प्रतिभागी निम्नलिखित में से किसी एक ट्रैक को चुन सकते हैं: बैकएंड, फ्रंटेंड, मोबाइल डेवलपमेंट और मशीन लर्निंग। प्रत्येक ट्रैक में, योग्यता चरण और अंतिम उत्तीर्ण करना आवश्यक था।

परंपरा से, हम हैबे पर पटरियों का विश्लेषण प्रकाशित करेंगे। आइए मशीन सीखने के योग्यता चरण के कार्यों से शुरू करें। टीम ने पांच ऐसे कार्य तैयार किए, जिनमें से तीन कार्यों के लिए दो विकल्प थे: पहले संस्करण में ए 1, बी 1 और सी थे, दूसरे में - ए 2, बी 2 और सी। प्रतिभागियों के बीच विकल्पों को यादृच्छिक रूप से वितरित किया गया था। टास्क सी के लेखक हमारे डेवलपर पावेल पार्कहोमेंको हैं, बाकी कार्य उनके सहयोगी निकिता सेंडरोविच द्वारा किए गए थे।

पहले सरल एल्गोरिथमिक कार्य (A1 / A2) के लिए, प्रतिभागी उत्तर की सही गणना करके 50 अंक प्राप्त कर सकते हैं। दूसरे कार्य (बी 1 / बी 2) के लिए हमने 10 से 100 अंक दिए - समाधान की प्रभावशीलता पर निर्भर करता है। 100 अंक प्राप्त करने के लिए, गतिशील प्रोग्रामिंग विधि को लागू करना आवश्यक था। तीसरा कार्य प्रदान किए गए प्रशिक्षण डेटा के आधार पर एक क्लिक मॉडल के निर्माण के लिए समर्पित था। यह श्रेणीबद्ध विशेषताओं के साथ काम करने के तरीकों को लागू करने और प्रशिक्षण के गैर-रैखिक मॉडल का उपयोग करने के लिए आवश्यक है (उदाहरण के लिए, ग्रेडिएंट बूस्टिंग)। कार्य के लिए 150 अंक तक प्राप्त करना संभव था - परीक्षण नमूने पर नुकसान फ़ंक्शन के मूल्य पर निर्भर करता है।

A1। हिंडोला की लंबाई को पुनर्स्थापित करें

शर्त

सिफारिश प्रणाली को प्रभावी ढंग से लोगों के हितों का निर्धारण करना चाहिए। और मशीन सीखने के तरीकों के अलावा, इस कार्य को करने के लिए विशेष इंटरफ़ेस समाधानों का उपयोग किया जाता है, जो उपयोगकर्ता से स्पष्ट रूप से पूछते हैं कि उसके लिए क्या दिलचस्प है। ऐसा ही एक समाधान हिंडोला है।

एक हिंडोला कार्ड का एक क्षैतिज रिबन है, जिनमें से प्रत्येक एक विशिष्ट स्रोत या विषय की सदस्यता के लिए प्रदान करता है। एक ही कार्ड हिंडोला में कई बार पाया जा सकता है। हिंडोला को बाएं से दाएं स्क्रॉल किया जा सकता है, जबकि अंतिम कार्ड के बाद उपयोगकर्ता फिर से पहला देखता है। उपयोगकर्ता के लिए, अंतिम कार्ड से पहली बार संक्रमण अदृश्य है, उसकी दृष्टि से टेप अंतहीन है।

कुछ बिंदु पर, एक जिज्ञासु उपयोगकर्ता वसीली ने देखा कि टेप वास्तव में लूप किया गया था, और हिंडोला की वास्तविक लंबाई का पता लगाने का फैसला किया। ऐसा करने के लिए, उन्होंने टेप के माध्यम से स्क्रॉल करना शुरू किया और क्रमिक रूप से मीटिंग कार्ड्स को सरलता के लिए लिखा, प्रत्येक कार्ड को लोअरकेस लैटिन अक्षर के साथ नामित किया। तो वासिली ने कागज के एक टुकड़े पर पहला एन कार्ड लिखा। यह गारंटी है कि उसने कम से कम एक बार सभी हिंडोला कार्ड को देखा। फिर वसीली बिस्तर पर चला गया, और सुबह उसे पता चला कि किसी ने उसके नोटों पर एक गिलास पानी गिरा दिया था और अब कुछ पत्रों को मान्यता नहीं दी जा सकती थी।

शेष जानकारी के अनुसार, हिंडोला में हिंडोला की सबसे छोटी संभव संख्या निर्धारित करने में मदद करें।

रेटिंग प्रणाली

कार्य के लिए सभी परीक्षण पास करने के बाद ही आप 50 अंक प्राप्त कर सकते हैं।

परीक्षण प्रणाली में, 1-4 परीक्षण हालत से उदाहरण हैं।

निर्णय

यह हिंडोला की संभावित लंबाई को 1 से n तक हल करने के लिए पर्याप्त था और प्रत्येक निश्चित लंबाई की जांच के लिए कि क्या यह ऐसा हो सकता है। यह स्पष्ट है कि उत्तर हमेशा मौजूद होता है, क्योंकि n का मान एक संभावित उत्तर होने की गारंटी है। एक निश्चित हिंडोला लंबाई पी के लिए, यह सत्यापित करने के लिए पर्याप्त है कि सभी पदों i, i + p, i + 2p, आदि पर 0 से लेकर (p - 1) के लिए संचरित स्ट्रिंग में, समान वर्ण या # पाए जाते हैं। यदि कम से कम कुछ के लिए मैं एक z से सीमा तक 2 अलग-अलग वर्ण हैं, तो हिंडोला लंबाई p का नहीं हो सकता है। चूंकि सबसे खराब स्थिति में, प्रत्येक पी के लिए, आपको एक बार स्ट्रिंग के सभी पात्रों के माध्यम से चलाने की आवश्यकता है, इस एल्गोरिथ्म की जटिलता ओ (एन ² ) है।

 def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break 

ए 2। हिंडोला की लंबाई को पुनर्स्थापित करें

शर्त

सिफारिश प्रणाली को प्रभावी ढंग से लोगों के हितों का निर्धारण करना चाहिए। और मशीन सीखने के तरीकों के अलावा, इस कार्य को करने के लिए विशेष इंटरफ़ेस समाधानों का उपयोग किया जाता है, जो उपयोगकर्ता से स्पष्ट रूप से पूछते हैं कि उसके लिए क्या दिलचस्प है। ऐसा ही एक समाधान हिंडोला है।

एक हिंडोला कार्ड का एक क्षैतिज रिबन है, जिनमें से प्रत्येक एक विशिष्ट स्रोत या विषय की सदस्यता के लिए प्रदान करता है। एक ही कार्ड हिंडोला में कई बार पाया जा सकता है। हिंडोला को बाएं से दाएं स्क्रॉल किया जा सकता है, जबकि अंतिम कार्ड के बाद उपयोगकर्ता फिर से पहला देखता है। उपयोगकर्ता के लिए, अंतिम कार्ड से पहली में संक्रमण अदृश्य है, उसकी दृष्टि से टेप अंतहीन है।

कुछ बिंदु पर, एक जिज्ञासु उपयोगकर्ता वसीली ने देखा कि टेप वास्तव में लूप किया गया था, और हिंडोला की वास्तविक लंबाई का पता लगाने का फैसला किया। ऐसा करने के लिए, उसने टेप के माध्यम से स्क्रॉल करना शुरू कर दिया और क्रमिक रूप से मीटिंग कार्ड्स को सरलता के लिए लिखने के लिए, प्रत्येक कार्ड को लोअरकेस लैटिन अक्षर के साथ नामित किया। तो वसीली ने पहले n कार्ड्स लिखे। यह गारंटी है कि उसने कम से कम एक बार सभी हिंडोला कार्ड को देखा। चूंकि वासिली को कार्ड की सामग्री से विचलित किया गया था, जब बाहर लिखते हुए, वह गलती से एक अक्षर को दूसरे के साथ बदल सकता था, लेकिन यह ज्ञात है कि कुल मिलाकर उसने k गलतियों से अधिक नहीं बनाया।

वासिली द्वारा बनाई गई रिकॉर्डिंग आपके हाथों में गिर गई, आप कश्मीर का मूल्य भी जानते हैं। निर्धारित करें कि उसके हिंडोला में कितने कार्ड हो सकते हैं।

रेटिंग प्रणाली

कार्य के लिए सभी परीक्षण पास करने के बाद ही आप 50 अंक प्राप्त कर सकते हैं।

परीक्षण प्रणाली में, 1-4 परीक्षण हालत से उदाहरण हैं।

निर्णय

यह हिंडोला की संभावित लंबाई को 1 से n तक हल करने के लिए पर्याप्त था और प्रत्येक निश्चित लंबाई की जांच के लिए कि क्या यह ऐसा हो सकता है। यह स्पष्ट है कि उत्तर हमेशा मौजूद होता है, क्योंकि n का मान एक संभावित उत्तर होने की गारंटी है, जो भी k का मूल्य है। एक निश्चित हिंडोला लंबाई पी के लिए, यह स्वतंत्र रूप से 0 से लेकर (पी - 1) तक सभी के लिए स्वतंत्र रूप से गणना करने के लिए पर्याप्त है, मैं, i + p, i + 2p इत्यादि पदों पर न्यूनतम त्रुटियों की संख्या क्या है, अगर यह सही है, तो त्रुटियों की संख्या न्यूनतम है। प्रतीक वह है जो इन पदों पर सबसे अधिक बार पाया जाता है। फिर त्रुटियों की संख्या उन पदों की संख्या के बराबर होती है जिन पर एक और पत्र खड़ा होता है। यदि कुछ p के लिए त्रुटियों की कुल संख्या k से अधिक नहीं है, तो मान p एक संभावित उत्तर है। चूंकि प्रत्येक पी के लिए आपको एक बार स्ट्रिंग के सभी पात्रों पर जाने की आवश्यकता होती है, इस एल्गोरिथ्म की जटिलता ओ (एन ² ) है।

 n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break 

बी 1। इष्टतम सिफारिश टेप

शर्त

उपयोगकर्ता के लिए सिफारिशों को जारी करने वाले व्यक्तिगत हिस्से के अगले भाग का गठन एक आसान काम नहीं है। उम्मीदवारों के चयन के आधार पर सिफारिश आधार से चुने गए एन प्रकाशनों पर विचार करें। प्रकाशन संख्या i की प्रासंगिकता स्कोर _i और k बाइनरी विशेषताओं का एक सेट _i1 , _i2 , ..., एक _{ik है} । इन विशेषताओं में से प्रत्येक प्रकाशन की कुछ संपत्ति से मेल खाती है, उदाहरण के लिए, क्या उपयोगकर्ता इस प्रकाशन के स्रोत के लिए सदस्यता लेता है, चाहे प्रकाशन पिछले 24 घंटों में बनाया गया था, आदि। प्रकाशन में इन गुणों में से कई एक साथ हो सकते हैं, जिस स्थिति में संबंधित विशेषताओं का मूल्य होता है। 1, या इसमें से कोई भी नहीं हो सकता है - और फिर इसकी सभी विशेषताएं 0 हैं।

उपयोगकर्ता की फ़ीड विविध होने के लिए, यह आवश्यक है कि मी अभ्यर्थी n प्रकाशनों में से किसी एक को चुनें ताकि उनके बीच कम से कम A ₁ प्रकाशन हो, जिसमें पहली संपत्ति हो, कम से कम A ₂ प्रकाशनों में दूसरी संपत्ति हो, ..., A _k प्रकाशनों की संपत्ति वाले प्रकाशन नंबर के। मी प्रकाशनों के लिए अधिकतम संभव कुल प्रासंगिकता स्कोर प्राप्त करें जो इस आवश्यकता को पूरा करते हैं, या यह निर्धारित करते हैं कि इस तरह का प्रकाशन मौजूद नहीं है।

रेटिंग प्रणाली

इस कार्य के लिए परीक्षण में पाँच समूह शामिल हैं। प्रत्येक समूह के अंक केवल समूह के सभी परीक्षणों और पिछले समूहों के सभी परीक्षणों को पास करते समय दिए जाते हैं। दूसरे से शुरू होने वाले समूहों के लिए अंक प्राप्त करने के लिए शर्तों से परीक्षण पास करना आवश्यक है। कार्य के लिए कुल मिलाकर आप 100 अंक प्राप्त कर सकते हैं।

परीक्षण प्रणाली में, परीक्षण 1-2 स्थिति से उदाहरण हैं।

1. (10 अंक) परीक्षण 3-10: k = 1, m ≤ 3, s _i , 1000, कोई भी परीक्षण शर्त से आवश्यक नहीं हैं
2. (20 अंक) टेस्ट 11–20: k m 2, m tests 3
3. (20 अंक) परीक्षण 21–29: k tests 2
4. (20 अंक) परीक्षण 30-37: k tests 3
5. (30 अंक) परीक्षण 38-47: कोई अतिरिक्त प्रतिबंध नहीं

निर्णय

N प्रकाशन हैं, प्रत्येक में गति और k बूलियन झंडे हैं, मी कार्ड्स का चयन करना आवश्यक है, जैसे कि प्रासंगिकता की राशि अधिकतम है और प्रपत्र की k आवश्यकताएं "चयनित m प्रकाशनों में ≥ ए-आई ध्वज के साथ एक _i कार्ड होना चाहिए" पूरी हो गई हैं, या यह निर्धारित करते हैं कि इस तरह के प्रकाशन का कोई अस्तित्व नहीं है।

निर्णय 10 अंक है : यदि वास्तव में एक ध्वज है, तो इस ध्वज के साथ A ₁ प्रकाशन लेने के लिए पर्याप्त है जो सबसे अधिक प्रासंगिक हैं (यदि A ₁ से कम ऐसे कार्ड हैं, तो वांछित सेट मौजूद नहीं है), और बाकी (m - A ₁ ) को ऊपर ले जाना चाहिए। सबसे अच्छी प्रासंगिकता वाले कार्ड।

समाधान 30 अंक है : यदि मी 3 से अधिक नहीं है, तो आप कार्ड के सभी संभावित ओ (एन ³ ) परीक्षणों की संपूर्ण खोज के द्वारा उत्तर पा सकते हैं, प्रतिबंधों को संतुष्ट करने वाली कुल प्रासंगिकता के संदर्भ में सबसे अच्छा विकल्प चुनें।

निर्णय 70 अंक (50 अंक समान है, केवल लागू करना आसान है): यदि 3 से अधिक झंडे नहीं हैं, तो आप सभी प्रकाशनों को 8 असंतुष्ट समूहों में विभाजित कर सकते हैं, उनके पास मौजूद झंडे के सेट के अनुसार: 000, 001, 010, 011, 100, 101, 110, 111. प्रत्येक समूह में प्रकाशनों को प्रासंगिकता के अवरोही क्रम में क्रमबद्ध किया जाना चाहिए। फिर, O (m ⁴ ) के लिए, हम समूहों को 111, 011, 110 और 101 में से कितने सर्वश्रेष्ठ प्रकाशन निकाल सकते हैं। प्रत्येक से हम 0 से m प्रकाशनों तक ले जाते हैं, कुल मिलाकर मी से अधिक नहीं। उसके बाद, यह स्पष्ट हो जाता है कि आवश्यकताओं को पूरा करने के लिए समूह 100, 010 और 001 से कितने प्रकाशनों की आवश्यकता है। यह सबसे अच्छी प्रासंगिकता के साथ शेष कार्डों के साथ मी पर बना हुआ है।

पूर्ण समाधान : डायनामिक प्रोग्रामिंग फंक्शन dp [i] [a] ... [z] पर विचार करें। यह अधिकतम कुल प्रासंगिकता स्कोर है जिसे वास्तव में i प्रकाशनों का उपयोग करके प्राप्त किया जा सकता है ताकि झंडे A, ..., Z प्रकाशनों के साथ Z के साथ एक प्रकाशन हो। फिर, शुरू में dp [0] [0] ... [0] = 0, और सभी अन्य मापदंडों के लिए हम भविष्य में इस मूल्य को अधिकतम करने के लिए -1 के बराबर मूल्य सेट करते हैं। अगला, हम एक बार में "गेम में प्रवेश करेंगे" कार्ड और प्रत्येक कार्ड का उपयोग इस फ़ंक्शन के मूल्यों में सुधार करने के लिए करेंगे: प्रत्येक राज्य की गतिशीलता के लिए (i, a, b, ..., z) झंडे के साथ j- वें प्रकाशन का उपयोग करके (ए, बी) _j , ..., z _j ), हम राज्य (i + 1, a + _j , b + b _j , ..., z + z _j ) के लिए एक संक्रमण बनाने का प्रयास कर सकते हैं और जांच सकते हैं कि क्या परिणाम इस स्थिति में सुधार करता है। महत्वपूर्ण: संक्रमण के दौरान, हम उन राज्यों में रुचि नहीं रखते हैं जहां मैं, m हूं, इसलिए, ऐसी गतिकी की कुल अवस्थाएं m ^{k + 1} से अधिक नहीं हैं, और परिणामस्वरूप असममित व्यवहार O (nm ^{k + 1} ) है। जब गतिकी की स्थिति की गणना की जाती है, तो उत्तर एक ऐसी स्थिति है जो बाधाओं को संतुष्ट करती है और उच्चतम कुल प्रासंगिकता स्कोर देती है।

कार्यान्वयन के दृष्टिकोण से, यह प्रोग्राम के काम में तेजी लाने के लिए डायनेमिक प्रोग्रामिंग की स्थिति और प्रत्येक प्रकाशन के झंडे को एक पूरे नंबर में पैक करने के लिए उपयोगी है (कोड देखें), और सूची या टपल में नहीं। यह समाधान कम मेमोरी का उपयोग करता है और आपको प्रभावी ढंग से गतिशीलता की स्थिति को अपडेट करने की अनुमति देता है।

पूर्ण समाधान कोड:

 def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score) 

बी 2। कार्य का अनुमान

शर्त

दस्तावेजों की प्रासंगिकता की डिग्री का आकलन करने के लिए, विभिन्न मशीन सीखने के तरीकों का उपयोग किया जाता है - उदाहरण के लिए, निर्णय पेड़। K-ary निर्णय ट्री में प्रत्येक नोड में एक निर्णय नियम होता है जो कुछ विशेषताओं के मूल्यों के अनुसार वस्तुओं को k वर्गों में विभाजित करता है। व्यवहार में, बाइनरी निर्णय पेड़ों का आमतौर पर उपयोग किया जाता है। अनुकूलन समस्या के सरलीकृत संस्करण पर विचार करें, जिसे k-ary निर्णय ट्री के प्रत्येक नोड में हल किया जाना चाहिए।

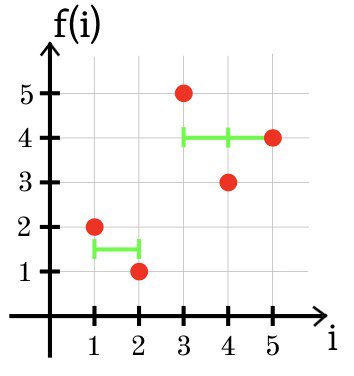
आइए मैं 1, 2, ..., n बिंदुओं पर असतत फ़ंक्शन को परिभाषित करता हूं। यह एक टुकड़ा करने योग्य निरंतर फ़ंक्शन खोजने के लिए आवश्यक है कि कांस्टेंसी के कश्मीर वर्गों से अधिक न हो, जैसे कि मूल्य एसएसई = $$$\ sum_ {i = 1} ^ n$(g (i) - f (i)) ² न्यूनतम है।

रेटिंग प्रणाली

इस कार्य के लिए परीक्षण में पाँच समूह शामिल हैं। प्रत्येक समूह के अंक केवल समूह के सभी परीक्षणों और पिछले समूहों के सभी परीक्षणों को पास करते समय दिए जाते हैं। दूसरे से शुरू होने वाले समूहों के लिए अंक प्राप्त करने के लिए शर्तों से परीक्षण पास करना आवश्यक है। कार्य के लिए कुल मिलाकर आप 100 अंक प्राप्त कर सकते हैं।

परीक्षण प्रणाली में, 1-3 परीक्षण परीक्षण स्थिति से उदाहरण हैं।

1. (10 अंक) परीक्षण 4-22: k = 1, स्थिति से किसी भी परीक्षण की आवश्यकता नहीं है
2. (20 अंक) परीक्षण 23-28: k tests 2
3. (20 अंक) का परीक्षण 29-34: k tests 3
4. (20 अंक) परीक्षण 35-40: k tests 4
5. (30 अंक) परीक्षण 41-46: कोई अतिरिक्त प्रतिबंध नहीं

निर्णय

जैसा कि आप जानते हैं, निरंतरता जो मान ₁ , f ₂ , ..., f _{n के} सेट के लिए SSE मान को न्यूनतम करता है, f _n यहाँ सूचीबद्ध मूल्यों का औसत है। इसके अलावा, जैसा कि सरल गणनाओं द्वारा सत्यापित करना आसान है, मूल्य SSE = $$$sum \ square \ मान \ - \ frac {वर्ग \ sum \ मान} {n}$।

निर्णय 10 अंक है : हम केवल फ़ंक्शन और SSE के सभी मानों के औसत को O (n) मानते हैं।

निर्णय 30 अंक का है : हम दो भागों के पहले भाग से संबंधित अंतिम बिंदु को सुलझाते हैं, एक निश्चित विभाजन के लिए हम एसएसई की गणना करते हैं और इष्टतम का चयन करते हैं। इसके अलावा, यह महत्वपूर्ण है कि मामले को अलग करना न भूलें जब कब्ज का केवल एक ही खंड होता है। कठिनाई - O (n ² )।

यह निर्णय 50 अंक का है : हम O (n ² ) के लिए विभाजन की सीमाओं को 3 खंडों में एक निश्चित विभाजन के लिए क्रमबद्ध करते हैं, हम SSE की गणना करते हैं और इष्टतम को चुनते हैं। कठिनाई - O (n ³ )।

यह निर्णय 70 अंक का है : हम उपसर्गों पर f _i के मानों के वर्ग और योगों की गणना करते हैं, इससे आप किसी भी खंड पर औसत और SSE की शीघ्र गणना कर सकेंगे। हम विभाजन की सीमाओं को O (n ³ ) के लिए निरंतरता के 4 खंडों में क्रमबद्ध करते हैं, O (1) के लिए उपसर्गों पर पूर्व-परिकलित मानों का उपयोग करके, हम SSE की गणना करते हैं। कठिनाई - O (n ³ )।

पूर्ण समाधान : डायनामिक प्रोग्रामिंग फंक्शन dp [s] [i] पर विचार करें। यह सबसे छोटा SSE मान है यदि हम s सेगमेंट का उपयोग करते हुए पहले i मानों का अनुमान लगाते हैं। तो
dp [0] [०] = ०, और मापदंडों के अन्य सभी सेटों के लिए हम इस मूल्य को और कम करने के लिए अनंत के बराबर मूल्य निर्धारित करते हैं। हम समस्या को हल करेंगे, धीरे-धीरे एस के मूल्य में वृद्धि। Dp [s] [i] की गणना कैसे करें यदि सभी छोटे s के लिए गतिशीलता मान पहले से ही गणना कर रहे हैं? यह पिछले (एस - 1) खंडों द्वारा कवर किए गए पहले बिंदुओं की संख्या को टी के लिए नामित करने के लिए पर्याप्त है, और टी के सभी मूल्यों के माध्यम से क्रमबद्ध करें, और शेष खंड का उपयोग करके शेष (आई - टी) बिंदुओं को अनुमानित करें। I बिंदुओं पर अंतिम SSE के लिए सबसे अच्छा मूल्य टी चुनना आवश्यक है। यदि हम उपसर्गों पर f _i के मानों के वर्ग और योगों की गणना करते हैं, तो यह सन्निकटन O (1) में किया जाएगा, और मूल्य dp [s] [i] की गणना O (n) में की जा सकती है। अंतिम उत्तर dp [k] [n] है। एल्गोरिथ्म की कुल जटिलता O (kn ² ) है।

पूर्ण समाधान कोड:

 n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n]) 

C. उपयोगकर्ता क्लिक की भविष्यवाणी

शर्त

एक अनुशंसा प्रणाली के लिए सबसे महत्वपूर्ण संकेतों में से एक उपयोगकर्ता व्यवहार है। , .

..

2 : (train.csv) (test.csv). , . :

— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .

.

, item, publisher, user, topic .

csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.

logloss.

150 . logloss :

$$

$$\begin{equation*} score = \begin{cases} 0 &\text{, logloss > 0.5}\\ min(150,(200 * (0.5 - logloss))^2) &\text{, logloss ≤ 0.5} \end{cases} \end{equation*}$$

logloss . 2 , logloss 4 .

, . . , (, , , ) , — , - , .

, 100 ( 150).

— CatBoost . CatBoost ( ), . , . , -: $$$(\frac{\ \ \ }{\ })$, , , , - ( ).

. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).

---

, ML- .