संवादी परत: शमूएल विनोग्राद की विधि के अनुसार तेजी से दृढ़ संकल्प

परिचय

यह लेख अंतर्निहित एल्गोरिदम का वर्णन करने वाले लेखों की एक श्रृंखला का एक निरंतरता है।
सीनेट सीपीयू पर पूर्व-प्रशिक्षित तंत्रिका नेटवर्क को लॉन्च करने के लिए एक रूपरेखा है।

पिछले लेख में, मैंने मैट्रिक्स गुणन पर आधारित विधियों का वर्णन किया था। न्यूनतम प्रयास वाले ये तरीके सैद्धांतिक अधिकतम के 80% से अधिक मामलों में प्राप्त कर सकते हैं। यह प्रतीत होता है, ठीक है, हम इसे और कहां सुधार सकते हैं? यह आप कर सकते हैं पता चला है! ऐसे गणितीय तरीके हैं जो दृढ़ संकल्प के लिए आवश्यक संचालन की संख्या को कम कर सकते हैं। हम अपने आप को इन तरीकों में से एक के साथ परिचित करेंगे, इस आलेख में विनोग्राद विधि द्वारा कन्वर्जन एल्गोरिथ्म।


शमूएल विनोग्रैड 1936.01.04 - 2019.03.25 - एक उत्कृष्ट इज़राइली और अमेरिकी कंप्यूटर वैज्ञानिक, तेज मैट्रिक्स गुणन, दृढ़ संकल्प और फूरियर रूपांतरण के लिए एल्गोरिदम के निर्माता।

थोड़ा सा गणित

हालांकि, मशीन सीखने में, एक वर्ग कोर के साथ दृढ़ संकल्प का उपयोग अक्सर किया जाता है, प्रस्तुति को सरल बनाने के लिए, हम पहले एक-आयामी मामले पर विचार करेंगे। मान लीजिए कि हमारे पास आकार की एक इनपुट-आयामी छवि है $$$1 \ times4$ :

$$

$$d = \ start {bmatrix} d_0 & d_1 & d_2 & d_3 \ end {bmatrix} ^,$$

और फिल्टर का आकार $$$1 \ टाइम्स 3$ :

$$

$$g = \ start {bmatrix} g_0 & g_1 & g_2 \ end {bmatrix} ^ T,$$

तब दृढ़ संकल्प का परिणाम होगा:

$$

$$F (2,3) = \ start {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix}।$$

इन अभिव्यक्तियों को मैट्रिक्स रूप में आसानी से लिखा जाएगा:

$$

$$F (2,3) = \ start {bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \ end {bmatrix} \ start {bmatrix} g_0 \\ g_1\ g_2 \ end {bmatrix} = \ start {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix} = \ _ शुरू {bmatrix} m_1 + m_3 \\ m_2 - m_3 - m_4 \ end {bmatrix}}। (१)$$

जहां संकेतन का उपयोग किया जाता है:

$$

$$m_1 = (d_0-d_2) g_0, \\ m_2 = (d_1 + d_2) \ frac {g_0 + g_1 + g_2} {2}, \\ m_3 = (d_2-d_1) \ frac {g_0-g_1 + g_2} {2}, \\ m_4 = (d_1-d_3) g_2।$$

पहली नज़र में, अंतिम प्रतिस्थापन कुछ हद तक बेकार दिखता है - स्पष्ट रूप से अधिक संचालन होते हैं। लेकिन भाव $$$\ frac {g_0 + g_1 + g_2} {2}$ और $$$\ frac {g_0-g_1 + g_2} {2}$ केवल एक बार गणना करने की आवश्यकता है। इसे ध्यान में रखते हुए, हमें केवल 4 गुणा संचालन करने की आवश्यकता है, जबकि मूल सूत्र में उन्हें 6 करने की आवश्यकता है।
हम अभिव्यक्ति को फिर से लिखते हैं (1):

$$

$$F (2,3) = A ^ T [(G g) \ odot (B ^ T d)], (2)$$

जहाँ $$$\ odot$ तत्व-वार गुणन को दर्शाता है, और निम्नलिखित संकेतन का भी उपयोग किया जाता है:

$$

$$B ^ T = \ start {bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 और 1 & 0 \\ 0 & 1 & 0 & 1 & -1 \ अंत { bmatrix}, (3) \\ G = \ start {bmatrix} 1 & 0 & 0 \\ \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {2} \\ \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {2} \\ 0 & 0 & 1 \ अंत {bmatrix}, (4) \\ A ^ T = \ {bmatrix} 1 और 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \ अंत {bmatrix} शुरू करें। (५)$$

अभिव्यक्ति (2) को दो-आयामी मामले में सामान्यीकृत किया जा सकता है:

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A. (6)$$

के लिए गुणन कार्यों की आवश्यक संख्या $$$F (2 \ times2,3 \ times3)$ से हटना $$$2 \ times2 \ times3 \ times3 = 36$ को $$$4 \ times4 = 16$ । इस प्रकार हम कम्प्यूटेशनल लाभ प्राप्त करते हैं $$$\ frac {36} {16} = $ 2.2$ बार। यदि आप कल्पना करते हैं, तो वास्तव में हम, छवि के प्रत्येक बिंदु के लिए अलग-अलग गणना की बजाय, हम आकार के एक ब्लॉक के लिए तुरंत गणना करेंगे। $$$2 \ times2$ :

किसी भी मामले में, खिड़की के साथ सजा के लिए $$$r \ गुना s$ और ब्लॉक आकार $$$m \ n n$ आवश्यक गुणन की संख्या होगी

$$

$$गिनती = (m + r - 1) \ n (n + s - 1), (()$$

और लाभ सूत्र द्वारा वर्णित किया गया है:

$$

$$k = \ frac {m \ टाइम्स n \ टाइम्स r \ टाइम्स s} {(m + r - 1) \ टाइम्स (n + s - 1)}। (8)$$

सीमा में, पर्याप्त रूप से बड़े के लिए $$$एम$ और $$$एन$ किसी भी दृढ़ संकल्प के लिए, एक बिंदु से गुणा का केवल 1 ऑपरेशन ही पर्याप्त है! दुर्भाग्य से, ब्लॉक आकार में वृद्धि से इनपुट ओवरहेड में तेजी से वृद्धि होती है $$$B ^ T d B$ और सप्ताहांत $$$ए ^ टी [...] एक$ छवियां, इसलिए व्यवहार में आमतौर पर ब्लॉक आकार से बड़ा उपयोग नहीं किया जाता है $$$4 \ times4$ ।

कार्यान्वयन का उदाहरण

विनोग्राद एल्गोरिथम के व्यावहारिक कार्यान्वयन के लिए, मैं सबसे सरल मामले पर विचार करना चाहूंगा - कर्नेल के साथ दृढ़ संकल्प $$$3 \ times3$ ब्लॉक के लिए $$$2 \ times2$ । प्रस्तुति को और सरल बनाने के लिए, हम यह भी मानेंगे कि इनपुट छवि का कोई पैडिंग नहीं है, और इनपुट और आउटपुट छवियों के आकार 2 के गुणक हैं।

मैट्रिक्स गुणन पर आधारित कनवल्शन कार्यान्वयन इस तरह दिखेगा:

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

जो लोग यहां पर विस्तार से समझना चाहते हैं, उन्हें मेरे पिछले लेख की ओर मुड़ना चाहिए। वर्तमान कार्यान्वयन पिछले एक से प्राप्त होता है, अगर हम डालते हैं:

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

संशोधित दृढ़ संकल्पना एल्गोरिथ्म

मैं यहां फिर से सूत्र देता हूं (6):

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

यदि आप आउटपुट इमेज साइज से स्विच करते हैं $$$2 \ times2$ मनमाने आकार की छवि के लिए, फिर हमें इसे आकार के ब्लॉक में तोड़ना होगा $$$2 \ times2$ । ऐसे प्रत्येक ब्लॉक के लिए, एक इनपुट इमेज बनाई जाएगी $$$(2 + 3 - 1) \ गुना (2 + 3 - 1) = $ 1$ मान जो 16 में शामिल किए गए हैं $$$B ^ T d B$ इनपुट चित्र आधे आकार में कम हो गए। फिर, इन 16 मैट्रिसेस में से प्रत्येक को परिवर्तित वज़न के संबंधित मैट्रिक्स से गुणा किया जाता है $$$जी जी जी ^ टी$ । 16 परिणामी मैट्रिक्स आउटपुट इमेज में परिवर्तित हो जाते हैं $$$A ^ T \ bigg [... \ bigg] A$ । नीचे यह प्रक्रिया आरेख में खींची गई है:



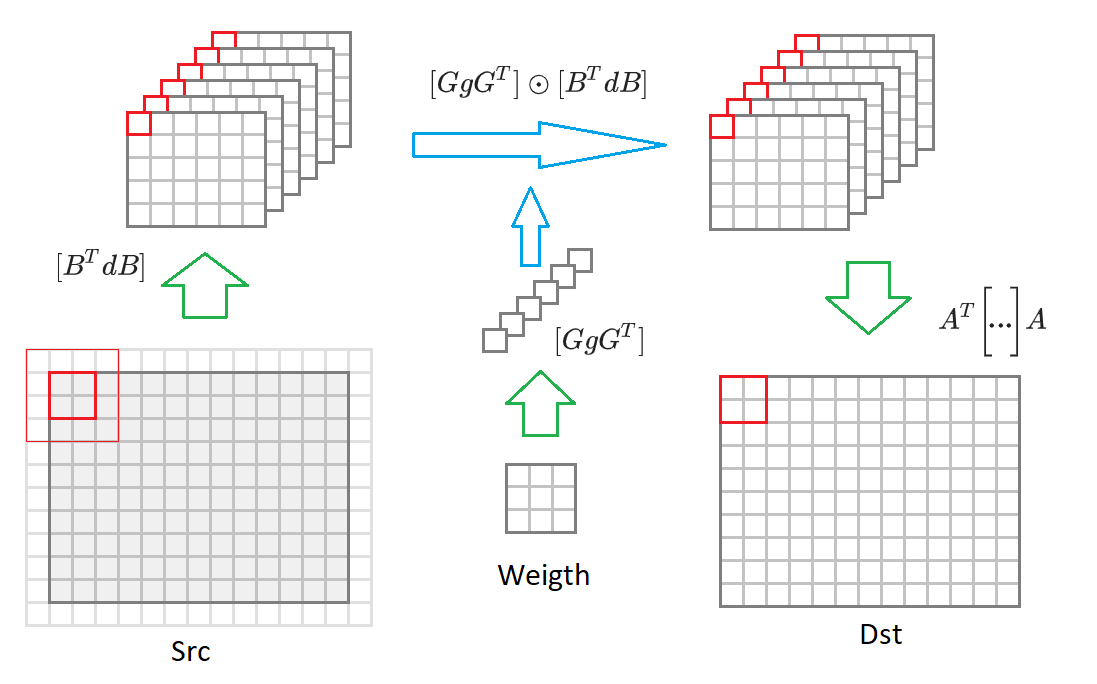
इन टिप्पणियों को देखते हुए, कन्वेंशन एल्गोरिथ्म फॉर्म लेता है:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

इनपुट और आउटपुट छवि के खाता परिवर्तनों को ध्यान में रखे बिना कितने ऑपरेशन आवश्यक हैं: ~ srcC * dstC * dstH * dstW * गिनती । अगला, हम वज़न, इनपुट और आउटपुट छवियों को परिवर्तित करने के लिए एल्गोरिदम का वर्णन करते हैं।

कन्वेन्शनल स्केल्स कन्वर्ट करें

जैसा कि अभिव्यक्ति (6) से देखा जा सकता है, निम्नलिखित परिवर्तनों को कनवल्शन वेट पर किया जाना चाहिए: $$$जी जी जी ^ टी$ मैट्रिक्स कहाँ है $$$जी$ अभिव्यक्ति में परिभाषित (4)। इस रूपांतरण का कोड इस तरह दिखेगा:

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

सौभाग्य से, इस रूपांतरण को केवल 1 बार किए जाने की आवश्यकता है। इसलिए, यह अंतिम प्रदर्शन को प्रभावित नहीं करता है।

इनपुट छवि रूपांतरण

जैसा कि अभिव्यक्ति (6) से देखा जा सकता है, इनपुट छवि पर निम्नलिखित परिवर्तन किया जाना चाहिए: $$$B ^ T d B$ मैट्रिक्स कहाँ है $$$ब ^ ट$ अभिव्यक्ति में परिभाषित (3)। इस रूपांतरण का कोड इस तरह दिखेगा:

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

इस रूपांतरण के लिए आवश्यक परिचालनों की संख्या है: ~ srcH * srcW * srcC * count ।

आउटपुट छवि रूपांतरण

जैसा कि अभिव्यक्ति (6) से देखा जा सकता है, आउटपुट इमेज पर निम्नलिखित परिवर्तन होना चाहिए: $$$ए ^ टी [...] एक$ मैट्रिक्स कहाँ है $$$ब ^ ट$ अभिव्यक्ति में परिभाषित (5)। इस रूपांतरण का कोड इस तरह दिखेगा:

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

इस रूपांतरण के लिए आवश्यक परिचालनों की संख्या है: ~ dstH * dstW * dstC * गिनती ।

व्यावहारिक कार्यान्वयन की विशेषताएं

उपरोक्त उदाहरण में, हमने आकार के एक ब्लॉक के लिए विनोह्रॉड एल्गोरिथम का वर्णन किया $$$2 \ times2$ । व्यवहार में, एल्गोरिथ्म का अधिक उन्नत संस्करण अक्सर उपयोग किया जाता है: $$$F (4 \ times4,3 \ times3)$ । इस मामले में, ब्लॉक आकार होगा $$$4 \ times4$ , और रूपांतरित मैट्रिक्स की संख्या 36 है। सूत्र (8) के अनुसार कम्प्यूटेशनल लाभ, 4 तक पहुंच जाएगा। एल्गोरिथ्म की सामान्य योजना समान है, केवल परिवर्तन एल्गोरिदम का मैट्रिक्स अलग है।

गितुब पर एक छोटी परियोजना है जो आपको इन मेट्रिसेस की गणना करने के लिए गुणांक के साथ एक मनमाने ढंग से सजा कर्नेल आकार और ब्लॉक आकार के लिए अनुमति देता है।

हमने एनसीएचडब्ल्यू छवि प्रारूप के लिए विनोग्राद एल्गोरिथ्म का एक संस्करण प्रस्तुत किया , लेकिन एल्गोरिथ्म को एनएचडब्ल्यूसी प्रारूप के लिए एक समान तरीके से लागू किया जा सकता है (मैंने पिछले लेख में इन छवि प्रारूपों के बारे में अधिक विस्तार से बात की थी ।

अतिरिक्त परिवर्तनों की उपस्थिति के बावजूद, विनोग्राद एल्गोरिथ्म में मुख्य कम्प्यूटेशनल लोड (इसके सक्षम आवेदन के साथ, निश्चित रूप से) अभी भी मैट्रिक्स गुणा पर निहित है। सौभाग्य से, यह एक मानक संचालन है और कई पुस्तकालयों में प्रभावी रूप से लागू होता है।

Vinohrad एल्गोरिथ्म के लिए विभिन्न प्लेटफार्मों के लिए अनुकूलित परिवर्तन कार्य यहां देखे जा सकते हैं ।

अंगूर एल्गोरिथ्म के पेशेवरों और विपक्ष

सबसे पहले, निश्चित रूप से, पेशेवरों:

• एल्गोरिथ्म कई बार (सबसे अधिक बार 2-3 बार) सजा की गणना को गति देने की अनुमति देता है। इस प्रकार, "सैद्धांतिक" सीमा से तेजी से सजा की गणना करना संभव है।
• एल्गोरिथ्म मानक मैट्रिक्स गुणन एल्गोरिथ्म पर इसके कार्यान्वयन में निर्भर करता है।
• इसे विभिन्न इनपुट छवि प्रारूपों के लिए लागू किया जा सकता है: एनसीएचडब्ल्यू , एनएचडब्ल्यूसी ।
• मध्यवर्ती मूल्यों को संचय करने के लिए बफर आकार मैट्रिक्स गुणन एल्गोरिथम के लिए आवश्यक से छोटा है।

अच्छी तरह से और कहाँ minuses के बिना:

• एल्गोरिथ्म प्रत्येक रूपांतरण कर्नेल आकार, साथ ही प्रत्येक ब्लॉक आकार के लिए रूपांतरण कार्यों के एक अलग कार्यान्वयन की आवश्यकता है। शायद यह मुख्य कारणों में से एक है कि यह लगभग हर जगह केवल कर्नेल के साथ दृढ़ संकल्प के लिए लागू किया गया है। $$$3 \ times3$ ।
• जैसे-जैसे ब्लॉक आकार बढ़ता है, रूपांतरण कार्यों को लागू करने की जटिलता तेजी से बढ़ती है। इसलिए, व्यावहारिक रूप से कोई ब्लॉक आकार से अधिक कार्यान्वयन नहीं हैं $$$4 \ times4$ ।
• एल्गोरिथ्म दृढ़ संकल्प मापदंडों पर सख्त प्रतिबंध लगाता है strideY = strideY = dilationY = dilationX = group = 1 । यद्यपि सैद्धांतिक रूप से, इन प्रतिबंधों का उल्लंघन होने पर एल्गोरिथ्म को लागू करना संभव है, व्यवहार में यह कम दक्षता के कारण छोटा है।
• एल्गोरिथ्म की दक्षता घट जाती है यदि छवि में इनपुट या आउटपुट चैनलों की संख्या छोटी है (यह इनपुट और आउटपुट छवियों को परिवर्तित करने की लागत के कारण है)।
• एल्गोरिथ्म की दक्षता इनपुट छवियों के छोटे आकार के लिए कम हो जाती है (इनपुट छवि से परिणामी मैट्रिक्स बहुत छोटे होते हैं, और मानक मैट्रिक्स गुणन एल्गोरिथ्म उनके लिए अप्रभावी हो जाता है)।

निष्कर्ष

विनोग्राद एल्गोरिथ्म पर आधारित दृढ़ संकल्प गणना पद्धति सरल मैट्रिक्स गुणन पर आधारित विधि की तुलना में कम्प्यूटेशनल दक्षता में काफी वृद्धि कर सकती है। दुर्भाग्य से, यह सार्वभौमिक नहीं है और इसे लागू करना काफी कठिन है। कई विशेष मामलों के लिए, तेजी से दृष्टिकोण हैं, जिसका वर्णन मैं इस श्रृंखला के अगले लेखों के लिए स्थगित करना चाहूंगा। पाठकों की प्रतिक्रिया और टिप्पणियों की प्रतीक्षा है। मुझे आशा है कि आप रुचि रखते थे!

PS यह और अन्य दृष्टिकोण सिमड लाइब्रेरी के हिस्से के रूप में कन्वेंशन फ्रेमवर्क में मेरे द्वारा कार्यान्वित किए गए हैं।
यह फ्रेमवर्क Synet को रेखांकित करता है , CPU पर पहले से प्रशिक्षित तंत्रिका नेटवर्क चलाने के लिए एक रूपरेखा।