C ++ और न्यूमेरिकल मेथड्स: लगभग न्यूटन-कोट्स इंटीग्रेशन

न्यूटन-कोट्स विधियाँ लगभग आधारित एकीकरण तकनीकों का एक संयोजन हैं:

• एकीकरण अंतराल को बराबर अंतराल में विभाजित करना;
• बहुपद द्वारा चयनित अंतराल पर इंटीग्रैंड के सन्निकटन;
• प्राप्त घुमावदार ट्रेपोज़ॉइड का कुल क्षेत्रफल ज्ञात करना।

यह लेख न्यूटन-कोट्स के कई तरीकों को कवर करेगा:

• ट्रेपेज़ॉइड विधि;
• सिम्पसन की विधि;
• रोमबर्ग विधि।

ट्रेपेज़ॉइड विधि

ट्रैपेज़ॉइड विधि माना जाने वालों में सबसे सरल है। एक उदाहरण के रूप में, निम्नलिखित अभिन्न को लें:



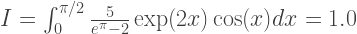
सन्निकटन की सटीकता सेगमेंट की संख्या N पर निर्भर करती है जिसमें एकीकरण अंतराल विभाजित है। इस प्रकार, अंतराल की लंबाई:





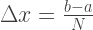
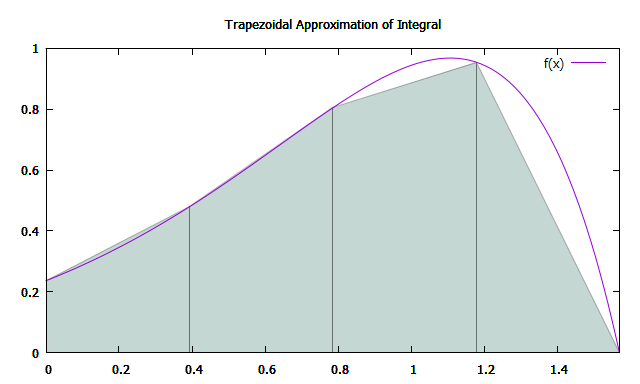
समलम्बाकार क्षेत्र की गणना सूत्र द्वारा की जा सकती है:



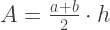
उपरोक्त सभी को सारांशित करते हुए, इंटीग्रल के अनुमानित मूल्य की गणना सूत्र द्वारा की जाती है:



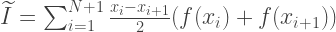
समलम्बाकार विधि द्वारा अभिन्न की गणना करने वाले फ़ंक्शन को 4 पैरामीटर लेने चाहिए:

• एकीकरण खंड की सीमाएं;
• अभिन्न कार्य;
• विभाजन के अंतराल की संख्या एन।

double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; } 

सिम्पसन विधि

सिम्पसन विधि फंक्शन x (x) के दूसरे-डिग्री प्रक्षेप बहुपद को एकीकृत करने में सम्‍मिलित करती है जिसमें a, b, और m = (a + b) / 2, parabolas p (x) होता है। सटीकता को बढ़ाने के लिए, यह एकीकरण अंतराल को N बराबर अंतरालों में विभाजित करने के लिए समझ में आता है। ट्रैपोज़ॉइड पद्धति के साथ सादृश्य द्वारा), जिनमें से प्रत्येक पर सिम्पसन विधि लागू होती है।



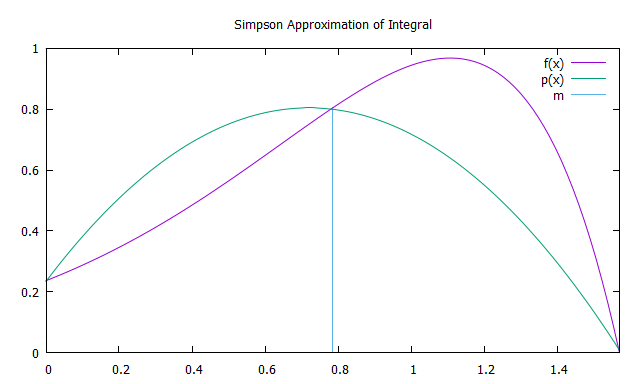
बराबर की चौड़ाई के 6 आयतों के क्षेत्रों को जोड़कर परबोला का क्षेत्र पाया जा सकता है। उनमें से पहली की ऊंचाई च (ए) के बराबर होनी चाहिए, तीसरे से पांचवें से - एफ (एम), छठे - एफ (एम) से। इस प्रकार, सिम्पसन विधि द्वारा अनुमान सूत्र द्वारा पाया जाता है:

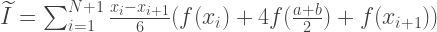
 double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double simpson_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2)); } return simpson_integral; } 

रोमबर्ग विधि

T (x) चरण x के साथ समलम्बाकार विधि द्वारा प्राप्त अभिन्न सन्निकटन है। हमें 3 ऐसे सन्निकटन मिलते हैं, जो प्रत्येक गणना के साथ चरण आकार को 2 गुना कम करते हैं।



अब हम y अक्ष के संबंध में एक परवलय सममिति का निर्माण करते हैं, जिससे अंक 0 (T) और T (1/2) से होकर गुजरते हुए x को 0 तक ले जाने के लिए प्राप्त मानों को एक्सट्रपलेट किया जा सकता है।



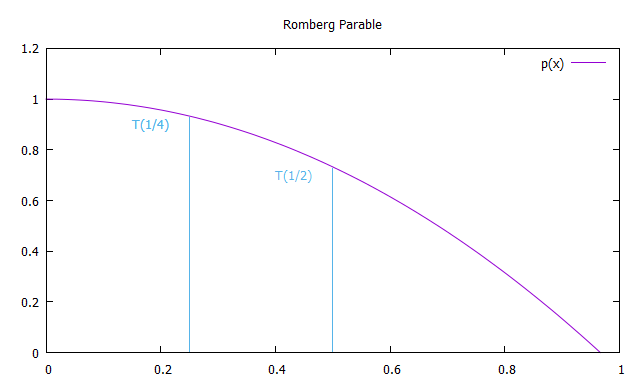
इसलिए, रोमबर्ग सन्निकटन के पहले स्तंभ R (n, 0) का प्रत्येक सदस्य समलम्बाकार विधि द्वारा प्राप्त समाधानों के बराबर है, और R (n, 1) के दूसरे स्तंभ का प्रत्येक समाधान सिम्पसन विधि के बराबर है। इस प्रकार, रोमबर्ग विधि द्वारा अनुमानित एकीकरण के सूत्र:






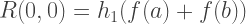
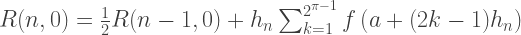
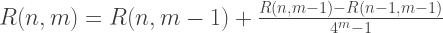
C ++ कार्यान्वयन:

 std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) { std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n)); romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f); double h = ba; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h; for(size_t rbStep = 1; rbStep <= step; rbStep++) { const double k = pow(4, rbStep); romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1); } } return romberg_integral; }