हम रैखिक प्रतिगमन समीकरण को मैट्रिक्स रूप में लाते हैं

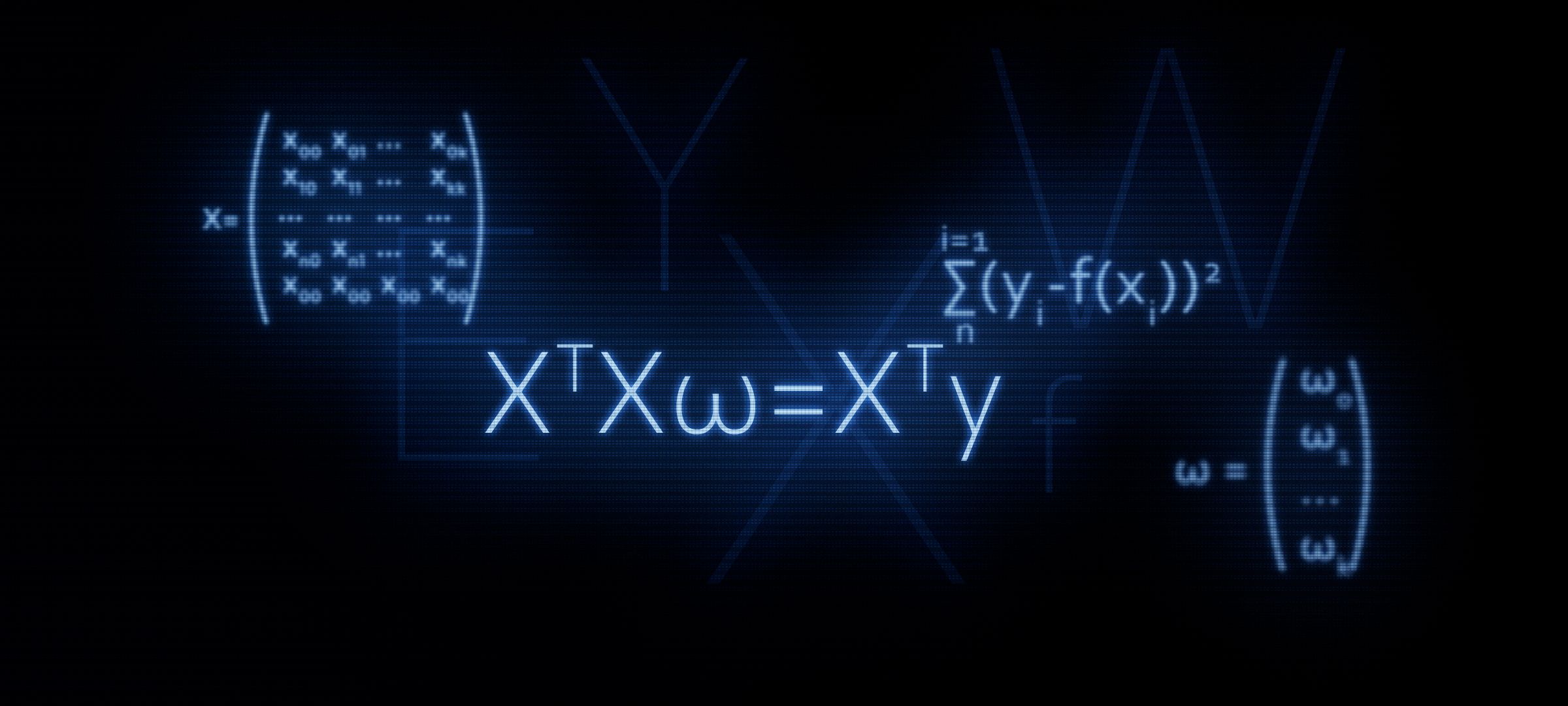
लेख का उद्देश्य नौसिखिया डेटाविंटिस्टों को सहायता प्रदान करना है। पिछले लेख में, हमने रेखीय प्रतिगमन समीकरण को हल करने के लिए उंगलियों पर तीन तरीकों की जांच की: विश्लेषणात्मक समाधान, ग्रेडिएंट डीसेंट, स्टोचैस्टिक ग्रेडिएंट डीसेंट। फिर विश्लेषणात्मक समाधान के लिए हमने सूत्र लागू किया $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ । इस लेख में, शीर्षक से निम्नानुसार, हम इस सूत्र के उपयोग को सही ठहराएंगे, या दूसरे शब्दों में, हम इसे स्वतंत्र रूप से प्राप्त करेंगे।

क्यों यह सूत्र पर ध्यान देने के लिए समझ में आता है $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ?

यह मैट्रिक्स समीकरण के साथ है कि ज्यादातर मामलों में, रैखिक प्रतिगमन के साथ परिचित होना शुरू होता है। इसी समय, सूत्र कैसे प्राप्त किया गया था, इसकी विस्तृत गणना दुर्लभ है।

उदाहरण के लिए, यैंडेक्स मशीन सीखने के पाठ्यक्रमों में, जब छात्रों को नियमितीकरण के लिए पेश किया जाता है, तो वे स्केलेर लाइब्रेरी से कार्यों का उपयोग करने का सुझाव देते हैं, जबकि एल्गोरिथ्म के मैट्रिक्स प्रतिनिधित्व के बारे में एक शब्द भी नहीं बताया गया है। यह इस समय है कि कुछ श्रोता इस मुद्दे को अधिक विस्तार से समझना चाहते हैं - तैयार कार्यों का उपयोग किए बिना कोड लिखें। और इसके लिए, हमें पहले समीकरण को नियमित रूप से मैट्रिक्स रूप में प्रस्तुत करना होगा। यह लेख उन लोगों को अनुमति देगा जो इस तरह के कौशल में महारत हासिल करना चाहते हैं। चलिए शुरू करते हैं।

प्रारंभिक स्थितियों

लक्ष्य

हमारे पास कई लक्ष्य मान हैं। उदाहरण के लिए, लक्ष्य एक परिसंपत्ति की कीमत हो सकती है: तेल, सोना, गेहूं, डॉलर, आदि। उसी समय, लक्ष्य संकेतक के कई मूल्यों से हमारा मतलब है टिप्पणियों की संख्या। इस तरह के अवलोकन हो सकते हैं, उदाहरण के लिए, वर्ष के लिए मासिक तेल की कीमतें, यानी, हमारे पास 12 लक्ष्य मान होंगे। हम संकेतन शुरू करते हैं। हम प्रत्येक लक्ष्य मान को निर्दिष्ट करते हैं $$$y_i$ । कुल हमारे पास है $$$एन$ अवलोकन, जिसका अर्थ है कि हम अपनी टिप्पणियों की कल्पना कर सकते हैं $$$y_1, y_2, y_3 ... y_n$ ।

regressors

हम मानते हैं कि ऐसे कारक हैं जो कुछ हद तक लक्ष्य संकेतक के मूल्यों की व्याख्या करते हैं। उदाहरण के लिए, डॉलर / रूबल जोड़ी की विनिमय दर तेल की कीमत, फेड दर, आदि से काफी प्रभावित होती है। ऐसे कारकों को रेजिस्टर कहा जाता है। उसी समय, लक्ष्य संकेतक के प्रत्येक मूल्य को रजिस्ट्रार के मूल्य के अनुरूप होना चाहिए, अर्थात, यदि हमारे पास 2018 में प्रत्येक महीने के लिए 12 लक्ष्य हैं, तो हमारे पास समान अवधि के लिए 12 रजिस्टर भी होने चाहिए। प्रत्येक प्रतिगामी के मूल्यों को निरूपित करें $$$x_i: x_1, x_2, x_3 ... x_n$ । हमारे मामले में है $$$k$ regressors (i.e.) $$$k$ कारक जो लक्ष्य के मूल्य को प्रभावित करते हैं)। तो हमारे रजिस्टरों को निम्न प्रकार से दर्शाया जा सकता है: 1 प्रतिगामी (उदाहरण के लिए, तेल की कीमत): $$$x_ {11}, x_ {12}, x_ {13} ... x_ {1n}$ , द्वितीय प्रतिगामी (उदाहरण के लिए, फेड दर): $$$x_ {21}, x_ {22}, x_ {23} ... x_ {2n}$ के लिए " $$$k$ वें "प्रतिगामी: $$$x_ {k1}, x_ {k2}, x_ {k3} ... x_ {kn}$

रजिस्टरों पर लक्ष्यों की निर्भरता

टारगेट डिपेंडेंस मान लें $$$y_i$ रजिस्टरों से " $$$मैं$ -th "अवलोकन फार्म के रैखिक प्रतिगमन समीकरण के माध्यम से व्यक्त किया जा सकता है:

$$

$$f (w, x_i) = w_0 + w_1 x_ {1i} + ... + w_k x_ {ki}$$

जहाँ $$$x_i$ - " $$$मैं$ वें "1 से रेजिस्टर मूल्य $$$एन$ ।

$$$k$ - 1 से रजिस्टरों की संख्या $$$k$

$$$w$ - कोणीय गुणांक जो उस राशि का प्रतिनिधित्व करते हैं जिसके द्वारा गणना करने वाले लक्ष्य सूचक औसतन बदल जाएगा जब रजिस्ट्रर बदल जाता है।

दूसरे शब्दों में, हम सभी के लिए हैं (छोड़कर) $$$w_0$ रजिस्ट्रार की) हम "हमारे" गुणांक का निर्धारण करते हैं $$$w$ , फिर रजिस्टरों के मूल्यों के गुणांक को गुणा करें " $$$मैं$ - "अवलोकन, जिसके परिणामस्वरूप हमें एक निश्चित सन्निकटन मिलता है" $$$मैं$ ध ”लक्ष्य।

इसलिए, हमें ऐसे गुणांक का चयन करने की आवश्यकता है $$$w$ जिसके लिए हमारे सन्निकटन समारोह के मूल्य $$$च (w, x_i)$ लक्ष्य के मूल्यों के जितना संभव हो उतना करीब स्थित होगा।

अनुमानित समारोह की गुणवत्ता का अनुमान

हम कम से कम वर्ग विधि द्वारा सन्निकटन समारोह की गुणवत्ता का अनुमान निर्धारित करेंगे। इस मामले में गुणवत्ता मूल्यांकन समारोह निम्नलिखित रूप लेगा:

$$

$$Err = \ sum \ limit_ {i = 1} ^ n (y_i-f (x_i)) ^ 2 \ rightarrow min$$

हमें गुणांक $ डब्ल्यू $ के ऐसे मूल्यों को चुनने की आवश्यकता है जिसके लिए मूल्य $$$एरर$ सबसे छोटा होगा।

हम समीकरण को मैट्रिक्स रूप में अनुवाद करते हैं

सदिश दृश्य

सबसे पहले, अपने जीवन को आसान बनाने के लिए, आपको रेखीय प्रतिगमन समीकरण पर ध्यान देना चाहिए और ध्यान दें कि पहला गुणांक $$$w_0$ किसी भी प्रतिगामी द्वारा गुणा नहीं। इसके अलावा, जब हम डेटा को मैट्रिक्स रूप में अनुवाद करते हैं, तो उपरोक्त परिस्थिति गंभीरता से गणना को जटिल करेगी। इस संबंध में, पहले गुणांक के लिए एक और रजिस्ट्रार पेश करना प्रस्तावित है $$$w_0$ और एक के बराबर है। या बल्कि, प्रत्येक " $$$मैं$ एकता के बराबर करने के लिए इस रजिस्ट्रार का "मूल्य" - क्योंकि जब एकता से गुणा किया जाता है, तो गणना के परिणाम के मामले में कुछ भी नहीं बदलेगा, और मैट्रिस के उत्पाद के लिए नियमों के दृष्टिकोण से, हमारी पीड़ा काफी कम हो जाएगी।

अब, थोड़ी देर के लिए, सामग्री को सरल बनाने के लिए, मान लें कि हमारे पास केवल एक है " $$$मैं$ वें "अवलोकन। फिर, रजिस्टरों के मूल्यों की कल्पना करें" $$$मैं$ एक वेक्टर के रूप में वें अवलोकन $$$\ vec {x_i}$ । वेक्टर $$$\ vec {x_i}$ आयाम है $$$(k \ टाइम्स 1)$ वह है $$$k$ पंक्तियाँ और 1 स्तंभ:

$$

$$\ vec {x_i} = \ start {pmatrix} x_ {0i} \\ x_ {1i} \\ ... \\ x_ {ki} \ end {pmatrix} \ qquad$$

वांछित गुणांक को एक वेक्टर के रूप में दर्शाया जा सकता है $$$\ vec {w}$ आयाम होना $$$(k \ टाइम्स 1)$ :

$$

$$\ vec {w} = \ start {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$$

"के लिए रेखीय प्रतिगमन समीकरण $$$मैं$ -इस "अवलोकन के रूप में ले जाएगा:

$$

$$f (w, x_i) = \ vec {x_i} ^ T \ vec {w}$$

लीनियर मॉडल का गुणवत्ता मूल्यांकन कार्य रूप लेगा:

$$

$$Err = \ sum \ limit_ {i = 1} ^ n (y_i- \ vec {x_i} ^ T \ vec {w}) ^ 2 \ rightarrow min$$

ध्यान दें कि मैट्रिक्स गुणा के नियमों के अनुसार, हमें वेक्टर को स्थानांतरित करने की आवश्यकता है $$$\ vec {x_i}$ ।

मैट्रिक्स का प्रतिनिधित्व

वैक्टर के गुणन के परिणामस्वरूप, हम संख्या प्राप्त करते हैं: $$$(1 \ गुना k) \ centerdot (k \ गुना 1) = 1 \ गुना 1$ जैसी उम्मीद थी। यह संख्या सन्निकटन है " $$$मैं$ "लक्ष्य" $$$मैं$ मैट्रिक्स रेजिस्टर $$$X$ । परिणामी मैट्रिक्स में आयाम है $$$(n \ टाइम्स k)$ :

$$$$ प्रदर्शन $ $ X = \ start {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ अंत {pmatrix} \ qquad $ $ प्रदर्शन $ $

अब रैखिक प्रतिगमन समीकरण का रूप लेगा:

$$

$$f (w, X) = X \ vec {w}$$

लक्ष्य संकेतकों के मूल्यों को नकारें (सभी $$$y_i$ ) प्रति सदिश $$$\ vec {y}$ आयामी स्वरूप $$$(n \ _ 1)$ :

$$

$$\ vec {y} = \ start {pmatrix} y_ {0} \\ y_ {1} \\ ... \\ y_ {n} \ end {pmatrix} \ qquad$$

अब हम मैट्रिक्स प्रारूप में एक रेखीय मॉडल की गुणवत्ता का आकलन करने के लिए समीकरण लिख सकते हैं:

$$

$$Err = (X \ vec {w} - \ vec {y}) ^ 2 \ rightarrow min$$

दरअसल, इस फॉर्मूले से हम अपने द्वारा ज्ञात फॉर्मूला को आगे बढ़ाते हैं $$$X ^ T X w = X ^ T y$

यह कैसे किया जाता है? कोष्ठक खोले जाते हैं, विभेदन किया जाता है, परिणामी भावों को रूपांतरित किया जाता है, आदि, और यही अब हम करने जा रहे हैं।

मैट्रिक्स परिवर्तन

कोष्ठक का विस्तार करें

$$$(X \ vec {w} - \ vec {y}) ^ 2 = (X \ vec {w} - \ vec {y}) ^ T (X \ vec {w} - \ vec {y})$

$$$= (X \ vec {w}) ^ TX \ vec {w} - \ vec {y} ^ TX \ vec {w} - (X \ vec {w}) ^ T \ vec {y} + \ vec { y} ^ T \ vec {y}$

भेदभाव के लिए एक समीकरण तैयार करें

ऐसा करने के लिए, हम कुछ परिवर्तन करते हैं। बाद की गणना में, यह हमारे लिए अधिक सुविधाजनक होगा यदि वेक्टर $$$\ vec {w} ^ $$ समीकरण में प्रत्येक कार्य की शुरुआत में प्रस्तुत किया जाएगा।

रूपांतरण १

$$$\ vec {y} ^ TX \ vec {w} = (X \ vec {w}) ^ T \ vec {y} = \ vec {w} ^ TX ^ T \ vec {y}$

यह कैसे हुआ? इस प्रश्न का उत्तर देने के लिए, गुणा गुणकों के आकारों को देखें और देखें कि आउटपुट पर हमें एक संख्या मिलती है या अन्यथा $$$कास्ट$ ।

हम मैट्रिक्स अभिव्यक्तियों के आयाम लिखते हैं।

$$$\ vec {y} ^ TX \ vec {w}: (1 \ गुना n) \ centerdot (n \ टाइम्स k) \ centerdot (k \ गुना 1) = (1 \ गुना 1) = const$

$$$(X \ vec {w}) ^ T \ vec {y}: ((n \ टाइम्स k) \ centerdot (k \ गुना 1)) ^ T \ centerdot (n \ टाइम्स 1) = (1 \ बार n) \ centerdot (n \ गुना 1) = (1 \ गुना 1) = कास्ट$

$$$\ vec {w} ^ TX ^ T \ vec {y}: (1 \ times k) \ centerdot (k \ टाइम्स n) \ centerdot (n \ गुना 1) = (1 \ गुना 1) = const$

रूपांतरण २

$$$(X \ vec {w}) ^ TX \ vec {w} = \ vec {w} ^ TX ^ TX \ vec {w}$

हम परिवर्तन 1 के समान लिखते हैं

$$$(X \ vec {w}) ^ TX \ vec {w}: ((n \ टाइम्स k) \ centerdot (k \ गुना 1)) ^ T \ centerdot (n \ टाइम्स k) \ centerdot (k \ टाइम्स 1) ) = (1 \ गुना 1) = कास्ट$

$$$\ vec {w} ^ TX ^ TX \ vec {w}: (1 \ times k) \ centerdot (k \ टाइम्स n) \ centerdot (n \ टाइम्स k) \ centerdot (k \ गुना 1) = (1 \) समय 1) = कास्ट$

आउटपुट पर, हमें एक समीकरण मिलता है जिसे हमें अलग करना है:
$$$Err = \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

हम मॉडल की गुणवत्ता का आकलन करने के कार्य को अलग करते हैं

वेक्टर द्वारा अंतर $$$\ vec {w}$ :

$$

$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}}$$

$$$(\ vec {w} ^ TX ^ TX \ vec {w}) - - (2 \ vec {w} ^ TX ^ T \ vec {y}) '+ (\ vec {y} ^ T \ vec {y }) '= 0$

$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} + 0 = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

सवाल क्यों $$$(\ vec {y} ^ T \ vec {y}) '= 0$ नहीं होना चाहिए, लेकिन अन्य दो अभिव्यक्तियों में डेरिवेटिव को निर्धारित करने के लिए संचालन, हम और अधिक विस्तार से विश्लेषण करेंगे।

भेद १

हम विभेदन प्रकट करते हैं: $$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w})} {d \ vec {w}} = 2X ^ TX \ vec {w}$

मैट्रिक्स या वेक्टर के व्युत्पन्न का निर्धारण करने के लिए, आपको यह देखने की जरूरत है कि उनके पास क्या है। हम देखते हैं:

$$$ इनलाइन $ \ vec {w} ^ T = \ start {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ इनलाइन $

$$$\ vec {w} = \ start {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad$

$$$ इनलाइन $ X ^ T = \ start {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} और x_ {11} & ... & x_ {n1}। \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ अंत {pmatrix} \ qquad $ इनलाइन $$$ $ इनलाइन $ X = \ शुरू {pmatrix} x_ {00} & x_ {01} & ... & x_ {0k} \\ x_ {10} & x_ {11} & ... & x_ {1k} \\ ... & ... & ... & ... \\ x_ {n0} & x_ {n1} & ... & x_ {nk} \ end {pmatrix} \ qquad $ इनलाइन $

मैट्रीस के उत्पाद को नकारें $$$X ^ TX$ मैट्रिक्स के माध्यम से $$$ए$ । मैट्रिक्स $$$ए$ वर्ग और इसके अलावा, यह सममित है। ये गुण आगे हमारे लिए उपयोगी होंगे, उन्हें याद रखें। मैट्रिक्स $$$ए$ आयाम है $$$(k \ टाइम्स k)$ :

$$$ इनलाइन $ A = \ start {pmatrix} a_ {00} & a_ {01} & ... और a_ {0k} \\ a_ {10} & a_ {11} & ... & a_ {1k} \\ ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad $ इनलाइन $

अब हमारा काम मैट्रिक्स द्वारा वैक्टर को सही ढंग से गुणा करना है और "दो बार दो पांच" नहीं प्राप्त करना है, इसलिए हम ध्यान केंद्रित करेंगे और बेहद सावधानी बरतेंगे।

$$$ इनलाइन $ \ vec {w} ^ TA \ vec {w} = \ start {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad \ गुना \ start {pmatrix}} \ _ {00} & a_ {01} & ... & a_ {0k} \\ a_ {10} & a_ {11} & ... और a_ {1k} \\ ... & ... & ... & \ _ \ a_ {k0} & a_ {k1} & ... & a_ {kk} \ end {pmatrix} \ qquad \ times \ start {pmatrix} w_0 \\ w_1 \\ ... \\ wk_k {अंत {pmatrix} \ qquad = $ इनलाइन $

$$$ इनलाइन $ = \ start {pmatrix} w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0} & ... & w_0a_ {0k} + w_1a_ / 1k} + ... + w_ka_ {kk} \ end {pmatrix} \ times \ start {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = $ इनलाइन $

$$$= \ start {pmatrix} (w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}) w_0 \ mkern 10mu + \ mkern 10mu + \ mkern 10mu + \ mkern 10mu (w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk}) w_k \ end {pmatat}}$

$$$= w_0 ^ 2a_ {00} + w_1a_ {10} w_0 + w_ka_ {k0} w_0 \ mkern 10mu + \ _ mkern 10mu ... \ mkern 10mu + \ _ mkern 10mu w_0a_ {0k} w_k + w_a_ 1+ {1} । + w_k ^ 2a_ {kk}$

हालाँकि, हमें एक जटिल अभिव्यक्ति मिली! वास्तव में, हमें एक संख्या मिली - एक स्केलर। और अब, पहले से ही सही मायने में, हम भेदभाव के लिए गुजरते हैं। प्रत्येक गुणांक के लिए प्राप्त अभिव्यक्ति के व्युत्पन्न को खोजना आवश्यक है $$$w_0 w_1 ... w_k$ और आउटपुट पर आयाम वेक्टर प्राप्त करें $$$(k \ टाइम्स 1)$ । बस मामले में, मैं क्रियाओं के लिए प्रक्रियाओं का वर्णन करूंगा:

1) द्वारा अंतर $$$w_o$ हमें मिलता है: $$$2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k}$

2) द्वारा अंतर $$$w_1$ हमें मिलता है: $$$w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ {k}$

3) द्वारा अंतर $$$w_k$ हमें मिलता है: $$$w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k-1) k} + a_ {k0_ w_0_ a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk}$

उत्पादन में, आकार का वादा वेक्टर $$$(k \ टाइम्स 1)$ :

$$

$$\ start {pmatrix} 2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ 02 "w_2 + ... + a_ {0k} w__ {k} \\ w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} :_2 + ... + a_ {1k} w_ {{ k} \\ ... \\ ... \\ ... \\ w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {(k-1)} a _ {(k -1) k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk} \ end {pmatrix}$$

यदि आप वेक्टर पर करीब से नज़र डालते हैं, तो आप देखेंगे कि वेक्टर के बाएं और संबंधित दाएं तत्वों को इस तरह से समूहीकृत किया जा सकता है, जिसके परिणामस्वरूप, वेक्टर को प्रस्तुत वेक्टर से अलग किया जा सकता है। $$$\ vec {w}$ आकार $$$(k \ टाइम्स 1)$ । उदाहरण के लिए $$$w_1a_ {10}$ (वेक्टर की शीर्ष पंक्ति का बायां तत्व) $$$+ a_ {01} w_1$ (वेक्टर की शीर्ष पंक्ति का सही तत्व) के रूप में प्रतिनिधित्व किया जा सकता है $$$w_1 (a_ {10} + a_ {01})$ , और $$$w_2a_ {20} + a_ {02} w_2$ - कैसे $$$w_2 (a_ {20} + a_ {02})$ आदि प्रत्येक पंक्ति पर। हम समूह:

$$

$$\ start {pmatrix} 2w_0a_ {00} + w_1 (a_ {10} + a_ {01}) + w_2 (a_ {20} + a_ {02}) + ... + w_k (a_ {k0} + a_ {) 0k}) \\ w_0 (a_ {01} + a_ {10}) + 2w_1a_ {11} + w_2 (a_ {21} + a_ {12}) + ... + w_k (a_ / k1) + a_ {1k }) \\ ... \\ ... \\ ... \\ w_0 (a_ {0k} + a_ {k0}) + w_1 (a_ {1k} + a_ {k1}) + w_2 (a_2k) } + a_ {k2}) + ... + 2w_ka_ {kk} \ end {pmatrix}$$

वेक्टर को बाहर निकालें $$$\ vec {w}$ और हम प्राप्त उत्पादन पर:

$$$ $ $ $ $ शुरू {pmatrix} 2a_ {00} & a_ {10} + a_ {01} & a_ {20} + a_ {02} & ... और a_ {k0} + a_ {0}} \\ a_ {01} + a_ {10} & 2a_ {11} & a_ {21} + a_ {12} & ... और a_ {k1} + a_ {1k} \\ ... & ... .. । & ... और ... \\ ... और ... और ... और ... और ... \\ ... और ... और ... और ... & ... । \\ a_ {0k} + a_ {k0} & a_ {1k} + a_ {k1} & a_ {2k} + a_ {k2} & ... और 2a_ {kk} \ end = इस बार "प्रारंभ" {pmatrix} w_0 \\ w_1 \\ ... \\ ... \\ ... \\ w_k \ end {pmatrix} \ qquad $ $ प्रदर्शन $ $

अब, परिणामी मैट्रिक्स पर एक नजर डालते हैं। एक मैट्रिक्स दो मैट्रिक्स का योग है $$$ए + ए ^ टी$ :

$$$$ प्रदर्शन $ $ \ _ {pmatrix} a_ {00} & a_ {01} & a_ {02} & ... & a_ {0k} \\ a_ {10} & a_ {11} & a_ {12} " ... & a_ {1k} \\ ... & ... & ... & ... & ... \\ a_ {k0} & a_ {k1} & a_ {k2} & ... & ... a_ {kk} \ end {pmatrix} + \ start {pmatrix} a_ {00} & a_ {10} & a_ {20} & ... & a_ {k0} \\ a_ {01} & a_ {11} & a_ {21} & ... & a_ {k1} \\ ... & ... & ... & ... & ... \\ a_ {0k} & a_ {1k} & a_ {2k} & ... & a_ {kk} \ end {pmatrix} \ qquad $ $ प्रदर्शन $ $

स्मरण करो कि थोड़ा पहले, हमने मैट्रिक्स की एक महत्वपूर्ण संपत्ति का उल्लेख किया $$$ए$ - यह सममित है। इस संपत्ति के आधार पर, हम विश्वास के साथ कह सकते हैं कि अभिव्यक्ति $$$ए + ए ^ टी$ बराबरी $$$2 ए$ । मैट्रिक्स-बाय-एलिमेंट उत्पाद का खुलासा करके यह सत्यापित करना आसान है $$$X ^ TX$ । हम यहां ऐसा नहीं करेंगे, जो लोग अपनी इच्छा से चेक का संचालन कर सकते हैं।

आइये अपनी अभिव्यक्ति पर वापस आते हैं। हमारे परिवर्तनों के बाद, हम इसे देखना चाहते थे:

$$

$$(A + A ^ T) \ time \ start {pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = 2A \ vec {w} = 2X - TX \ vec {w}$$

इसलिए, हमने पहले भेदभाव का सामना किया। हम दूसरी अभिव्यक्ति से गुजरते हैं।

भेद २

$$$\ frac {d (2 \ vec {w} ^ TX ^ T \ vec {y})} {d \ vec {w}} = 2X ^ T \ vec {y}$

चलो पीटा पथ के साथ चलते हैं। यह पिछले वाले की तुलना में बहुत छोटा होगा, इसलिए स्क्रीन से ज्यादा दूर न जाएं।

हम तत्व-वार वैक्टर और मैट्रिक्स प्रकट करते हैं:

$$$ इनलाइन $ \ vec {w} ^ T = \ start {pmatrix} w_0 & w_1 & ... & w_k \ end {pmatrix} \ qquad $ इनलाइन $

$$$ इनलाइन $ X ^ T = \ start {pmatrix} x_ {00} & x_ {10} & ... & x_ {n0} \\ x_ {01} और x_ {11} & ... & x_ {n1}। \\ ... & ... & ... & ... \\ x_ {0k} & x_ {1k} & ... & x_ {nk} \ अंत {pmatrix} \ qquad $ इनलाइन $

$$$\ vec {y} = \ start {pmatrix} y_0 \\ y_1 \\ ... \\ y_n \ end {pmatrix} \ qquad$

थोड़ी देर के लिए हम गणना से ड्यूस निकालते हैं - यह एक बड़ी भूमिका नहीं निभाता है, फिर हम इसे उसके स्थान पर वापस कर देंगे। मैट्रिक्स द्वारा वैक्टर को गुणा करें। सबसे पहले, हम मैट्रिक्स को गुणा करते हैं $$$X ^ T$ वेक्टर पर $$$\ vec {y}$ , यहाँ हमारे पास कोई प्रतिबंध नहीं है। आकार वेक्टर प्राप्त करें $$$(k \ टाइम्स 1)$ :

$$

$$\ start {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

निम्नलिखित क्रिया करें - वेक्टर को गुणा करें $$$\ vec {w}$ जिसके परिणामस्वरूप वेक्टर। आउटपुट पर, एक नंबर हमारा इंतजार करेगा:

$$

$$\ start {pmatrix} w_0 (x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n) + w_1 (x_ {01} y_0 + x_ / 11} y_1 + ... + x_ {n1 } y_n) \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_k (x_ {0k} y_0 + x_ {1k: y_1 + ... + x_ {nk} y_n) \ end {pmatrix} \ qquad$$

हम फिर इसे अलग करते हैं। आउटपुट में हमें एक आयाम वेक्टर मिलता है $$$(k \ टाइम्स 1)$ :

$$

$$\ start {pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

क्या यह कुछ समान है? बिलकुल ठीक! यह मैट्रिक्स का उत्पाद है। $$$X ^ T$ वेक्टर पर $$$\ vec {y}$ ।

इस प्रकार, दूसरा भेदभाव सफलतापूर्वक पूरा हुआ।

एक निष्कर्ष के बजाय

अब हम जानते हैं कि समानता कैसे आई। $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ।

अंत में, हम मुख्य सूत्रों को रूपांतरित करने का एक त्वरित तरीका बताते हैं।

कम से कम वर्ग विधि के अनुसार मॉडल की गुणवत्ता का अनुमान लगाएं:
$$$\ _ \ _ सीमाएं {{1 = 1} ^ n (y_i-f (x_i)) ^ 2 \ mkern 20mu = \ mkern 20mu \ sum \ limit_ {i = 1} ^ n (y- \-vec {x_i} ^ T) \ vec {w}) ^ 2 =$

$$$= (X \ vec {w} - \ vec {y}) ^ 2 \ mkern 20mu = \ mkern 20mu (X \ vec {w} - \ vec {y}) ^ T (X's vec {w} - \ _) vec {y}) \ mkern 20mu = \ mkern 20mu \ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + vec {y} ^ T \ vec {y}$

हम परिणामी अभिव्यक्ति को अलग करते हैं:
$$$\ frac {d (\ vec {w} ^ TX ^ TX \ vec {w} - 2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}) } {d \ vec {w}} =$$$$2X ^ TX \ vec {w} - 2X ^ T \ vec {y} = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

$$$\ _ $ गौरैया$ लेखक का पिछला काम - "हम सरल रेखीय प्रतिगमन के समीकरण को हल करते हैं"
$$$\ _ $ गौरैय$ लेखक का अगला काम है - "च्युइंग लॉजिस्टिक रिग्रेशन"

साहित्य

इंटरनेट के स्रोत:

1) habr.com/en/post/278513
2) habr.com/ru/company/ods/blog/322076
3) habr.com/en/post/307004
4) nabatchikov.com/blog/view/matrix_der

पाठ्यपुस्तकें, कार्य संग्रह:

1) उच्च गणित पर व्याख्यान नोट्स: पूर्ण पाठ्यक्रम / डी.टी. लिखित - 4th एड। - एम।: आइरिस प्रेस, 2006
2) एप्लाइड रिग्रेशन एनालिसिस / एन। ड्रेपर, जी। स्मिथ - द्वितीय संस्करण। - एम .: वित्त और सांख्यिकी, 1986 (अंग्रेजी से अनुवादित)
3) मैट्रिक्स समीकरणों को हल करने के लिए कार्य:
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html