प्लॉटली में अजीब आकर्षित करने वालों की कल्पना करना एक उत्कृष्ट कृति है

कविता एक बहुत सुंदर, अक्सर विचारशील शब्दांश है जिसे हम रोजमर्रा की जिंदगी में उपयोग नहीं करते हैं, लेकिन इस तरह से आनंद लेना पसंद करते हैं। यही बात गणित की भी कही जा सकती है। फिल्म "पाई" में, नायक गणित को "प्रकृति की भाषा" कहता है, और फिल्म "गेम्स ऑफ द माइंड" में नायक इसे "विशेष प्रकार की कला" के रूप में बोलता है। रोजमर्रा की जिंदगी में, हम इसके बारे में पूरी तरह से भूल सकते हैं।

द्वि-आयामी आयाम में भी विचित्र आकर्षित करने वालों की उपस्थिति असामान्य और आकर्षक है। प्लोटी आपको उन्हें तीन आयामों में बनाने की अनुमति देता है, और यह एक 3 डी मॉडल प्राप्त करना बहुत आसान बनाता है जिसे आप "मोड़" कर सकते हैं और जिसके माध्यम से आप "उड़" सकते हैं - "स्पर्श" की भावना।

यह सब कैसे शुरू हुआ

यह सब बहुत समय पहले शुरू हुआ था, कहीं न कहीं 2007 में विश्वविद्यालय में मैं आत्म-संगठन के सिद्धांत से परिचित हुआ था और पहली बार मैंने लॉरेंज को आकर्षित किया, एक पुस्तक में इसका काला और सफेद चित्रण। तब मुझे यह बहुत अजीब लग रहा था कि इस तरह के असामान्य प्रक्षेपवक्र के साथ कुछ चल सकता है। मेरे लिए भी अजनबी यह विचार था कि दुनिया में लगभग सभी चीजों को एक सिद्धांत द्वारा वर्णित किया जा सकता है।

सामान्य तौर पर, सब कुछ हमेशा की तरह है - मेरा विश्वदृष्टि बदल गया है, जीवन चला गया, समय बीत गया। और अब, सबसे हाल ही में, मैं एक लिंक पर आता हूं और इसे देखता हूं:


चित्र अराजक वातावरण से लिया गया है

"सुंदर।" मैंने सोचा। यह विचार कि यह सब Matplotlib में बनाया जा सकता है, लेकिन मैं पहले से ही जानता था कि कुछ भी शानदार काम नहीं करेगा। और अभी हाल ही में, सिर्फ दो हफ्ते पहले, मैं प्लॉटली से मिला और तुरंत महसूस किया कि इससे कुछ आ सकता है।

निर्माण का पहला प्रयास तुरंत विफल हो गया। यह पता चला कि "अजीब आकर्षित करने वालों की गैलरी" की कुछ छवियों के सूत्र में त्रुटियां हैं। हालांकि, गैलरी का लेखक ईमानदारी से चेतावनी देता है कि वह इस लेख के लेखक की तरह गणितज्ञ नहीं है।

एक छोटे से "google" ने इस कोड को ढूंढना संभव बना दिया, जो बेहद उपयोगी साबित हुआ और इसे माइकल टायका ने बनाया। इस अद्भुत व्यक्ति ने ब्लेंडर के लिए एक संपूर्ण प्लग-इन बनाया, जिससे आप 60 आकर्षितकर्ताओं के मॉडल (!) बना सकते हैं। वास्तव में, उन्हें एक 3 डी प्रिंटर पर मुद्रित किया जा सकता है, और यह देखते हुए कि मोम मुद्रण प्रौद्योगिकियां हैं, कांस्य में कास्टिंग के लिए एक मोल्ड प्राप्त करना काफी आसान है।

विज़ुअलाइज़ेशन कोड

खैर, एक शौकिया गणितज्ञ होने के अलावा, मैं एक शौकिया प्रोग्रामर भी हूं। इसलिए कोड की गुणवत्ता के लिए कड़ाई से न्याय न करें।

################################ ###   ### ################################ import numpy as np from scipy.integrate import odeint import plotly.graph_objects as go ################################## ###    ### ################################## #  : def LorenzMod1(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y*y - z*z + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.1 beta = 4 xi = 14 delta = 0.08 x_0, y_0, z_0 = 0, 1, 0 #      #  : tmax, n = 100, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod1, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) X, Y, Z = fT ####################### ###  ### ####################### # ,    : c = np.linspace(0, 1, n) #    : DATA = go.Scatter3d(x=X, y=Y, z=Z, line=dict(color= c, width=3, #   : # Greys,YlGnBu,Greens,YlOrRd,Bluered,RdBu, # Reds,Blues,Picnic,Rainbow,Portland,Jet, # Hot,Blackbody,Earth,Electric,Viridis,Cividis. colorscale="Cividis"), #   : mode='lines') fig = go.Figure(data=DATA) #   : fig.update_layout(width=1000, height=1000, margin=dict(r=10, l=10, b=10, t=10), #   : paper_bgcolor='rgb(0,0,0)', scene=dict(camera=dict(up=dict(x=0, y=0, z=1), eye=dict(x=0, y=1, z=1)), #   #     : aspectratio = dict(x=1, y=1, z=1), # ,    "aspectratio" aspectmode = 'manual', #  : xaxis=dict(visible=False), yaxis=dict(visible=False), zaxis=dict(visible=False) ) ) ###################### #!!  !!# ###################### fig.show() 

नतीजतन, लोरेंज मॉड 1 नामक एक अजीब आकर्षण का एक 3 डी मॉडल दिखाई देना चाहिए:


यह तुरंत ध्यान दिया जाना चाहिए कि अंतर समीकरणों की प्रणालियों को हल करने के लिए, odeint फ़ंक्शन को SciPy मॉड्यूल से चुना गया था, जो मुझे वर्किंग कोड बनाने का सबसे आसान और सबसे तेज़ तरीका लगता था। हालांकि, सभी समीकरण सामान्य यूलर विधि द्वारा हल किए जा सकते हैं।

कोड में गुणांक को इंगित करने के लिए, आदत से बाहर, मैंने LaTeX में अपनाए गए ग्रीक अक्षरों के नामों का उपयोग किया। जुपिटर नोटबुक के साथ काम करते समय, यह कभी-कभी बहुत उपयोगी होता है, क्योंकि सूत्र जल्दी से कोड बन सकते हैं, और कोड जल्दी से सूत्रों में बदल सकता है।

यदि आप पायथन पारिस्थितिकी तंत्र के लिए नए हैं, लेकिन आप चाहते हैं कि कोड को निष्पादित करने की गारंटी दी जाए, तो पायथन एनाकोंडा वितरण के नवीनतम संस्करण को स्थापित करना सबसे अच्छा है, और कॉन्डा के माध्यम से प्लॉटली पैकेज बिल्ट-इन वितरण पैकेज प्रबंधक है।

अजीब आकर्षित करने वालों की सरासर संख्या को देखते हुए, उन सभी को बनाना असंभव लगता है। इसलिए, इस लेख में मैं केवल उन लोगों के बारे में सबसे दिलचस्प बताऊंगा जिन्हें मैं बनाने में कामयाब रहा।

चेन-ली अट्रैक्टर

 #  : def ChenLee(XYZ, t, alpha, beta, delta): x, y, z = XYZ x_dt = alpha*x - y*z y_dt = beta*y + x*z z_dt = delta*z + x*y/3 return x_dt, y_dt, z_dt #     : alpha = 5 beta = -10 delta = -0.38 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 200, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChenLee, (x_0, y_0, z_0), t, args=(alpha, beta, delta)) 

चुआ आकर्षित करनेवाला

 #  : def ChuaAttractor(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ h = zeta*x + (0.5*(delta - zeta))*(np.abs(x + 1) - np.abs(x - 1)) x_dt = alpha*(-x + y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 15.6 beta = 25.58 zeta = -5/7 delta = -8/7 x_0, y_0, z_0 = 1.8, -0.7, -2.85 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

कॉउल्ट अट्रैक्टर

 #  : def Coullet(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ x_dt = y y_dt = z z_dt = alpha*x + beta*y + zeta*z + delta*x**3 return x_dt, y_dt, z_dt #     : alpha = 0.8 beta = -1.1 zeta = -0.4 delta = -1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 200, 20000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Coullet, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

द द्रास अट्रैक्टर

 #  : def DadrasAttractor(XYZ, t, rho, sigma, tau, zeta, epsilon): x, y, z = XYZ x_dt = y - rho*x + sigma*y*z y_dt = tau*y - x*z + z z_dt = zeta*x*y - epsilon*z return x_dt, y_dt, z_dt #     : rho = 3 sigma = 2.7 tau = 1.7 zeta = 2 epsilon = 9 x_0, y_0, z_0 = 0.1, 0.03, 0 #      #  : tmax, n = 220, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DadrasAttractor, (x_0, y_0, z_0), t, args=(rho, sigma, tau, zeta, epsilon)) 

दीक्वान ली अट्रैक्टर

 #  : def DequanLi(XYZ, t, alpha, beta, delta, epsilon, rho, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = rho*x + xi*y -x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 1.833 delta = 0.16 epsilon = 0.65 rho = 55 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 50, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DequanLi, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, rho, xi)) 

वित्त आकर्षित करनेवाला

 #  : def FinanceAttractor(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = (1/beta - alpha)*x + x*y + z y_dt = -beta*y - x**2 z_dt = -x - zeta*z return x_dt, y_dt, z_dt #     : alpha = 0.001 beta = 0.2 zeta = 1.1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 300, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FinanceAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

द फोर-विंग अट्रैक्टर

 #  : def FourWing(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = alpha*x + y + y*z y_dt = -x*z + y*z z_dt = -z - zeta*x*y + beta return x_dt, y_dt, z_dt #     : alpha = 5 beta = 16 zeta = 2 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 60000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FourWing, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

हेडली एट्रैक्टर

 #  : def HadleyAttractor(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -y*y - z*z - alpha*x + alpha*xi y_dt = x*y - beta*x*z - y + delta z_dt = beta*x*y + x*zz return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 4 xi = 8 delta = 1 x_0, y_0, z_0 = 0.39, -1, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HadleyAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

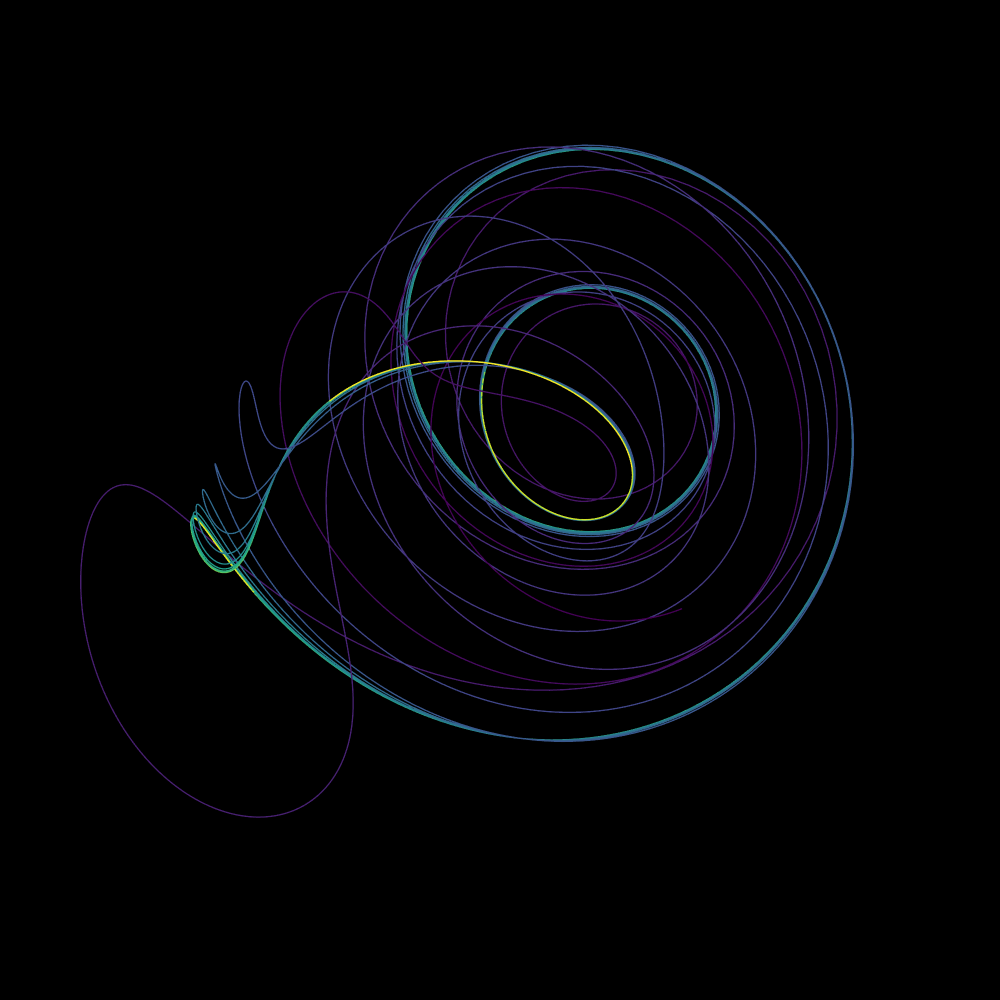
हलवोरसेन अट्रैक्टर

 #  : def HalvorsenAttractor(XYZ, t, alpha): x, y, z = XYZ x_dt = -alpha*x - 4*y - 4*z - y*y y_dt = -alpha*y - 4*z - 4*x - z*z z_dt = -alpha*z - 4*x - 4*y - x*x return x_dt, y_dt, z_dt #     : alpha = 1.4 x_0, y_0, z_0 = -5, 0, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HalvorsenAttractor, (x_0, y_0, z_0), t, args=(alpha,)) 

लियू-चेन अट्रैक्टर

 #  : def LiuChen(XYZ, t, alpha, beta, sigma, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*y + beta*x + sigma*y*z y_dt = delta*y - z + epsilon*x*z z_dt = xi*z - x*y return x_dt, y_dt, z_dt #     : alpha = 2.4 beta = -3.75 sigma = 14 delta = -11 epsilon = 4 xi = 5.58 x_0, y_0, z_0 = 1, 3, 5 #      #  : tmax, n = 55, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LiuChen, (x_0, y_0, z_0), t, args=(alpha, beta, sigma, delta, epsilon, xi)) 

लोरेंज मॉड 2 अट्रैक्टर

 #  : def LorenzMod2(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y**2 -z**2 + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.9 beta = 5 xi = 9.9 delta = 1 x_0, y_0, z_0 = 5, 5, 5 #      #  : tmax, n = 50, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod2, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

संशोधित चुआ अराजक आकर्षण

 #  : def ChuaModified(XYZ, t, alpha, beta, gamma, delta, zeta): x, y, z = XYZ h = -delta*np.sin((np.pi*x)/(2*gamma)) x_dt = alpha*(y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 10.82 beta = 14.286 gamma = 1.3 delta = 0.11 zeta = 7 x_0, y_0, z_0 = 1, 1, 0 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaModified, (x_0, y_0, z_0), t, args=(alpha, beta, gamma, delta, zeta)) 

द न्यूटन लीपनिक अट्रैक्टर

 #  : def NewtonLeipnik(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -alpha*x + y + 10*y*z y_dt = -x - 0.4*y + 5*x*z z_dt = beta*z - 5*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.175 x_0, y_0, z_0 = 0.349, 0, -0.16 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NewtonLeipnik, (x_0, y_0, z_0), t, args=(alpha, beta)) 

नाक-हूवर आकर्षण

 #  : def NoseHoover(XYZ, t, alpha): x, y, z = XYZ x_dt = y y_dt = -x + y*z z_dt = alpha - y*y return x_dt, y_dt, z_dt #     : alpha = 1.5 x_0, y_0, z_0 = 1, 0, 0 #      #  : tmax, n = 150, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NoseHoover, (x_0, y_0, z_0), t, args=(alpha,)) 

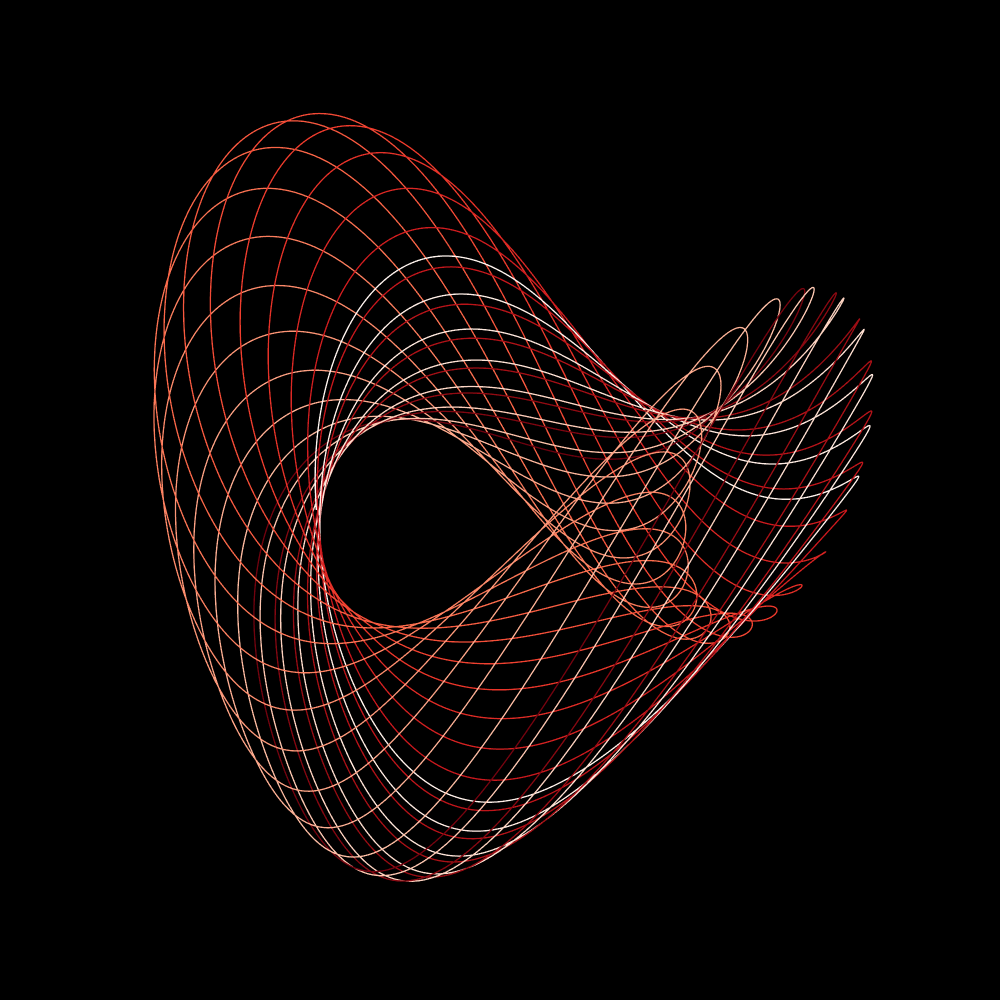
द रोस्लर अट्रैक्टर

 #  : def Roessler(XYZ, t, alpha, beta, sigma): x, y, z = XYZ x_dt = -(y + z) y_dt = x + alpha*y z_dt = beta + z*(x - sigma) return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 0.2 sigma = 5.7 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Roessler, (x_0, y_0, z_0), t, args=(alpha, beta, sigma)) 

द सकराय अट्रैक्टर

 #  : def SakaryaAttractor(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -x + y + y*z y_dt = -x - y + alpha*x*z z_dt = z - beta*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.3 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(SakaryaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta)) 

थॉमस अट्रैक्टर

 #  : def Thomas(XYZ, t, beta): x, y, z = XYZ x_dt = -beta*x + np.sin(y) y_dt = -beta*y + np.sin(z) z_dt = -beta*z + np.sin(x) return x_dt, y_dt, z_dt #     : beta = 0.19 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 185, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Thomas, (x_0, y_0, z_0), t, args=(beta,)) 

तीन-स्क्रॉल एकीकृत अराजक प्रणाली आकर्षण (TSUCS1)

 #  : def TSUCS1(XYZ, t, alpha, beta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = xi*y - x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 0.833 delta = 0.5 epsilon = 0.65 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 70, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(TSUCS1, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, xi)) 

वांग-सूरज आकर्षित करने वाला

 #  : def WangSunAttractor(XYZ, t, alpha, beta, zeta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*x + zeta*y*z y_dt = beta*x + delta*y - x*z z_dt = epsilon*z + xi*x*y return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = -0.01 zeta = 1 delta = -0.4 epsilon = -1 xi = -1 x_0, y_0, z_0 = 0.5, 0.1, 0.1 #      #  : tmax, n = 500, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(WangSunAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta, epsilon, xi)) 

निष्कर्ष में

अग्नि, जल, पृथ्वी, आकाश, सूर्य, चंद्रमा, तारे - ये सभी सबसे प्राचीन काव्य निबंध हैं। बहुत बार मैं गणित में कुछ समान रूप से सुंदर खोजने का प्रबंधन करता हूं। लेकिन बहुत बार मुझे यह भी समझ में नहीं आता है कि गणितीय भाषा और साधारण भाषा में इस सब के बारे में कैसे बात करें। मैं समझ नहीं पाया, लेकिन मैं सीखना चाहता हूं।

लेकिन मुझे जो 100% का एहसास हुआ, वह यह है कि आधुनिक विज़ुअलाइज़ेशन टूल आपके दृष्टिकोण को व्यक्त करने का एक शानदार अवसर प्रदान करते हैं कि आप अभी क्या कर रहे हैं, यह दिखाने का अवसर कि यह आपके लिए कितना महत्वपूर्ण है और आप कितने दिलचस्प हैं। यह सब बिना शब्दों के करें।