मैंने एक बार
एक लेख लिखा था, जिसमें मैंने एक तंत्रिका नेटवर्क के विकास का एक सरल गणितीय मॉडल और इसके चयन को संख्या 2 और सुनहरे अनुपात के साथ संख्या प्रणाली में संख्याओं को जोड़ने की क्षमता के लिए वर्णित किया था, और यह पता चला कि सुनहरा अनुपात बेहतर काम करता है। इसलिए, मेरा पहला अनुभव बहुत बुरा निकला, क्योंकि मैंने इस तथ्य से संबंधित कई महत्वपूर्ण बारीकियों को ध्यान में नहीं रखा था कि त्रुटि को न्यूरॉन के लिए ध्यान में नहीं रखा जाना चाहिए, लेकिन थोड़ी सी जानकारी के लिए, इसलिए मैंने अपने प्रयोग में सुधार करने का फैसला किया, और कुछ और परिचय दिए। समायोजन।
- मैंने 15 सिस्टम (सैंपल सैंपल) और 1000 (टेस्ट सैंपल) सैंपल के 100 जोड़े को समान रूप से वितरित बेस के साथ दो पहले से ज्ञात ठिकानों के बजाय 1.2 से 2 के आधार पर जांचने का फैसला किया।
- मैंने आधार से स्वर्ण अनुपात तक की दूरी से न केवल एक रेखीय प्रतिगमन बनाया, बल्कि आधार से ही, वेक्टर में निर्देशांक की संख्या और प्रतिक्रिया वेक्टर में समन्वय के औसत मूल्य, आधार पर त्रुटि के गैर-रैखिकता को ध्यान में रखना था।
- मैंने Kolmogorov-Smirnov मानदंड, ANOV द्वारा सामान्यता के लिए कुछ नमूनों की भी जाँच की, लेकिन इन मानदंडों से पता चला कि नमूने सबसे अधिक संभावित रूप से गौसियन से विचलित होते हैं, इसलिए मैंने सामान्य के बजाय एक भारित रेखीय प्रतिगमन बनाने का निर्णय लिया। हालांकि, एनोवा, हालांकि इसने एफ को पहले की तुलना में थोड़ा कम दिखाया (800-900 के बजाय 700-800 के क्षेत्र में), लेकिन फिर भी परिणाम सांख्यिकीय रूप से अधिक महत्वपूर्ण बना रहा, जिसका मतलब है कि अधिक परीक्षण किए जाने चाहिए। इन परीक्षणों के रूप में, मैंने प्रतिगमन अवशेषों और सामान्य QQ के वितरण घनत्व का एक हिस्टोग्राम लिया - इन अवशेषों के वितरण समारोह का एक ग्राफ।
ये दो रेखांकन हैं:
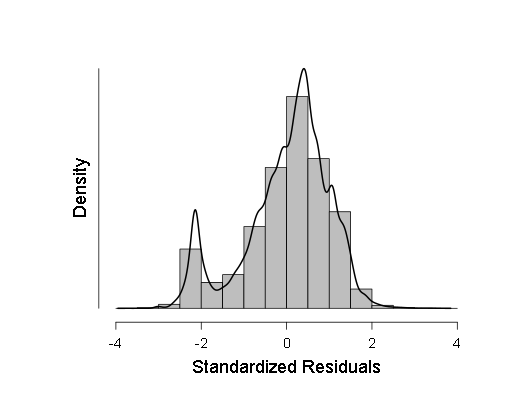
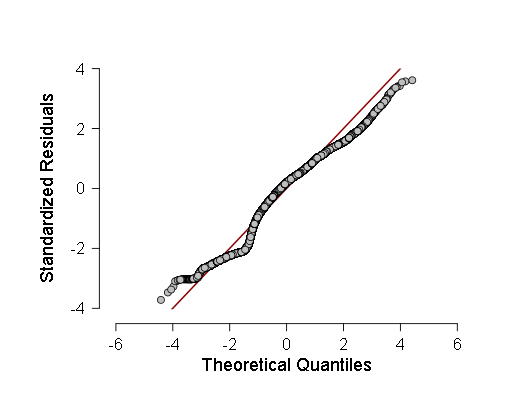
जैसा कि देखा जा सकता है, हालांकि अवशेषों के वितरण में सामान्य वितरण से विचलन सांख्यिकीय रूप से महत्वपूर्ण है (और बाईं तरफ, यहां तक कि हिस्टोग्राम पर एक छोटा सा दूसरा मोड दिखाई देता है), वास्तव में यह गौसियन के बहुत करीब है, इसलिए, इस रैखिक प्रतिगमन पर भरोसा करना संभव है (सावधानी और बड़े आत्मविश्वास अंतराल के साथ)। ।
अब मैं उनके बारे में तंत्रिका नेटवर्क के परीक्षण के लिए नमूने कैसे तैयार करता हूं।
यहाँ नमूने उत्पन्न करने के लिए कोड है: और यहाँ हैडर फ़ाइल कोड है: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);// x a t n . void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; // t . for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;// , . while ((l<=k-1)&&(m<nk-1)) // x a ( ), { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=yb; (*(t+kl))=true; } } else { b=1; m=0; while ((b>y)&&(m<nk-1)) { b=b/a; m++; } if ((b<y)||(m<nk-1)) { y=yb; (*(t+k+m))=true; } } } return; }
मैंने तंत्रिका नेटवर्क का पूरा कोड पोस्ट करने का भी फैसला किया है: इसके बाद, आइए बात करते हैं कि मैंने भारित रैखिक प्रतिगमन का संचालन कैसे किया। ऐसा करने के लिए, मैंने बस तंत्रिका नेटवर्क के परिणामों के मानक विचलन की गणना की, और फिर यूनिट को उनमें विभाजित किया।
यहाँ कार्यक्रम का स्रोत कोड है जिसके साथ मैंने यह किया है: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");// . double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; };
इसके बाद, मैंने परिणामी भार को तालिका में जोड़ दिया, जहां मैंने कार्यक्रम के परिणामस्वरूप प्राप्त सभी डेटा को कम कर दिया, साथ ही प्रतिगमन की गणना करने के लिए चर के मूल्यों और फिर इसे JASP में गणना की। यहाँ परिणाम हैं:
परिणाम
रैखिक प्रतिगमन
अगला, मेरे पास मानकीकृत प्रतिगमन अवशेषों के वितरण घनत्व का एक हिस्टोग्राम है:

साथ ही मानकीकृत प्रतिगमन अवशेषों के सामान्य मात्रात्मक-मात्रात्मक ग्राफ:

तब मैंने चर के लिए अपने पाठ्यक्रम में प्राप्त प्रतिगमन गुणांक के औसत मूल्यों को लागू किया, और संख्या प्रणाली के आधार से त्रुटि फ़ंक्शन के सबसे संभावित न्यूनतम (कितना इन इन चर से संबंधित है) का पता लगाने के लिए अपने सांख्यिकीय विश्लेषण को अंजाम दिया, जिसमें फ़र्मेट की लेम्मा, बेयस प्रमेय और लैगरेंज प्रमेय का उपयोग किया गया। निम्नानुसार है:
तथ्य यह है कि नमूना में संख्या प्रणाली के आधारों का वितरण स्पष्ट रूप से एक समान था, इसलिए, यदि अंतराल (1,2; 2) में एक निश्चित आधार औसत-वर्ग त्रुटि है, तो, फ़र्मेट के लेम्मा द्वारा, इसमें शून्य व्युत्पन्न होगा, फिर मानों की संभावना घनत्व; फ़ंक्शन अनंत होगा।
अब मैंने बेयस प्रमेय को कैसे लागू किया, इसके बारे में। मैंने बीटा वितरण के विश्वास अंतराल की गणना की (यह n "सफलताओं" और m "विफलताओं" की संभावना घनत्व के साथ प्रयोग में "सफलता" की संभावना वितरण है
) वितरण फ़ंक्शन के मान (यह संभावना है कि गणना की गई त्रुटियों का यादृच्छिक चर तर्क से बड़ा नहीं है), इस तथ्य पर आधारित है कि यदि यादृच्छिक चर तर्क से बड़ा नहीं है, तो यह "सफलता" है, और यदि यह अधिक है, तो "विफलता"। फिर, बायेसियन प्रमेय का उपयोग करते हुए, हम गणना की गई त्रुटियों के वितरण फ़ंक्शन के बीटा वितरण को लागू करते हैं, और प्रत्येक गणना की गई त्रुटि में 99% के अपने [वितरण समारोह] विश्वास अंतराल की गणना करते हैं।
हम लग्र प्रमेय पास करते हैं। लैग्रेंज प्रमेय में कहा गया है कि यदि फ़ंक्शन f (x) अंतराल [a; b] पर लगातार भिन्न होता है, तो कम से कम इस अंतराल के एक बिंदु पर इसका व्युत्पन्न बराबर होता है।
। मैं इस प्रमेय को कैसे लागू करता हूं: तथ्य यह है कि संभाव्यता घनत्व वितरण फ़ंक्शन का व्युत्पन्न है, इसलिए मैं उन लोगों के बीच अधिकतम मूल्य लेता हूं जो इसे न्यूनतम अंतराल से शेष त्रुटियों के लिए कुछ अंतरालों में लेते हैं। फिर मैं निम्न सूत्र का उपयोग करके 98% (बोन्फ्रोनी सुधार का उपयोग करके) ऐसे मूल्यों के विश्वास अंतराल की गणना करता हूं:
[\ frac {F_1 (x_i) -F_2 (x_1)} {x_i-x_1}; \ frac {F_2 (x_i) -F_1 (x_1)} {x_i-x_1}}
जहां एफ 1 वितरण फ़ंक्शन के लिए विश्वास अंतराल का बायां छोर है, और एफ 2 दाईं ओर है, x_i, x_1 वितरण फ़ंक्शन के तर्क के रूप में गणना की गई त्रुटियां हैं। अगला, कार्यक्रम सबसे बड़े बाएं छोर और सबसे बड़े दाएं छोर के साथ अंतराल की खोज करता है (ताकि अंतराल में मूल्य अधिकतम हो), और फिर इस अंतराल में गणना की गई त्रुटियों के अनुरूप होने वाले ठिकानों में अधिकतम और न्यूनतम की तलाश करता है। ये अधिकतम और न्यूनतम नीचे से त्रुटि फ़ंक्शन के तर्क हैं, जिसके बीच 98% की संभावना के साथ फ़ंक्शन का न्यूनतम निहित है।
यहाँ उस कार्यक्रम का कोड है जिसे मैंने स्पष्टीकरण के साथ इस सांख्यिकीय विश्लेषण का संचालन किया है: और यहाँ हैडर फ़ाइल कोड है: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);// - n "" m "", " " " " , : double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);// - ( ): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,mi,x); } c = (double) c/(n+m+2); return c; } // : void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }
यहाँ इस कार्यक्रम के काम का परिणाम है जब मैंने उसे संख्या प्रणाली और प्रतिगमन के परिणामों की नींव दी:
x (- [1.501815; 1.663988] y (- [0.815782; 0.816937]
(इस मामले में "(-") सेट सिद्धांत से संकेत "संबंधित" का सिर्फ एक अंकन है, और वर्ग कोष्ठक अंतराल का संकेत देते हैं।)
इस प्रकार, यह मुझे पता चला है कि सूचना के प्रसारण में त्रुटियों की कम से कम संख्या के संदर्भ में संख्या प्रणाली का सबसे अच्छा आधार 1.501815 से लेकर 1.663988 तक है, अर्थात्, स्वर्ण अनुपात पूरी तरह से इसमें आता है। सही है, मैंने विभिन्न संख्या प्रणालियों में जानकारी की मात्रा की गणना करते समय न्यूनतम और एक की गणना करते समय एक धारणा बनाई: सबसे पहले, मैंने यह माना कि आधार से त्रुटि फ़ंक्शन लगातार भिन्न होता है, और दूसरी बात, यह कि एकरूपता वितरित संख्या की संभावना 1 से है। 2 से 2 में एक विशिष्ट अंक में नंबर एक होगा, यह दशमलव बिंदु के बाद कुछ अंकों के बाद लगभग समान होगा।
यदि मैंने कुछ पूरी तरह से गलत किया है, या बस गलत है, तो मैं आलोचना और सुझावों के लिए खुला हूं। मुझे उम्मीद है कि यह प्रयास अधिक सफल रहा।
युपीडी। मैंने "विशुद्ध रूप से वैज्ञानिक" भाग में कुछ स्थानों को स्पष्ट करने के लिए लेख को दो बार संपादित किया, और कोड को स्वरूपित भी किया।
UPD2। एक व्यक्ति के साथ परामर्श करने के बाद जो जैव सूचना विज्ञान (आईपीबीआई आरएएस में एफबीबी एमएसयू स्नातकोत्तर अध्ययन के एक स्नातक) को समझता है, यह शब्द》 मस्तिष्क》 को ural तंत्रिका नेटवर्क 《के साथ बदलने का निर्णय लिया गया था, क्योंकि वे बहुत हैं।