जियोडेसिक गुंबद। डिवाइस और गणना के मेरे अनुभव के बारे में

शायद भूगर्भिक गुंबदों को कुछ असामान्य या नया कहना मुश्किल है। इस लेख में, मैं इन डिजाइनों के बारे में सामान्य रूप से, उनकी संरचना के बारे में, और यह भी दिखाऊंगा कि कैसे मैंने इस विषय पर कुछ सोचा। कोड भी होगा।



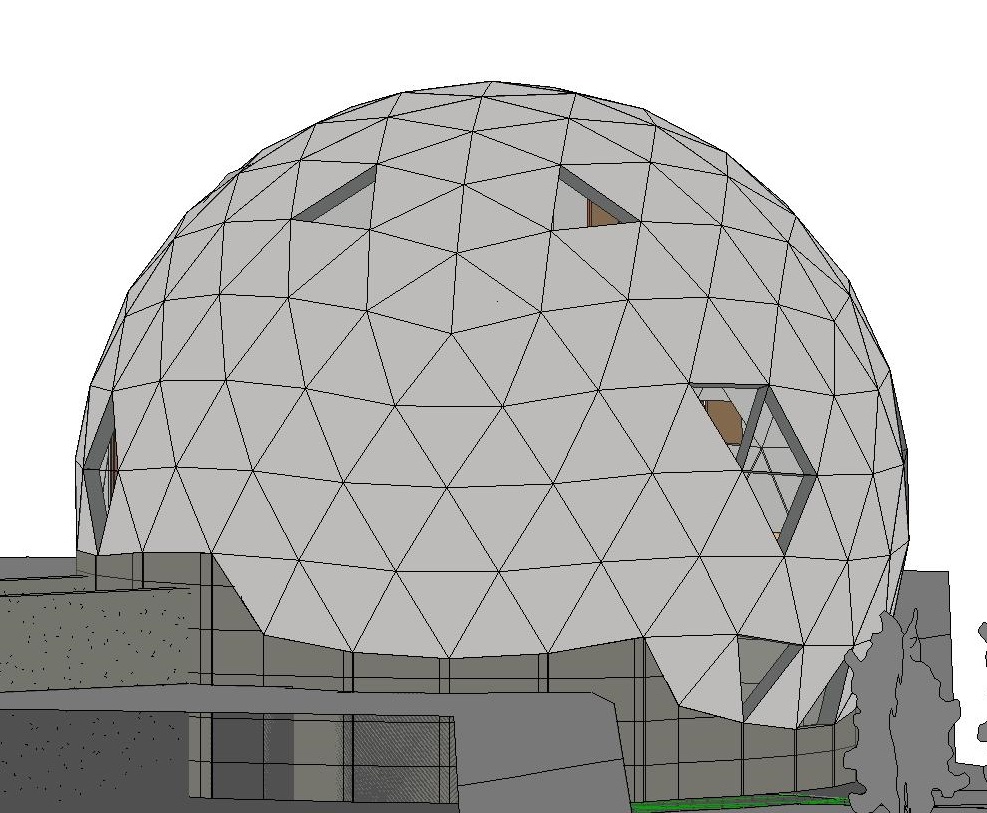
मैं विकिपीडिया को उद्धृत नहीं करूंगा। मैंने अपने घर के रूप में गुंबद को क्यों चुना?

• एक समान मात्रा के साथ, गोले का सतह क्षेत्र किसी भी अन्य आकार की तुलना में कम होगा। यह ऑपरेशन के दौरान सामग्री की खपत और ऊर्जा खपत दोनों को सकारात्मक रूप से प्रभावित करता है।
• मुझे पसंद है कि क्षेत्र कैसा दिखता है।
• यह एक दिलचस्प इंजीनियरिंग परियोजना है, एक अर्थ में, एक चुनौती भी। यह कठिन, कठिन और इसलिए मज़ेदार है!
  

कैसे इन जियोडेसिक क्षेत्रों को सामान्य रूप से व्यवस्थित किया जाता है? पहली नज़र में, ऐसा लगता है कि यह किनारों के किसी प्रकार का इंटरव्यू है और सिस्टम को पकड़ना मुश्किल है। हम यह पता लगाने की कोशिश करेंगे।

ऐसी संरचनाओं का आधार icosahedron या octahedron है। सामान्य तौर पर, एक नियमित पॉलीहेड्रॉन।
मेरे मामले में, यह वास्तव में इकोसैड्रोन था और इसका उपयोग अधिक बार किया जाता है। अगला, हम एक चेहरा लेते हैं और इसे कई त्रिभुजों के साथ प्रतिस्थापित करते हैं, जिनके कोने एक गोले पर स्थित होते हैं जिसका केंद्र इकोसाहेड्रोन के केंद्र के साथ मेल खाता है। यह बहुत अच्छा नहीं लगता है। पचाते हैं।

एक अद्भुत कैलकुलेटर है www.acidome.ru जो आपको वास्तविक समय में एक सर्वेक्षक को मोड़ने की अनुमति देता है। बेस के रूप में आइकोसैहेड्रोन लें, आवृत्ति को 1, क्षेत्र के भाग 1/1 पर सेट करें।



यह हमारा मुख्य icosahedron है। फ़्रिक्वेंसी है कि हम कितने भागों को तोड़ेंगे जो आइकोसैहेड्रॉन के प्रत्येक किनारे को तोड़ देगा। हमने 3.4, 5 सेट किया और कुछ भी स्पष्ट नहीं हुआ। छत मोड पर जाएं और पेंटागन की तलाश करें। उन जगहों पर जहां हमारे पास icosahedron का शीर्ष है - एक पेंटागन होगा। तीन पेंटागन के बीच इकोसैहेड्रॉन का चेहरा है।



यदि आप ध्यान से जियोडेसिक को देखते हैं और जानते हैं कि क्या देखना है (आमतौर पर एक पेंटागन), तो संरचना की नियमितता दिखाई देती है। मॉन्ट्रियल में बायोस्फीयर पर, उचित परिश्रम के साथ, आप पेंटागन पा सकते हैं और आवृत्ति की गणना कर सकते हैं। हमारी आवृत्ति दो पेंटागन के बीच किनारों की संख्या के बराबर है।

"बड़ा" खुद को त्रिकोण बनाता है, इकोसैहेड्रोन के शीर्ष पर कोने के साथ, एक संरचना भी होती है। अम्लीय छत पर, यह रंग में दिखाई देता है। त्रिकोण "बड़े" त्रिकोण के केंद्र के संबंध में सममित रूप से स्थित हैं। उनके प्रकारों की संख्या त्रिकोणों की कुल संख्या से कम है। 5 अद्वितीय त्रिकोण 9 की आवृत्ति के मामले में।



एक घर को डिजाइन करने की प्रक्रिया में, मुझे डायनामो में एक गोले के निर्माण के कार्य के साथ सामना करना पड़ा। यह एक उपकरण है जो आपको जटिल रूपों के साथ काम करने के लिए ऑटोडेस्क रेविट सिखाता है। ऐसा दृश्य प्रोग्रामिंग वातावरण।
Googling, मुझे यहां तक ​​कि एक स्केच भी मिला जिसने डायनमो में एक जियोडेसिक क्षेत्र का निर्माण किया। उन्होंने क्षेत्र का निर्माण किया, लेकिन वह नहीं।

ये रही बात। जब हम इकोसाहेड्रॉन के एक किनारे को लेते हैं और इसे छोटे त्रिकोणों में विभाजित करते हैं - यह कई तरीकों से किया जा सकता है। अम्लीयता में, "विभाजन विधि" स्विच इसके लिए जिम्मेदार है।

पाया स्केच ने बराबर जीवा विधि का उपयोग करके गोले का निर्माण किया। इसका क्या मतलब है? हम icosahedron का एक बड़ा त्रिकोण लेते हैं, इसके प्रत्येक किनारों को हमारी ज़रूरत के भागों में विभाजित करते हैं, किनारों पर बिंदुओं को एक दूसरे से जोड़ते हैं और त्रिकोण का एक फ्लैट ग्रिड प्राप्त करते हैं। फिर हम इस ग्रिड को गोले पर रखते हैं। सब कुछ ठीक होगा, लेकिन ये त्रिकोण खुद आकार में काफी अलग हैं। सबसे बढ़कर मध्य। यह समझ में आता है, "बड़े" त्रिभुज का केंद्र गोला से हमारी अधिकतम दूरी पर है। यह खराब है, क्योंकि इस मामले में सामग्री की खपत को अनुकूलित करना अधिक कठिन है। अधिक बर्बादी होगी।

बंटवारे की एक और विधि (बराबर चाप के साथ) मानती है कि हम आर्क के "बड़े" त्रिकोण के शीर्ष पर बनाते हैं और पहले से ही उन्हें समान भागों में विभाजित करते हैं। दृष्टिकोण अलग है, एक साधारण प्रक्षेपण नहीं कर सकता है।

स्केच फिट नहीं था। मैंने इसे ठीक करने की कोशिश की और अंत में मुझे अपने सिर के साथ इस व्यवसाय में गोता लगाना पड़ा।

जैसा कि यह निकला, दृश्य वातावरण के अलावा, डायनमो ने अंतर्निहित पायथन बनाया है। मैंने पहले इस भाषा का सामना नहीं किया है, लेकिन हमारी भाषा कहाँ गायब नहीं हुई है? अंत में, यह सिर्फ एक उपकरण है।

फिर कोड के टुकड़े होंगे, कृपया ध्यान दें कि यह अजगर में मेरी नमस्ते दुनिया है, और लक्ष्य सबसे प्रभावी और कुशल समाधान का निर्माण नहीं था, लेकिन सही क्षेत्र का निर्माण करना था।

बराबर चाप की विधि।

हम आइकोसैहेड्रोन के चेहरे में से एक लेते हैं और इस त्रिकोण के कोनों से आर्क का निर्माण करते हैं।

for k, edge in enumerate(curves): #   arc = Arc.ByCenterPointStartPointEndPoint(sphere_center, edge.EndPoint, edge.StartPoint) #   ,    result_points.append(edge.EndPoint) result_points.append(edge.StartPoint) #    "",       if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, edge.StartPoint, edge.EndPoint) #      arc_points = Arc.PointsAtEqualSegmentLength(arc, n) else: arc_points = list(reversed(Arc.PointsAtEqualSegmentLength(arc, n))) #     for p in arc_points: result_points.append(p) 

फिर हम आर्क्स को समान भागों में विभाजित करते हैं और अंक को नए आर्क्स के साथ आर्क पर जोड़ते हैं। सभी आर्क्स का एक केंद्र है - गोले का केंद्र। अंक सभी के साथ नहीं, बल्कि एक ही नाम से जुड़े होते हैं। तस्वीर में यह कोड की तुलना में सरल दिखता है।

 for edge_index, point_list in enumerate(points): edge_arcs = [] for point_index, point in enumerate(point_list): next_edge_index = edge_index + 1 if len(points) == next_edge_index: next_edge_index = 0 end_point_index = n - point_index - 2 arc = Arc.ByCenterPointStartPointEndPoint(center_point, points[next_edge_index][end_point_index], point) if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, point, points[next_edge_index][end_point_index]) arc_points_count = n - point_index - 1; pp = Arc.PointsAtEqualSegmentLength(arc, arc_points_count) for po in pp: on_arc_points.append(po) edge_arcs.append(arc) edges_arcs.append(edge_arcs) 

उफ़, और चाप नहीं काटना! बहुत अधिक धाराप्रवाह गुगली ने मुझे एक पुस्तक में नहीं लाया जो मेरी मान्यताओं की पुष्टि करता है कि भू-आकृतिक किनारे के शीर्ष के रूप में आर्क्स के प्रतिच्छेदन द्वारा गठित त्रिकोण के केंद्र का उपयोग करना आवश्यक है। मैंने एसिडिक के स्रोतों को भी धूम्रपान किया, लेकिन मुझे याद है कि क्या मुझे वहाँ पुष्टि नहीं मिली। मुझे याद है कि यह दिलचस्प था।
केंद्रों को किसी तरह मिल जाना चाहिए। यह त्रिकोण का केंद्र है और यह मुश्किल नहीं है, लेकिन यह समझना आवश्यक था कि ये त्रिकोण बिंदुओं के ढेर में कहां हैं। यह मुझे सबसे आसान विकल्प लग रहा था कि एक दूसरे के निकटतम बिंदुओं को जोड़ सकें।

 for point in on_arc_points: distance = [] #       . for p2 in on_arc_points: distance.append(point.DistanceTo(p2)) distance.sort() #    three_points = [] for p2 in on_arc_points: if point.DistanceTo(p2) <= distance[2]: three_points.append(p2); #   poly = Polygon.ByPoints(three_points) #   .     ,    result_points.append(poly.Center()) 

अब हमें विभिन्न चरणों में एकत्र किए गए बिंदुओं को आपस में जोड़ने की जरूरत है, जो कि जियोडेसिक क्षेत्र के किनारों के कोने हैं। तस्वीर में, ये बिंदु स्पष्ट रूप से दिखाई देते हैं, लेकिन जब वे सरणी में होते हैं - सब कुछ अधिक जटिल होता है। कई विकल्प थे, लेकिन चूंकि कार्य को कम से कम प्रयास के साथ एक काम करने वाली स्क्रिप्ट प्राप्त करना था, इसलिए यह सामने आया:

 #  -           ,    points = dict() for i, point in enumerate(projected): points[i] = dict() points[i]['point'] = point points[i]['id'] = i points[i]['distance'] = dict() for c, p2 in enumerate(projected): points[i]['distance'][c] = point.DistanceTo(p2) max_dist = 0 i = 0 for i, point in points.items(): max_distance = max(point['distance'].values()) if max_distance > max_dist: root_point = i max_dist = max_distance row = dict() row[root_point] = points[root_point] del points[root_point] surfaces = [] while len(row): #for x in range(0, 2): next_row = dict() for id, item in row.items(): point = closest_point(points, id) if point is not None: tmp = points[point] del points[point] point2 = closest_point(points, id) points[point] = tmp if point2 is not None: surfaces.append(Surface.ByPerimeterPoints([item['point'], points[point]['point'], points[point2]['point']])) next_row[point] = points[point] next_row[point2] = points[point2] for id, item in next_row.items(): point = closest_point(row, id) if point is not None: tmp = row[point] del row[point] point2 = closest_point(row, id) row[point] = tmp if point2 is not None: surfaces.append(Surface.ByPerimeterPoints([row[point]['point'], row[point2]['point'], item['point']])) row.clear() for id, po in next_row.items(): if po['id'] in points: del points[po['id']] if po['id'] not in row: row[po['id']] = po face_triangles = surfaces 

खण्ड तैयार है। शायद इस समस्या को हल करने के लिए किसी तरह का सही तरीका है, लेकिन मैंने अपना खुद का मार्ग प्रशस्त किया।



तब खंड सामने आता है, इसे कई बार कॉपी किया जाता है, कॉपी किया जाता है, और एक पूरा गोला प्राप्त होता है। यहाँ एक ट्विस्ट है:

 v = Vector.ByTwoPoints(sphere_center, curves[0].StartPoint) for face_triangle in face_triangles: geodesic_sphere.append(Geometry.Rotate(face_triangle, sphere_center, v, 72)) 

स्क्रिप्ट बदसूरत निकली, मैंने इसे एक-दो बार कॉपी किया, क्योंकि रेविट को एक्सपोर्ट करने में दिक्कतें आ रही थीं। सोचा कि निर्माण के साथ समस्याएं थीं। नतीजतन, डायनमो मंच पर, भारतीय ने यूक्रेनी को प्रेरित किया और सब कुछ सफल रहा!

अब आप किसी भी आवृत्ति और किसी भी व्यास का एक क्षेत्र बना सकते हैं। अम्लीय परिणामों के साथ आकारों की तुलना से पता चला कि सब कुछ उच्च सटीकता के साथ परिवर्तित होता है। पुनरावृत्ति अच्छी है।



मैंने फसल को कम करने के लिए आकारों का अनुकूलन शुरू कर दिया। चूंकि सभी आकार मेरे हाथों में थे, इसलिए यह इतना मुश्किल नहीं था। नतीजतन, गोले की त्रिज्या 5. की आवृत्ति पर 5.65 मीटर हो गई। इस तरह के आयामों ने मुझे 125 सेमी की चौड़ाई के साथ सामग्री का उपयोग करने की अनुमति काफी प्रभावी रूप से दी है। इस तरह की चौड़ाई OSB, शीट धातु, इन्सुलेशन, drywall की चादरें हैं। अच्छे अनुकूलन के साथ, कतरनों की संख्या न्यूनतम है। सामग्री पर त्रिकोण के लेआउट की गणना करके सर्वोत्तम परिणाम प्राप्त किए जा सकते हैं, लेकिन मैंने ऐसा नहीं किया।

इसके अलावा, यह आसान था, क्योंकि Revit ने एक जटिल आकार खा लिया और इसके साथ काम करने की अनुमति दी और उसी सफलता के साथ वर्ग-समानांतर के साथ।

बेशक, कठिनाइयों का अंत नहीं हुआ, लेकिन यह एक पूरी तरह से अलग कहानी है।