👩🏾‍🎓 😷 🥧 दीप सुदृढीकरण सीखना: मकड़ियों को कैसे चलना सिखाएं 👩‍❤️‍💋‍👨 👰🏾 👈🏿

आज मैं आपको बताऊंगा कि कैसे मैंने रोबोट को नियंत्रित करने के लिए सुदृढीकरण के गहन शिक्षण एल्गोरिदम को लागू किया। संक्षेप में, मैं आपको बताता हूँ कि "तंत्रिका नेटवर्क के साथ ब्लैक बॉक्स" कैसे बनाया जाए, जो इनपुट पर रोबोट वास्तुकला को स्वीकार करता है और एक एल्गोरिथ्म का उत्पादन करता है जो इसे आउटपुट पर नियंत्रित कर सकता है।

समाधान का मूल है एडवांटेज एक्टर क्रिटिक (ए 2 सी) एल्गोरिथ्म, एडवांटेज एडवांटेज एडवांटेज एस्टीमेशन (जीएई) के माध्यम से स्कोर।

कट के तहत, गणित, एक TensorFlow कार्यान्वयन, और चलने वाले एल्गोरिदम के किस प्रकार के बहुत सारे डेमो नीचे आए।

सामग्री:

- चुनौती
- सुदृढीकरण सीखना क्यों?
- सुदृढीकरण सीखने का विवरण
- नीति ढाल
- विकर्ण गौसियन नीतियाँ
- आलोचना को जोड़कर विचरण को कम करें
- नुकसान

- निष्कर्ष

कार्य

इस लेख में, हम रोबोट को म्यूजोको सिमुलेशन में चलना सिखाएंगे। हम रोबोट मॉडल के निर्माण और पर्यावरण के लिए पायथन इंटरफेस के साथ कदम का वर्णन छोड़ देंगे, क्योंकि वहाँ कुछ भी दिलचस्प नहीं है। समझने के लिए, केवल म्यूजिको में डेमो और जिम ओपनएआई में म्यूजिको के वातावरण के स्रोतों को देखें ।

इनपुट पर, एजेंट के पास म्यूजोको से कई नंबर होंगे: रिश्तेदार स्थिति, रोटेशन के कोण, गति, रोबोट के शरीर के कुछ हिस्सों का त्वरण, आदि। कुल में, ~ 800 सुविधाओं का क्रम। हम डीप लर्निंग दृष्टिकोण का उपयोग करते हैं और समझ नहीं पाएंगे कि वास्तव में उनका क्या मतलब है। मुख्य बात यह है कि इस संख्या के सेट में पर्याप्त जानकारी होगी ताकि एजेंट समझ सके कि उसके साथ क्या हो रहा है।

आउटपुट पर हम 18 नंबरों की उम्मीद करेंगे - रोबोट की स्वतंत्रता की डिग्री की संख्या, जिसका अर्थ है टिका का रोटेशन कोण जिस पर अंग तय हो गए हैं।

अंत में, एजेंट का लक्ष्य एपिसोड के लिए कुल इनाम को अधिकतम करना है। यदि रोबोट क्रैश हो जाता है या 3000 कदम (15 सेकंड) बीत चुके हैं तो हम एपिसोड को समाप्त कर देंगे। प्रत्येक चरण निम्न सूत्र के अनुसार एजेंट को पुरस्कृत करेगा:

$\ newcommand {\ E} {\ mathop {\ mathbb {E}}} \ newcommand {\ R} {\ mathop {\ mathbb {R}}} r_t = \ Delta x * 1000 + 0.5$

यानी एजेंट का लक्ष्य उसके समन्वय को बढ़ाएगा $x$ और प्रकरण के अंत तक गिर नहीं है।

तो, कार्य सेट है: फ़ंक्शन को खोजने के लिए $\ pi: \ R ^ {800} \ to \ R ^ {18}$ जिसके लिए एपिसोड के लिए इनाम सबसे बड़ा होगा । यह बहुत सही नहीं है? :) आइए देखते हैं कि दीप सुदृढीकरण सीखना इस कार्य को कैसे संभालता है ।

सुदृढीकरण सीखना क्यों?

चलने वाले रोबोटों की गति की समस्या को हल करने के लिए आधुनिक दृष्टिकोण शास्त्रीय रोबोटिक्स प्रथाओं से मिलकर बनता है जो इष्टतम नियंत्रण और प्रक्षेपवक्र अनुकूलन : LQR, QP, उत्तल अनुकूलन है। और पढ़ें: एटलस पर बोस्टन डायनेमिक्स टीम पोस्ट

ये तकनीक एक तरह की "हार्डकोडिंग" है क्योंकि उन्हें नियंत्रण एल्गोरिदम में सीधे कार्य के कई विवरणों की शुरूआत की आवश्यकता होती है। उनमें कोई सीखने की प्रणाली नहीं है - अनुकूलन "मौके पर" होता है।

दूसरी ओर, सुदृढीकरण सीखना (इसके बाद आरएल) को एल्गोरिथ्म में परिकल्पनाओं की आवश्यकता नहीं होती है, जिससे समस्या का समाधान अधिक सामान्य और मापनीय हो जाता है।

सुदृढीकरण सीखने का विवरण

स्रोत

आरएल समस्या में, हम एजेंट और पर्यावरण की बातचीत को जोड़े के एक अनुक्रम (राज्य, इनाम) और उनके बीच के बदलावों के रूप में मानते हैं - कार्रवाई ।

$(s_0) \ xrightarrow {a_0} (s_1, r_1) \ xrightarrow {a_ {1}} ... \ xrightarrow {a_ {n-1}} (s_n, rn)$

शब्दावली को परिभाषित करें:

$\ pi (a_t। s_t)$ - नीति , एजेंट व्यवहार रणनीति, सशर्त संभाव्यता,
$a_t \ sim \ pi (\ cdot | s_t)$ - वितरण से कार्रवाई को एक यादृच्छिक चर माना जाता है $\ pi$ ।
हम नीति को एक कार्य के रूप में मान सकते हैं $\ pi: स्टेट्स टू एक्ट्स$ , लेकिन हम एजेंट कार्यों को स्टोचस्टिक बनाना चाहते हैं, जो अन्वेषण की सुविधा प्रदान करता है । यानी कुछ संभावना के साथ हम उन कार्यों को नहीं करते हैं जो एजेंट चुनता है।
$\ _ ताऊ$ - एजेंट, अनुक्रम द्वारा प्रक्षेपवक्र का पता लगाया $(s_1, s_2, ..., s_n)$ ।

एजेंट का कार्य अपेक्षित रिटर्न को अधिकतम करना है :

$J (\ pi) = \ E _ {\ _ tau \ sim \ pi} [R (\ tau)] = \ E _ {\ _ tau \ sim \ pi} \ बाएँ [\ sum_ {t = 0} ^ n_t \ right ]$

अब हम RL समस्या को हल कर सकते हैं, खोजें:

$\ pi ^ * = arg \ mathop {max} _ \ pi J (\ pi)$

जहाँ $\ pi ^ *$ इष्टतम नीति है।

OpenAI से सामग्री में और पढ़ें: OpenAI Spinning Up

नीति ढाल

यह उल्लेखनीय है कि अनुकूलन समस्या के रूप में आरएल समस्या का एक कठोर बयान हमें उदाहरण के लिए पहले से ही ज्ञात अनुकूलन विधियों का उपयोग करने का अवसर देता है। जरा कल्पना करें कि यदि हम मॉडल मापदंडों द्वारा अपेक्षित रिटर्न ग्रेडिएंट ले सकते हैं तो यह कितना अच्छा होगा: $\ nabla_ \ theta J (\ pi_ \ theta)$ । इस मामले में, तराजू को अद्यतन करने का नियम सरल होगा:

$\ theta = \ theta_ {पुराना} + \ Alpha \ nabla_ \ theta J (\ pi_ \ theta)$

यह सभी नीतिगत ढाल विधियों का ठीक-ठीक विचार है। इस ढाल का सख्त निष्कर्ष कुछ हद तक कट्टर है। हम इसे यहां नहीं लिखेंगे, लेकिन OpenAI से अद्भुत सामग्री के लिए एक लिंक छोड़ देंगे । ढाल इस तरह दिखता है:

$\ nabla_ \ theta J (\ pi_ \ theta) = \ E _ {\ _ tau \ sim \ pi_ \ theta} \ left [\ sum_ {t = 0} ^ T \ nabla_ \ theta \ log \ pi_ \ theta (a_t_) | s_t) R (\ tau) \ right]$

इस प्रकार, हमारे मॉडल का नुकसान इस तरह होगा:

$हानि = - \ log (\ pi_ \ theta (a_t | s_t)) R (\ tou)$

उसको याद करो $R (\ tau) = \ sum_ {t = 0} ^ T r_t$ , और $\ pi_ \ theta (a_t | s_t)$ - यह उस समय हमारे मॉडल का आउटपुट है जब वह अंदर थी $s_t$ । इस तथ्य के कारण माइनस दिखाई दिया कि हम अधिकतम करना चाहते हैं $जे$ । प्रशिक्षण के दौरान, हम बैचों पर ग्रेडिएंट पर विचार करेंगे और उन्हें विचरण को कम करने के लिए जोड़ेंगे (स्टोकेस्टिक वातावरण के कारण डेटा शोर)।

यह एक कार्यशील एल्गोरिदम है जिसे REINFORCE कहा जाता है। और वह जानता है कि कुछ सरल वातावरण के लिए समाधान कैसे खोजना है। उदाहरण के लिए, "कार्टपोल-वी 2" ।

एजेंट कोड पर विचार करें:

class ActorNetworkDiscrete: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=20, activation=tf.nn.relu) output_linear = tf.layers.dense(l1, units=action_space) output = tf.nn.softmax(output_linear) self.action_op = tf.squeeze(tf.multinomial(logits=output_linear,num_samples=1), axis=1) # Training output_log = tf.nn.log_softmax(output_linear) self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None], dtype=tf.int32) action_one_hot = tf.one_hot(self.action_ph, action_space) responsible_output_log = tf.reduce_sum(output_log * action_one_hot, axis=1) self.loss = -tf.reduce_mean(responsible_output_log * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) actor = ActorNetworkDiscrete()

हमारे पास इस वास्तुकला का एक छोटा बोधक है: (अवलोकन_क्षेत्र, 10, क्रिया_क्षेत्र) [कार्टपोल के लिए यह है (4, 10, 2)]। tf.multinomial आप बेतरतीब ढंग से भारित एक कार्रवाई का चयन करने की अनुमति देता है। एक कार्रवाई करने के लिए आपको कॉल करने की आवश्यकता है:

 action = sess.run(actor.action_op, feed_dict={actor.state_ph: observation})

और इसलिए हम उसे प्रशिक्षित करेंगे:

 batch_generator = generate_batch(environments, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, total reward] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]})

बैच जनरेटर पर्यावरण में एजेंट चलाता है और प्रशिक्षण के लिए डेटा जमा करता है। बैच के तत्व इस तरह के होते हैं: $(s_t, a_t, R (\ tau))$ ।

एक अच्छा जनरेटर लिखना एक अलग कार्य है, जहां मुख्य कठिनाई एकल सिमुलेशन चरण (यहां तक कि म्यूजो) की तुलना में sess.run () कॉल करने की सापेक्ष उच्च लागत है। काम को गति देने के लिए, आप इस तथ्य का फायदा उठा सकते हैं कि तंत्रिका नेटवर्क बैचों पर चलते हैं, और कई समानांतर वातावरण का उपयोग करते हैं। यहां तक कि क्रमिक रूप से उन्हें एक धागे में लॉन्च करने से एकल वातावरण की तुलना में महत्वपूर्ण त्वरण होगा।

OpenAI बेसलाइन से DummyVecEnv का उपयोग कर जेनरेटर कोड

 # Vectorized environments with gym-like interface from baselines.common.vec_env.subproc_vec_env import SubprocVecEnv from baselines.common.vec_env.dummy_vec_env import DummyVecEnv def make_env(env_id, seed): def _f(): env = gym.make(env_name) env.reset() # Desync environments for i in range(int(200 * seed // environments_count)): env.step(env.action_space.sample()) return env return _f envs = [make_env(env_name, seed) for seed in range(environments_count)] # Can be switched to SubprocVecEnv to parallelize on cores # (for computationally heavy envs) envs = DummyVecEnv(envs) # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py def discount_cumsum(x, coef): """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def generate_batch(envs, batch_size, replay_buffer_size): envs_number = envs.num_envs observations = [[0 for i in range(observation_space)] for i in range(envs_number)] # [state, action, discounted reward-to-go] replay_buffer = np.empty((0,3), np.float32) # [state, action, reward] rollout lists for every environment instance rollouts = [np.empty((0, 3)) for i in range(envs_number)] while True: history = {'reward': [], 'max_action': []} replay_buffer = replay_buffer[batch_size:] # Main sampling cycle while len(replay_buffer) < replay_buffer_size: # Here policy acts in environments. Note that it chooses actions for all # environments in one batch, therefore expensive sess.run is called once. actions = sess.run(actor.action_op, feed_dict={actor.state_ph: observations}) observations_old = observations observations, rewards, dones, _ = envs.step(actions) history['max_action'].append(np.abs(actions).max()) time_point = np.array(list(zip(observations_old, actions, rewards))) for i in range(envs_number): # Regular python-like append rollouts[i] = np.append(rollouts[i], [time_point[i]], axis=0) # Process done==True environments if dones.all(): print('WARNING: envs are in sync!! This makes sampling inefficient!') done_indexes = np.arange(envs_number)[dones] for i in done_indexes: rewards_trajectory = rollouts[i][:, 2].copy() history['reward'].append(rewards_trajectory.sum()) rollouts[i][:, 2] = discount_cumsum(rewards_trajectory, coef=discount_factor) replay_buffer = np.append(replay_buffer, rollouts[i], axis=0) rollouts[i] = np.empty((0, 3)) # Shuffle before yield to become closer to iid np.random.shuffle(replay_buffer) # Truncate replay_buffer to get the most relevant feedback from environment replay_buffer = replay_buffer[:replay_buffer_size] yield replay_buffer[:batch_size], history # Make a test yield a = generate_batch(envs, 8, 64) # Makes them of equal lenght for i in range(10): next(a) next(a)[0]

परिणामी एजेंट वातावरण में क्रियाओं के सीमित स्थान के साथ खेल सकता है। यह प्रारूप हमारे कार्य के लिए उपयुक्त नहीं है। रोबोट को नियंत्रित करने वाले एजेंट को एक वेक्टर जारी करना चाहिए $\ R ^ n$ जहाँ $एन$ - स्वतंत्रता की डिग्री की संख्या। ( या आप एक्शन स्पेस को अंतराल में विभाजित कर सकते हैं और असतत आउटपुट के साथ एक कार्य प्राप्त कर सकते हैं )

विकर्ण गौसियन नीतियाँ

डायगोनल गॉसियन नीतियों के दृष्टिकोण का सार मॉडल के लिए n-आयामी सामान्य वितरण के मापदंडों का उत्पादन करने के लिए है, अर्थात् $\ _मु_ \ थीटा$ - चटाई। प्रतीक्षा और $\ _ सिग्मा_ \ थीटा$ - मानक विचलन। जैसे ही एजेंट को कार्रवाई करने की आवश्यकता होती है, हम इन मापदंडों को मॉडल से पूछेंगे और इस वितरण से एक यादृच्छिक चर लेंगे। इसलिए हमने एजेंट को बाहर कर दिया $\ R ^ n$ और इसे स्टोकेस्टिक बना दिया। सबसे महत्वपूर्ण बात यह है कि आउटपुट पर वितरण वर्ग को तय करने के बाद, हम गणना कर सकते हैं $\ log (\ pi_ \ theta (a_t | s_t))$ और इसलिए नीति ढाल।

नोट: तय किया जा सकता है $\ _ सिग्मा_ \ थीटा$ हाइपरपरमीटर के रूप में, जिससे आउटपुट आयाम कम हो जाता है। अभ्यास से पता चलता है कि इससे बहुत नुकसान नहीं होता है, लेकिन, इसके विपरीत, सीखने को स्थिर करता है।

स्टोकेस्टिक नीति पर अधिक पढ़ें ।

एजेंट कोड:

 epsilon = 1e-8 def gaussian_loglikelihood(x, mu, log_std): pre_sum = -0.5 * (((x - mu) / (tf.exp(log_std) + epsilon))**2 + 2 * log_std + np.log(2 * np.pi)) return tf.reduce_sum(pre_sum, axis=1) class ActorNetworkContinuous: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) mu = tf.layers.dense(l3, units=action_space) log_std = tf.get_variable(name='log_std', initializer=-0.5 * np.ones(action_space, std = tf.exp(log_std) self.action_op = mu + tf.random.normal(shape=tf.shape(mu)) * std # Training self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None, action_space], dtype=tf.float32) action_logprob = gaussian_loglikelihood(self.action_ph, mu, log_std) self.loss = -tf.reduce_mean(action_logprob * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss)

प्रशिक्षण भाग अलग नहीं है।

अब हम अंत में देख सकते हैं कि कैसे REINFORCE हमारे कार्य के साथ सामना करेगा। इसके बाद, एजेंट का लक्ष्य दाईं ओर बढ़ना है।

धीरे-धीरे लेकिन निश्चित रूप से अपने लक्ष्य की ओर बढ़ रहा है।

पुरस्कृत करने के लिए जाने

ध्यान दें कि हमारे ग्रेडिएंट में अतिरिक्त सदस्य हैं। हर कदम पर नमस्कार $टी$ जब लघुगणक के वजन को कम करते हुए, हम पूरे प्रक्षेपवक्र के लिए कुल इनाम का उपयोग करते हैं। इस प्रकार, अतीत से अपनी उपलब्धियों के द्वारा एजेंट के कार्यों का मूल्यांकन करना। गलत लगता है, है ना? इसलिए यह

$\ nabla_ \ theta J (\ pi_ \ theta) = \ E _ {\ _ tau \ sim \ pi_ \ theta} \ left [\ sum_ {t = 0} ^ T \ nabla_ \ theta \ log \ pi_ \ theta (a_t_) | s_t) \ sum_ {t '= 0} ^ T r_ {t'} \ right]$

यह बन जाएगा

$\ nabla_ \ theta J (\ pi_ \ theta) = \ E _ {\ _ tau \ sim \ pi_ \ theta} \ left [\ sum_ {t = 0} ^ T \ nabla_ \ theta \ log \ pi_ \ theta (a_t_) | s_t) \ sum_ {t '= t} ^ T r_ {t'} \ right]$

10 अंतर खोजें :)

जबकि इन सदस्यों की उपस्थिति गणितीय रूप से कुछ भी नहीं बिगाड़ती है, यह हमारे लिए बहुत शोर करता है। अब, प्रशिक्षण के दौरान, एजेंट केवल उन पुरस्कारों पर ध्यान देगा जो उन्हें एक विशिष्ट कार्रवाई के बाद मिले थे।

इस सुधार के कारण, औसत इनाम बढ़ा है। प्राप्त एजेंटों में से एक ने अपने लक्ष्य को प्राप्त करने के लिए forelimbs का उपयोग करना सीखा:

आलोचना को जोड़कर विचरण को कम करें

आगे के सुधारों का सार माध्यम के राज्यों के बीच स्टोकेस्टिक संक्रमण के कारण उत्पन्न होने वाले शोर (विचरण) में कमी है।

यह हमें एक मॉडल जोड़ने में मदद करेगा, जो राज्य से शुरू होने वाले एजेंट द्वारा प्राप्त पुरस्कारों की औसत राशि की भविष्यवाणी करेगा $एस$ प्रक्षेपवक्र के अंत तक, अर्थात्। मान समारोह।

$V ^ \ pi (s) = \ E _ {\ tau \ sim \ pi} \ left [R (\ tau) | s_0 = s \ right] \ text {- मान फ़ंक्शन}$

$Q ^ \ pi (s) = \ E _ {\ tau \ sim \ pi} \ left [R (\ tau) | s_0 = s, a_0 = a \ right] \ text {- Action-Value =}$

$A ^ \ pi (s), Q ^ \ pi (s, a) -V ^ \ pi (s) \ text {- लाभ फ़ंक्शन}$

मान फ़ंक्शन अपेक्षित वापसी दिखाता है यदि हमारी नीति एक विशिष्ट राज्य से खेल शुरू करती है। क्यू-फ़ंक्शन के साथ भी ऐसा ही है, बस बहुत पहले कार्रवाई को ठीक करें।

आलोचना जोड़ें

इनाम-दर-गो का उपयोग करते समय यह ढाल कैसी दिखती है:

$\ nabla_ \ theta \ log \ pi_ \ theta (a_t | s_t) \ sum_ {t '= t} ^ T r_ {t'}$

अब लघुगणक के ढाल के लिए गुणांक मान फ़ंक्शन के नमूने से अधिक कुछ नहीं है।

$\ sum_ {t '= t} ^ T r_ {t'} \ sim V ^ \ pi (s_t)$

हम एक विशेष प्रक्षेपवक्र से एक नमूने के साथ लघुगणक ढाल का वजन करते हैं, जो अच्छा नहीं है। हम कुछ मॉडल के साथ मान-फ़ंक्शन को अनुमानित कर सकते हैं, उदाहरण के लिए, एक तंत्रिका नेटवर्क, और इससे आवश्यक मूल्य पूछते हैं, जिससे विचरण को कम किया जा सकता है। हम इस मॉडल को आलोचक (क्रिटिक) कहेंगे और हम इसे नीति के समानांतर अध्ययन करेंगे। इस प्रकार, ढाल सूत्र के रूप में लिखा जा सकता है:

$\ nabla_ \ theta \ log \ pi_ \ theta (a_t। s_t) \ sum_ {t '= t} ^ T r_ {t'} \ लगभग \ nabla_ \ theta's log \ pi_ \ theta (a_t। s_t) V ^ | \ pi (\ tau)$

हमने विचरण को कम किया, लेकिन साथ ही, हमने अपने एल्गोरिथ्म में पूर्वाग्रह पेश किया, क्योंकि तंत्रिका नेटवर्क सन्निकटन त्रुटियां कर सकते हैं। लेकिन इस स्थिति में समझौता अच्छा है। मशीन लर्निंग में ऐसी स्थितियों को पूर्वाग्रह-परिवर्तन व्यापार कहा जाता है।

आलोचक पर्यावरण में एकत्र किए गए इनाम-टू-गो नमूनों पर मूल्य-फ़ंक्शन प्रतिगमन सिखाएगा। एक त्रुटि समारोह के रूप में, हम एमएसई लेते हैं। यानी नुकसान इस तरह दिखता है:

$हानि = ({V} ^ \ pi_ \ psi (s_t) - \ sum_ {t '= t} ^ T r_ {t'}) ^ $$

आलोचना कोड:

 class CriticNetwork: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) output = tf.layers.dense(l3, units=1) self.value_op = tf.squeeze(output, axis=-1) # Training self.value_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.loss = tf.losses.mean_squared_error(self.value_ph, self.value_op) optimizer = tf.train.AdamOptimizer(learning_rate=critic_learning_rate) self.update_op = optimizer.minimize(self.loss)

प्रशिक्षण चक्र अब इस तरह दिखता है:

 batch_generator = generate_batch(envs, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, value, reward-to-go] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) # Train critic for j in range(10): _, critic_loss = sess.run([critic.update_op, critic.loss], feed_dict={critic.state_ph: batch[:, 0], critic.value_ph: batch[:, 3]})

अब बैच में एक और मूल्य, मूल्य, जनरेटर में आलोचक द्वारा गणना की जाती है।
यानी बैच का प्रकार यह है: $(s_t, a_t, V ^ \ pi_ \ psi (s_t), \ sum_ {t '= t} ^ T r_ {t'})$ ।

चक्र में, आलोचक को अभिसरण के प्रशिक्षण से कुछ भी सीमित नहीं करता है, इसलिए हम ग्रेडिएंट वंश के कई कदम उठाते हैं, जिससे मूल्य फ़ंक्शन के अनुमान में सुधार होता है और पूर्वाग्रह कम होते हैं। हालांकि, इस दृष्टिकोण को पुनः प्रयास से बचने के लिए एक बड़े बैच आकार की आवश्यकता होती है। सीखने की नीति के बारे में एक समान कथन सत्य नहीं है। इसे सीखने के माहौल से तुरंत प्रतिक्रिया मिलनी चाहिए, अन्यथा हम खुद को ऐसी स्थिति में पा सकते हैं जहां हम उन कार्यों के लिए नीति को ठीक करते हैं जो पहले से ही नहीं किए गए थे। इस संपत्ति वाले एल्गोरिदम को ऑन-पॉलिसी कहा जाता है।

पॉलिसी ग्रेजुएट्स में बेसलाइन

यह दिखाया जा सकता है कि ग्रेडिएंट में अन्य उपयोगी कार्यों की एक विस्तृत कक्षा लगाने की अनुमति है $टी$ । ऐसे कार्यों को आधार रेखा कहा जाता है। ( इस तथ्य का निष्कर्ष ) निम्नलिखित कार्य आधारभूत कार्य करते हैं:

स्रोत: जीएई पेपर

विभिन्न आधारभूत कार्य के आधार पर अलग-अलग परिणाम देते हैं। एक नियम के रूप में, सबसे बड़ा लाभ एडवांटेज फ़ंक्शन और इसके अनुमानों द्वारा दिया जाता है।

इसके पीछे थोड़ा अंतर्ज्ञान भी है। जब हम एडवांटेज का उपयोग करते हैं, तो हम उस अनुपात में एजेंट को ठीक करते हैं, जो एजेंट द्वारा की गई कार्रवाई से औसत से ज्यादा बेहतर या खराब होता है। और एजेंट जितना बेहतर पर्यावरण में खेलता है, उसके मानक उतने ही ऊंचे होते जाते हैं । आदर्श एजेंट अच्छा खेलेगा और अपने सभी कार्यों का मूल्यांकन करेगा, क्योंकि एडवांटेज 0 के बराबर है और इसलिए, 0 के बराबर ग्रेडिएंट है।

वैल्यू फ़ंक्शन के माध्यम से लाभ मूल्यांकन

एडवांटेज की परिभाषा याद करें:

$A ^ \ pi (s), Q ^ \ pi (s, a) -V ^ \ pi (s) \ text {- लाभ फ़ंक्शन}$

यह स्पष्ट नहीं है कि इस तरह के फ़ंक्शन को स्पष्ट रूप से कैसे सीखा जाए। बचाव के लिए एक ट्रिक आएगी, जो एडवांटेज फ़ंक्शन की गणना को वैल्यू फ़ंक्शन की गणना में कम कर देगी।

परिभाषित $\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - अस्थायी अंतर अवशिष्ट ( टीडी-अवशिष्ट )। यह कहना मुश्किल नहीं है कि इस तरह के एक समारोह का फायदा होता है:

$\ E \ left [\ delta ^ V_t \ right] = \ E \ left [r_t + V (s_ {t + 1}) - V (s_t) \ right] = \ E \ left [Q (s_t, a_t) -V (s_t) \ right] = A (s_t, a_t)$

इस तरह का एक वैचारिक रूप से जटिल बदलाव कोड में इतना बड़ा बदलाव नहीं होने के लिए उकसाता है। अब, मान फ़ंक्शन का मूल्यांकन करने के बजाय, आलोचक नीति प्रशिक्षण के लिए एक लाभ मूल्यांकन प्रस्तुत करेगा।

परिणामी एल्गोरिदम को एडवांटेज एक्टर-क्रिटिक कहा जाता है।

 def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + np.append(values[1:], np.array([0])) return deltas, values

प्राप्त एजेंटों को आत्मविश्वास से प्रभावित और अंगों के समकालिक उपयोग के लिए देखा जा सकता है:

सामान्यीकृत लाभ अनुमान

एक अपेक्षाकृत हालिया लेख (2018), " सामान्यीकृत लाभ आकलन का उपयोग करके उच्च-आयामी निरंतर नियंत्रण ", मूल्य फ़ंक्शन के माध्यम से एडवांटेज का और भी अधिक कुशल मूल्यांकन प्रदान करता है। यह अधिक विचरण को कम करता है:

$A_t ^ {GAE (\ gamma, \ lambda)} = \ sum_ {l = 0} ^ \ infty (\ gamma \ lambda) ^ l \ डेल्टा ^ V_ {t + l}$

जहां:

$\ delta_t ^ V = r_t + V (s_ {t + 1}) - V (s_t)$ - टीडी-अवशिष्ट,
$गामा$ - डिस्काउंट फैक्टर (हाइपरपरमीटर),
$\ lambda$ - हाइपरपरमीटर।

व्याख्या को प्रकाशन में ही पाया जा सकता है।

कार्यान्वयन:

 def discount_cumsum(x, coef): # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + discount_factor * np.append(values[1:], np.array([0])) advantage = discount_cumsum(deltas, coef=lambda_factor * discount_factor) return advantage, values

एक छोटे बैच आकार का उपयोग करते समय, एल्गोरिथ्म कुछ स्थानीय ऑप्टिमा में परिवर्तित हो जाता है। यहाँ, एजेंट एक पंजा के रूप में एक पंजा का उपयोग करता है, और बाकी को धक्का देता है:

यहां, एजेंट जंप के उपयोग के लिए नहीं आया था, लेकिन बस अंगों के साथ जल्दी से ऊँगली कर रहा था। और आप यह भी देख सकते हैं कि वह कैसा बर्ताव करता है, अगर वह हिचकिचाता है, तो वह चारों ओर घूमेगा और दौड़ता रहेगा:

सबसे अच्छा एजेंट, वह लेख के बहुत शुरुआत में है। स्थिर कूद, जिसके दौरान सभी अंग सतह से बाहर आते हैं। संतुलन की विकसित क्षमता एजेंट को त्रुटि होने पर पूर्ण गति से प्रक्षेपवक्र को सही करने की अनुमति देती है:

नुकसान

मशीन लर्निंग त्रुटियों के स्थान के आयाम के लिए प्रसिद्ध है जिसे बनाया जा सकता है और पूरी तरह से गैर-काम करने वाला एल्गोरिदम प्राप्त कर सकता है। लेकिन आरएल समस्या को एक नए स्तर पर ले जाता है।

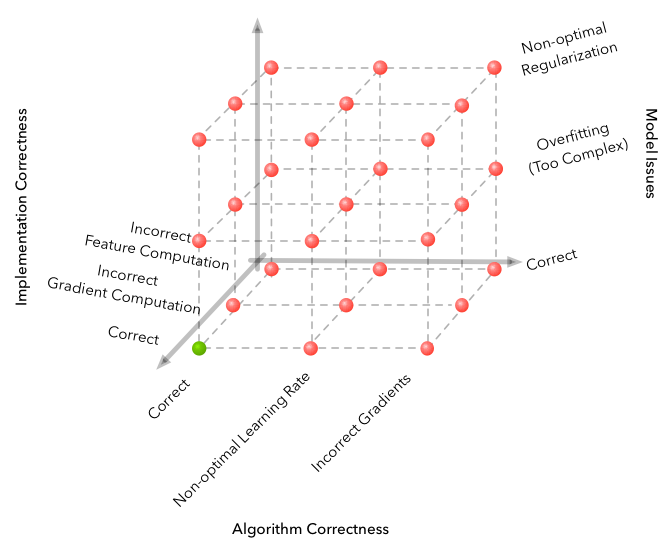
स्रोत

यहां विकास के दौरान आने वाली कठिनाइयों का सामना किया गया है।

एल्गोरिथ्म हाइपरपरमेटर्स के लिए आश्चर्यजनक रूप से संवेदनशील है। 3e-4 से 1e-4 में सीखने की दर को बदलते समय सीखने की गुणवत्ता में बदलाव आया। और तस्वीर मौलिक रूप से बदल गई - पूरी तरह से गैर-अभिसरण एल्गोरिथ्म से सबसे अच्छा जो वीडियो में है।
बैच का आकार डीएल के अन्य क्षेत्रों के समान नहीं है। यदि छवि वर्गीकरण में आप अपने आप को 32-256 बैच के आकार का चयन करने की अनुमति दे सकते हैं और परिणाम विशेष रूप से इसे बढ़ाने से नहीं बदलेगा, तो हमारे कार्य के लिए कुछ हजार, 3000 काम करना बेहतर होगा। और फिर से एक अच्छा एल्गोरिथ्म में अभिसरण की कमी से।
सीखना कई बार चलाना बेहतर होता है, कभी-कभी यादृच्छिक बीज भाग्यशाली नहीं होता है।
ऐसे जटिल वातावरण में सीखना बहुत समय लेता है, और प्रगति एक समान नहीं होती है। उदाहरण के लिए, 8 घंटे के लिए सबसे अच्छा एल्गोरिथ्म सीखा, जिनमें से 3 ने यादृच्छिक आधार रेखा की तुलना में खराब परिणाम दिखाया। इसलिए, एल्गोरिदम का परीक्षण करते समय, एक छोटे से शुरू करना बेहतर होता है, जैसे जिम से खिलौना वातावरण।
हाइपरपरमेटर्स और मॉडल आर्किटेक्चर खोजने का एक अच्छा तरीका संबंधित लेखों और कार्यान्वयन पर झांकना होगा। (मुख्य बात यह है कि पीछे हटना नहीं है)

आप इस लेख से डीप आरएल की बारीकियों के बारे में अधिक जान सकते हैं: डीप रिनफोर्स लर्निंग इज़ नॉट वर्क ।

निष्कर्ष

परिणामस्वरूप एल्गोरिथ्म समस्या को हल करता है। फंक्शन मिला $\ pi: \ R ^ {800} \ to \ R ^ {18}$ , संयत और आत्मविश्वास से रोबोट को नियंत्रित करता है।

एक तार्किक निरंतरता A2C, PPO और TRPO एल्गोरिदम के करीबी रिश्तेदारों का अध्ययन होगा। वे नमूना दक्षता में सुधार करते हैं, अर्थात्। एल्गोरिथ्म का अभिसरण समय, और वे अधिक जटिल समस्याओं को हल करने में सक्षम हैं। यह पीपीओ + ऑटोमैटिक डोमेन रेंडमाइजेशन था जिसने हाल ही में एक रोबोट पर रूबिक क्यूब को इकट्ठा किया ।

यहां आप लेख से कोड पा सकते हैं: रिपॉजिटरी ।

मुझे उम्मीद है कि आपको यह लेख अच्छा लगा होगा और इससे प्रेरित थे कि आज डीप रेनफोर्स लर्निंग क्या कर सकता है

आपका ध्यान के लिए धन्यवाद!

उपयोगी लिंक:

इस परियोजना में मदद करने के लिए पिंकोट्टर , वामबाला , एंड्री_प्रोबोच्किन , पॉलीफॉम और सुरिकनिक को धन्यवाद।
विशेष रूप से, वम्बाला और andrey_probochkin के लिए एक शांत MuJoCo वातावरण बनाने के लिए।

दीप सुदृढीकरण सीखना: मकड़ियों को कैसे चलना सिखाएं