 सूचना सिद्धांत से अवधारणाओं के दृश्य के लिए समर्पित एक दिलचस्प देशांतर का अनुवाद। पहले भाग में, हम इस बात पर ध्यान देंगे कि संभाव्यता वितरण, उनकी सहभागिता और सशर्त संभावनाओं का रेखांकन कैसे करें। अगला, हम फिक्स्ड और वेरिएबल लेंथ कोड से निपटेंगे, देखें कि इष्टतम कोड कैसे बनाया जाता है और ऐसा क्यों है। एक पूरक के रूप में, सिम्पसन सांख्यिकीय विरोधाभास नेत्रहीन समझा जाता है।
सूचना सिद्धांत से अवधारणाओं के दृश्य के लिए समर्पित एक दिलचस्प देशांतर का अनुवाद। पहले भाग में, हम इस बात पर ध्यान देंगे कि संभाव्यता वितरण, उनकी सहभागिता और सशर्त संभावनाओं का रेखांकन कैसे करें। अगला, हम फिक्स्ड और वेरिएबल लेंथ कोड से निपटेंगे, देखें कि इष्टतम कोड कैसे बनाया जाता है और ऐसा क्यों है। एक पूरक के रूप में, सिम्पसन सांख्यिकीय विरोधाभास नेत्रहीन समझा जाता है।सूचना सिद्धांत हमें कई चीजों का वर्णन करने के लिए एक सटीक भाषा देता है। मुझमें कितनी अनिश्चितता है? प्रश्न A के उत्तर का कितना ज्ञान मुझे प्रश्न B के उत्तर के बारे में बताता है? विश्वासों का एक सेट दूसरे के समान कैसे है? मेरे पास इन विचारों के अनौपचारिक संस्करण थे जब मैं एक छोटा बच्चा था, लेकिन सूचना का सिद्धांत उन्हें सटीक, शक्तिशाली विचारों में क्रिस्टलीकृत करता है। इन विचारों में डेटा संपीड़न से लेकर क्वांटम भौतिकी, मशीन लर्निंग और उनके बीच के विशाल क्षेत्रों में कई तरह के अनुप्रयोग हैं।
दुर्भाग्य से, सूचना सिद्धांत भयभीत कर सकता है। मुझे नहीं लगता कि इसका कोई कारण है। वास्तव में, कई प्रमुख विचारों को स्पष्ट रूप से समझाया जा सकता है!
संभाव्यता वितरण विज़ुअलाइज़ेशन
इससे पहले कि हम सूचना के सिद्धांत में तल्लीन हों, आइए इस बारे में सोचें कि आप सरल संभाव्यता वितरण की कल्पना कैसे कर सकते हैं। हमें बाद में उनकी आवश्यकता होगी, इसके अलावा, संभावनाओं की कल्पना करने की ये तकनीक अपने आप में उपयोगी हैं!
मैं कैलिफ़ोर्निया में हूं। कभी-कभी बारिश होती है, लेकिन ज्यादातर सूरज! कहो, उस समय का 75% धूप है। चित्र में दिखाना आसान है:
ज्यादातर दिन मैं एक टी-शर्ट पहनता हूं, लेकिन कभी-कभी मैं रेनकोट पहनता हूं। मान लीजिए कि मैं 38% समय एक रेनकोट पहनता हूं। यह चित्रित करना भी आसान है।
क्या होगा अगर मैं एक ही समय में दोनों तथ्यों की कल्पना करना चाहता हूं? यह आसान है अगर वे बातचीत नहीं करते हैं - अर्थात स्वतंत्र हैं। उदाहरण के लिए, यदि वह: मैं आज टी-शर्ट या रेनकोट पहनता हूं तो अगले सप्ताह मौसम पर निर्भर नहीं करता। हम इसे एक अक्ष के लिए एक चर के लिए और दूसरे के लिए एक का उपयोग करके चित्रित कर सकते हैं:

सीधी खड़ी और क्षैतिज रेखाओं पर ध्यान दें। आजादी कैसी दिखती है! एक रेनकोट पहनने की संभावना इस तथ्य के कारण नहीं बदलेगी कि एक सप्ताह में बारिश होगी। दूसरे शब्दों में, संभावना है कि मैं एक रेनकोट पहनूंगा और अगले सप्ताह बारिश होगी यह संभावना के बराबर है कि मैं एक रेनकोट पहनने की संभावना की संभावना है कि यह बारिश होगी। वे बातचीत नहीं करते हैं।
जब चर बातचीत करते हैं, तो कुछ जोड़े चर की संभावना बढ़ सकती है और दूसरों के लिए घट सकती है। एक उच्च संभावना है कि मैं एक रेनकोट पहनता हूं और बारिश होती है क्योंकि चर परस्पर संबंधित होते हैं, वे एक दूसरे को अधिक संभावना बनाते हैं। यह अधिक संभावना है कि मैं एक दिन रेनकोट पहनता हूं जब यह संभावना की तुलना में बारिश होती है कि मैं एक दिन रेनकोट पहनता हूं और एक और यादृच्छिक दिन पर बारिश होती है।
नेत्रहीन, ऐसा लगता है जैसे कुछ वर्गों में एक अतिरिक्त संभावना के साथ सूजन आती है, जबकि दूसरे वर्ग संकीर्ण होते हैं, क्योंकि कुछ घटनाओं की एक साथ होने की संभावना नहीं है:
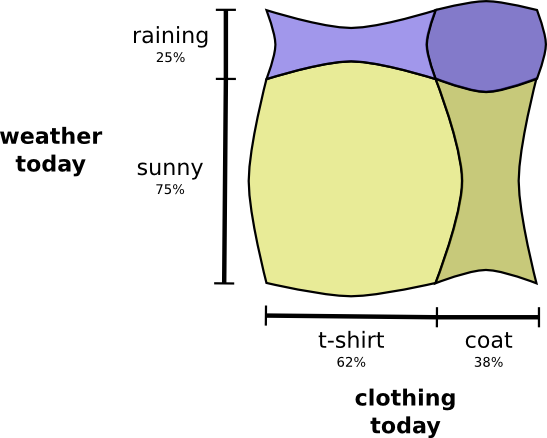
लेकिन हालांकि यह अच्छा लग रहा है, लेकिन यह समझने के लिए बहुत उपयोगी नहीं है कि क्या हो रहा है।
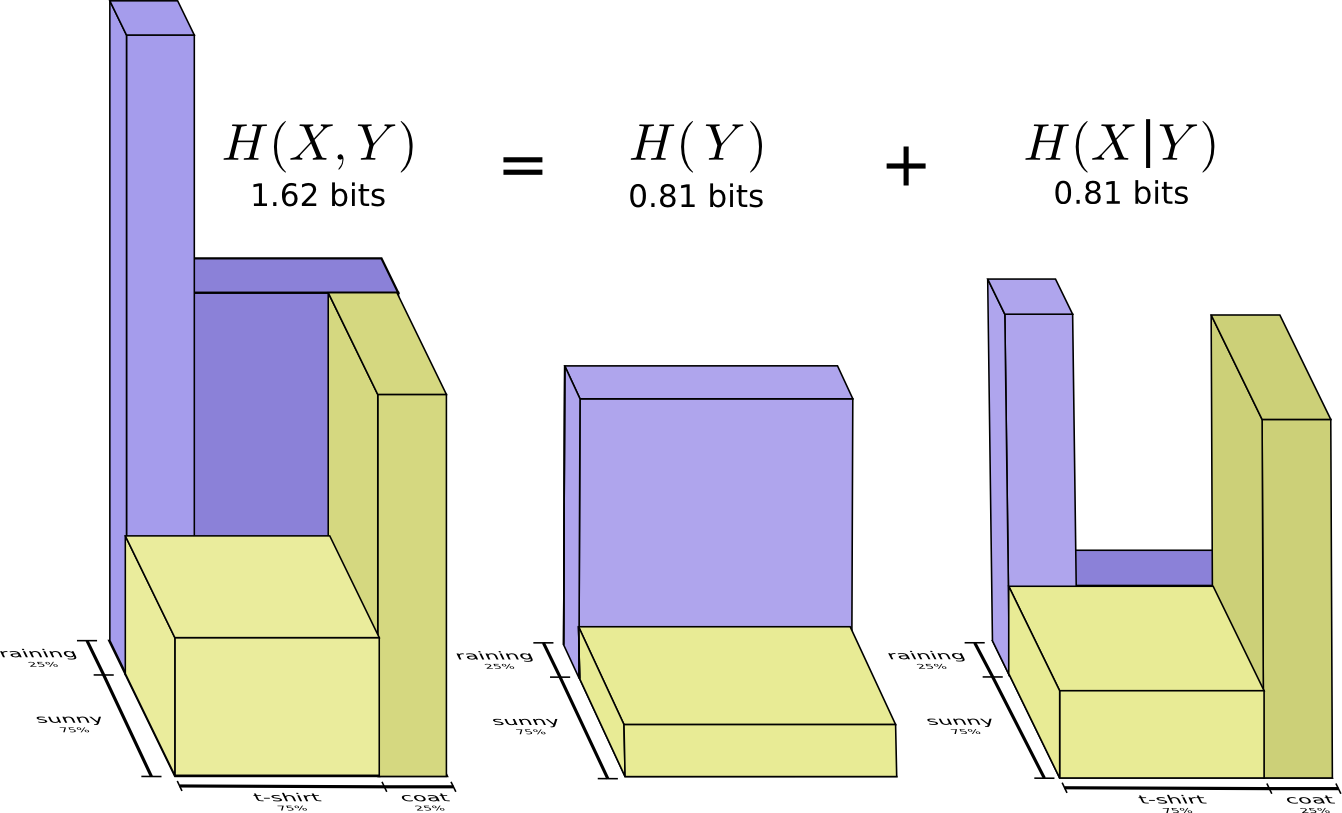
इसके बजाय, हम मौसम जैसे एक चर पर ध्यान केंद्रित करते हैं। हम धूप और बरसात के मौसम की संभावनाओं को जानते हैं। दोनों मामलों में, हम सशर्त संभावनाओं पर विचार कर सकते हैं। क्या संभावना है कि मैं सनी होने पर एक टी-शर्ट पहनूंगा? क्या संभावना है कि मैं बारिश होने पर रेनकोट पहन लूंगा?
25% की संभावना के साथ, बारिश होगी। यदि बारिश होती है, तो मैं 75% संभावना के साथ रेनकोट पहनूंगा। इस प्रकार, संभावना है कि बारिश हो रही है और मैं रेनकोट पहनता हूँ 75% का 25%, जो लगभग 19% है। संभावना यह है कि बारिश हो रही है और मैंने रेनकोट पहन रखा है, यह संभावना है कि यह इस संभावना से कई गुना अधिक बारिश हो रही है कि अगर बारिश हो रही है तो मैं रेनकोट पहनूंगा। हम इसे इस तरह लिखते हैं:
यह प्रायिकता सिद्धांत की सबसे मौलिक पहचानों में से एक है:
हम वितरण को दो-भाग वाले उत्पाद में तोड़कर कारक बनाते हैं। सबसे पहले, हम इस संभावना को देखते हैं कि एक चर, मौसम, एक निश्चित मूल्य पर ले जाएगा। फिर हम इस संभावना को देखते हैं कि एक और चर, मेरे कपड़े, पहले चर के कारण मूल्य पर ले जाएगा।
किस चर के साथ शुरू करना मायने नहीं रखता। हम अपने कपड़ों के साथ शुरुआत कर सकते हैं, और फिर इससे होने वाले मौसम को देख सकते हैं। यह कम सहज लग सकता है क्योंकि हम समझते हैं कि मौसम के बीच एक कारण संबंध है जो मुझे प्रभावित करता है कि मैं क्या पहनता हूं और इसके विपरीत नहीं ... लेकिन फिर भी यह काम करता है!
आइए एक उदाहरण देखें। यदि हम एक यादृच्छिक दिन चुनते हैं, तो 38% की संभावना के साथ मैं रेनकोट पहनूंगा। अगर हम जानते हैं कि मैं एक रेनकोट में हूं, तो बारिश होने की कितनी संभावना है? मैं बल्कि धूप में बारिश में रेनकोट पहनना चाहता हूं, लेकिन कैलिफोर्निया में बारिश दुर्लभ है, और यह पता चलता है कि 50% संभावना के साथ बारिश होगी। तो, संभावना यह है कि बारिश हो रही है और मैं रेनकोट पहनता हूं, इस बात की संभावना है कि मैं रेनकोट (38%) पहनूंगा, इस संभावना से कई गुना अधिक है कि अगर मैं रेनकोट (50%) पहनता हूं तो बारिश होगी लगभग 19%।
यह हमें उसी संभावना वितरण की कल्पना करने का दूसरा तरीका देता है।
कृपया ध्यान दें कि लेबल मान का पिछले आरेख की तुलना में थोड़ा अलग अर्थ है: एक टी-शर्ट और एक रेनकोट अब सीमा संभावनाएं हैं, संभावना है कि मैं इन कपड़ों को मौसम का ध्यान रखे बिना पहनूंगा। दूसरी ओर, अब दो बारिश और सूरज के निशान हैं, क्योंकि उनकी संभावनाएं इस तथ्य पर निर्भर करती हैं कि मैं एक टी-शर्ट या रेनकोट पहनूंगा।
(आपने बेयस के प्रमेय के बारे में सुना होगा। आप इसे संभाव्यता वितरण का प्रतिनिधित्व करने के इन दो अलग-अलग तरीकों के बीच संक्रमण के तरीके के रूप में कल्पना कर सकते हैं!)
बॉक्स: द सिम्पसन विरोधाभास
क्या संभावना वितरण के लिए ये दृश्य तकनीक वास्तव में उपयोगी हैं? मुझे ऐसा लगता है! थोड़ा आगे, हम उन्हें सूचना के सिद्धांत की कल्पना करने के लिए उपयोग करते हैं, लेकिन अब हम सिम्पसन विरोधाभास का अध्ययन करने के लिए उनका उपयोग करते हैं। सिम्पसन विरोधाभास एक अत्यंत अचूक सांख्यिकीय स्थिति है। सहज स्तर पर समझना मुश्किल है। माइकल नीलसन ने एक उत्कृष्ट निबंध
Reinventing Explanation लिखा, जो कई मायनों में विरोधाभास की व्याख्या करता है। मैं पिछले अनुभाग में विकसित की गई तकनीकों का उपयोग करके, इसे स्वयं करने की कोशिश करना चाहता हूं।
गुर्दे की पथरी के इलाज के दो तरीकों का परीक्षण किया जा रहा है। आधे मरीजों को उपचार ए प्राप्त होता है, जबकि अन्य आधे लोगों को उपचार बी प्राप्त होता है। जिन मरीजों को उपचार बी प्राप्त होता है, उन्हें ए बी प्राप्त करने वालों की तुलना में ठीक होने की अधिक संभावना होती है।
हालांकि, छोटे गुर्दे की पथरी वाले रोगियों को ठीक होने की अधिक संभावना थी यदि उन्हें उपचार प्राप्त होता है। गुर्दे में बड़े गुर्दे की पथरी वाले रोगियों को भी इलाज ए प्राप्त होने पर ठीक होने की अधिक संभावना थी! यह कैसे हो सकता है?
समस्या का सार यह है कि अध्ययन को ठीक से यादृच्छिक नहीं किया गया था। उपचार ए प्राप्त करने वाले रोगियों में, बड़े गुर्दे की पथरी वाले अधिक रोगी थे, और उपचार बी प्राप्त करने वाले रोगियों में छोटे गुर्दे की पथरी के साथ अधिक थे।
जैसा कि यह पता चला है, छोटे गुर्दे की पथरी वाले रोगियों में सामान्य रूप से ठीक होने की अधिक संभावना है।
इसे बेहतर ढंग से समझने के लिए, हम दो पिछले आरेखों को जोड़ सकते हैं। परिणाम एक छोटे और बड़े गुर्दे की पथरी में विभाजित वसूली दर के साथ एक तीन आयामी चार्ट है।
अब हम देखते हैं कि छोटे और बड़े दोनों तरह के पत्थरों के मामले में, उपचार A उपचार के लिए बेहतर है। B. उपचार B केवल इसलिए बेहतर लगता है क्योंकि जिन रोगियों पर यह लागू किया गया था, सामान्य तौर पर, ठीक होने की अधिक संभावना है!
कोड
अब जब हमारे पास संभाव्यता की कल्पना करने के तरीके हैं, तो हम सूचना के सिद्धांत में गोता लगा सकते हैं।
मैं आपको अपने काल्पनिक मित्र बॉब के बारे में बताता हूँ। बॉब जानवरों से बहुत प्यार करता है। वह लगातार जानवरों के बारे में बात करता है। वास्तव में, वह केवल चार शब्द बोलता है: "कुत्ता", "बिल्ली", "मछली" और "पक्षी"।
कुछ हफ़्ते पहले, इस तथ्य के बावजूद कि बॉब मेरी कल्पना का एक अवतार था, वह ऑस्ट्रेलिया चला गया। इसके अलावा, उन्होंने फैसला किया कि वह केवल द्विआधारी प्रारूप में संवाद करना चाहते थे। बॉब के मेरे सभी (काल्पनिक) संदेश इस प्रकार हैं:
संवाद करने के लिए, बॉब और मुझे एक कोडिंग सिस्टम बनाने की आवश्यकता है - बिट्स के अनुक्रम में शब्दों को प्रदर्शित करने का एक तरीका।
संदेश भेजने के लिए, बॉब प्रत्येक वर्ण (शब्द) को संबंधित कोड शब्द के साथ बदल देता है, फिर उन्हें एक साथ जोड़कर एक एन्कोडेड स्ट्रिंग बनाता है।
चर लंबाई कोड
दुर्भाग्य से, काल्पनिक ऑस्ट्रेलिया में संचार सेवाएं महंगी हैं। मुझे बॉब से प्राप्त होने वाले प्रत्येक संदेश के लिए मुझे $ 5 का भुगतान करना होगा। क्या मैंने उल्लेख किया है कि बॉब बहुत बात करना पसंद करते हैं? दिवालिया न होने के लिए, बॉब और मैंने यह पता लगाने का फैसला किया कि क्या यह संभव था कि किसी तरह संदेश की औसत लंबाई को कम किया जा सके।
यह पता चला है कि बॉब सभी शब्दों को समान रूप से अक्सर उच्चारण नहीं करता है। बॉब को कुत्तों से बहुत प्यार है। वह हर समय कुत्तों के बारे में बात करता है। कभी-कभी वह अन्य जानवरों के बारे में बात करता है - विशेष रूप से एक बिल्ली जिसे उसका कुत्ता पीछा करना पसंद करता है - लेकिन ज्यादातर वह कुत्तों के बारे में बात करता है। यहाँ उनके शब्दों की आवृत्ति का एक ग्राफ है:
यह उत्साहजनक है। हमारा पुराना कोड 2-बिट कोड शब्दों का उपयोग करता है, चाहे वे कितनी बार उपयोग किए जाएं।
यह कल्पना करने का एक अच्छा तरीका है। निम्नलिखित आरेख में, हम प्रत्येक शब्द की संभावना की कल्पना करने के लिए ऊर्ध्वाधर अक्ष का उपयोग करते हैं
और संबंधित कोडवर्ड की लंबाई का अनुमान लगाने के लिए एक क्षैतिज अक्ष
। कृपया ध्यान दें कि परिणामी क्षेत्र हमारे द्वारा भेजे गए कोड शब्द की औसत लंबाई है, इस मामले में 2 बिट्स।
हम होशियार हो सकते हैं और कोड को लंबाई में बना सकते हैं, जहां सामान्य शब्दों के लिए कोड शब्द छोटे किए जाते हैं। समस्या यह है कि कोडवर्ड के बीच प्रतिस्पर्धा है - कुछ छोटे बनाने से, हम दूसरों को लंबे समय तक बनाने के लिए मजबूर हैं। संदेश की लंबाई को कम करने के लिए, आदर्श रूप से हम चाहते हैं कि सभी कोड शब्द कम हों, लेकिन सबसे कम व्यापक रूप से उपयोग किए जाने चाहिए। इस प्रकार, परिणामी कोड में सामान्य शब्दों के लिए छोटे कोडवर्ड होते हैं (उदाहरण के लिए, "डॉग") और दुर्लभ शब्दों के लिए लंबे कोडवर्ड होते हैं (उदाहरण के लिए, "पक्षी")।
आइए फिर से इसकी कल्पना करें। कृपया ध्यान दें कि सबसे आम कोडवर्ड छोटे हैं और सबसे कम लंबे होते हैं। नतीजतन, हमें एक छोटा क्षेत्र मिला। यह एक छोटी अपेक्षित कोडवर्ड लंबाई से मेल खाती है। औसत कोडवर्ड की लंबाई अब 1.75 बिट्स है!
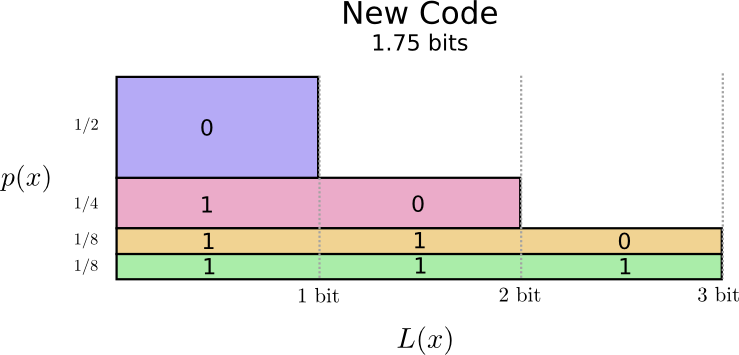
(आप आश्चर्यचकित हो सकते हैं: एक कोडवर्ड के रूप में अलग से 1 का उपयोग क्यों नहीं किया जाता है? दुर्भाग्य से, यह विस्फोट हो जाने पर अस्पष्टता का कारण होगा। हम बाद में इस बारे में अधिक बात करेंगे।
यह पता चला है कि यह कोड सबसे अच्छा संभव है। इस वितरण के लिए कोई कोड नहीं है जो हमें 1.75 बिट से कम की औसत कोडवर्ड लंबाई देगा।
एक मौलिक सीमा है। किस शब्द का प्रसारण कहा गया, इस वितरण की कौन सी घटना हुई, हमें औसतन कम से कम 1.75 बिट्स प्रसारित करने की आवश्यकता है। कोई फर्क नहीं पड़ता कि हमारा कोड कितना स्मार्ट हो सकता है, यह प्राप्त करना असंभव है कि औसत संदेश की लंबाई कम है। हम इस मूलभूत सीमा को
वितरण एन्ट्रापी कहते हैं - हम इसके बारे में नीचे विस्तार से चर्चा करेंगे।
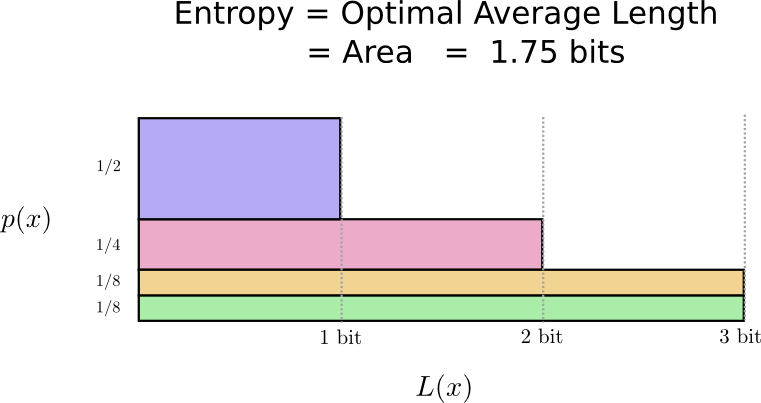
अगर हम इस सीमा को समझना चाहते हैं, तो हमें कुछ कोड शब्दों को छोटा और दूसरों को लंबे समय तक रखने के बीच के व्यापार को समझने की आवश्यकता है। एक बार जब हम यह पता लगा लेते हैं, तो हम यह पता लगा सकते हैं कि सबसे अच्छा संभव कोडिंग सिस्टम कैसा दिखता है।
कोडवर्ड स्पेस
1 बिट की लंबाई के साथ दो कोडवर्ड हैं: 0 और 1. 2 बिट्स की लंबाई के साथ चार कोडवर्ड हैं: 00, 01, 10 और 11. प्रत्येक बिट आप संभव कोडवर्ड की संख्या को दोगुना करते हैं।
हम चर-लंबाई कोड में रुचि रखते हैं, जहां कुछ कोड शब्द दूसरों की तुलना में लंबे होते हैं। जब हमारे पास आठ कोडवर्ड 3 बिट लंबे होते हैं, तो हम साधारण स्थिति में आ सकते हैं। अधिक जटिल मिश्रण हो सकते हैं, उदाहरण के लिए, लंबाई 2 के दो कोडवर्ड और लंबाई के चार कोडवर्ड 3. हम विभिन्न लंबाई के कितने कोडवर्ड तय कर सकते हैं?
याद रखें कि बॉब अपने संदेशों को एन्क्रिप्टेड स्ट्रिंग्स में बदल देता है, प्रत्येक शब्द को अपने कोड के साथ बदल देता है और उन्हें संक्षिप्त करता है।
चर-लंबाई कोड बनाते समय सावधान रहने के लिए एक सूक्ष्म सवाल है। कोड शब्दों में एन्कोडेड स्ट्रिंग को कैसे विभाजित करते हैं? जब सभी कोडवर्ड की लंबाई समान होती है, तो यह आसान होता है - बस स्ट्रिंग को उस लंबाई के टुकड़ों में विभाजित करें। लेकिन चूंकि विभिन्न लंबाई के कोडवर्ड हैं, इसलिए हमें सामग्री पर ध्यान देने की आवश्यकता है।
हम चाहते हैं कि हमारा कोड विशिष्ट रूप से डिकोडेबल हो। और हम नहीं चाहते कि यह निर्धारित करने में अस्पष्ट हो कि कौन से कोडवर्ड एन्कोडेड स्ट्रिंग बनाते हैं। यदि हमारे पास एक विशेष प्रतीक "कोड शब्द का अंत" है, तो यह सरल होगा। लेकिन हमारे पास ऐसा नहीं है - हम केवल 0 और 1 भेजते हैं। हमें कोड शब्दों के अनुक्रम को देखने और यह निर्धारित करने की आवश्यकता है कि उनमें से प्रत्येक कहाँ समाप्त होता है।
यह कोड बनाना बहुत सरल है जो कि स्पष्ट रूप से डिक्रिप्ट नहीं किया जा सकता है। उदाहरण के लिए, कल्पना करें कि 0 और 01 दोनों कोडवर्ड हैं। फिर यह स्पष्ट नहीं है कि लाइन 0100111 का पहला कोडवर्ड क्या है - यह या तो यह या वह हो सकता है! हमें जो संपत्ति चाहिए वह यह है कि यदि हम एक विशिष्ट कोडवर्ड को देखते हैं, तो उसे दूसरे, लंबे कोडवर्ड में शामिल नहीं किया जाना चाहिए। दूसरे शब्दों में, कोई भी कोडवर्ड दूसरे कोडवर्ड का उपसर्ग नहीं होना चाहिए। इसे प्रीफ़िक्स प्रॉपर्टी कहा जाता है, और जो कोड इसे मानते हैं, उन्हें
प्रीफ़िक्स कोड कहा जाता है।
इसका प्रतिनिधित्व करने का एक उपयोगी तरीका यह है कि प्रत्येक कोडवर्ड में संभावित कोडवर्ड के स्थान से बलिदान की आवश्यकता होती है। यदि हम कोड शब्द 01 को लेते हैं, तो हम किसी भी कोड शब्द का उपयोग करने की क्षमता खो देते हैं। अस्पष्टता के कारण हम अब 010 या 011010110 का उपयोग नहीं कर सकते हैं - वे हमारे लिए खो गए हैं।
चूंकि सभी कोडवर्ड का एक चौथाई 01 से शुरू होता है, इसलिए हमने सभी संभावित कोडवर्ड का एक चौथाई हिस्सा दान कर दिया। इस कीमत पर हम इस तथ्य के बदले में भुगतान करते हैं कि हमारे पास केवल 2 बिट्स की लंबाई के साथ एक कोडवर्ड है! बदले में, इस बलिदान का मतलब है कि अन्य सभी कोडवर्ड थोड़े लंबे होने चाहिए। अलग-अलग कोडवर्ड की लंबाई के बीच हमेशा एक तरह का समझौता होता है। एक छोटा कोडवर्ड आपको संभावित कोडवर्ड के अधिकांश स्थान का त्याग करने की आवश्यकता है, जो अन्य कोडवर्ड की संक्षिप्तता को रोकता है। हमें यह पता लगाने की आवश्यकता है कि सही तरीके से समझौता कैसे किया जाए!
इष्टतम कोडिंग
आप इसे एक सीमित बजट के रूप में सोच सकते हैं जिसे आप शॉर्ट कोड शब्द प्राप्त करने पर खर्च कर सकते हैं। हम एक कोडवर्ड के लिए भुगतान करते हैं, संभावित कोडवर्ड का हिस्सा बलिदान करते हैं।
लंबाई 0 के कोडवर्ड को खरीदने की लागत 1 है - सभी संभव कोडवर्ड - यदि आप लंबाई 0 का कोडवर्ड चाहते हैं, तो आपके पास कोई अन्य कोडवर्ड नहीं हो सकता है। 1 की लंबाई के साथ एक कोडवर्ड की लागत, उदाहरण के लिए, "0", 1/2 है, क्योंकि संभावित कोडवर्ड का आधा "0" से शुरू होता है। लंबाई 2 के कोडवर्ड की लागत, उदाहरण के लिए "01", 1/4 है, क्योंकि सभी संभावित कोडवर्ड का एक चौथाई "01" से शुरू होता है। सामान्य तौर पर, कोडवर्ड की बढ़ती लंबाई के साथ कोडवर्ड की लागत तेजी से घट जाती है।
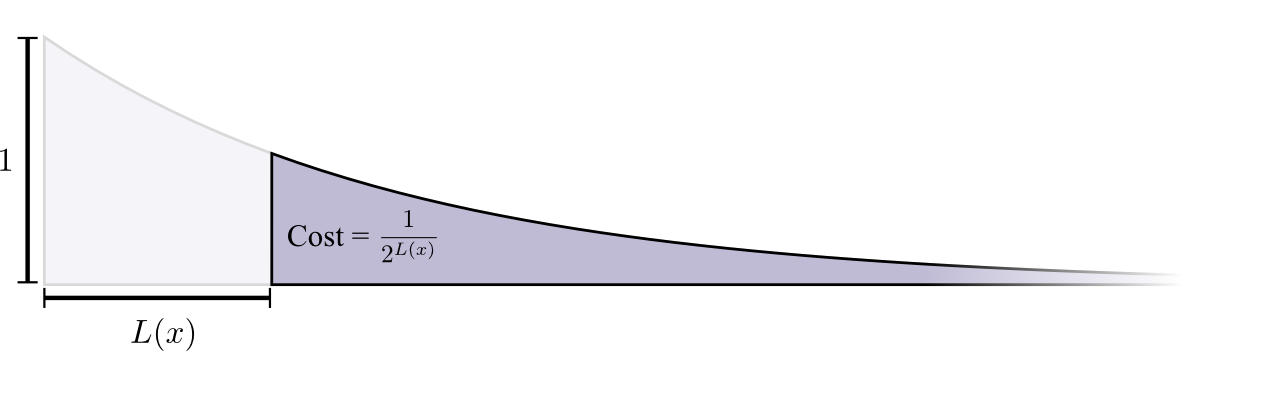
कृपया ध्यान दें कि यदि लागत एक (इन-तरह) प्रदर्शक के रूप में घटती है, तो यह ऊंचाई और क्षेत्र दोनों है! (
उदाहरण ने बेस 2 के साथ एक घातांक का उपयोग किया जहां यह तथ्य गलत है, लेकिन आप प्राकृतिक घातांक पर स्विच कर सकते हैं, जो नेत्रहीन प्रमाण को सरल करता है। )
हमें लघु कोडवर्ड की आवश्यकता है क्योंकि हम औसत संदेश लंबाई कम करना चाहते हैं। प्रत्येक कोडवर्ड उस शब्द समय की लंबाई द्वारा औसत संदेश लंबाई बढ़ाता है। उदाहरण के लिए, यदि हमें किसी कोडवर्ड को ४ बिट्स लंबे समय के ५०% भेजने की आवश्यकता है, तो हमारी औसत संदेश लंबाई २ बिट्स से अधिक होगी यदि हमने यह कोडवर्ड नहीं भेजा था। हम इसे एक आयत के रूप में कल्पना कर सकते हैं।
ये दोनों मूल्य कोडवर्ड लंबाई से संबंधित हैं। हमारे द्वारा भुगतान की जाने वाली कीमत कोड शब्द की लंबाई निर्धारित करती है। कोडवर्ड की लंबाई निर्धारित करती है कि यह संदेश की औसत लंबाई में कितना जोड़ता है। हम उन्हें इस तरह एक साथ कल्पना कर सकते हैं।

लघु कोडवर्ड औसत संदेश की लंबाई को कम करते हैं, लेकिन महंगे होते हैं, जबकि लंबे कोडवर्ड औसत संदेश की लंबाई बढ़ाते हैं, लेकिन सस्ते होते हैं।

हमारे सीमित बजट का उपयोग करने का सबसे अच्छा तरीका क्या है? प्रत्येक घटना के लिए हमें एक कोडवर्ड पर कितना खर्च करना चाहिए?
जिस तरह एक व्यक्ति उन उपकरणों में अधिक निवेश करना चाहता है जो वह नियमित रूप से उपयोग करता है, हम आमतौर पर इस्तेमाल किए गए कोड शब्दों पर अधिक खर्च करना चाहते हैं। ऐसा करने के लिए एक विशेष रूप से प्राकृतिक तरीका है: हमारे बजट को घटना के कितनी बार होने के अनुपात में वितरित करें। इसलिए, यदि कोई घटना 50% मामलों में होती है, तो हम अपने बजट का 50% इसके लिए एक शॉर्ट कोड शब्द खरीदने पर खर्च करते हैं। लेकिन अगर घटना केवल 1% होती है, तो हम अपने बजट का केवल 1% खर्च करते हैं, क्योंकि हम कोड शब्द की लंबाई के बारे में बहुत चिंतित नहीं हैं।
यह एक बहुत ही स्वाभाविक बात है, लेकिन क्या यह इष्टतम है? यह ऐसा है, और मैं इसे साबित करूंगा!
निम्नलिखित प्रमाण स्पष्ट है और इसे समझा जाना चाहिए, लेकिन इसे बाहर करने के लिए कुछ काम करना होगा, और यह निश्चित रूप से इस निबंध का सबसे कठिन हिस्सा है। पाठक इसे बिना किसी सबूत के तथ्य को स्वीकार करते हुए सुरक्षित रूप से छोड़ सकते हैं और अगले भाग पर जा सकते हैं।, , .
,
. , ,
और
।
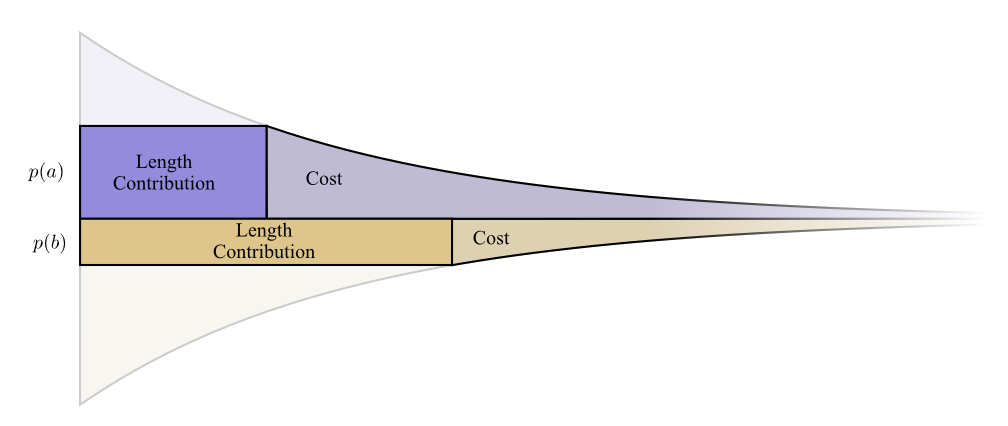
. - ?
, , . , , .

,
। , , .
—
। , ,
।
, . , : , . , , / — , .
, . p(a) — . . / , .
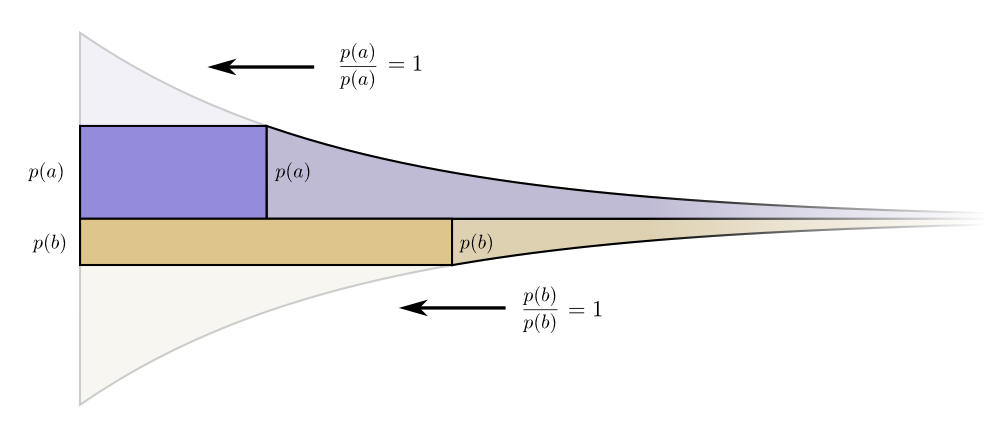
, . , . , , .
,
।
,
.
,
। . , /
, . , / b
, .
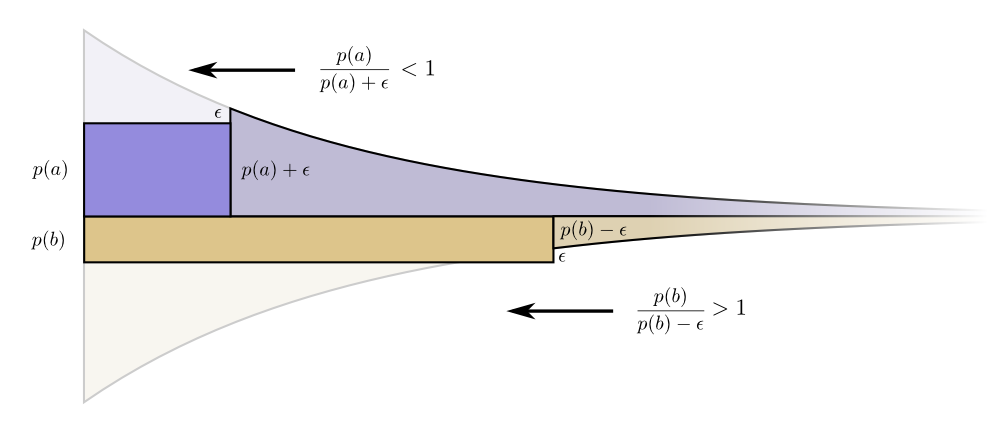
.
,
। : «
!
!» . .
— , , — , . ( , .)
( , , , , . ? , , , . , , , !)
PS , -, , .