SVM। अजगर में खरोंच और कार्यान्वयन से स्पष्टीकरण। समर्थन वेक्टर विधि का विस्तृत विश्लेषण

एमएल-समुराई का रास्ता चुनने वाले सभी को नमस्कार!

परिचय:

इस आलेख में, हम वर्गीकरण समस्या के लिए समर्थन वेक्टर मशीन विधि ( Eng। SVM, समर्थन वेक्टर मशीन ) पर विचार करते हैं। एल्गोरिथ्म का मुख्य विचार प्रस्तुत किया जाएगा, इसके भार को स्थापित करने का आउटपुट और एक सरल DIY कार्यान्वयन का विश्लेषण किया जाएगा। एक डाटासेट के उदाहरण पर $$$आइरिस$अंतरिक्ष में रैखिक रूप से वियोज्य / अविभाज्य डेटा के साथ लिखित एल्गोरिदम के संचालन का प्रदर्शन किया जाएगा $$$R ^ 2$और प्रशिक्षण / पूर्वानुमान का दृश्य। इसके अलावा, एल्गोरिथ्म के पेशेवरों और विपक्ष, इसके संशोधनों की घोषणा की जाएगी।

चित्र 1. एक आईरिस फूल की ओपन सोर्स फोटो

हल की जाने वाली समस्या:

हम बाइनरी की समस्या को हल करेंगे (जब केवल दो वर्ग हैं) वर्गीकरण। सबसे पहले, एल्गोरिथ्म प्रशिक्षण सेट से वस्तुओं पर ट्रेन करता है, जिसके लिए वर्ग लेबल पहले से जाना जाता है। इसके अलावा, पहले से ही प्रशिक्षित एल्गोरिथ्म प्रत्येक ऑब्जेक्ट के लिए वर्ग लेबल को आस्थगित / परीक्षण नमूने से भविष्यवाणी करता है। क्लास लेबल मान ले सकते हैं $$$Y = \ {- 1, +1 \}$ । ऑब्जेक्ट - एन संकेतों के साथ वेक्टर $$$x = (x_1, x_2, ..., x_n)$अंतरिक्ष में $$$आर ^ एन$। सीखते समय, एल्गोरिथ्म को एक फ़ंक्शन का निर्माण करना चाहिए $$$F (x) = y$जो एक तर्क लेता है $$$x$- अंतरिक्ष से कोई वस्तु $$$आर ^ एन$और वर्ग लेबल देता है $$$य$।

एल्गोरिथ्म के बारे में सामान्य शब्द:

वर्गीकरण कार्य एक शिक्षक के साथ शिक्षण से संबंधित है। एसवीएम एक शिक्षक के साथ एक सीखने का एल्गोरिथ्म है। नेत्रहीन, कई मशीन लर्निंग एल्गोरिदम इस शीर्ष लेख में पाया जा सकता है ("मशीन सीखने की दुनिया का नक्शा" अनुभाग देखें)। यह जोड़ा जाना चाहिए कि एसवीएम का उपयोग प्रतिगमन समस्याओं के लिए भी किया जा सकता है, लेकिन इस लेख में एसवीएम क्लासिफायर का विश्लेषण किया जाएगा।

एक वर्गीकरणकर्ता के रूप में एसवीएम का मुख्य लक्ष्य एक अलग हाइपरप्लेन के समीकरण को खोजना है
$$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 = 0$अंतरिक्ष में $$$आर ^ एन$, जो दो वर्गों को कुछ इष्टतम तरीके से विभाजित करेगा। परिवर्तन का सामान्य दृश्य $$$एफ$वस्तु $$$x$वर्ग लेबल के लिए $$$य$: $$$F (x) = साइन (w ^ Tx-b)$। हम याद रखेंगे कि हमने नामित किया है $$$w = (w_1, w_2, ..., w_n), b = -w_0$। एल्गोरिथ्म वजन सेट करने के बाद $$$w$और $$$ब$(प्रशिक्षण), निर्मित हाइपरप्लेन के एक तरफ गिरने वाली सभी वस्तुओं को पहले वर्ग के रूप में और दूसरी तरफ गिरने वाली वस्तुओं के बारे में भविष्यवाणी की जाएगी।

अंदर का कार्य $$$चिन्ह ()$एल्गोरिथ्म वज़न के साथ ऑब्जेक्ट की सुविधाओं का एक रैखिक संयोजन है, यही वजह है कि एसवीएम रैखिक एल्गोरिदम को संदर्भित करता है। एक विभाजित हाइपरप्लेन का निर्माण विभिन्न तरीकों से किया जा सकता है, लेकिन एसवीएम वेट में $$$w$और $$$ब$कॉन्फ़िगर किया गया है ताकि क्लास ऑब्जेक्ट्स अलग-अलग हाइपरप्लेन से जितना संभव हो सके दूर रहें। दूसरे शब्दों में, एल्गोरिथ्म हाइपरप्लेन और क्लास ऑब्जेक्ट्स के बीच अंतर ( अंग्रेजी मार्जिन ) को अधिकतम करता है जो इसके सबसे करीब हैं। ऐसी वस्तुओं को समर्थन वैक्टर कहा जाता है (चित्र 2 देखें)। इसलिए एल्गोरिथ्म का नाम।

चित्रा 2. एसवीएम ( यहां से आंकड़े का आधार)

SVM स्केल समायोजन नियमों का एक विस्तृत आउटपुट:

नमूना बिंदुओं से जहां तक ​​संभव हो डिवाइडर हाइपरप्लेन रखने के लिए, स्ट्रिप की चौड़ाई अधिकतम होनी चाहिए। वेक्टर $$$w$डिवाइडिंग हाइपरप्लेन का निर्देशन वेक्टर है। इसके बाद, हम दो वैक्टर के स्केलर उत्पाद को निरूपित करते हैं $$$\ langle a, b \ rangle$या $$$ए ^ टीबी$.Let वेक्टर के प्रोजेक्शन का पता लगाएं, जिसके सिरों पर हाइपरप्लेन के दिशा वेक्टर पर विभिन्न वर्गों के समर्थन वैक्टर होंगे। यह प्रक्षेपण विभाजन पट्टी की चौड़ाई दिखाएगा (चित्र 3 देखें):

चित्रा 3. तराजू स्थापित करने के लिए नियमों का उत्पादन ( यहां से आंकड़े का आधार)

कक्षा की सीमा से ऑब्जेक्ट x का मार्जिन मान है $$$M = y (w ^ Tx-b)$। एल्गोरिथ्म ऑब्जेक्ट पर एक त्रुटि बनाता है अगर और केवल अगर इंडेंट $$$एम$नकारात्मक (जब $$$य$और $$$(w ^ Tx-b)$अलग-अलग पात्र)। अगर $$$M 0 (0, 1)$, फिर वस्तु विभाजन पट्टी के अंदर आती है। अगर $$$M> 1$, तब ऑब्जेक्ट x को सही ढंग से वर्गीकृत किया गया है, और विभाजन पट्टी से कुछ दूरी पर स्थित है। हम इस संबंध को लिखते हैं:

परिणामी प्रणाली हार्ड-मार्जिन एसवीएम के साथ डिफ़ॉल्ट एसवीएम सेटिंग है, जब किसी ऑब्जेक्ट को जुदाई बैंड में प्रवेश करने की अनुमति नहीं है। इसे कुहन-टकर प्रमेय के माध्यम से विश्लेषणात्मक रूप से हल किया गया है। परिणामी समस्या लैगरेंज फ़ंक्शन की काठी बिंदु खोजने की दोहरी समस्या के बराबर है।

$$$ $ $ $ $ \ बायाँ {\ _ \ _ शुरू {सरणी} {ll} (w ^ ट्व) / 2 \ n सहीरा मिनट और \ textrm {} \\ y (w ^ Tx-b) \ geqslant 1 & textrm {} \ end {सरणी} \ सही। $ $ प्रदर्शन $ $

यह सब तब तक अच्छा है जब तक हमारी कक्षाएं रैखिक रूप से अलग होने योग्य हैं। ताकि एल्गोरिथ्म रैखिक रूप से अविभाज्य डेटा के साथ काम कर सके, चलो हमारे सिस्टम को थोड़ा बदल दें। एल्गोरिथ्म को प्रशिक्षण वस्तुओं पर गलतियाँ करने दें, लेकिन साथ ही कम त्रुटियों को रखने की कोशिश करें। हम अतिरिक्त चर का एक सेट पेश करते हैं $$$\ xi _i> 0$प्रत्येक वस्तु पर त्रुटि की भयावहता का वर्णन करना $$$x_i$। हम न्यूनतम कार्यात्मक में कुल त्रुटि के लिए एक दंड पेश करते हैं:

$$$ $ $ $ $ \ बायाँ {\ _ शुरू करना {सरणी} {ll} (w ^ ट्व) / 2 + \ अल्फा \ योग \ xi _i \ rightarrow मिनट और \ textrm {} \\ y (w ^ Tx_i-b) \ geqllant 1 - \ xi _i & \ textrm {} \\ \ xi _i \ geqslant0 & \ textrm {} \ end {सरणी} \ right। $ $ प्रदर्शन $ $

हम एल्गोरिथ्म त्रुटियों की संख्या पर विचार करेंगे (जब एम <0)। इसे दंड कहो। तब सभी वस्तुओं के लिए जुर्माना प्रत्येक वस्तु के लिए जुर्माना की राशि के बराबर होगा $$$x_i$जहाँ $$$[M_i <0]$- थ्रेशोल्ड फ़ंक्शन (चित्र 4 देखें):

$$$ $ प्रदर्शन $ $ [M_i <0] = \ left \ {\ {शुरू {सरणी} {ll} 1 & \ textrm {अगर} M_i <0 \\ 0 & \ textrm {अगर} M_i \ geqrlant 0 \ end {सरणी} \ सही। $ $ प्रदर्शन $ $

अगला, हम दंड को त्रुटि के परिमाण के प्रति संवेदनशील बनाते हैं और साथ ही साथ वस्तु को कक्षा की सीमा के निकट ले जाने के लिए दंड देते हैं:

दंड अभिव्यक्ति को जोड़ते समय शब्द $$$\ अल्फा (w ^ ट्व) / 2$हम एक वस्तु के लिए नरम अंतर ( सॉफ्ट-मार्जिन एसवीएम ) के साथ क्लासिक एसवीएम हानि फ़ंक्शन प्राप्त करते हैं:

$$$क्यू$- फंक्शन फंक्शन, यह एक लॉस फंक्शन भी है। यही हम हाथों के कार्यान्वयन में ढाल वंश की मदद से कम से कम करेंगे। हम बदलते वजन के नियमों को प्राप्त करते हैं, जहां $$$\ eta$- वंश कदम:

$$$ $ $ $ $ $ \ _ \ _ \ _trangledownown क्यू = \ \ \ {शुरू {सरणी} {ll} \ अल्फा w- yx & \ textrm {if} yw ^ Tx <1 \\ \ अल्फा w & \ textrm {if} yw ^ Tx \ geqslant 1 \ end {व्यू} सही। $ $ प्रदर्शन $ $

साक्षात्कार में संभावित प्रश्न (वास्तविक घटनाओं पर आधारित):

SVM के बारे में सामान्य प्रश्नों के बाद: Hinge_loss अधिकतम निकासी क्यों है? - सबसे पहले, याद रखें कि जब वजन बदलता है तो एक हाइपरप्लेन अपनी स्थिति बदल देता है $$$w$और $$$ब$। एल्गोरिथ्म का वजन तब बदलना शुरू होता है जब नुकसान फ़ंक्शन के ग्रेडिएंट शून्य के बराबर नहीं होते हैं (वे आमतौर पर कहते हैं: "ग्रेडिएंट प्रवाह)"। इसलिए, हमने विशेष रूप से एक ऐसी हानि फ़ंक्शन का चयन किया, जिसमें ग्रेडर सही समय पर प्रवाह करना शुरू कर देता है। $$$काज नुकसान$इस तरह दिखता है: $$$H = अधिकतम (0,1-y (w ^ Tx))$। याद रखें कि निकासी $$$m = y (w ^ Tx)$। जब अंतराल $$$एम$काफी बड़ा ( $$$1$या अधिक) अभिव्यक्ति $$$(1-m)$शून्य से कम हो जाता है और $$$H = 0$(इसलिए, ग्रेडिएंट प्रवाहित नहीं होते हैं और एल्गोरिथ्म का भार किसी भी तरह से नहीं बदलता है)। यदि अंतर मीटर पर्याप्त रूप से छोटा है (उदाहरण के लिए, जब ऑब्जेक्ट जुदाई बैंड और / या नकारात्मक में गिर जाता है (यदि वर्गीकरण का पूर्वानुमान गलत है), तो Hinge_loss सकारात्मक हो जाता है ( $$$H> 0$), ग्रेडिएंट प्रवाहित होने लगते हैं और एल्गोरिथ्म वज़न बदल जाता है। संक्षेप: ग्रेडिएंट्स दो मामलों में प्रवाहित होते हैं: जब सैंपल ऑब्जेक्ट जुदाई बैंड के अंदर गिर जाता है और जब ऑब्जेक्ट गलत तरीके से वर्गीकृत किया जाता है।

एक विदेशी भाषा के स्तर की जांच करने के लिए, समान प्रश्न संभव हैं: लॉजिस्टिक रीवेरियन और एसवीएम के बीच समानताएं और अंतर क्या हैं? - सबसे पहले, हम समानता के बारे में बात करेंगे: दोनों एल्गोरिदम पर्यवेक्षित सीखने में रैखिक वर्गीकरण एल्गोरिदम हैं। कुछ समानताएँ नुकसान कार्यों के उनके तर्क में हैं: $$$लॉग (1 + exp (-y (w ^ Tx)))$logreg के लिए और $$$अधिकतम (0,1-y (w ^ Tx))$SVM के लिए (चित्र 4 देखें)। दोनों एल्गोरिदम हम ग्रेडिएंट डीसेंट का उपयोग करके कॉन्फ़िगर कर सकते हैं। आगे हम मतभेदों के बारे में बात करते हैं: एसवीएम लॉगरेज के विपरीत ऑब्जेक्ट का क्लास लेबल, जो क्लास सदस्यता की संभावना लौटाता है। SVM क्लास लेबल के साथ काम नहीं कर सकता है $$$\ {0,1 \}$ (नाम बदलने वाली कक्षाओं के बिना) LogReg (LogReg loss fination) के विपरीत $$$\ {0,1 \}$ : $$$-लॉग (पी) - (1-वाई) लॉग (1-पी)$, कहाँ $$$य$- वास्तविक कक्षा लेबल, $$$पी$- एल्गोरिथ्म की वापसी, संबंधित वस्तु की संभावना $$$x$कक्षा के लिए $$$\ {1 \}$ )। इससे अधिक, हम ग्रेडिएंट डिसेंट के बिना हार्ड-मार्जिन एसवीएम समस्या को हल कर सकते हैं। सपोर्ट वैक्टर को खोजने का कार्य लैग्रेग फ़ंक्शन में काठी बिंदु की खोज के लिए कम हो गया है - यह कार्य केवल द्विघात प्रोग्रामिंग को संदर्भित करता है।

import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 

चित्रा 4. नुकसान के कार्य

क्लासिक सॉफ्ट-मार्जिन एसवीएम का सरल कार्यान्वयन:

चेतावनी! आपको लेख के अंत में पूर्ण कोड का लिंक मिलेगा। नीचे संदर्भ से बाहर निकाले गए कोड के ब्लॉक हैं। कुछ ब्लॉक केवल पिछले ब्लॉकों को काम करने के बाद शुरू किया जा सकता है। कई ब्लॉकों के तहत, चित्र रखे जाएंगे जो दिखाते हैं कि इसके ऊपर रखा कोड कैसे काम करता है।

 import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): #    #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l 

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended class CustomSVM(object): __class__ = "CustomSVM" __doc__ = """ This is an implementation of the SVM classification algorithm Note that it works only for binary classification ############################################################# ###################### PARAMETERS ###################### ############################################################# etha: float(default - 0.01) Learning rate, gradient step alpha: float, (default - 0.1) Regularization parameter in 0.5*alpha*||w||^2 epochs: int, (default - 200) Number of epochs of training ############################################################# ############################################################# ############################################################# """ def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) def predict(self, X:np.array) -> np.array: y_pred = [] X_extended = add_bias_feature(X) for i in range(len(X_extended)): y_pred.append(np.sign(np.dot(self._w,X_extended[i]))) return np.array(y_pred) def hinge_loss(self, x, y): return max(0,1 - y*np.dot(x, self._w)) def soft_margin_loss(self, x, y): return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) 

हम लाइनों के प्रत्येक ब्लॉक के संचालन पर विस्तार से विचार करते हैं:

1) एक फ़ंक्शन add_bias_feature (a ) बनाएं, जो प्रत्येक वेक्टर के नंबर 1 को जोड़ते हुए स्वचालित रूप से ऑब्जेक्ट्स के वेक्टर को बढ़ाता है। फ्री टर्म b के बारे में "भूल" करने के लिए यह आवश्यक है। अभिव्यक्ति $$$w ^ Tx-b$अभिव्यक्ति के बराबर $$$w_1x_1 + w_2x_2 + ... + w_nx_n + w_0 * 1$। हम सशर्त रूप से मानते हैं कि यूनिट सभी वैक्टर x, और के लिए वेक्टर का अंतिम घटक है $$$w_0 = -b$। अब वेट सेट कर रहे हैं $$$w$और $$$w_0$हम एक ही समय में उत्पादन करेंगे।

 def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended 

2) फिर हम क्लासिफायर का ही वर्णन करते हैं। इसमें इनिट को इनिशियलाइज़ करना () , लर्निंग फिट () , प्रेडिक्टिंग प्रेडिक्ट () , हिंग_लॉस () फंक्शन के नुकसान का पता लगाना और क्लासिकल एल्गोरिथम के फंक्शन का टोटल लॉस को सॉफ्ट गैप soft_margin -loss () से ढूंढना है ।

3) आरंभीकरण पर, 3 हाइपरपैरामीटर प्रस्तुत किए जाते हैं: _था - ढाल वंश का चरण ( $$$\ eta$), _ल्पा - आनुपातिक वजन में कमी की गति का गुणांक (नुकसान फ़ंक्शन में द्विघात से पहले) $$$\ अल्फा$), _epochs - प्रशिक्षण युग की संख्या।

  def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None 

4) प्रशिक्षण नमूने के प्रत्येक युग के लिए प्रशिक्षण के दौरान (X_train, Y_train) हम नमूना से एक तत्व लेंगे, इस तत्व और हाइपरप्लेन की स्थिति के बीच एक निश्चित समय पर अंतर की गणना करें। इसके अलावा, इस अंतर के आकार के आधार पर, हम नुकसान फ़ंक्शन के ग्रेडिएंट का उपयोग करके एल्गोरिथ्म के वजन को बदल देंगे $$$क्यू$। एक ही समय में, हम प्रत्येक युग के लिए इस फ़ंक्शन के मूल्य की गणना करेंगे और कितनी बार प्रति सप्ताह वज़न बदलेंगे। प्रशिक्षण शुरू करने से पहले, हम यह सुनिश्चित करेंगे कि दो अलग-अलग श्रेणी के लेबल वास्तव में सीखने के कार्य में नहीं आए हैं। संतुलन स्थापित करने से पहले, सामान्य वितरण का उपयोग करके इसे प्रारंभ किया जाता है।

  def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: #   self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: #         0<m<1 self._w = self._w +\ self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) 

लिखित एल्गोरिदम के संचालन की जाँच:

जांचें कि हमारा लिखित एल्गोरिदम कुछ प्रकार के खिलौना डेटा सेट पर काम करता है। आइरिस डेटासेट लें। हम डेटा तैयार करेंगे। कक्षा 1 और 2 को निरूपित करें $$$+ 1$, और कक्षा 0 के रूप में $$$-1$। पीसीए एल्गोरिथ्म (स्पष्टीकरण और यहां आवेदन) का उपयोग करते हुए, हम न्यूनतम डेटा हानि के साथ 4 विशेषताओं के स्थान को 2 तक कम कर देते हैं (यह प्रशिक्षण और परिणाम का निरीक्षण करना हमारे लिए आसान होगा)। अगला, हम एक प्रशिक्षण (ट्रेन) के नमूने और एक विलंबित (सत्यापन) में विभाजित करेंगे। हम प्रशिक्षण नमूने पर प्रशिक्षण देंगे, आस्थगित पर भविष्यवाणी और जाँच करेंगे। हम सीखने के कारकों को चुनते हैं ताकि नुकसान फ़ंक्शन गिर जाए। प्रशिक्षण के दौरान, हम प्रशिक्षण के नुकसान के कार्य और विलंबित नमूने को देखेंगे।

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

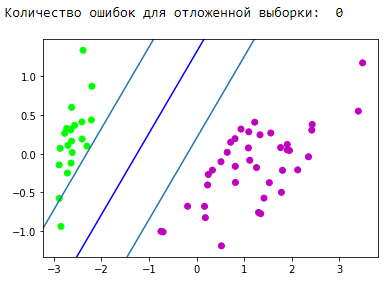
बहुत बढ़िया! हमारे एल्गोरिथ्म ने रैखिक रूप से वियोज्य डेटा को संभाला। अब इसे कक्षा 2 से अलग 0 और 1 को अलग करें:

 #    iris = load_iris() X = iris.data Y = iris.target pca = PCA(n_components=2) X = pca.fit_transform(X) Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1] X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) 

 #     svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300) svm.fit(X_train, Y_train, X_test, Y_test) print(svm.train_errors[:150]) # numbers of error in each epoch print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0 plt.plot(svm.train_loss, linewidth=2, label='train_loss') plt.plot(svm.val_loss, linewidth=2, label='test_loss') plt.grid() plt.legend(prop={'size': 15}) plt.show() 

 d = {-1:'green', 1:'red'} plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') #  w0*x_i[0]+w1*x_i[1]+w2*1=0  #  x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

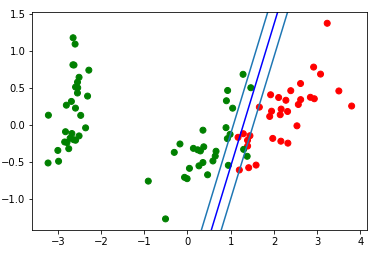
आइए जिफ़ को देखें, जो यह दिखाएगा कि प्रशिक्षण के दौरान विभाजित लाइन ने अपनी स्थिति कैसे बदल दी (केवल 500 फ्रेम बदलते वजन के लिए। पंक्ति में पहला 300। प्रत्येक 130 वें फ्रेम के लिए अगले 200 टुकड़े)।

 import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 return im fig = plt.figure() ims = [] for i in range(500): if i<=300: k = i else: k = (i-298)*130 im = one_image(svm.history_w[k], X_train, Y_train) ims.append([im]) ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True, repeat_delay=500) writer = PillowWriter(fps=20) ani.save("my_demo.gif", writer='imagemagick') 

 #    y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error print('    : ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 

रिक्त स्थान

यह समझना महत्वपूर्ण है कि वास्तविक समस्याओं में रैखिक रूप से वियोज्य डेटा के साथ एक साधारण मामला नहीं होगा। ऐसे डेटा के साथ काम करने के लिए, किसी अन्य स्थान पर जाने का विचार प्रस्तावित किया गया था, जहां डेटा रैखिक रूप से अलग होगा। ऐसे स्थान को सुधारक कहा जाता है। इस लेख में रेक्टिफाइंग स्पेस और कर्नेल प्रभावित नहीं होंगे। आप ई। सोकोलोव के 14,15,16 सिनॉप्सिस में और के.वी. वोर्त्सोव के व्याख्यानों में सबसे पूर्ण गणितीय सिद्धांत पा सकते हैं।

Sklearn से SVM ​​का उपयोग करना:

वास्तव में, लगभग सभी क्लासिक मशीन लर्निंग एल्गोरिदम आपके लिए लिखे गए हैं। चलो कोड का एक उदाहरण देते हैं, हम स्केलेर लाइब्रेरी से एल्गोरिथ्म लेंगे ।

 from sklearn import svm from sklearn.metrics import recall_score C = 1.0 # = self._alpha in our algorithm model1 = svm.SVC(kernel='linear', C=C) #model1 = svm.LinearSVC(C=C, max_iter=10000) #model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C) #model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C) model1.fit(X_train, Y_train) y_predict = model1.predict(X_test) print(recall_score(Y_test, y_predict, average=None)) 

क्लासिक एसवीएम के पेशेवरों और विपक्ष:

पेशेवरों:

1. बड़ी सुविधा स्थान के साथ अच्छी तरह से काम करता है;
2. छोटे डेटा के साथ अच्छी तरह से काम करता है;
3. इसलिए एल्गोरिथ्म डिवाइडिंग बैंड को अधिकतम करता है, जो एक एयरबैग की तरह, वर्गीकरण त्रुटियों की संख्या को कम कर सकता है;
4. चूंकि एल्गोरिथ्म एक उत्तल डोमेन में द्विघात प्रोग्रामिंग समस्या को हल करने के लिए कम कर देता है, इस तरह की समस्या का हमेशा एक अनूठा समाधान होता है (एल्गोरिथ्म के कुछ हाइपरपैरमीटर के साथ हाइपरप्लेन को अलग करना हमेशा समान होता है)।

विपक्ष:

1. लंबे प्रशिक्षण समय (बड़े डेटा सेट के लिए);
2. शोर अस्थिरता: प्रशिक्षण डेटा में आउटलेयर संदर्भ घुसपैठिया वस्तु बन जाते हैं और सीधे एक अलग हाइपरप्लेन के निर्माण को प्रभावित करते हैं;
3. वर्ग के रैखिक अविभाज्यता के मामले में एक विशेष समस्या के लिए सबसे उपयुक्त गुठली बनाने और रिक्त स्थान बनाने की सामान्य विधियां वर्णित नहीं हैं। उपयोगी डेटा परिवर्तनों का चयन करना एक कला है।

एसवीएम आवेदन:

एक या दूसरे मशीन लर्निंग एल्गोरिदम की पसंद सीधे डेटा खनन के दौरान प्राप्त जानकारी पर निर्भर करती है। लेकिन सामान्य शब्दों में, निम्नलिखित कार्यों को प्रतिष्ठित किया जा सकता है:

• एक छोटे डेटा सेट के साथ कार्य;
• पाठ वर्गीकरण कार्य। SVM एक अच्छी बेसलाइन ([प्रीप्रोसेसिंग] + [TF-iDF] + [SVM]) देता है, प्राप्त पूर्वानुमान सटीकता कुछ दृढ़ / आवर्तक तंत्रिका नेटवर्क के स्तर पर निकलती है (मैं इस सामग्री को समेकित करने के लिए खुद को आज़माने की सलाह देता हूं)। एक उत्कृष्ट उदाहरण यहां दिया गया है, "भाग 3. हम जो सिखाते हैं उनमें से एक का एक उदाहरण" ;
• संरचित डेटा वाले कई कार्यों के लिए, लिंक [फीचर इंजीनियरिंग] + [एसवीएम] + [कर्नेल] "स्टिल केक";
• चूँकि हिंग नुकसान को बहुत तेज़ माना जाता है, यह वौपाल वेबिट (डिफ़ॉल्ट रूप से) में पाया जा सकता है।

एल्गोरिथ्म संशोधनों:

सपोर्ट वेक्टर विधि में विभिन्न परिवर्धन और संशोधन हैं, जिसका उद्देश्य कुछ नुकसान को दूर करना है:

• प्रासंगिक वेक्टर मशीन (आरवीएम)
• 1-मानक SVM (LASSO SVM)
• नियमित रूप से SVM ​​(ElasticNet SVM)
• समर्थन सुविधाएँ मशीन (SFM)
• प्रासंगिकता मशीन (RFM)

SVM पर अतिरिक्त स्रोत:

1. के.वी. वोर्त्सोव द्वारा पाठ व्याख्यान
2. ई। सोकोलोव का सारांश - 14.15.16
3. अलेक्जेंड्रे कॉवेल्स्की द्वारा कूल स्रोत
4. एक हब्र पर svm को समर्पित 2 लेख हैं:
   
   • 2010 का साल
   • 2018 साल
5. गीथूब पर, मैं निम्नलिखित लिंक पर 2 शांत एसवीएम कार्यान्वयन को उजागर कर सकता हूं:
   
   • एक घरेलू डेवलपर से विधायक एल्गोरिदम
   • ML-से-स्क्रैच

निष्कर्ष:

आपका ध्यान के लिए बहुत बहुत धन्यवाद! मैं किसी भी टिप्पणी, प्रतिक्रिया और सुझावों के लिए आभारी रहूंगा।
आपको इस लेख का पूरा कोड मेरे गितुब पर मिलेगा।

चौरसाई कोनों पर सुझाव के लिए धन्यवाद योर्को । एलेक्सी सिज़िक के लिए धन्यवाद - एक भौतिकी और प्रौद्योगिकी विभाग जिसने आंशिक रूप से कोड में निवेश किया है।