दृश्य सूचना सिद्धांत (भाग 2)

सूचना सिद्धांत से अवधारणाओं के विज़ुअलाइज़ेशन के लिए समर्पित लॉन्ग्रिड के अनुवाद का दूसरा भाग। दूसरा भाग एन्ट्रापी, क्रॉस एन्ट्रॉपी, कुल्बैक-लिबलर विचलन, आपसी जानकारी और आंशिक बिट्स से संबंधित है। सभी अवधारणाओं को उत्कृष्ट दृश्य स्पष्टीकरण के साथ प्रदान किया गया है।

धारणा की पूर्णता के लिए, दूसरे भाग को पढ़ने से पहले, मेरा सुझाव है कि आप पहले से खुद को परिचित कर लें ।

एन्ट्रापी गणना

याद रखें कि एक संदेश की लागत लंबी है $$$एल$ के बराबर है $$$\ frac {1} {2 ^ L}$ । हम दिए गए राशि के लायक संदेश की लंबाई पाने के लिए इस मूल्य को उल्टा कर सकते हैं: $$$\ log_2 (\ frac {1} {लागत})$ । चूंकि हम खर्च करते हैं $$$p (x)$ प्रति कोडवर्ड के लिए $$$x$ , लंबाई बराबर होगी $$$\ log_2 (\ frac {1} {p (x)})$ । आकृति में, कोड शब्दों की सबसे अच्छी लंबाई का विकल्प।



हमने पहले चर्चा की कि एक मौलिक सीमा है कि किसी दिए गए प्रायिकता वितरण से घटनाओं को व्यक्त करने के लिए एक औसत संदेश कितना कम हो सकता है $$$पी$ । यह सीमा, सर्वश्रेष्ठ कोडिंग प्रणाली का उपयोग करते समय औसत संदेश लंबाई, एन्ट्रापी कहलाती है $$$पी, एच (पी)$ । अब जब हम इष्टतम कोडवर्ड लंबाई जानते हैं, तो हम इसकी गणना कर सकते हैं!

$$

$$H (p) = \ sum_xp (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

(अक्सर, एन्ट्रापी के रूप में लिखा जाता है $$$H (p) = - \ sum p (x) \ log_2 (p (x))$ समानता का उपयोग करना $$$\ log (1 / a) = - \ log (a)$ । यह मुझे लगता है कि पहला संस्करण अधिक सहज है, इसलिए हम इसका उपयोग करना जारी रखेंगे।)

अगर मैं रिपोर्ट करना चाहता हूं कि क्या घटना हुई है, तो कोई फर्क नहीं पड़ता कि मैं क्या करता हूं, औसतन मुझे इतने सारे बिट्स भेजने की आवश्यकता है।

किसी चीज़ को प्रसारित करने के लिए आवश्यक जानकारी की औसत मात्रा में संपीड़न के प्रत्यक्ष परिणाम हैं। लेकिन क्या अन्य कारण हैं कि हमें इसका ध्यान रखना चाहिए? हाँ! यह मेरी अनिश्चितता का वर्णन करता है, और जानकारी को निर्धारित करना संभव बनाता है।

अगर मुझे पता था कि क्या होगा, तो मुझे एक संदेश नहीं भेजना होगा! यदि दो चीजें हैं जो 50% संभावना के साथ हो सकती हैं, तो मुझे केवल 1 बिट भेजने की आवश्यकता है। लेकिन अगर 64 अलग-अलग घटनाएं हैं जो एक ही संभावना के साथ हो सकती हैं, तो मुझे 6 बिट्स भेजने होंगे। अधिक ध्यान केंद्रित करने की संभावना, अधिक अवसर मुझे लघु मध्यम संदेशों के साथ स्मार्ट कोड बनाने के लिए है। अधिक अस्पष्टता, मेरी पोस्ट जितनी लंबी होनी चाहिए।

परिणाम जितना अनिश्चित होता है, उतना ही मैं औसतन सीखता हूं जब वे मुझे बताते हैं कि क्या हुआ था।

क्रॉस एन्ट्रापी

ऑस्ट्रेलिया जाने से कुछ समय पहले, बॉब ने एलिस से शादी की, वह भी काल्पनिक। मेरे आश्चर्य के साथ-साथ मेरे सिर में अन्य पात्रों के आश्चर्य के लिए, ऐलिस एक कुत्ता प्रेमी नहीं था। वह एक बिल्ली प्रेमी था। इसके बावजूद, वे जानवरों के साथ उनके सामान्य जुनून और उनकी बहुत सीमित शब्दावली में एक आम भाषा खोजने में सक्षम थे।



ये दोनों एक ही शब्द का उपयोग करते हैं, केवल विभिन्न आवृत्तियों के साथ। बॉब हर समय कुत्तों के बारे में बात करता है, एलिस हर समय बिल्लियों के बारे में बात करता है।

ऐलिस ने पहले मुझे बॉब के कोड का उपयोग करके संदेश भेजे। दुर्भाग्य से, उसके पद आवश्यकता से अधिक लंबे थे। बॉब के कोड को उसकी संभावना वितरण के लिए अनुकूलित किया गया है। ऐलिस के पास एक अलग संभावना वितरण है, और कोड उसके लिए इष्टतम नहीं है। जब बॉब अपने कोड का उपयोग करता है तो कोडवर्ड की औसत लंबाई 1.75 बिट्स होती है; जब ऐलिस इसका उपयोग करता है, तो 2.25। यह और भी बुरा होगा यदि दोनों एक समान नहीं थे!

किसी अन्य वितरण के लिए इष्टतम कोड के साथ एक वितरण से औसत संदेश की लंबाई को क्रॉस-एन्ट्रॉपी कहा जाता है। औपचारिक रूप से, हम क्रॉस एन्ट्रॉपी को इस प्रकार परिभाषित कर सकते हैं:

$$

$$H_p (q) = \ sum_xq (x) \ log_2 \ Bigg (\ frac {1} {p (x)} \ Bigg)$$

इस मामले में, हम एलिस के कैटवॉर्म की शब्द आवृत्ति के क्रॉस-एन्ट्रोपी के बारे में बात कर रहे हैं, जो बॉब के कुत्ते प्रेमी की शब्द आवृत्ति के संबंध में है।



हमारे कनेक्शन की लागत को कम करने के लिए, मैंने ऐलिस को अपने स्वयं के कोड का उपयोग करने के लिए कहा। मेरी राहत के लिए, इसने अपनी औसत संदेश लंबाई कम कर दी। लेकिन इससे एक नई समस्या पैदा हो गई: कभी-कभी बॉब ने गलती से एलिस कोड का इस्तेमाल किया। हैरानी की बात यह है कि जब ऐलिस ने बॉब के कोड का उपयोग किया तो बॉब ने ऐलिस के कोड का उपयोग किया तो यह और भी बुरा था!

तो अब हमारे पास चार संभावनाएँ हैं:

• बॉब देशी कोड का उपयोग करता है ( $$$H (p) = 1.75$ बिट्स)
• ऐलिस बॉब के कोड का उपयोग करता है ( $$$H_p (q) = 2.25$ बिट्स)
• ऐलिस अपने कोड का उपयोग करता है ( $$$H (q) = 1.75$ बिट्स)
• बॉब ऐलिस कोड का उपयोग करता है ( $$$H_q (p) = 2.375$ बिट्स)

यह उतना सहज नहीं है जितना कोई सोच सकता है। उदाहरण के लिए, हम इसे देख सकते हैं $$$H_p (q) _ H_q (p)$ । क्या हम किसी तरह देख सकते हैं कि ये चार अर्थ एक दूसरे से कैसे संबंधित हैं?

निम्नलिखित चित्र में, प्रत्येक उपसमूह इन 4 संभावनाओं में से एक का प्रतिनिधित्व करता है। चित्र एक संदेश की औसत लंबाई की कल्पना करते हैं। उन्हें एक वर्ग में व्यवस्थित किया जाता है, ताकि यदि संदेश समान वितरण से हों, तो पास में चार्ट हों, और यदि वे समान कोड का उपयोग करते हैं, तो वे एक दूसरे के ऊपर होते हैं। यह आपको नेत्रहीन रूप से वितरण और कोड को एक साथ संयोजित करने की अनुमति देता है।



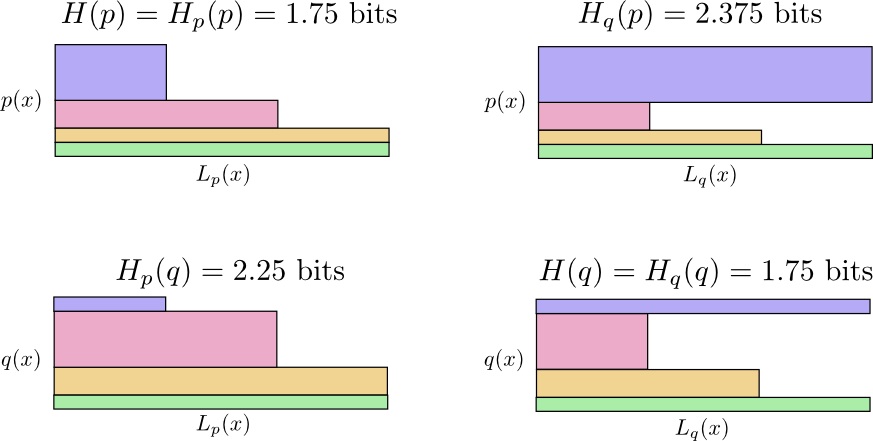
क्यों देखें $$$H_p (q) _ H_q (p)$ ? $$$H_q (p)$ इतना बड़ा, क्योंकि नीले रंग में चिह्नित घटना अक्सर होती है $$$पी$ लेकिन एक लंबा कोडवर्ड मिलता है क्योंकि यह बहुत दुर्लभ है $$$q$ । दूसरी ओर, लगातार घटनाओं के साथ $$$q$ के साथ कम आम है $$$पी$ लेकिन अंतर कम नाटकीय है, इसलिए $$$H_p (q) Hp (q)$ थोड़ा कम।

क्रॉस एन्ट्रापी सममित नहीं है।

तो आपको क्रॉस एन्ट्रॉपी की परवाह क्यों करनी चाहिए? क्रॉस एन्ट्रॉपी हमें यह व्यक्त करने का एक तरीका देता है कि दो संभावना वितरण कितने अलग हैं। जितना अधिक वितरण $$$पी$ और $$$q$ अधिक से अधिक क्रॉस एन्ट्रापी $$$पी$ के बारे में $$$q$ अधिक एन्ट्रापी होगी $$$पी$ ।



इसी तरह और $$$q$ से अलग है $$$पी$ अधिक से अधिक क्रॉस एन्ट्रापी $$$q$ के बारे में $$$पी$ अधिक एन्ट्रापी होगी $$$q$ ।

वास्तव में दिलचस्प बात एन्ट्रापी और क्रॉस एन्ट्रॉपी के बीच का अंतर है। यह अंतर हमारे पदों के कितने समय के बराबर है, क्योंकि हमने दूसरे वितरण के लिए अनुकूलित कोड का उपयोग किया है। यदि वितरण समान हैं, तो यह अंतर शून्य होगा। जैसे-जैसे अंतर बढ़ता जाएगा, यह बड़ा होता जाएगा।

हम इस अंतर को कुल्बैक-लीब्लर डाइवर्जेंस, या केएल डाइवरेज कहते हैं। केएल विचलन $$$पी$ के बारे में $$$q$ । $$$D_q (p)$ निम्नानुसार परिभाषित किया गया है:

$$

$$D_q (p) = H_q (p) - H (p)$$

केएल विचलन के बारे में महान बात यह है कि यह दो वितरणों के बीच की दूरी की तरह दिखता है। यह मापता है कि वे कितने अलग हैं! (यदि आप इस विचार को गंभीरता से लेते हैं, तो आप सूचना ज्यामिति पर आ जाएंगे।)

क्रॉस एन्ट्रापी और केएल डाइवरेजेशन मशीन लर्निंग में अविश्वसनीय रूप से उपयोगी हैं। अक्सर हम चाहते हैं कि एक वितरण दूसरे के करीब हो। उदाहरण के लिए, हम चाहते हैं कि अनुमानित वितरण अंतर्निहित सत्य के करीब हो। केएल विचलन हमें ऐसा करने का एक प्राकृतिक तरीका देता है, और इसलिए यह हर जगह खुद को प्रकट करता है।

एन्ट्रापी और कई चर

आइये पहले दिए गए हमारे मौसम और कपड़ों के उदाहरण पर वापस आते हैं:




मेरी मां, कई माता-पिता की तरह, कभी-कभी चिंता करती है कि मैं मौसम के लिए उचित रूप से पोशाक नहीं करता हूं। (उसे संदेह का अच्छा कारण है - मैं कभी-कभी सर्दियों में रेनकोट नहीं पहनता।) इसलिए, वह अक्सर मौसम जानना चाहता है और मैंने क्या पहना है। मुझे इसे रिपोर्ट करने के लिए कितने बिट्स भेजने चाहिए?

इसके बारे में सोचने का सबसे आसान तरीका संभावना वितरण भी है:



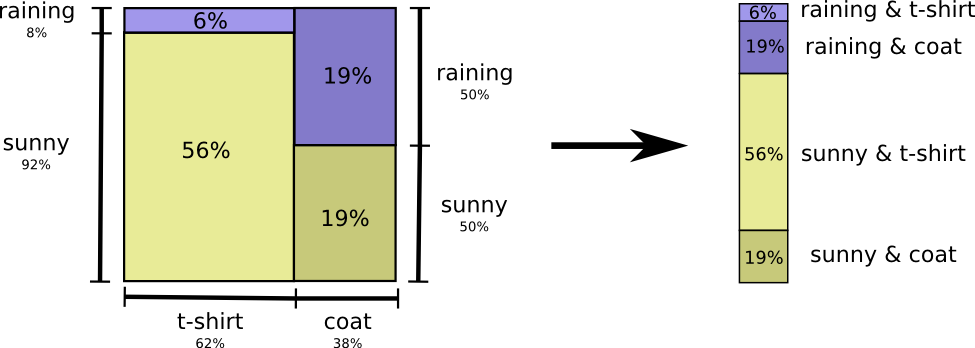
अब हम ऐसी संभावनाओं वाली घटनाओं के लिए इष्टतम कोड शब्दों की गणना कर सकते हैं और औसत संदेश लंबाई की गणना कर सकते हैं:



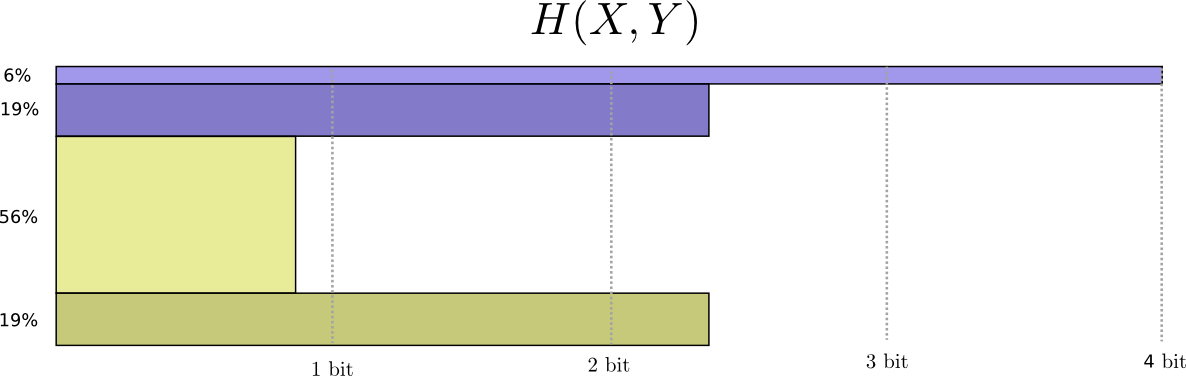
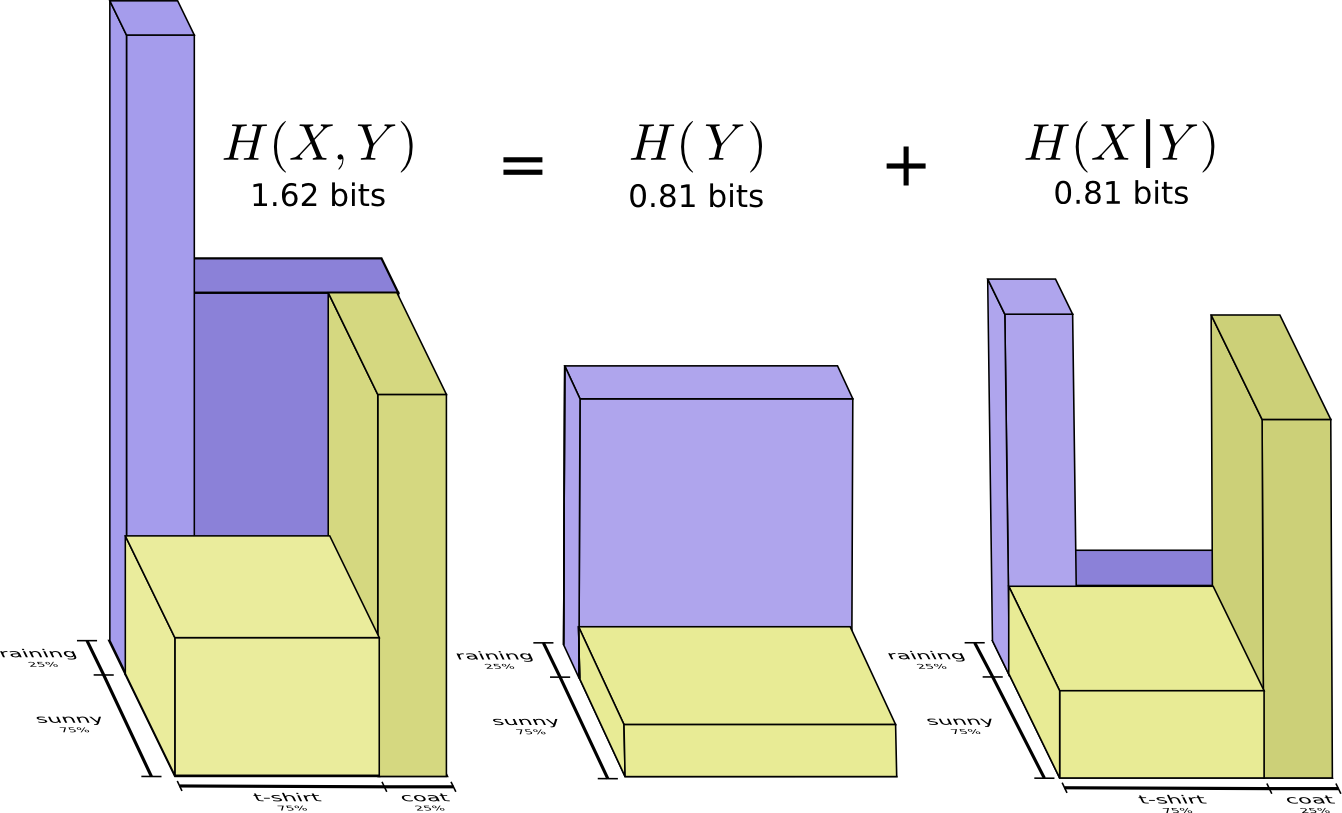
हम इसे संयुक्त एन्ट्रापी कहते हैं $$$X$ और $$$य$ निम्नानुसार परिभाषित किया गया है:

$$

$$H (X, Y) = \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x, y)} \ bigg)$$

यह हमारी सामान्य परिभाषा से मेल खाता है, एक के बजाय दो चर के अपवाद के साथ।

इसकी थोड़ी बेहतर छवि, वितरण को बराबर किए बिना, तीसरे आयाम में कोड शब्द की लंबाई का प्रतिनिधित्व करके प्राप्त की जाती है। अब एन्ट्रापी वॉल्यूम है!



लेकिन मान लीजिए मेरी मां को पहले से ही मौसम का पता है। वह उसे समाचार में देख सकता है। मुझे कितनी जानकारी प्रदान करने की आवश्यकता है?

लगता है कि मुझे यह बताने के लिए पर्याप्त जानकारी भेजने की आवश्यकता है कि मैंने क्या कपड़े पहने हैं। लेकिन वास्तव में, मुझे कम जानकारी भेजने की आवश्यकता है, क्योंकि मैं जो भी मौसम पहनता हूं वह मौसम पर बहुत निर्भर करता है! आइए बारिश और सूरज के मामले को अलग-अलग देखें।



दोनों मामलों में, मुझे औसत पर बहुत अधिक जानकारी भेजने की आवश्यकता नहीं है, क्योंकि मौसम मुझे एक अच्छा अनुमान देता है कि सही उत्तर क्या होगा। जब सूरज, मैं सूरज के लिए अनुकूलित एक विशेष कोड का उपयोग कर सकता हूं, और जब बारिश होती है, तो मैं बारिश के लिए अनुकूलित कोड का उपयोग कर सकता हूं। यदि मैं दोनों के लिए समान कोड का उपयोग करता हूं, तो दोनों मामलों में, मैं कम जानकारी भेजता हूं। मुझे अपनी माँ को भेजने के लिए औसत जानकारी प्राप्त करने के लिए, मैंने इन दोनों मामलों को एक साथ रखा है ...



हम इस सशर्त एन्ट्रापी को कहते हैं। यदि आप एक समीकरण में इसे औपचारिक रूप देते हैं, तो आपको यह मिलता है:

$$

$$H (X | Y) = \ sum_yp (y) \ sum_xp (x | y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg)$$

$$

$$= \ sum_ {x, y} p (x, y) \ log_2 \ bigg (\ frac {1} {p (x | y)} \ bigg) $$$

परस्पर जानकारी

पिछले अनुभाग में, हमें पता चला कि एक चर को जानने का मतलब यह हो सकता है कि दूसरे चर के मूल्य को संप्रेषित करने के लिए कम जानकारी की आवश्यकता है।

इसके बारे में सोचने का एक अच्छा तरीका धारियों के रूप में जानकारी की मात्रा की कल्पना करना है। यदि इन दोनों के बीच सामान्य जानकारी है तो ये बैंड ओवरलैप करते हैं। उदाहरण के लिए, जानकारी में से कुछ $$$X$ और $$$य$ इसलिए आम है $$$H (X)$ और $$$H (Y)$ अतिव्यापी धारियाँ हैं। और कब से $$$H (X, Y)$ दोनों चर की जानकारी है, तो यह संघों का संघ है $$$H (X)$ और $$$H (Y)$ ।



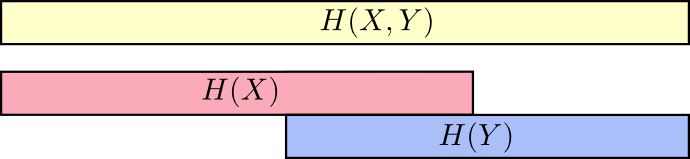
जब हम इस तरह से चीजों के बारे में सोचते हैं, तो बहुत कुछ देखना आसान हो जाता है।

उदाहरण के लिए, हमने पहले ही नोट कर लिया है कि जानकारी को किस रूप में प्रसारित करना है $$$X$ तो और $$$य$ ("संयुक्त एन्ट्रापी", $$$H (X, Y)$ ) अधिक जानकारी केवल ट्रांसमिशन के लिए आवश्यक है $$$X$ ("अंतिम एन्ट्रापी", $$$H (X)$ )। लेकिन अगर आप पहले से ही जानते हैं $$$य$ फिर प्रसारण के लिए $$$X$ ("सशर्त एन्ट्रापी", $$$H (X | Y)$ ) कम जानकारी की आवश्यकता है अगर आप यह नहीं जानते थे!



यह जटिल लगता है, लेकिन यदि आप बैंड में अनुवाद करते हैं तो सब कुछ बहुत सरल हो जाता है। $$$H (X | Y)$ क्या सूचना हमें सूचित करने के लिए भेजनी चाहिए $$$X$ जो पहले से ही जानता है $$$य$ में जानकारी $$$X$ जो अंदर भी नहीं है $$$य$ । नेत्रहीन, इसका मतलब है कि $$$H (X | Y)$ - यह पट्टी का हिस्सा है $$$H (X)$ जिसके साथ ओवरलैप नहीं होता है $$$H (Y)$ ।

अब आप असमानता को पढ़ सकते हैं $$$H (X, Y) (H (X) XH (X | Y)$ अगले चार्ट पर सही।



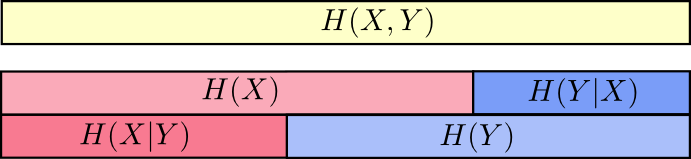
एक और समानता इस प्रकार है - $$$H (X, Y) = H (Y) + H (X | Y)$ । यानी में जानकारी $$$X$ और $$$य$ इसमें जानकारी है $$$य$ में प्लस जानकारी $$$X$ जो अंदर नहीं है $$$य$ ।



फिर, यह समीकरणों में देखना मुश्किल है, लेकिन यह देखना आसान है कि क्या आप सूचनाओं के अतिव्यापी बैंड के संदर्भ में सोचते हैं।

इस बिंदु पर, हमने जानकारी को तोड़ दिया $$$X$ और $$$य$ कई मायनों में। हम प्रत्येक चर में जानकारी जानते हैं, $$$H (X)$ और $$$H (Y)$ । हम दोनों में जानकारी के संयोजन को जानते हैं $$$H (X, Y)$ । हमारे पास ऐसी जानकारी है जो एक चर में है लेकिन दूसरे में नहीं है, $$$H (X | Y)$ और $$$H (Y | X)$ । इसमें से अधिकांश सूचना चर के लिए आम घूमती है - उनकी जानकारी का प्रतिच्छेदन। हम इसे "आपसी जानकारी" कहते हैं $$$I (x, y)$ के रूप में परिभाषित:

$$

$$I (X, Y) = H (X) + H (Y) XH (X, Y)$$

यह परिभाषा सत्य है क्योंकि $$$H (X) + H (Y)$ इसमें आपसी जानकारी की दो प्रतियां शामिल हैं, क्योंकि यह भी स्थित है $$$X$ और में $$$य$ , जबकि $$$H (X, Y)$ केवल एक प्रति शामिल है। (पिछले आरेख देखें)

सूचना का भिन्नता पारस्परिक जानकारी से निकटता से संबंधित है। सूचना का रूपांतर ऐसी जानकारी है जो चर के लिए सामान्य नहीं है। हम इसे इस तरह परिभाषित कर सकते हैं:

$$

$$V (X, Y) = H (X, Y) (I (X, Y)$$

सूचना का भिन्न होना इस मायने में दिलचस्प है कि यह हमें एक मीट्रिक देता है, विभिन्न चर के बीच की दूरी की अवधारणा। दो चर के बीच सूचना की भिन्नता शून्य होती है यदि एक चर का मूल्य आपको दूसरे का अर्थ बताता है और वे अधिक स्वतंत्र हो जाते हैं।

यह केएल विचलन से कैसे संबंधित है, जो हमें दूरी की अवधारणा भी देता है? केएल विचलन एक ही चर या चर के सेट पर दो वितरणों के बीच की दूरी है। इसके विपरीत, सूचना की भिन्नता हमें दो सह-वितरित चर के बीच की दूरी प्रदान करती है। केएल विचलन वितरण के बीच एक विसंगति है, एक वितरण के भीतर सूचना का एक रूपांतर।

हम इन सभी को विभिन्न प्रकार की सूचनाओं को जोड़ने वाले एकल आरेख में एक साथ ला सकते हैं:

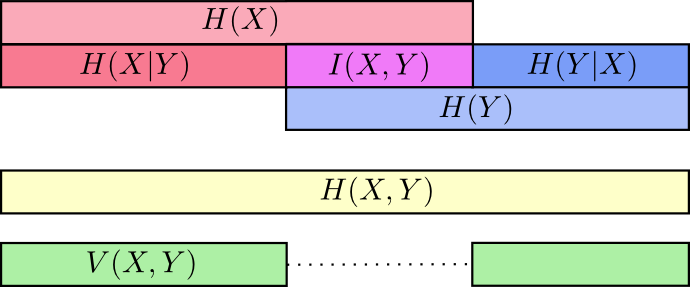
अंश बिट्स

सूचना सिद्धांत में एक बहुत ही अनपेक्षित बात यह है कि हमारे पास बिट्स की आंशिक संख्या हो सकती है। यह काफी अजीब है। आधा सा का क्या मतलब है?

यहां एक सरल उत्तर है: अक्सर हम किसी संदेश की औसत लंबाई में रुचि रखते हैं, बजाय किसी विशेष संदेश की लंबाई के। यदि आधे मामलों में एक बिट भेजा जाता है, और आधे मामलों में दो, तो औसतन डेढ़ बिट्स भेजे जाते हैं। इस तथ्य में कुछ भी अजीब नहीं है कि औसत आंशिक हो सकता है।

लेकिन इस जवाब से हम सवाल करने से कतराते हैं। अक्सर इष्टतम कोडवर्ड की लंबाई भी आंशिक होती है। इसका क्या मतलब है?

विशिष्ट होने के लिए, आइए संभावना वितरण को देखें, जहां एक घटना, $$$एक$ 71% समय होता है, और एक अन्य घटना, $$$ब$ 29% समय होता है।



इष्टतम कोड प्रतिनिधित्व करने के लिए 0.5 बिट का उपयोग करेगा $$$एक$ और 1.7 बिट्स का प्रतिनिधित्व करने के लिए $$$ब$ । ठीक है, अगर हम इनमें से केवल एक कोड शब्द भेजना चाहते हैं, तो ऐसा प्रतिनिधित्व असंभव है। हम बिट्स के पूर्णांक संख्या पर चक्कर लगाने के लिए मजबूर हैं और औसतन 1 बिट भेजते हैं।

... लेकिन अगर हम एक ही समय में कई संदेश भेजते हैं, तो यह पता चलता है कि हम बेहतर कर सकते हैं। आइए इस वितरण से दो घटनाओं के प्रसारण पर विचार करें। यदि हम उन्हें स्वतंत्र रूप से भेजते हैं, तो हमें दो बिट्स भेजने होंगे। हम इसे कैसे सुधारेंगे?



आधे मामलों में हमें भेजने की आवश्यकता है $$$आ$ 21% मामलों में - $$$अब$ या $$$बा$ , और 8% मामलों में - $$$bb$ । फिर से, एक आदर्श कोड में आंशिक बिट शामिल हैं।



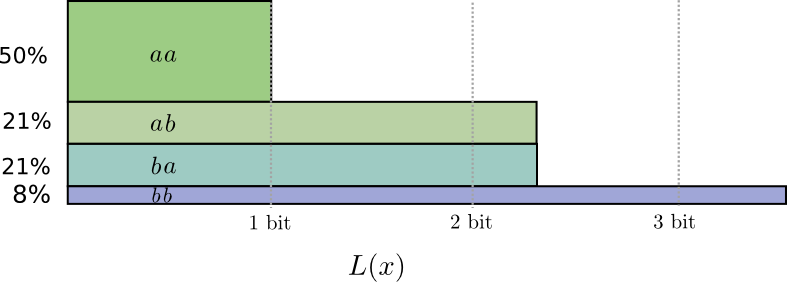
यदि हम कोडवर्ड की लंबाई को गोल करते हैं, तो हमें कुछ इस तरह मिलता है:



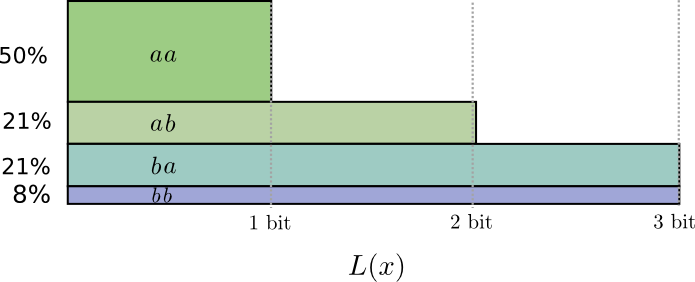
ये कोड हमें औसत संदेश लंबाई 1.8 बिट्स देते हैं। यह 2 बिट्स से कम है जब हम स्वतंत्र रूप से संदेश भेजते हैं। यानी इस स्थिति में, हम प्रत्येक घटना के लिए औसतन 0.9 बिट्स भेजते हैं। यदि हम एक बार में अधिक कार्यक्रम भेजते हैं, तो औसत भी कम होगा। पर $$$एन$ अनंत के लिए, हमारे कोड को गोल करने से जुड़े ओवरहेड गायब हो जाएंगे, और कोडवर्ड प्रति बिट्स की संख्या एन्ट्रापी में परिवर्तित हो जाएगी।

अगला, ध्यान दें कि घटना के लिए आदर्श कोडवर्ड लंबाई $$$एक$ 0.5 बिट था, और कोडवर्ड के लिए आदर्श लंबाई $$$आ$ - 1 बिट। आदर्श कोडवर्ड की लंबाई बढ़ जाती है, भले ही वे आंशिक हों! इसलिए, यदि हम एक साथ कई घटनाओं की रिपोर्ट करते हैं, तो लंबाई बढ़ जाएगी।

जैसा कि हम देख सकते हैं, जानकारी के बिट्स की आंशिक संख्या के लिए एक वास्तविक अर्थ है, भले ही वास्तविक कोड केवल पूर्णांक का उपयोग कर सकते हैं।

(व्यवहार में, लोग कुछ कोडिंग योजनाओं का उपयोग करते हैं जो विभिन्न मामलों में प्रभावी होती हैं। हफ़मैन कोड, जो वास्तव में एक प्रकार का कोड है जिसे हमने यहां स्केच किया है, आंशिक रूप से आंशिक रूप से बिट्स को हैंडल नहीं करता है - आपको वर्णों को समूह बनाना चाहिए जैसा कि ऊपर किया गया था, या उपयोग करें एन्ट्रापी की सीमा के करीब आने के लिए अधिक जटिल चालें। अंकगणित कोडिंग थोड़ा अलग है, यह सुरुचिपूर्ण ढंग से आंशिक रूप से इष्टतम होने के लिए आंशिक बिट्स को संसाधित करता है।)

निष्कर्ष

यदि हम बिट्स की न्यूनतम संख्या के लिए जानकारी के हस्तांतरण के बारे में चिंतित हैं, तो ये विचार निश्चित रूप से मौलिक हैं। यदि हम डेटा संपीड़न के बारे में परवाह करते हैं, तो सूचना सिद्धांत मुख्य मुद्दों को हल करता है और हमें मौलिक रूप से सही सार देता है। लेकिन अगर हम परवाह नहीं करते हैं - क्या वह विदेशी नहीं है?

सूचना सिद्धांत के विचार कई संदर्भों में दिखाई देते हैं: मशीन लर्निंग, क्वांटम भौतिकी, आनुवांशिकी, थर्मोडायनामिक्स, और यहां तक ​​कि जुआ भी। इन क्षेत्रों में चिकित्सकों को सूचना सिद्धांत की परवाह नहीं है क्योंकि वे जानकारी को संपीड़ित करना चाहते हैं। वे परवाह करते हैं कि इसका उनके क्षेत्र के साथ एक अनूठा संबंध है। क्वांटम उलझाव को एन्ट्रापी द्वारा वर्णित किया जा सकता है। सांख्यिकीय यांत्रिकी और ऊष्मप्रवैगिकी में कई परिणाम उन चीजों के बारे में अधिकतम एन्ट्रापी प्राप्त करके प्राप्त किए जा सकते हैं जिन्हें आप नहीं जानते हैं। खिलाड़ी लाभ और हानि सीधे केएल विचलन से संबंधित हैं, विशेष रूप से, पुनरावृत्त सेटअप।

इन सभी स्थानों पर सूचना सिद्धांत दिखाई देता है क्योंकि यह कई चीजों के लिए ठोस, मौलिक औपचारिकताएं प्रदान करता है जिन्हें हमें व्यक्त करना चाहिए। यह हमें अनिश्चितता को मापने और अभिव्यक्त करने के तरीके देता है, कि विश्वासों के दो सेट कितने अलग हैं, और यह कि एक प्रश्न का उत्तर हमें दूसरे के बारे में बताता है: कैसे फैलाव संभाव्यता है, संभाव्यता वितरण के बीच की दूरी, और दो चर कितने निर्भर हैं। क्या कोई विकल्प, समान विचार हैं? बेशक। लेकिन सूचना के सिद्धांत से विचार शुद्ध हैं, उनके पास वास्तव में अच्छे गुण हैं और सिद्धांतों पर आधारित हैं। कुछ मामलों में, ये विचार ठीक वही हैं जो आपको चाहिए, और अन्य मामलों में, वे एक अराजक दुनिया में एक सुविधाजनक मध्यस्थ हैं।

मशीन लर्निंग जो मुझे सबसे अच्छी तरह से पता है, तो चलिए एक मिनट के बारे में बात करते हैं। मशीन लर्निंग में एक बहुत ही सामान्य प्रकार का कार्य वर्गीकरण है। मान लीजिए हम एक तस्वीर को देखना चाहते हैं और भविष्यवाणी करते हैं कि क्या यह कुत्ते या बिल्ली की तस्वीर होगी। हमारा मॉडल कुछ ऐसा कह सकता है: "एक 80% संभावना है कि यह एक कुत्ते की तस्वीर है, और 20% संभावना है कि यह एक बिल्ली है।" मान लीजिए कि सही उत्तर एक कुत्ता है - हमने कितना अच्छा या बुरा कहा है। एक कुत्ता 80% क्या है? 85% कितना बेहतर कहेंगे?

यह एक महत्वपूर्ण प्रश्न है क्योंकि हमें सफलता के लिए इसे अनुकूलित करने के लिए हमारे मॉडल को कितना अच्छा या बुरा है, इस बारे में कुछ जानकारी चाहिए। हमें क्या अनुकूलन करना चाहिए? सही उत्तर वास्तव में इस बात पर निर्भर करता है कि हम किस मॉडल का उपयोग करते हैं: क्या हम केवल इस बात की परवाह करते हैं कि क्या हमारा अनुमान सही था, या हमें इस बात की परवाह है कि हम सही उत्तर में कितने आश्वस्त हैं?आत्मविश्वास से गलत होना कितना बुरा है? इसका कोई एक सही उत्तर नहीं है। और अक्सर सही उत्तर का पता लगाना असंभव होता है, क्योंकि हम यह नहीं जानते हैं कि मॉडल का उपयोग कैसे किया जाएगा जो आखिरकार हमें उत्साहित करता है। ऐसी स्थितियां हैं जब क्रॉस एन्ट्रॉपी बिल्कुल वही है जो हमें चिंतित करता है, लेकिन यह हमेशा ऐसा नहीं होता है। अधिक बार, हम नहीं जानते कि वास्तव में हमें क्या चिंता है, और क्रॉस-एन्ट्रॉपी वास्तव में अच्छा प्रॉक्सी है।

सूचना हमें दुनिया के बारे में सोचने के लिए एक मजबूत नया आधार देती है। कभी-कभी यह किसी दिए गए कार्य के लिए आदर्श होता है; अन्य मामलों में, काफी नहीं, लेकिन फिर भी बेहद उपयोगी है। इस निबंध ने केवल सूचना के सिद्धांत की सतह को खरोंच दिया - इसमें बुनियादी विषय हैं, जैसे त्रुटि सुधार कोड, जो हम बिल्कुल भी नहीं छूते थे, लेकिन मुझे आशा है कि मैंने दिखाया है कि सूचना सिद्धांत एक अद्भुत विषय है जिसे डराना नहीं चाहिए।