जीपीआर मॉडलिंग

जियोराडार (रेडियो-टेक्निकल डिवाइस ऑफ सबसर्फ़ साउंडिंग, जीपीआर, ग्राउंड पेनेट्रेटिंग रडार), जो वर्तमान में बहुत व्यापक रूप से उपयोग किया जाता है - खरगोश के छेदों की मैपिंग और छिपकलियों का अध्ययन करने से लेकर मेरी खोजों तक , एक महंगी कीमत है।


जीपीआर डिस्प्ले (ब्रिटिश टीवी शो "कमांड ऑफ़ द टाइम" से फ्रेम)

लेकिन इसकी क्षमताओं का मूल्यांकन करना और "आयरन" डिवाइस को प्राप्त / किराए पर लिए बिना पर्यावरण के साथ जियोराडार के विद्युत चुम्बकीय क्षेत्र की बातचीत के विभिन्न पहलुओं का अध्ययन करना संभव है। जीएनयू जीपीएल v3 लाइसेंस के तहत वितरित किए गए gprMax पैकेज ( जीपीआर - जीपीआर संक्षिप्त नाम से, मैक्स - जेम्स क्लर्क मैक्सवेल के नाम के शुरुआती अक्षर, जिन्होंने इलेक्ट्रोडायनामिक्स की नींव रखी)।
1996 में शुरू हुई इस परियोजना के लेखक , एडिनबर्ग विश्वविद्यालय के नॉर्थुम्ब्रिया विश्वविद्यालय के क्रेग वारेन और एंटोनीस गियानोपोलोस हैं। पैकेज मूल रूप से सी में विकसित किया गया था और फिर पायथन 3 / साइथन संयोजनों में पूरी तरह से फिर से लिखा गया था।


पैकेज स्थापित करने के लिए ओपनएमपी का समर्थन करने वाले स्थापित कंपाइलरों की आवश्यकता होती है (लिनक्स के लिए विंडोज विजुअल सी +१०११ बिल्ड टूल्स (यह संस्करण अनुशंसित है!) लिनक्स के लिए), न्यूपी लाइब्रेरी और साइथन कंपाइलर। GitHub पर रिपॉजिटरी से डाउनलोड करने और प्रोजेक्ट के सोर्स कोड को अनपैक करने के बाद, रूट फोल्डर पर जाएं और कमांड्स निष्पादित करें:

python setup.py build python setup.py install 

"त्वरित शुरुआत" के रूप में, हम एक सरल द्वि-आयामी उदाहरण का उपयोग करते हुए पैकेज के साथ काम करने पर विचार करते हैं - एक स्पंदित रडार (आवेग जीपीआर) के संचारण एंटीना टी, एक विद्युत चुम्बकीय पल्स का उत्सर्जन करता है, जिसमें से ऊर्जा सीधे एन्टी वेव (सीधा - तरंग) के रूप में प्राप्त एंटीना आर तक पहुंचती है, और कुछ प्रवेश करती है। रेत के माध्यम से, यह संवाहक सिलेंडर की सतह से परिलक्षित होता है और एक परावर्तित तरंग (RW - परावर्तित तरंग) के रूप में प्राप्त एंटीना तक पहुँचता है:


इनपुट फ़ाइल प्रारूप
प्रोजेक्ट के रूट फोल्डर में मॉडल फोल्डर बनाएं, जिसमें हम टेक्स्ट फाइल hello.in को रखते हैं जिसमें सिमुलेशन (कमांड के नीचे दिए गए कमांड्स प्रोजेक्ट के वर्तमान (तीसरे) वर्जन के लिए हैं) पर काम कर रहे हैं।

प्रत्येक टीम का फॉर्म है:

 #: _1 _2 _3 ... 

एक लाइन पर केवल एक कमांड लिखा जा सकता है, और कमांड वाले लाइन का पहला वर्ण # होना चाहिए।

कमेंट्स के साथ हो सकते हैं कमेंट्स:

 ## 

आदेशों का क्रम वस्तुओं के निर्माण के लिए आदेशों के लिए महत्वपूर्ण है - इस तरह के आदेशों को इनपुट फ़ाइल में दिखाई देने वाले क्रम में निष्पादित किया जाता है।

नाड़ी का आकार

एक भू-गर्भीय द्वारा उत्सर्जित एक विद्युत चुम्बकीय नाड़ी एक नैनोसेकंड के कुछ अंश तक रहता है, इसके अलावा, तीन नाड़ी आकार सबसे अधिक उपयोग किए जाते हैं:

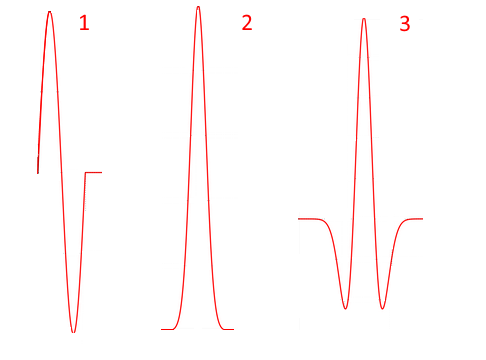
1. एक साइन लहर अवधि (साइन)
2. गाऊसी गति (गाऊसी)
3. मैक्सिकन टोपी (विकर) गाऊसी समारोह के दूसरे व्युत्पन्न के लिए आनुपातिक है, इस तरह के एक आवेग की वक्र आकृति एक सोमब्रेरो से मिलती है (यह आवेग रूप अमेरिकी भूभौतिकीय नॉर्मन रिकर द्वारा 1953 में भूकंपीय संकेतों का अध्ययन करने के लिए इस्तेमाल किया गया था)
   

हमारे उदाहरण के लिए, हम एक केंद्रीय आवृत्ति के साथ एक गाऊसी नाड़ी (पल्स प्रकार - गाऊसी) का चयन करते हैं $$$f_c = 1 \\ GHz = 1 \ cdot 10 ^ 9 हर्ट्ज$ कमांड द्वारा परिभाषित:

 #waveform: gaussian 1 1e9 pulse 

(1 - सशर्त नाड़ी आयाम, नाड़ी - नाड़ी लेबल)

इस स्थिति में, अनुकार में प्रयुक्त गति का वर्णन अभिव्यक्ति द्वारा किया गया है:

$$

$$W (t) = e ^ {- 2 \ cdot {\ pi} ^ 2 \ cdot {f_c} ^ 2 {(t- {1 \ over {f_c}}) ^ 2}$$

पर्यावरण मॉडल और समन्वय प्रणाली

2 डी मॉडलिंग में, अध्ययन किए गए क्षेत्र को दिए गए आकार की कोशिकाओं में विभाजित किया जाता है, और मॉडल समन्वय प्रणाली इस तरह दिखती है - एक्स और वाई कुल्हाड़ियों की गणना विमान (एक चौड़ाई के साथ) के रूप में होती है $$$w$ और लंबा $$$ज$ ), Z अक्ष के साथ मॉडल की लंबाई का नमूना चरण के बराबर मूल्य है $$$\ Delta$ ।


जब एक नमूना कदम चुनते हैं, तो आप अंगूठे के नियम का पालन कर सकते हैं - मॉडल में अध्ययन किए गए सबसे छोटे तरंग दैर्ध्य के दसवें आकार से अधिक नहीं होना चाहिए ("प्रति तरंग 10 कोशिकाएं"):

$$

$$\ Delta \ le 0,1 \ cdot {\ lambda} _ {min}$$

तरंग दैर्ध्य निर्धारित करने के लिए, किसी को उत्सर्जित सिग्नल के स्पेक्ट्रम में और खाते में विचार के तहत लहर के वेग में अधिकतम आवृत्ति को जानना होगा।

सापेक्ष ढांकता हुआ निरंतर के साथ एक माध्यम में एक विद्युत चुम्बकीय तरंग का प्रसार वेग $$${\ epsilon} _r$ , प्रति नैनोमीटर में सेंटीमीटर में व्यक्त किया जाता है - रडार में अपनाई गई गति की इकाई का निर्धारण अभिव्यक्ति द्वारा किया जाता है:

$$

$$v = {30 \ over {\ sqrt {{\ epsilon} _r}}}$$

सेंटीमीटर में तरंग दैर्ध्य अभिव्यक्ति द्वारा निर्धारित किया जाता है:

$$

$$\ lambda = {v \ over f}$$

( $$$च$ - GHz में आवृत्ति)।
गाऊसी नाड़ी और उसके स्पेक्ट्रम के आकार को प्रदर्शित करने के लिए, आप कमांड का उपयोग कर सकते हैं:

 python -m tools.plot_source_wave gaussian 1 1e9 5e-9 1e-12 -fft 

(गाऊसी - नाड़ी प्रकार, 1 - नाड़ी आयाम, 1e9 - केंद्र आवृत्ति (1 GHz), 5e-9 - नाड़ी प्रदर्शन अवधि (5 ns), 1e-12 - समय चरण (1 ps))


के साथ एक गाऊसी नाड़ी के स्पेक्ट्रम के अनुसार $$$f_s = 1 \ GHz$ निर्धारित करें कि -40 डीबी आवृत्ति पर $$$f \ लगभग 3 \ GHz$ ।
इस उदाहरण में, जिस माध्यम में प्रोब्ड ऑब्जेक्ट स्थित है, हम एक सापेक्ष परमिट के साथ सूखी रेत का चयन करते हैं $$${\ epsilon} _r = 3$ ।
रेत में विद्युत चुम्बकीय तरंग के प्रसार वेग का पता लगाएं:

$$

$$v = {30 \ over {\ sqrt {3}}} = 17.3 \ cm / ns$$

रेत में तरंग दैर्ध्य को परिभाषित करें:

$$

$$\ lambda = {v \ over f} = {17.3 \ over {3}} = 5.8 सेमी = 58 मिमी$$

इसके आधार पर, हम उस चरण का चयन करते हैं जो सभी अक्षों के लिए समान है ( $$$\ Delta = {\ Delta} _x = {\ Delta} _y = {\ Delta} _z$ ) और सुविधा के कारणों के लिए 2 मिमी = 0.002 मीटर के बराबर (चरणों का एक पूर्णांक 1 सेमी में फिट बैठता है):

 #dx_dy_dz: 0.002 0.002 0.002 

चौड़ाई को एक आयत तक सीमित करें $$$w$ 80 सेमी = 0.8 मीटर और ऊंचाई के बराबर $$$ज$ 60 सेमी = 0.6 मीटर के बराबर:

 #domain: 0.60 0.60 0.002 

(दो-आयामी मॉडल के लिए, एक कदम (0.002) के बराबर मोटाई का संकेत देना आवश्यक है)

सिमुलेशन क्षेत्र का आकार और स्थानिक चरण का आकार मॉडल कोशिकाओं की संख्या निर्धारित करता है और, तदनुसार, कंप्यूटर मेमोरी आवश्यकताओं।

हम विशिष्ट चालकता के साथ रेत का वर्णन करते हैं $$$\ _ सिग्मा = 0.01 \ \ सेमी / मी$ और सापेक्ष ढांकता हुआ निरंतर $$${\ epsilon} _r = 3$ आदेश:

 #material: 3 0.01 1 0 sand 

(1 सापेक्ष चुंबकीय पारगम्यता से मेल खाती है $$${\ _मु} _r$ एकता के बराबर (कोई चुंबकीय गुण नहीं), 0 - कोई चुंबकीय नुकसान नहीं, और रेत - इस सामग्री का लेबल)।

अधिकांश सिम्युलेटेड क्षेत्र के साथ रेत भरें (y = 0 से y = 38 सेमी = 0.38 मीटर):

 #box: 0 0 0 0.80 0.38 0.002 sand 

(0 0 0 - निचले बाएं कोने के निर्देशांक, 0.80 0.38 0.002 - ऊपरी दाएं कोने के निर्देशांक (0.002 - नमूना चरण))
शेष नि: शुल्क स्थान है (लेबल free_space), वायु गुणों में लगभग बराबर है ( $$${\ epsilon} _r = 1$ । $$${\ _मु} _r = 1$ । $$${\ _ सिग्मा} = 0$ )।
सिमुलेशन क्षेत्र की सीमाओं को अवशोषण सीमा स्थिति (एबीसी) के रूप में प्रस्तुत किया जाता है।

लक्ष्य के रूप में, हम एक आदर्श कंडक्टर (पूरी तरह से विद्युत चुम्बकीय विकिरण को दर्शाते हुए) से 6 सेमी = 0.06 मीटर की दूरी के साथ एक केंद्र चुनते हैं, जो निर्देशांक x = 25 सेमी = 0.25 मीटर और y = 10 सेमी / 0.1 मीटर के साथ एक बिंदु पर स्थित केंद्र के साथ है:

 #cylinder: 0.250 0.1 0 0.250 0.1 0.002 0.06 pec 

(पीईसी एक पूरी तरह से प्रवाहकीय सामग्री है)

एंटेना

सिम्युलेटेड जीपीआर दो एंटेना से सुसज्जित है - संचारण और प्राप्त करना।
हमारे मामले के अध्ययन में, हम एक हर्ट्ज डिपोल के साथ एक ट्रांसमिटिंग एंटीना का प्रतिनिधित्व करते हैं, जिसकी लंबाई नमूना चरण (तीन आयामी मामले में, आप एक व्यापक पुस्तकालय से एक ऐन्टेना का चयन कर सकते हैं) रेत के नीचे (प्रोम माध्यम के साथ संपर्क में) क्षेत्र के मध्य से 5 सेमी की दूरी पर (x = 35 =) सेमी = 0.35 मीटर, y = 38 सेमी = 0.38 मीटर):

 #hertzian_dipole: z 0.35 0.380 0.0 pulse 

(z द्विध्रुवीय ध्रुवीकरण अक्ष है (द्वि-आयामी मामले (2D TMz मोड के लिए) केवल z वैध है), पल्स ऐन्टेना द्वारा निकाली गई नाड़ी के आकार का लेबल है)

प्राप्त करने वाला एंटीना आमतौर पर प्राप्त करने से थोड़ी दूरी पर स्थित होता है, जिसे एंटीना इकाई का आधार कहा जाता है (एंटेना की सापेक्ष स्थिति के लिए यह विकल्प "सामान्य-ऑफसेट" कहा जाता है)। आधार के रूप में, 10 सेमी की दूरी का चयन करें, इसलिए क्षैतिज समन्वय 35 + 10 = 45 सेमी = 0.45 मीटर (क्षेत्र के मध्य के दाईं ओर 5 सेमी):

 #rx: 0.45 0.38 0.0 

सिमुलेशन अंतराल

मॉडलिंग के लिए समय खिड़की का विकल्प निर्धारित किया जाता है ताकि लक्ष्य से परिलक्षित संकेत प्राप्त एंटीना तक पहुंचने का समय हो।

हम विचार के तहत मामले में संकेत द्वारा आवश्यक अनुमानित समय निर्धारित करते हैं, एंटेना से लक्ष्य तक दूरी ले जाते हैं $$$h = 18 \ \ cm$ :
$$$t \ लगभग {2 \ cdot h \ over {v}} = {2 \ cdot 18 \ over 17.3} = 2.1 \ \ n $$
यह देखते हुए कि 1 GHz की केंद्रीय आवृत्ति के साथ रडार की गाऊसी नाड़ी के शीर्ष को 1 ns द्वारा समय अक्ष की शुरुआत के सापेक्ष स्थानांतरित किया जाता है, हम 5 नैनोसेकंड की एक समय खिड़की का चयन करते हैं:

 #time_window: 5e-9 

मोडलिंग

इस प्रकार, इनपुट फ़ाइल की सामग्री इस प्रकार है:


हम मॉडलिंग की प्रक्रिया शुरू करते हैं:

 python -m gprMax models\hello.in 

सिमुलेशन करने के लिए, परिमित-अंतर समय-डोमेन विधि (FDTD, परिमित-अंतर-समय-डोमेन) का उपयोग किया जाता है (विधि का मूल एल्गोरिथ्म केन यी द्वारा प्रस्तावित किया गया था), जिसके बाद जिन कोशिकाओं में मॉडल विभाजित होता है, उन्हें रुपया कोशिकाएं कहा जाता है। । प्रत्येक सेल के लिए मैक्सवेल समीकरणों को हल करके समय डोमेन में एक संख्यात्मक समाधान प्राप्त किया जाता है।

द्वि-आयामी मामले में (2 डी TMz मोड), केवल घटक की गणना की जाती है $$$E_z$ बिजली के क्षेत्र और घटकों $$$H_x$ और $$$H_y$ चुंबकीय क्षेत्र।

यदि उपलब्ध मेमोरी की मात्रा पार हो गई है, तो अनुकरण करने के लिए मेमोरी की कमी के बारे में संदेश जारी किया जाता है:


यदि कोई भी ऑब्जेक्ट सिमुलेशन के दायरे से बाहर है, तो एक त्रुटि संदेश प्रदर्शित होता है:


वर्णित मॉडल के साथ अनुकरण करने के लिए, इसमें केवल 56 एमबी रैम लिया गया था (यदि आप चरण को आधा तक घटाते हैं - 1 मिमी तक - स्मृति आवश्यकताओं में 99 एमबी तक वृद्धि होती है)।

सिमुलेशन पूरा होने के बाद, हेलो.आउट फ़ाइल मॉडल फ़ोल्डर में दिखाई देती है, जिसमें सिमुलेशन परिणाम एचडीएफ 5 प्रारूप में होते हैं , विशेष रूप से संख्यात्मक डेटा संग्रहीत करने के लिए डिज़ाइन किया गया है।

ट्रैक बिल्डिंग

परिणामों की कल्पना करने के लिए, हम निशानों का निर्माण करते हैं:

 python -m tools.plot_Ascan models\hello.out 

प्रत्येक ट्रैक (ए-स्कैन) खिड़की में प्रस्तुत किया जाता है जो प्राप्त ऐन्टेना के स्थान पर विद्युत चुम्बकीय क्षेत्र के घटकों में से एक का समय रेखांकन प्रदर्शित करता है:


संचारण एंटीना (डीडब्ल्यू) से सीधे आने वाली एक सीधी लहर और लक्ष्य (आरडब्ल्यू) से परावर्तित एक लहर रास्तों पर दिखाई देती है।

समय की क्षैतिज अक्ष पदार्थ में विद्युत चुम्बकीय तरंग की गति के माध्यम से संकेत को दर्शाने वाले लक्ष्य की गहराई से संबंधित है।

लेकिन क्या होता है यदि आप इनपुट फ़ाइल में बॉक्स कमांड के सामने सिलेंडर कमांड डालते हैं?


सिलेंडर से परावर्तित सिग्नल गायब हो गया - रेत ने सिलेंडर को अवशोषित कर लिया (यह उस क्रम के महत्व का एक उदाहरण है जिसमें वस्तुओं का निर्माण होता है)।

प्रोफाइल बिल्डिंग

लेकिन अधिक जानकारीपूर्ण है राडारग्राम (रडारग्राम) - प्रोफाइल (बी-स्कैन), जो एक दिए गए दिशा के साथ जियोराडार को स्थानांतरित करते समय निर्मित कई पटरियों का एक संयोजन है - यह अध्ययनित क्षेत्र के साथ एक ट्रॉली के साथ एक ट्रॉली को स्थानांतरित करने के लिए बहुत ही प्रक्रिया है।

एंटेना के विवरण को क्षैतिज अक्ष की शुरुआत में ले जाकर बदलें:

 #hertzian_dipole: z 0.10 0.38 0.0 pulse #rx: 0.20 0.38 0.0 

हमने एंटेना को 1 सेमी = 0.01 मीटर के बराबर ले जाने के लिए चरण निर्धारित किया है:

 #src_steps: 0.01 0 0 #rx_steps: 0.01 0 0 

इस प्रकार, इनपुट फ़ाइल की सामग्री इस प्रकार है:


सिमुलेशन को बैच मोड में चलाएं:

 python -m gprMax models\hello.in -n 50 

(50 राडार कदम की संख्या है)।

शुरू करने के बाद, सिमुलेशन क्रमिक रूप से 50 जीपीआर पदों के लिए किया जाता है:


सिमुलेशन के अंत के बाद, मॉडल फ़ोल्डर में 50 फाइलें hello1.out ... hello50.out हैं।
इन फ़ाइलों को कमांड के साथ hello_merged.out फ़ाइल में मिलाएँ:

 python -m tools.outputfiles_merge models/hello 

एक प्रोफ़ाइल बनाएँ:

 python -m tools.plot_Bscan models\hello_merged.out Ez 

(ईज़ विद्युत चुम्बकीय क्षेत्र का वह घटक है जिसके द्वारा हम प्रोफ़ाइल बनाते हैं - वह घटक जो सीधे वोल्टेज में परिवर्तित हो जाता है)


जैसा कि आप देख सकते हैं, सीधी लहर के कारण क्षैतिज पट्टी ऊपर प्रोफ़ाइल पर प्रदर्शित होती है, और परावर्तित लहर के कारण होने वाली विशेषता हाइपरबोला और जब यह चलती है तो लक्ष्य से जीपीआर तक की दूरी को नीचे दिखाए जाने पर दिखाई देता है।

दाईं ओर की किंवदंती मिलान रंग और क्षेत्र की ताकत दिखाती है। $$$E_z$ (ट्रैक पर दिखाया गया है):
लाल - $$$E_z> 0$
सफेद - $$$E_z = 0$
नीला - $$$E_z <0$
इस तरह के प्रोफाइल का विश्लेषण करके, हम गहराई, आकार और यहां तक ​​कि लक्ष्यों के आकार के बारे में निष्कर्ष निकाल सकते हैं, और तंत्रिका नेटवर्क का उपयोग इसके लिए भी किया जाता है।


जीपीआर डिस्प्ले पर रूट और प्रोफाइल (ब्रिटिश टीवी शो "टाइम का कमांड")

लेकिन प्रतिबिंब न केवल प्रवाहकीय वस्तुओं से होता है, बल्कि विभिन्न ढांकता हुआ स्थिरांक के साथ दो परतों की सीमा पर भी होता है।

मॉडल के निचले हिस्से में ढांकता हुआ स्थिर के साथ एक दूसरी रेत परत बनाएं $$${\ epsilon} _r = 9$ :



जैसा कि देखा जा सकता है, प्रत्यक्ष लहर (डीडब्ल्यू) के "ट्रेस" के नीचे, दो रेत परतों के इंटरफ़ेस से परिलक्षित लहर (आरडब्ल्यू) का एक रैखिक खंड दिखाई दिया।

इस उदाहरण के दायरे के बाहर, gprMax विशेषताएं जैसे त्रि-आयामी मॉडलिंग, जटिल सतह आकार, विस्तृत एंटीना मॉडल, विद्युत चुम्बकीय तरंगों के फैलाव के लिए लेखांकन ... इसके अलावा, पैकेज का उपयोग न केवल जीपीआर का अनुकरण करने के लिए किया जा सकता है, बल्कि विभिन्न वातावरणों में विद्युत चुम्बकीय तरंगों के प्रसार का अध्ययन करने के लिए भी किया जा सकता है, और NVIDIA CUDA तकनीक का उपयोग करके गणना में तेजी लाएं , जो ओपनएमपी का उपयोग करके सीपीयू पर समानांतर कंप्यूटिंग की तुलना में गति में दस गुना वृद्धि प्रदान करता है। मॉडलिंग के लचीलेपन को बढ़ाने के लिए, आप इनपुट फ़ाइल में पायथन में कोड के ब्लॉक रख सकते हैं।

GprMax पैकेज का उपयोग करने के कुछ उदाहरण:

• एंटी-कर्मियों खानों की खोज में जीपीआर की प्रभावशीलता पर मिट्टी के गुणों के प्रभाव का आकलन
• मकई के बीज बोने की गहराई के गैर-विनाशकारी निर्धारण के लिए जमीन मर्मज्ञ रडार का उपयोग करने की संभावना की जांच करना
• राजमार्ग के माध्यम से भूमिगत मार्ग की संरचनाओं की ताकत के अध्ययन में जीपीआर क्षेत्र डेटा की व्याख्या की गुणवत्ता में सुधार
• परिलक्षित संकेत के आयाम और कंक्रीट में मजबूत सलाखों के व्यास के बीच संबंधों का अध्ययन
• पेड़ की चड्डी में voids का पता लगाने के लिए जीपीआर की उपयुक्तता का आकलन

उपयोगी लिंक:

gprMax आधिकारिक साइट
GprMax उपयोगकर्ता पुस्तिका
YouTube पर gprMax