पूरे भूगोल में: विभिन्न भाषाओं में नेविगेशन और भूगर्भीय कार्य

प्रणाम, प्यारे!

"जहाज का असली स्थान, हालांकि अज्ञात, आकस्मिक नहीं है, यह है, लेकिन यह किस बिंदु पर अज्ञात है" वी। अलेक्सिशिन एट अल। प्रैक्टिकल नेविगेशन, 2006। पी। 71

"पैदल यात्री आकाशगंगा के दो किनारों से बाहर आए ..." (सी) सर्गेई पोपोव (एस्ट्रोफिजिसिस्ट)

आर्ट नोव्यू शैली में नए रुझानों के प्रकाश में , मैं समतल जमीन पर भूगर्भिक समस्याओं को हल करने के बारे में लिखना चाहता था। लेकिन अब तक, यह कथन कि पृथ्वी के आकार को आसानी से एक दीर्घवृत्ताकार द्वारा अनुमानित किया गया है, विधर्म और राजद्रोह नहीं है, मैं सभी रूचि को अधिक रूढ़िवादी मॉडल में शामिल होने के लिए आमंत्रित करता हूं।

• दो भौगोलिक बिंदुओं के बीच की दूरी
• ज्ञात द्वारा एक बिंदु का निर्धारण, उससे दूरी और अज़ीमुथल कोण
• ज्ञात बिंदुओं के लिए मापा दूरी (TOA, TOF) द्वारा एक बिंदु की स्थिति का निर्धारण
• मापा संकेत आगमन समय (TDOA) द्वारा एक बिंदु की स्थिति का निर्धारण

यह सब C #, Rust और Matlab में, गोलाकार और दीर्घवृत्त पर, चित्र, ग्राफ़, स्रोत कोड - कट के नीचे।

और यह, प्रासंगिक केडीपीवी:



जल्दी में उन लोगों के लिए (मैं खुद हूं), यहां GitHub पर भंडार है , जहां परीक्षण और उदाहरण के साथ सभी स्रोत कोड हैं।

रिपॉजिटरी का आयोजन बहुत सरलता से किया जाता है: पुस्तकालय को वर्तमान में तीन भाषाओं में प्रस्तुत किया जाता है और प्रत्येक कार्यान्वयन अपने स्वयं के फ़ोल्डर में होता है:

• C #
• रतुआ
• मैटलैब

C # में सबसे पूर्ण कार्यान्वयन: दूसरों के विपरीत, इसमें तथाकथित तरीके हैं वर्चुअल लॉन्ग बेस - यह तब होता है जब एक ऑब्जेक्ट जिसकी स्थिति आपको निर्धारित करने की आवश्यकता होती है, स्थिर है, और एक ज्ञात स्थिति के साथ, विभिन्न बिंदुओं से इसे मापा जाता है।

यह देखने के लिए कि सब कुछ कैसे काम करता है, किन मापदंडों के साथ यह कॉल करता है और क्या रिटर्न देता है, और लड़ाई में टोही आचरण करता है, अलग-अलग डेमो और परीक्षण हैं:

• C # में टेस्ट कंसोल एप्लिकेशन
• मतलाब पर पूरे पुस्तकालय का परीक्षण करें
• TOA / TDOA डेमो स्क्रिप्ट मतलाब पर सुंदर चित्रों के साथ
• मैटलैब पर गोले की समस्याओं की सटीकता की तुलना करने के लिए मैटलैब पर एक क्षेत्र (हेवेरसाइन समीकरण) और एक दीर्घवृत्त (विन्सेन्टी समीकरण) पर
• रस्ट पर कार्यान्वयन के लिए, लाइब्रेरी कोड में परीक्षण शामिल हैं। और आप देख सकते हैं कि "कार्गो -टेस्ट" कमांड चलाकर सब कुछ कैसे काम करता है

मैंने पुस्तकालय को यथासंभव स्वतंत्र और आत्मनिर्भर बनाने की कोशिश की। ताकि अगर आप चाहें, तो आप केवल वांछित टुकड़ा ले सकते हैं (स्रोत का उल्लेख करते हुए, निश्चित रूप से), बाकी सब कुछ खींचे बिना।

लगभग हमेशा कोण रेडियन में होते हैं, मीटर में दूरी, सेकंड में समय।

अब, शुरू से शुरू करते हैं:

सर्वेक्षण कार्य

दो विशिष्ट भौगोलिक कार्य हैं: प्रत्यक्ष और व्युत्क्रम।

यदि उदाहरण के लिए, मैं अपने वर्तमान निर्देशांक (अक्षांश और देशांतर) को जानता हूं, और फिर मैं 1000 किलोमीटर तक उत्तर पूर्व, कुएं या उत्तर की ओर सख्ती से चला। अब मेरे पास क्या निर्देशांक होंगे? - एक प्रत्यक्ष जियोडेसिक समस्या को हल करने के लिए मेरे पास क्या निर्देशांक हैं, यह जानने के लिए।

वह है: एक प्रत्यक्ष जियोडेसिक कार्य एक ज्ञात दूरी और एक दिशा कोण द्वारा एक बिंदु के निर्देशांक का पता लगा रहा है।

उलटा समस्या के साथ, सब कुछ पूरी तरह से स्पष्ट है - उदाहरण के लिए, मैंने अपने निर्देशांक निर्धारित किए, और फिर मैं कुछ समय के लिए एक सीधी रेखा में चला गया और फिर से अपने निर्देशांक निर्धारित किए। मैं कितना गया इसका अर्थ है कि उलटे जियोडेसिक समस्या को हल करना।

वह यह है: व्युत्क्रम जियोडेसिक समस्या ज्ञात भौगोलिक निर्देशांक वाले दो बिंदुओं के बीच की दूरी का पता लगा रही है।

आप इन समस्याओं को कई तरीकों से हल कर सकते हैं, जो आवश्यक सटीकता और उस पर खर्च करने के लिए तैयार समय पर निर्भर करता है।

सबसे आसान तरीका यह कल्पना करना है कि पृथ्वी समतल है - यह एक गोला है। चलो इसे आजमाएँ।
यहाँ प्रत्यक्ष समस्या को हल करने का सूत्र है ( स्रोत ):

$$

$$\ phi_2 = आर्क्सिन (पाप \ phi_1cos \ delta + cos \ phi_1sin \ delta cos \ theta)$$

$$

$$\ lambda_2 = \ lambda_1 + atan2 (sin \ theta sin \ delta cos \ phi_1, cos \ delta-sin \ phi_1sin \ phi_2)$$

यहां $$$\ phi_1$। $$$\ lambda_1$- शुरुआती बिंदु का अक्षांश और देशांतर, $$$$ थीटा$- दिशात्मक कोण, उत्तर दिशा से घड़ी की दिशा में मापा जाता है (जब ऊपर से देखा जाता है), $$$\ डेल्टा$- कोणीय दूरी d / R। d मापा (यात्रा की गई) दूरी है, और R पृथ्वी की त्रिज्या है। $$$\ phi_2$। $$$\ lambda_2$- इच्छित बिंदु का अक्षांश और देशांतर (हम जो आए थे)।

उलटा समस्या को हल करने के लिए, एक और (कोई कम सरल सूत्र) नहीं है:

$$

$$a = sin ^ 2 (\ Delta \ phi / 2) + cos \ phi_1 cos \ phi_2 sin ^ 2 (\ Delta \ lambda / 2)$$

$$

$$d = R * atan2 (\ sqrt a, \ sqrt {1-a})$$

जहाँ $$$\ phi_1$। $$$\ lambda_1$और $$$\ phi_2$। $$$\ lambda_2$- बिंदुओं के निर्देशांक, आर - पृथ्वी त्रिज्या।

वर्णित सूत्रों को हावरसाइन समीकरण कहा जाता है।

• एक C # कार्यान्वयन में, संबंधित कार्यों को हैवेर्सडायरेक्ट और हैवेर्सइनइनवर्स कहा जाता है और अल्गोरिद्म में रहते हैं।
• जंग कार्यान्वयन में, ये haversine_direct और haversine_inverse फ़ंक्शन हैं ।
• अंत में, Matlab पर, फ़ंक्शंस को अलग-अलग फ़ाइलों में संग्रहीत किया जाता है, और यहाँ दोनों कार्य हैं:
  हैवरसाइनडायरेक्ट और हैवरसाइनइनवर्स

C # के लिए, मैं फ़ंक्शंस के नाम और फ़ाइल का लिंक प्रदान करूँगा जहाँ वे स्थित हैं। रस्ट के लिए - केवल फ़ंक्शन के नाम (चूंकि पूरी लाइब्रेरी एक फ़ाइल में है), और मतलाब के लिए - संबंधित स्क्रिप्ट फ़ाइल का लिंक, क्योंकि मैटलैब में एक फ़ंक्शन - एक स्क्रिप्ट है।

जाहिर है, किसी प्रकार की पकड़ है: पृथ्वी एक क्षेत्र नहीं है, लेकिन एक विमान है, और यह किसी भी तरह से इन सूत्रों और / या समाधान की सटीकता की प्रयोज्यता को प्रभावित करना चाहिए।

और वास्तव में। लेकिन इसे निर्धारित करने के लिए, आपको कुछ के साथ तुलना करने की आवश्यकता है।
1975 में वापस, थेडियस विंसेंटी ने एक गोलाकार की सतह पर प्रत्यक्ष और उलटे भू-समकालिक समस्याओं का एक कम्प्यूटेशनल रूप से कुशल समाधान प्रकाशित किया ( इसे क्रांति के एलीपोसिड के रूप में जाना जाता है , कॉमरेड! रोटेशन का एलिसॉइड, जो लगभग मानक हो गया है।

विधि डिवाइस का विवरण एक अलग लेख के लिए तैयार किया गया है, इसलिए मैं खुद को केवल विन्सेंटी के मूल काम में भेजने और एल्गोरिथ्म के विवरण के साथ एक ऑनलाइन कैलकुलेटर तक सीमित कर दूंगा।

UCNLNav पुस्तकालय में, विन्सेन्टी फ़ार्मुलों का उपयोग करके प्रत्यक्ष और विलोम जियोडेसिक समस्याओं का समाधान निम्नलिखित कार्यों में निहित है:

• एल्गोरिथम में C #: VincentyDirect और VincentyInverse ।
• जंग: vincenty_inverse और vincenty_direct
• मतलाब : Nav_vincenty_direct और Nav_vincenty_inverse ।

क्योंकि विन्सेन्टी का समाधान पुनरावृत्त है, फिर अधिकतम पुनरावृत्तियों (it_limit) पैरामीटर सूची में मौजूद हैं, और पुनरावृत्तियों की वास्तविक संख्या परिणाम सूची में है। स्टॉप कंडीशन (एप्सिलॉन) को निर्दिष्ट करने वाली एक दहलीज भी है। ज्यादातर मामलों में, 10 से अधिक पुनरावृत्तियों की आवश्यकता नहीं होती है, लेकिन लगभग एंटीपोडल बिंदु (जैसे कि उत्तर और दक्षिण ध्रुव) के लिए विधि खराब रूप से परिवर्तित होती है, और 2000 पुनरावृत्तियों तक की आवश्यकता हो सकती है।

सबसे महत्वपूर्ण अंतर यह है कि ये सूत्र एक गोलाकार पर समाधान को निष्पादित करते हैं, और इसके मापदंडों को कार्यों में स्थानांतरित किया जाना चाहिए। इसके लिए एक सरल संरचना है जो इसका वर्णन करती है।

सभी कार्यान्वयन में, मानक दीर्घवृत्त में से एक को एक पंक्ति में प्राप्त किया जा सकता है। (बहुत बार, WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] का उपयोग किया जाता है और हम इसे एक उदाहरण के रूप में देंगे:

• C # में: Algorithms.cs में एक स्थिर फ़ील्ड है Algorithms.WGS84Ellipsoid - इसे विधियों में पारित किया जा सकता है।
• जंग पर:

  let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); 

• मतलाब पर:

   el = Nav_build_standard_ellipsoid('WGS84'); 

शेष मापदंडों का नाम काफी स्पष्ट है और इसमें अस्पष्टता नहीं होनी चाहिए।

यह समझने के लिए कि एक दीर्घवृत्त के बजाय एक गोले के लिए समाधान का उपयोग करने के लिए हमें क्या लागत आएगी, मैटलैब कार्यान्वयन पर एक स्क्रिप्ट है।

मतलाब में, अनावश्यक इशारों के बिना कुछ भी प्रदर्शित करना सुविधाजनक है, इसलिए मैंने इसे प्रदर्शन के लिए चुना।

उनकी स्क्रिप्ट का तर्क:

1. हम मनमाने समन्वय के साथ एक बिंदु लेते हैं

 sp_lat_rad = degtorad(48.527683); sp_lon_rad = degtorad(44.558815); 

और एक मनमाना दिशा (मैंने पश्चिम के बारे में चुना):

 fwd_az_rad = 1.5 * pi + (rand * pi / 4 - pi / 8); 

2. हम इससे लगातार बढ़ती दूरी की ओर बढ़ते हैं। हम तुरंत चरणों की संख्या और चरण आकार क्यों निर्धारित करते हैं:

 n_samples = 10000; step_m = 1000; % meters distances = (1:n_samples) .* step_m; 

3. प्रत्येक चरण के लिए, हम गोलाकार और दीर्घवृत्त पर सीधी ज्यामितीय समस्या को हल करते हैं, वांछित बिंदु प्राप्त करते हैं:

 [ h_lats_rad(idx), h_lons_rad(idx) ] = Nav_haversine_direct(sp_lat_rad,... sp_lon_rad,... distances(idx),... fwd_az_rad,... el.mjsa_m); [ v_lats_rad(idx), v_lons_rad(idx), v_rev_az_rad, v_its ] = Nav_vincenty_direct(sp_lat_rad,... sp_lon_rad,... fwd_az_rad,... distances(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

4. प्रत्येक चरण के लिए, हम उलटे जियोडेसिक समस्याओं को हल करते हैं - हम एक गोले और एक दीर्घवृत्त पर प्राप्त परिणामों के बीच की दूरी की गणना करते हैं:

 [ v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(h_lats_rad(idx),... h_lons_rad(idx),... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

5. हम दोनों तरीकों के लिए उल्टे सीधे समाधानों की जाँच करते हैं:

 [ ip_v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); ip_h_dist(idx) = Nav_haversine_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el.mjsa_m); 

स्क्रिप्ट में, यह क्रम पहले एक चरण = 1000 मीटर और फिर एक चरण = 1 मीटर के लिए किया जाता है।

सबसे पहले, देखते हैं कि निर्देशांक (अक्षांश और देशांतर) में प्रत्यक्ष निर्णयों के परिणाम कैसे भिन्न होते हैं, जिसके लिए हम "डेल्टा" वैक्टर की गणना करते हैं, क्योंकि सब कुछ एक पंक्ति में मतलाब पर लिखा गया है:

 d_lat_deg = radtodeg(v_lats_rad - h_lats_rad); %    ( ) d_lon_deg = radtodeg(v_lons_rad - h_lons_rad); %    ( ) 

अक्ष पर, फरसीसा को लघुगणकीय पैमाने पर प्रदर्शित किया जाएगा, क्योंकि हमारी दूरी 1 से 10,000 किमी तक भिन्न होती है:

 figure semilogx(distances, d_lat_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Latitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); figure semilogx(distances, d_lon_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Longitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); 

परिणामस्वरूप, हमें अक्षांश के लिए ऐसे ग्राफ़ मिलते हैं:



और देशांतर के लिए:



मैं डिग्री में नहीं समझता, मुझे हमेशा "आंख से" अनुमान लगाने की विधि द्वारा निर्देशित किया जाता है:
किसी चीज़ का 1 ° औसतन 100-110 किमी होता है। और अगर त्रुटि एक मिलियन से अधिक है या कम से कम सौ हजार डिग्री का हिस्सा है - यह बुरी खबर है।

इसके बाद, हम गोले और दीर्घवृत्त के लिए सूत्रों के अनुसार प्रत्येक बिंदु पर प्राप्त बिंदु और बिंदु के बीच की दूरी को देखते हैं। हम विन्सेन्टी के सूत्रों का उपयोग करके दूरी की गणना करते हैं (क्योंकि यह स्पष्ट रूप से अधिक सटीक है - लेखक मिलीमीटर में त्रुटि का वादा करता है)। मीटर और किलोमीटर में चार्ट अधिक मूर्त और परिचित हैं:

 figure semilogx(distances, v_dist, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Endpoint difference by Vincenty)'); xlabel('Distance, m'); ylabel('Difference, m'); 

परिणामस्वरूप, हमें निम्न चित्र मिलते हैं:



यह पता चला है कि 10,000 किमी की रेंज में 10 किमी की दूरी तय करती है।

यदि अब सब कुछ एक कदम के लिए दोहराया जाता है तो 1000 गुना छोटा होता है, अर्थात। जब एक्स अक्ष के साथ पूरी रेंज 10,000 किमी नहीं है, लेकिन केवल 10 किमी है, तो चित्र निम्नानुसार है:



यानी 10 किमी की दूरी पर केवल 20 मीटर की दूरी तय की जाती है, और 1-2 मीटर के लिए सूत्र लगभग 1000 मीटर की दूरी पर ही विचरण करते हैं।

कप्तान का निष्कर्ष स्पष्ट है: यदि क्षेत्र पर समाधान के साथ सूत्रों की सटीकता समस्या के लिए पर्याप्त है, तो हम उनका उपयोग करते हैं - वे सरल और तेज हैं।

खैर, उन लोगों के लिए जिनके लिए मिलीमीटर सटीकता पर्याप्त नहीं है, 2013 में नैनोमीटर (!) सटीकता के लिए भूगर्भिक समस्याओं के समाधान का वर्णन करते हुए एक काम प्रकाशित किया गया था । मुझे यकीन नहीं है कि मैं तुरंत वहां पहुंच सकता हूं जहां इसकी आवश्यकता हो सकती है - गुरुत्वाकर्षण-लहर डिटेक्टरों का निर्माण करते समय भू-सर्वेक्षण सर्वेक्षणों को छोड़कर या पूरी तरह से शानदार)।

अब सबसे स्वादिष्ट पर चलते हैं:

नेविगेशन समस्याओं का समाधान

फिलहाल, लाइब्रेरी निर्धारित कर सकती है:

• 2 डी और 3 डी में ज्ञात निर्देशांक के साथ बिंदु से दूरी तक वस्तु का स्थान। इसे हम TOA कहते हैं - आगमन का समय (या अधिक सही ढंग से, TOF - उड़ान का समय)
• 2 डी और 3 डी में आने वाले समय में अंतर से वस्तु का स्थान। इसे हम TDOA (टाइम डिफरेंस ऑफ अराइवल) कहते हैं।

वास्तव में, हम हमेशा सिग्नल के आगमन की सीमाओं या समय को मापते हैं (और, तदनुसार, उनके अंतर) त्रुटियों के साथ, शोर के साथ। इसलिए, अधिकांश मामलों में नेविगेशन समस्याओं का समाधान त्रुटियों का न्यूनतमकरण है। कम से कम वर्ग विधि और वह सब है ।

जिसे कम करने की आवश्यकता है उसे अवशिष्ट फलन कहा जाता है।

TOA कार्यों के लिए, यह इस तरह दिखता है:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z_i_i) ^ 2 )} - r_i] ^ 2$$

जहाँ $$$\ epsilon (x, y, z)$- निर्देशांक के साथ एक निश्चित बिंदु के लिए अवशिष्ट फ़ंक्शन का मूल्य $$$(x, y, z)$; N निर्देशांक वाले नियंत्रण बिंदुओं की संख्या है $$$(x_i, y_i, z_i)$। $$$r_i$- संदर्भ बिंदुओं से निर्धारित वस्तु तक दूरी को मापा।

और इस तरह TDOA कार्यों के लिए:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1, j = 2, i \ neq j} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y- y_i) ^ 2+ (z-z_i) ^ 2)} - \\ \ sqrt {(x-x_j) ^ 2 + (y-y_j) ^ 2 + (z-z_j) ^ 2)} - \ nu (t_ {ऐ}) -t_ {अज})] ^ 2$$

यहां सब कुछ समान है, केवल संदर्भ बिंदुओं के अलग-अलग जोड़े और इसी आगमन के समय पर विचार किया जाता है $$$t_ {ऐ}$और $$$t_ {अज}$, और $$$\ n$- संकेत प्रसार गति।

और इसलिए ये फ़ंक्शन कोड में दिखते हैं:




जैसा कि आप देख सकते हैं, दोनों फ़ंक्शन नियंत्रण अंक या लाइनों की एक चर संख्या के साथ काम करते हैं। सामान्य तौर पर, कार्य अलग-अलग हो सकते हैं, और अवशिष्ट कार्य भी।

उदाहरण के लिए, आप न केवल स्थान का निर्धारण करने की समस्या को हल कर सकते हैं, बल्कि अभिविन्यास का निर्धारण भी कर सकते हैं। इस मामले में, अवशिष्ट फ़ंक्शन में एक या अधिक कोण होंगे।

आइए हम लाइब्रेरी की आंतरिक संरचना पर अधिक विस्तार से ध्यान दें

इस स्तर पर, लाइब्रेरी 2 डी और 3 डी कार्यों के साथ काम करती है और सॉल्वर खुद नहीं जानता है और यह जानना नहीं चाहता है कि न्यूनतम कार्यक्षमता क्या पसंद है। यह निम्नलिखित तरीके से प्राप्त किया जाता है।

सॉल्वर के दो पहलू होते हैं: 2 डी और 3 डी सॉलर्स , नेल्डर-मीड विधि के आधार पर या, जैसा कि इसे सिम्पलेक्स विधि भी कहा जाता है।

चूँकि इस विधि में व्युत्पत्ति की गणना (तथाकथित व्युत्पन्न-मुक्त न्यूनतमकरण ) की आवश्यकता नहीं होती है, आदर्श रूप से, पुस्तकालय उपयोगकर्ता यदि आवश्यक हो तो अपने स्वयं के अवशिष्ट कार्यों का उपयोग कर सकता है। साथ ही, सैद्धांतिक रूप से समस्या को हल करने में उपयोग किए जाने वाले नियंत्रण बिंदुओं की संख्या पर कोई ऊपरी सीमा नहीं है।

C # और Rust में, 2D और 3D सॉल्वर जेनेरिक तरीके हैं:

 public static void NLM2D_Solve<T>(Func<T[], double, double, double, double> eps, T[] baseElements,... //       : fxi[0] = eps(baseElements, xix[0], xiy[0], z); 

सॉल्वर को खुद बुलाने का एक उदाहरण:

 public static void TOA_NLM2D_Solve(TOABasePoint[] basePoints, double xPrev, double yPrev, double z, int maxIterations, double precisionThreshold, double simplexSize, out double xBest, out double yBest, out double radialError, out int itCnt) { NLM2D_Solve<TOABasePoint>(Eps_TOA3D, basePoints, xPrev, yPrev, z, maxIterations, precisionThreshold, simplexSize, out xBest, out yBest, out radialError, out itCnt); } 

जंग पर ...

 pub fn nlm_2d_solve<T>(eps: Eps3dFunc<T>, base_elements: &Vec<T>... 

सब कुछ समान है, भाषा के वाक्य-विन्यास के लिए सटीक है।

माटेलाबे में, अंतर्निहित स्वैच्छिकता के साथ, सॉल्वर को खुद पता नहीं है कि उसके लिए कौन से मूल तत्व पारित किए गए हैं - उपयोगकर्ता को स्वयं यह सुनिश्चित करना होगा कि अवशिष्ट फ़ंक्शन का लिंक और सॉल्वर को दिए गए समर्थन तत्वों के सेट संगत हैं:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(eps, base_elements, .... 

और तदनुसार, सॉल्वर को कॉल इस तरह दिखता है:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size) [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(@Nav_eps_toa3d, base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size); end 

टीओए और टीडीओए समस्याओं के समाधान को प्रदर्शित करने के लिए एक विशेष मटलब स्क्रिप्ट है।

2D में प्रदर्शन को संयोग से नहीं चुना गया था - मुझे यकीन नहीं है कि मैं यह पता लगा सकता हूं कि कैसे तीन आयामी अवशिष्ट फ़ंक्शन को बस और सूचनात्मक रूप से प्रदर्शित किया जाए =)

So. स्क्रिप्ट की शुरुआत में ऐसे पैरामीटर हैं जिन्हें बदला जा सकता है:

 %% parameters n_base_points = 4; %    area_width_m = 1000; %   max_depth_m = 100; %   ( Z) propagation_velocity = 1500;%     -  max_iterations = 2000; %    precision_threshold = 1E-9; %   simplex_size = 1; %      contour_levels = 32; %      range_measurements_error = 0.01; % 0.01 means 1% of corresponding slant range %    -   1% 

वांछित बिंदु की स्थिति को निर्दिष्ट क्षेत्र में बेतरतीब ढंग से सेट किया गया है:

 %% actual target location r_ = rand * area_width_m / 2; az_ = rand * 2 * pi; actual_target_x = r_ * cos(az_); actual_target_y = r_ * sin(az_); actual_target_z = rand * max_depth_m; 

इसके बाद, नियंत्रण बिंदुओं को बेतरतीब ढंग से रखें, वांछित से दूरी की गणना करें और सब कुछ प्रदर्शित करें:

 %% base points figure hold on grid on base_points = zeros(n_base_points, 4); for n = 1:n_base_points r_ = area_width_m / 2 - rand * area_width_m / 4; az_ = (n - 1) * 2 * pi / n_base_points; base_x = r_ * cos(az_); base_y = r_ * sin(az_); base_z = rand * max_depth_m; dist_to_target = Nav_dist_3d(base_x, base_y, base_z, actual_target_x, actual_target_y, actual_target_z); base_points(n, :) = [ base_x base_y base_z dist_to_target ]; end N =1:n_base_points; plot3(actual_target_x, actual_target_y, actual_target_z,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot3(base_points(N, 1), base_points(N, 2), base_points(N, 3),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); for n = 1:n_base_points line([ actual_target_x, base_points(n, 1) ], [ actual_target_y, base_points(n, 2) ], [ actual_target_z, base_points(n, 3) ]); end view(45, 15); legend('target', 'base points'); title('Placement of base stations and the target'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); zlabel('Z coordinate, m'); 

परिणामस्वरूप, हमें निम्न चित्र मिलते हैं:



दूरी माप में यादृच्छिक त्रुटियां जोड़ें:

 % adding range measurement errors base_points(N, 4) = base_points(N, 4) + base_points(N, 4) *... (rand * range_measurements_error - range_measurements_error / 2); 

हम एक निश्चित परिसीमन के साथ चयनित क्षेत्र के लिए अवशिष्ट कार्य का निर्माण करते हैं - अन्यथा, गणना ध्यान देने योग्य समय ले सकती है। मैंने क्षेत्र का आकार 1000 x 1000 मीटर चुना है और मैं 10 मीटर के बाद पूरे क्षेत्र में अवशिष्ट कार्य मानता हूं:

 % error surface tiles tile_size_m = 10; n_tiles = area_width_m / tile_size_m; %% TOA solution error_surface_toa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_toa(t_x, t_y) = Nav_eps_toa3d(base_points,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf_a = [1:n_tiles] * tile_size_m - area_width_m / 2; surf(surf_a, surf_a, error_surface_toa); title('TOA solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

यहाँ अवशिष्ट कार्य है:



बेशक, मैं थोड़ा चालाक था - नियंत्रण बिंदुओं के सापेक्ष स्थान और वांछित एक को चुना जाता है ताकि वे हमेशा अंदर वांछित बिंदु के साथ एक उत्तल आकृति बना सकें। मोटे तौर पर इसके कारण, सतह में एक न्यूनतम है, जो बिना किसी समस्या के है।

एक अभिमानी पाठक चीजों के इस क्रम को बदल सकता है और दुर्घटना से लंगर बिंदुओं और वांछित को सेट करने का प्रयास कर सकता है।

अब इसे सभी मिलकर प्रदर्शित करें। यह सतह पर करना मुश्किल है - ऊर्ध्वाधर अक्ष के साथ अलग-अलग मूल्य। इसलिए, दो-आयामी स्लाइस पर सब कुछ खींचना सुविधाजनक है:

 figure hold on contourf(surf_a, surf_a, error_surface_toa, contour_levels); plot(actual_target_x, actual_target_y,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(base_points(N, 1), base_points(N, 2),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); [ x_prev, y_prev ] = Nav_toa_circles_1d_solve(base_points, actual_target_z, pi / 180, 10, 0.1); [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, actual_target_z,... max_iterations, precision_threshold, simplex_size); plot(x_best, y_best,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); title(sprintf('TOA Solution: Residual function. Target location estimated with E_{radial} = %.3f m in %d iterations', rerr, it_cnt)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Residual function value', 'Actual target location', 'Base points', 'Estimated target location'); 

परिणाम कुछ इस प्रकार है:



रेडियल त्रुटि को ग्राफ़ हेडर में प्रदर्शित किया जाता है - अवशिष्ट फ़ंक्शन के अंतिम मूल्य की जड़। ग्राफ दिखाता है कि वास्तविक स्थान और गणना की गई गणना अच्छे समझौते में हैं, लेकिन पैमाने हमें यह निर्धारित करने की अनुमति नहीं देते हैं कि कितनी अच्छी तरह से है।

इसलिए, हम वांछित बिंदु की गणना स्थान और उसके वास्तविक स्थान को अलग-अलग प्रदर्शित करते हैं और उनके बीच की दूरी की गणना करते हैं:

 figure hold on grid on dx = actual_target_x - x_best; dy = actual_target_y - y_best; plot(0, 0,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(dx, dy,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); plot(-dx * 2, -dy * 2, '.w'); plot(dx * 2, dy * 2, '.w'); d_delta = Nav_dist_3d(actual_target_x, actual_target_y, actual_target_z, x_best, y_best, actual_target_z); title(sprintf('TOA Solution: Actual vs. Estimated location, distance: %.3f m', d_delta)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Actual target location', 'Estimated target location'); 

यहाँ यह कैसा दिखता है:



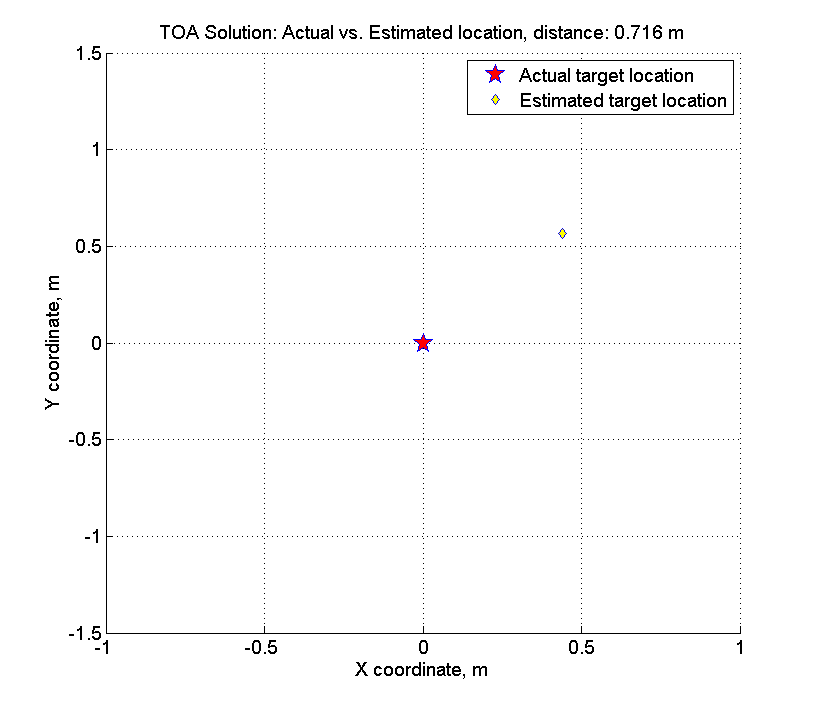
याद रखें कि हमारे पास एक यादृच्छिक त्रुटि का आयाम है - रेंज का 1%, औसतन, सीमा ~ 200-400 मीटर है, अर्थात। त्रुटि आयाम लगभग 2-4 मीटर है। समाधान की खोज करते समय, हमने केवल 70 सेंटीमीटर की गलती की।

अब, सादृश्य द्वारा, उसी डेटा पर TDOA समस्या को हल करने का प्रयास करते हैं। ऐसा करने के लिए, हम यह दिखावा करेंगे कि हम केवल संकेत बिंदुओं के वांछित बिंदु से संदर्भ बिंदुओं तक पहुंचने के समय को जानते हैं (या इसके विपरीत, इससे कोई फर्क नहीं पड़ता) - हम केवल संकेत प्रसार की गति से अपनी दूरी को विभाजित करते हैं - केवल आपके अंतर और पूर्ण मान महत्वपूर्ण नहीं हैं।

 % since TDOA works with time difference of arriaval, % we must recalculate base point's distances to times base_points(N,4) = base_points(N,4) / propagation_velocity; base_lines = Nav_build_base_lines(base_points, propagation_velocity); 

त्रुटियों की सतह बनाएँ और ड्रा करें:

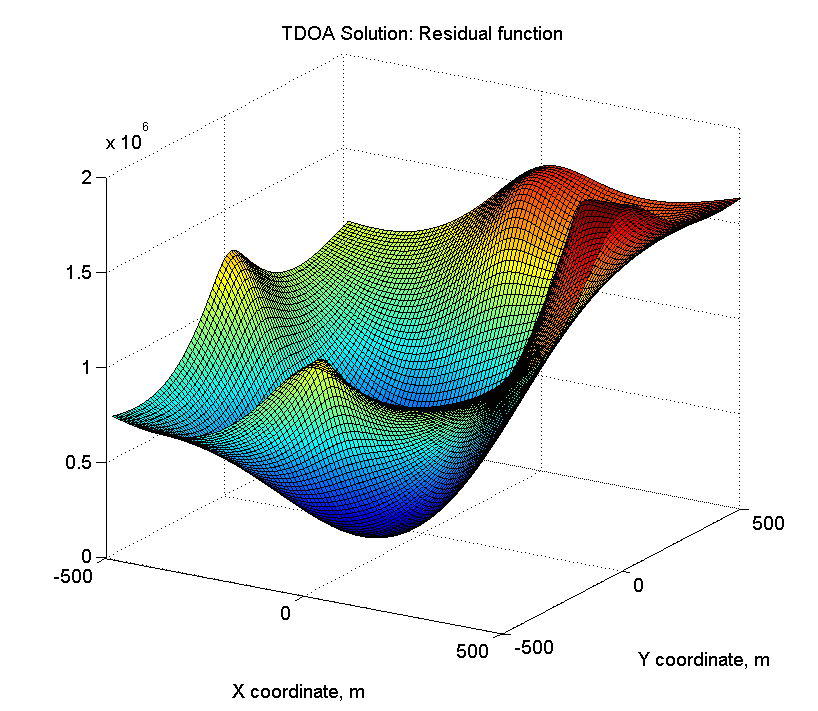
 error_surface_tdoa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_tdoa(t_x, t_y) = Nav_eps_tdoa3d(base_lines,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf(surf_a, surf_a, error_surface_tdoa); title('TDOA Solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

यह कुछ इस तरह से निकलता है:



और संदर्भ बिंदुओं के साथ ऊपर से दृश्य, वांछित बिंदु की वास्तविक और गणना की गई स्थिति:



और अधिक विस्तार से, वास्तविक और गणना किए गए स्थान के बीच विसंगति:



इस विशेष मामले में, टीडीओए समाधान टीओए समाधान से भी बेहतर निकला - पूर्ण त्रुटि 0.3 मीटर है।

मॉडल में अच्छा - आप हमेशा यह जानते हैं कि वास्तव में वांछित बिंदु कहाँ स्थित है। यह हवा में बदतर है - शायद कई बिंदु हैं, पानी के नीचे आपने अभी कुछ गणना की है और सभी - 99% मामलों में, वास्तविक स्थान से विचलन की गणना करने के लिए, यह (इस स्थान) भी पहले गणना की जानी चाहिए।

अब, एक निष्कर्ष के रूप में, हम अपने नए ज्ञान को जियोडेटिक और नेविगेशन कार्यों के बारे में संयोजित करेंगे।

अंतिम राग

वास्तविक जीवन में स्थिति के जितना संभव हो उतना करीब:

• मान लीजिए कि हमारे संदर्भ बिंदुओं में अंतर्निहित जीएनएसएस रिसीवर हैं और हम केवल उनके भौगोलिक निर्देशांक जानते हैं
• ऊर्ध्वाधर समन्वय हमारे लिए अज्ञात है (3D समस्या)
• हम वांछित या इसके विपरीत संदर्भ बिंदुओं से संकेत के केवल आगमन के समय को मापते हैं

इस स्थिति को तीनों कार्यान्वयनों में सबसे हालिया परीक्षण में वर्णित किया गया है। मैं किसी तरह से जंग से वंचित हूं, और मैं इस पर अंतिम उदाहरण का विश्लेषण करूंगा।

तो, पुस्तकालय में सबसे हाल ही में परीक्षण। वांछित बिंदु के निर्देशांक के रूप में, मैंने पार्क में एक जगह चुनी, जहां मैं अक्सर कुत्ते के साथ चलता हूं।

 #[test] fn test_tdoa_locate_3d() { let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); let base_number = 4; // 4   let start_base_z_m: f64 = 1.5; //  Z     let base_z_step_m = 5.0; //        5  let actual_target_lat_deg: f64 = 48.513724 // singed degrees let actual_target_lon_deg: f64 = 44.553248; // signed degrees let actual_target_z_m: f64 = 25.0; // meters - ,    ! // generate base points via Vincenty equations let mut base_points = Vec::new(); let start_dst_projection_m = 500.0; //      500  let dst_inc_step_m = 50.0; //   -  50   // azimuth step let azimuth_step_rad = PI2 / base_number as f64; //     let actual_target_lat_rad = actual_target_lat_deg.to_radians(); let actual_target_lon_rad = actual_target_lon_deg.to_radians(); // signal propagation speed let velocity_mps = 1450.0; // m/s,        //     for base_idx in 0..base_number { //        let dst_projection_m = start_dst_projection_m + dst_inc_step_m * base_idx as f64; //       let azimuth_rad = azimuth_step_rad * base_idx as f64; //        Vincenty let vd_result = vincenty_direct(actual_target_lat_rad, actual_target_lon_rad, azimuth_rad, dst_projection_m, &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); //   Z let base_z_m = start_base_z_m + base_z_step_m * base_idx as f64; //        let dz_m = actual_target_z_m - base_z_m; //      let slant_range_m = (dst_projection_m * dst_projection_m + dz_m * dz_m).sqrt(); //   .          Rust   ! base_points.push((vd_result.0.to_degrees(), vd_result.1.to_degrees(), base_z_m, slant_range_m / velocity_mps)); } //     -   NAN- let lat_prev_deg = f64::NAN; let lon_prev_deg = f64::NAN; let prev_z_m = f64::NAN; //   let tdoa_3d_result = tdoa_locate_3d(&base_points, lat_prev_deg, lon_prev_deg, prev_z_m, NLM_DEF_IT_LIMIT, NLM_DEF_PREC_THRLD, 10.0, &el, velocity_mps); //          let vi_result = vincenty_inverse(actual_target_lat_rad, actual_target_lon_rad, tdoa_3d_result.0.to_radians(), tdoa_3d_result.1.to_radians(), &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); assert!(vi_result.0 < start_dst_projection_m * 0.01, "Estimated location is farer than limit (1%): {}", vi_result.0); assert_approx_eq!(tdoa_3d_result.2, actual_target_z_m, start_dst_projection_m * 0.05); assert!(tdoa_3d_result.3 < start_dst_projection_m * 0.01, "Residual function greater than limit (1%): {}", tdoa_3d_result.3); assert!(tdoa_3d_result.4 < NLM_DEF_IT_LIMIT, "Method did not converge: iterations limit exeeded {}", tdoa_3d_result.4); } 

परिणामस्वरूप, हमारे पास:
वास्तविक स्थान (लैट, लोन, जेड): 48.513724 44.553248 25
परिकलित स्थिति (लैट, लोन, जेड): 48.513726 44.553252 45.6
सतह पर बिंदुओं के बीच की दूरी (एम): 0.389
Z निर्देशांक (m) में अंतर: 20.6

"योजना" मैच बहुत अच्छा है, त्रुटि केवल 40 सेंटीमीटर है, और ऊर्ध्वाधर समन्वय 20 मीटर है। ऐसा क्यों हो रहा है, मुझे लगता है कि पाठकों को लगता है =)

पुनश्च

वर्णित पुस्तकालय एक विशुद्ध रूप से शैक्षिक परियोजना है, जिसे मैं आगे विकसित करने और फिर से भरने की योजना बना रहा हूं। योजनाओं में सी में कार्यान्वयन और व्यापक दस्तावेज लिखना शामिल है।

इस पर, मुझे अपना ध्यान रखने दें, आपके ध्यान के लिए धन्यवाद।मैं किसी भी प्रतिक्रिया के लिए असीम रूप से खुश रहूंगा।
आशा है कि लेख और पुस्तकालय सहायक होंगे।
किसी भी त्रुटि (व्याकरणिक और तार्किक) की रिपोर्ट करें - मैं इसे सही करूंगा।

पी पी एस

बस के मामले में, यहाँ ऑनलाइन (और न केवल) मैटलैब / ऑक्टेव दुभाषियों की एक कड़ी है, जिसका उपयोग मैं स्वयं करता हूं:

• ऑनलाइन ऑक्टेव कंपाइलर
• ऑक्टेव ऑनलाइन
• GNU ऑक्टेव