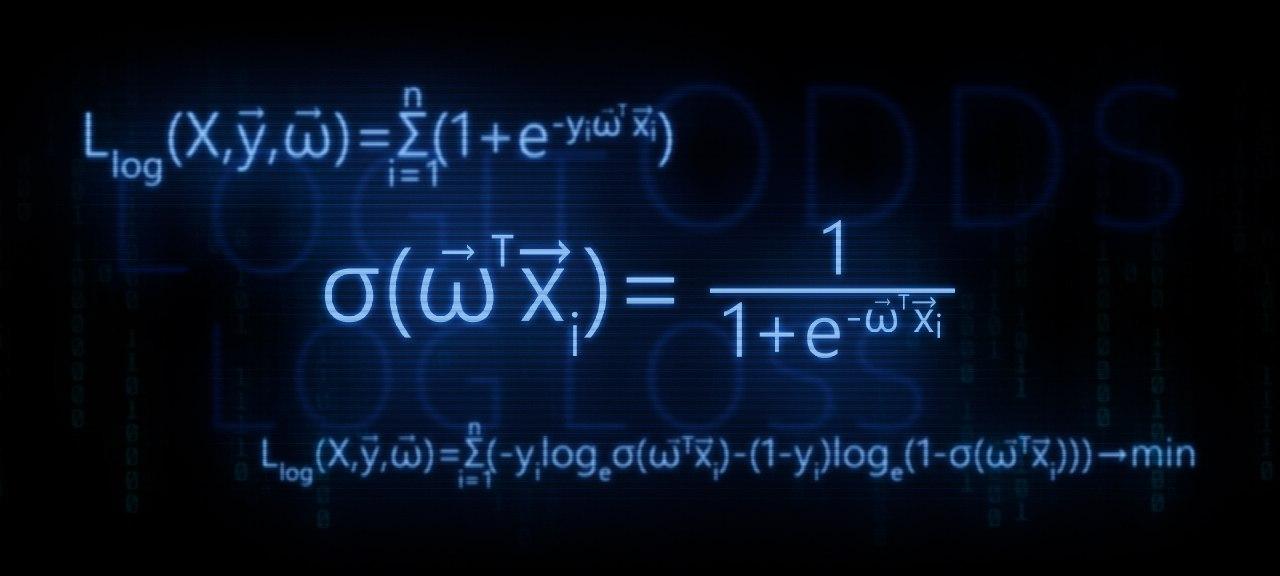
इस आलेख में, हम
रैखिक प्रतिगमन फ़ंक्शन को व्युत्क्रम लॉग ट्रांसफ़ॉर्मेशन फ़ंक्शन (दूसरे शब्दों में, लॉजिस्टिक प्रतिक्रिया फ़ंक्शन) में परिवर्तित करने के सैद्धांतिक गणना का विश्लेषण करेंगे। फिर,
अधिकतम संभावना विधि के शस्त्रागार का उपयोग करते हुए, लॉजिस्टिक रिग्रेशन मॉडल के अनुसार, हम नुकसान फ़ंक्शन
लॉजिस्टिक लॉस को प्राप्त करते हैं, या दूसरे शब्दों में, हम उस फ़ंक्शन को निर्धारित करते हैं जिसके द्वारा लॉजिस्टिक रिग्रेशन मॉडल में वेट वेक्टर के मापदंडों का चयन किया जाता है।
v e c w ।
लेख की रूपरेखा:
- चलो दो चर के बीच सीधा संबंध के बारे में दोहराते हैं
- हम रैखिक प्रतिगमन समारोह को परिवर्तित करने की आवश्यकता की पहचान करते हैं f ( w , x i ) = v e c w T v e c x i रसद प्रतिक्रिया समारोह के लिए \ sigma (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {- \ vec {w} ^ T \ vec {x_i}}\ sigma (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {- \ vec {w} ^ T \ vec {x_i}}
- हम परिवर्तनों को पूरा करते हैं और लॉजिस्टिक रिस्पांस फ़ंक्शन प्राप्त करते हैं
- आइए यह समझने की कोशिश करें कि मापदंडों को चुनते समय सबसे कम वर्ग विधि क्यों खराब है vecw लॉजिस्टिक लॉस फीचर्स
- हम पैरामीटर चयन फ़ंक्शन को निर्धारित करने के लिए अधिकतम संभावना विधि का उपयोग करते हैं vecw :
5.1। केस 1: वर्ग पदनाम 0 और 1 के साथ वस्तुओं के लिए लॉजिस्टिक लॉस फ़ंक्शन:
L_ {लॉग} (X, \ vec {y}, \ vec {w}) = \ _ \ _ limit_ {i = 1} ^ n (-y_i \ mkern 2mu log_e \ mkern 5mu \ sigma (\ vec {w}) ^ T \ vec {x_i}) - (1-y_i) \ mkern 2mu log_e \ mkern 5mu (1 - \ sigma (\ vec {w} ^ T \ vec [x_i}))) \ rightarrow min
5.2। केस 2: कक्षा पदनाम -1 और +1 वाले ऑब्जेक्ट के लिए लॉजिस्टिक लॉस फ़ंक्शन:
L_ {लॉग} (X, \ vec {y}, \ vec {w}) = \ _ \ _ limit_ {i = 1} ^ n \ mkern 2mu log_e \ mkern 5mu (1 + ^ ^) - - y_i \ vec { w} ^ T \ vec {x_i}}) \ rightarrow min
लेख सरल उदाहरणों से भरा हुआ है जिसमें सभी गणना मौखिक रूप से या कागज पर करना आसान है, कुछ मामलों में कैलकुलेटर की आवश्यकता हो सकती है। तो तैयार हो जाइए :)
यह आलेख मशीन लर्निंग की मूल बातें में प्रारंभिक स्तर के ज्ञान के साथ डेटाविंटिस्टों पर अधिक लक्षित है।
आलेख ड्राइंग रेखांकन और गणना के लिए कोड भी प्रदान करेगा। सभी कोड
अजगर 2.7 में लिखे गए हैं। मैं उपयोग किए गए संस्करण के "नवीनता" के बारे में पहले से समझाता हूं - यह ऑनलाइन शिक्षा
कौरसेरा के लिए कोई कम प्रसिद्ध ऑनलाइन मंच पर
यैंडेक्स से एक प्रसिद्ध पाठ्यक्रम लेने के लिए शर्तों में से एक है, और, जैसा कि आप मान सकते हैं, सामग्री इस पाठ्यक्रम के आधार पर तैयार की गई थी।
01. सीधी रेखा
सवाल पूछना काफी उचित है - सीधा रिश्ता और लॉजिस्टिक रिग्रेशन कहां है?
सब कुछ सरल है! लॉजिस्टिक रिग्रेशन उन मॉडलों में से एक है जो लीनियर क्लासिफायरियर से संबंधित हैं। सरल शब्दों में, एक रैखिक क्लासिफायरियर का उद्देश्य लक्ष्य मूल्यों की भविष्यवाणी करना है
य चर (रजिस्टरों) से
X । यह माना जाता है कि संकेतों के बीच संबंध
X और लक्ष्य मान
य रैखिक। इसलिए क्लासिफायर का नाम ही रैखिक है। बहुत मोटे तौर पर सामान्यीकृत, लॉजिस्टिक रिग्रेशन मॉडल इस धारणा पर आधारित है कि सुविधाओं के बीच एक रैखिक संबंध है
X और लक्ष्य मान
य । यहाँ यह है - एक कनेक्शन।
अध्ययनित मात्राओं की सीधी निर्भरता के बारे में स्टूडियो पहला उदाहरण है, और ठीक ही ऐसा है। लेख तैयार करने की प्रक्रिया में, मैं एक उदाहरण के सामने आया, जो पहले से ही
गले में खराश हो गया है - वोल्टेज पर वर्तमान ताकत की निर्भरता
("एप्लाइड रिग्रेशन एनालिसिस", एन ड्रेपर, जी स्मिथ) । यहां हम इस पर भी विचार करेंगे।
ओम के नियम के अनुसार:I=U/R जहाँ
मैं - वर्तमान ताकत
यू - वोल्टेज
आर - प्रतिरोध।
यदि हम
ओह्म के नियम को नहीं जानते हैं, तो हम बदलकर निर्भरता को अनुभवपूर्वक पा सकते हैं
यू और मापने
मैं समर्थन करते हुए
आर तय की। तब हम देखेंगे कि निर्भरता ग्राफ
मैं से
यू मूल से गुजरने वाली कम या ज्यादा सीधी रेखा देता है। हमने कहा "अधिक या कम", क्योंकि, निर्भरता वास्तव में सटीक है, हमारे माप में छोटी त्रुटियां हो सकती हैं, और इसलिए ग्राफ़ पर अंक बिल्कुल रेखा पर नहीं गिर सकते हैं, लेकिन इसके चारों ओर बेतरतीब ढंग से बिखरे होंगे।
चार्ट 1 "निर्भरता
मैं से
यू "
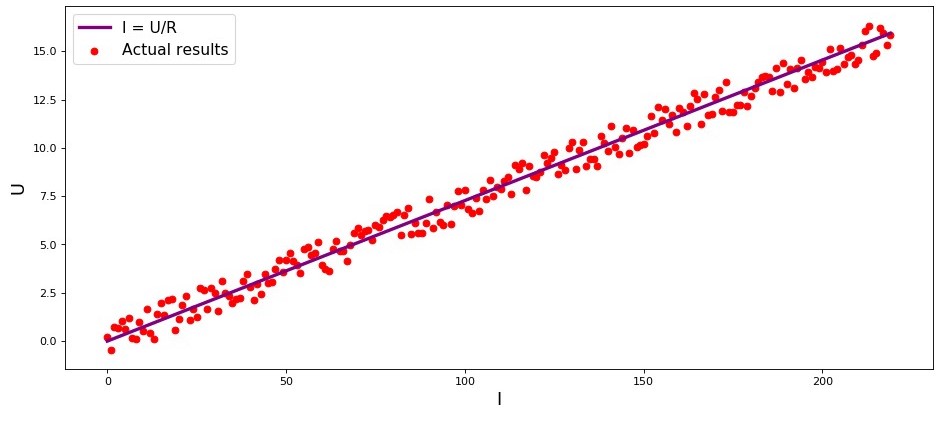
ग्राफ प्रतिपादन कोडimport matplotlib.pyplot as plt %matplotlib inline import numpy as np import random R = 13.75 x_line = np.arange(0,220,1) y_line = [] for i in x_line: y_line.append(i/R) y_dot = [] for i in y_line: y_dot.append(i+random.uniform(-0.9,0.9)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R') plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results') plt.xlabel('I', size = 16) plt.ylabel('U', size = 16) plt.legend(prop = {'size': 14}) plt.show()
02. रैखिक प्रतिगमन समीकरण के परिवर्तनों की आवश्यकता
एक अन्य उदाहरण पर विचार करें। कल्पना करें कि हम एक बैंक में काम करते हैं और हमें कुछ कारकों के आधार पर, एक उधारकर्ता द्वारा ऋण चुकाने की संभावना निर्धारित करने के कार्य का सामना करना पड़ता है। कार्य को सरल बनाने के लिए, हम केवल दो कारकों पर विचार करते हैं: उधारकर्ता का मासिक वेतन और ऋण के पुनर्भुगतान के लिए मासिक भुगतान।
कार्य बहुत सशर्त है, लेकिन इस उदाहरण से हम समझ सकते हैं कि इसे हल करने के लिए
रैखिक प्रतिगमन फ़ंक्शन का उपयोग
करना पर्याप्त क्यों नहीं है, और हम यह भी पता लगाएंगे कि फ़ंक्शन के साथ क्या परिवर्तन करना आवश्यक है।
हम उदाहरण के लिए लौटते हैं। यह समझा जाता है कि वेतन जितना अधिक होगा, उतनी अधिक उधारकर्ता मासिक को ऋण चुकाने के लिए निर्देशित कर सकेगा। उसी समय, वेतन की एक निश्चित सीमा के लिए, यह निर्भरता खुद के लिए काफी रैखिक होगी। उदाहरण के लिए, 60,000 200 to ००० supp पर वेतन सीमा लें और मान लें कि वेतन की इंगित सीमा में, वेतन की राशि पर मासिक भुगतान के आकार की निर्भरता रैखिक है। मान लीजिए, मजदूरी की निर्दिष्ट सीमा के लिए, यह पता चला था कि भुगतान के वेतन का अनुपात 3 से नीचे नहीं जा सकता है और उधारकर्ता के पास अभी भी 5.000 आरआई आरक्षित होना चाहिए। और केवल इस मामले में, हम मान लेंगे कि उधारकर्ता बैंक को ऋण वापस कर देगा। फिर, रेखीय प्रतिगमन समीकरण रूप लेता है:
f (w, x_i) = w_0 + w_1x_ {i1} + w_2x_ {i_},जहाँ
w0=−5.000 ।
w1=1 ।
w2=−3 ।
xi1 -
वेतन मैं मई के ऋण लेने वाले
xi2 -
ऋण भुगतान मैं मई के ऋण लेने वाले।
समीकरण में निश्चित मापदंडों के साथ वेतन और ऋण भुगतान को प्रतिस्थापित करना
vecw आप यह तय कर सकते हैं कि ऋण देना या मना करना है या नहीं।
आगे देखते हुए, हम ध्यान दें कि, दिए गए मापदंडों के लिए
vecw लॉजिस्टिक रिस्पांस फ़ंक्शन में उपयोग किए जाने
वाले रैखिक रिग्रेशन फ़ंक्शन बड़े मानों का उत्पादन करेगा जो ऋण चुकौती की संभावनाओं की गणना करना मुश्किल बनाते हैं। इसलिए, हमारे गुणांक को कम करने का प्रस्ताव है, मान लीजिए, 25,000 बार। इस अनुपात में परिवर्तन से, ऋण देने का निर्णय नहीं बदलेगा। हमें इस क्षण को भविष्य के लिए याद रखना चाहिए, और अब यह स्पष्ट करने के लिए कि हम किस बारे में बात कर रहे हैं, हम तीन अन्य वित्तीय उधारकर्ताओं के साथ स्थिति पर विचार करेंगे।
तालिका 1 "संभावित उधारकर्ता"
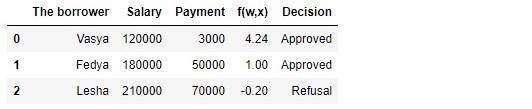
तालिका बनाने के लिए कोड import pandas as pd r = 25000.0 w_0 = -5000.0/r w_1 = 1.0/r w_2 = -3.0/r data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 'Salary':np.array([120000,180000,210000]), 'Payment':np.array([3000,50000,70000])} df = pd.DataFrame(data) df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2 decision = [] for i in df['f(w,x)']: if i > 0: dec = 'Approved' decision.append(dec) else: dec = 'Refusal' decision.append(dec) df['Decision'] = decision df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
तालिका के अनुसार, 120.000 the वेतन के साथ, वास्या, ऐसा ऋण प्राप्त करना चाहती है ताकि उसे 3.000 ः मासिक पर चुकाना पड़े। हमने निर्धारित किया कि ऋण को स्वीकृत करने के लिए, वासियों का वेतन भुगतान के आकार का तीन गुना होना चाहिए, और इसलिए कि अभी भी 5.000P होगा। वास्य ने इस आवश्यकता को पूरा किया:
120.000−3∗3.000−5.000=106.000 । वहाँ भी 106,000P रहता है। इस तथ्य के बावजूद कि गणना करते समय
च(w,xi) हमने बाधाओं को कम किया
vecw 25,000 बार, परिणाम समान था - ऋण को मंजूरी दी जा सकती है। फेडिया को भी ऋण मिलेगा, लेकिन लेसा, इस तथ्य के बावजूद कि उसे सबसे अधिक प्राप्त होता है, उसे अपनी भूख को रोकना होगा।
आइए इस मामले के लिए एक कार्यक्रम बनाएं।
चार्ट 2 "उधारकर्ताओं का वर्गीकरण"
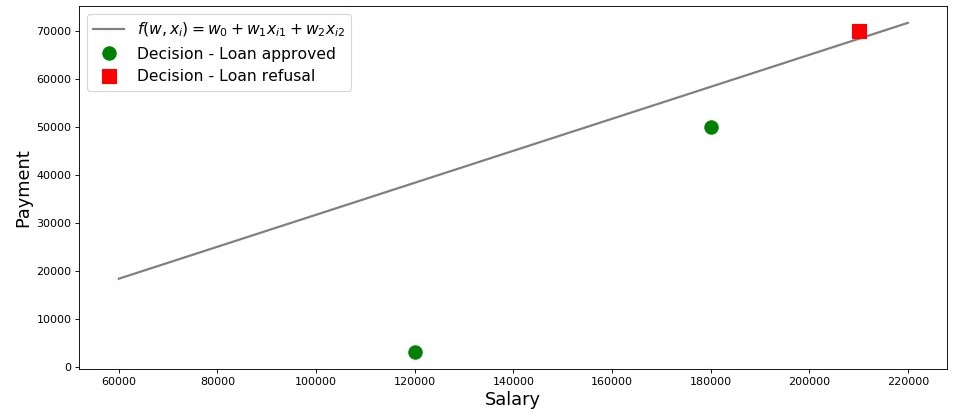
साजिश रचने का कोड salary = np.arange(60000,240000,20000) payment = (-w_0-w_1*salary)/w_2 fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$') plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 'o', color ='green', markersize = 12, label = 'Decision - Loan approved') plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 's', color = 'red', markersize = 12, label = 'Decision - Loan refusal') plt.xlabel('Salary', size = 16) plt.ylabel('Payment', size = 16) plt.legend(prop = {'size': 14}) plt.show()
तो, हमारी लाइन, फ़ंक्शन के अनुसार निर्मित
f(w,xi)=w0+w1xi1+w2xi2 , "अच्छे" से "बुरे" उधारकर्ताओं को अलग करता है। जिन उधारकर्ताओं की इच्छाएं अवसरों के साथ मेल नहीं खाती हैं, वे सीधी रेखा (लेसहा) से ऊपर हैं, जो हमारे मॉडल के मापदंडों के अनुसार ऋण चुकाने में सक्षम हैं, वे सीधी रेखा (वास्या और फेड्या) के तहत हैं। अन्यथा, हम यह कह सकते हैं - हमारी रेखा उधारकर्ताओं को दो वर्गों में विभाजित करती है। हम उन्हें निम्नानुसार दर्शाते हैं: वर्ग के लिए
+1 उन उधारकर्ताओं को वर्गीकृत करें जो वर्ग को ऋण चुकाने की संभावना रखते हैं
−1 या
0 हम उन उधारकर्ताओं को असाइन करेंगे जो सबसे अधिक संभावना है कि ऋण चुकाने में सक्षम नहीं होंगे।
इस सरल उदाहरण से निष्कर्ष को सारांशित करें। एक बिंदु लो
M(x1,x2) और, रेखा के संगत समीकरण में बिंदु के निर्देशांक को प्रतिस्थापित करता है
f(w,xi)=w0+w1xi1+w2xi2 , तीन विकल्पों पर विचार करें:
- यदि बिंदु रेखा के नीचे है, और हम इसे कक्षा में असाइन करते हैं +1 , फिर फ़ंक्शन का मान f(w,xi)=w0+w1xi1+w2xi2 से सकारात्मक होगा 0 को + infty । इसलिए हम यह मान सकते हैं कि ऋण चुकौती की संभावना भीतर है (0.5,1] । फ़ंक्शन का मान जितना अधिक होगा, संभावना उतनी ही अधिक होगी।
- यदि बिंदु रेखा के ऊपर है और हम इसे कक्षा से संबंधित करते हैं −1 या 0 , तब फ़ंक्शन का मान इससे ऋणात्मक होगा 0 को − infty । तब हम मानेंगे कि ऋण चुकौती की संभावना भीतर है [0,0.5) और, फंक्शन मोडुलो का मान जितना बड़ा होगा, हमारा आत्मविश्वास उतना ही अधिक होगा।
- बिंदु एक सीधी रेखा पर, दो वर्गों के बीच की सीमा पर है। इस मामले में, फ़ंक्शन का मान f(w,xi)=w0+w1xi1+w2xi2 बराबर होगा 0 और ऋण के पुनर्भुगतान की संभावना है 0.5 ।
अब, कल्पना कीजिए कि हमारे पास दो कारक नहीं हैं, लेकिन दसियों, उधारकर्ता तीन नहीं, बल्कि हजारों हैं। फिर एक सीधी रेखा के बजाय हमारे पास एक
आयामी आयामी विमान और गुणांक होंगे
w हमें छत से नहीं लिया जाएगा, बल्कि सभी नियमों के अनुसार वापस ले लिया जाएगा, लेकिन ऋण लेने वालों पर संचित डेटा के आधार पर, जिन्होंने ऋण वापस किया या वापस नहीं किया। और वास्तव में, आपका मन करता है, अब हम पहले से ज्ञात अनुपात वाले उधारकर्ताओं का चयन कर रहे हैं
w । वास्तव में, लॉजिस्टिक रिग्रेशन मॉडल का कार्य मापदंडों को निर्धारित करने के लिए ठीक है
w जिस पर नुकसान फ़ंक्शन
लॉजिस्टिक लॉस का मूल्य न्यूनतम हो जाएगा। लेकिन वेक्टर की गणना कैसे की जाती है
vecw , हम अभी भी लेख के 5 वें भाग में पाते हैं। इस बीच, हम अपने बैंकर और अपने तीन ग्राहकों को दिए गए वादे के मुताबिक लौट आए।
कार्य करने के लिए धन्यवाद
f(w,xi)=w0+w1xi1+w2xi2 हम जानते हैं कि किसे ऋण दिया जा सकता है, और जिसे अस्वीकार करने की आवश्यकता है। लेकिन आप ऐसी जानकारी के साथ निदेशक के पास नहीं जा सकते, क्योंकि वे हमारे द्वारा प्रत्येक उधारकर्ता से ऋण के पुनर्भुगतान की संभावना प्राप्त करना चाहते थे। क्या करें? जवाब सरल है - हमें किसी तरह फ़ंक्शन को बदलने की आवश्यकता है
f(w,xi)=w0+w1xi1+w2xi2 जिनके मूल्य सीमा में हैं
(− infty,+ infty) एक समारोह में जिसका मान सीमा में होगा
[0,1] । और ऐसा फ़ंक्शन मौजूद है, इसे
लॉजिस्टिक प्रतिक्रिया फ़ंक्शन या रिवर्स-लॉगिट रूपांतरण कहा जाता है। मिलना
\ सिग्मा (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {- \ vec {w} ^ T \ vec {x_i}}
आइए
, लॉजिस्टिक रिस्पांस फ़ंक्शन को प्राप्त करने के चरणों पर एक नज़र डालें। ध्यान दें कि हम विपरीत दिशा में कदम रखेंगे, अर्थात्। हम मानते हैं कि हम संभाव्यता का मूल्य जानते हैं, जो कि सीमा में है
0 को
1 और फिर हम संख्याओं की संपूर्ण सीमा पर इस मान को "स्पिन" करेंगे
− infty को
+ infty ।
03. लॉजिस्टिक रिस्पांस फ़ंक्शन को आउटपुट करता है
चरण 1. संभावना मानों को सीमा में स्थानांतरित करें [0,+ infty)
फ़ंक्शन परिवर्तन के समय
f(w,xi)=w0+w1xi1+w2xi2 रसद प्रतिक्रिया समारोह के लिए \ सिग्मा (\ vec {w} ^ T \ vec {x_i}) = \ frac {1} {1 + e ^ {\ vec {w} ^ T \ vec {x_i}} हम अपने क्रेडिट विश्लेषक को अकेले छोड़ देंगे, और इसके बजाय सट्टेबाजों के माध्यम से जाएंगे। नहीं, निश्चित रूप से, हम दांव नहीं लगाते हैं, यह सब हमारे हित में है, अभिव्यक्ति का अर्थ है, उदाहरण के लिए, 4 से 1 मौका। सभी सट्टेबाजी खिलाड़ियों से परिचित बाधाओं "सफलताओं" का अनुपात "विफलताओं" हैं। प्रायिकताओं के संदर्भ में, संभावनाएँ एक घटना की संभावना होती हैं जो इस संभावना से विभाजित होती हैं कि घटना घटित नहीं होगी। हम किसी घटना के अवसर के लिए सूत्र लिखते हैं
(बाधाओं+) :
odds+= fracp+1−p+
जहाँ
p+ - किसी घटना के घटित होने की संभावना,
(1−पी+) - किसी घटना के न घटने की संभावना
उदाहरण के लिए, अगर एक युवा, मजबूत और उच्च-उत्साही घोड़े, उपनाम "वेटरोक" की संभावना है कि दौड़ में "मटिल्डा" नाम की बूढ़ी और भड़कीली बूढ़ी महिला को हराया जाएगा
0.8 , तो वेटरका की सफलता की संभावना होगी
4 को
1(0.8/(1−0.8)) और इसके विपरीत, अवसरों को जानना, हमारे लिए संभावना की गणना करना मुश्किल नहीं होगा
p+ :
fracp+1−p+=4 mkern15mu Longrightarrow mkern15mup+=4(1−p+) mkern15mu/Longrightarrow mkern15mu5p+=4 mkern15mu Longrightarrow mkern15mup+=0.8इस प्रकार, हम उन मूल्यों में संभावना का "अनुवाद" करना सीख गए हैं जो मान लेते हैं
0 को
+ infty । चलिए एक और कदम उठाते हैं और सीखते हैं कि पूरी संख्या रेखा से संभाव्यता का "अनुवाद" कैसे करें
− infty को
+ infty ।
चरण 2. हम संभाव्यता मानों को सीमा में अनुवाद करते हैं (− infty,+ infty)
यह कदम बहुत सरल है - हम यूलर संख्या के आधार पर बाधाओं का प्रस्ताव करते हैं
ई और:
f(w,xi)= vecwT vecx=ln(बाधाओं++)
अब हम जानते हैं कि यदि
p+=0.8 फिर मूल्य की गणना करें
च(w,xi) यह बहुत सरल होगा और इसके अलावा, यह सकारात्मक होना चाहिए:
f(w,xi)=ln(बाधाओं+)=ln(0.8/0.2)=ln(4) लगभग+1.38629 । तो यह है।
जिज्ञासा के लिए, हम जाँचते हैं कि यदि
p+=0.2 तब हम एक नकारात्मक मूल्य देखने की उम्मीद करते हैं
च(w,xi) । हम जाँच करते हैं:
f(w,xi)=ln(0.2/0.8)=ln(०.२५) लगभग−1.38629 । बिलकुल ठीक।
अब हम जानते हैं कि संभाव्यता मान का अनुवाद कैसे किया जाता है
0 को
1 से पूरी संख्या रेखा पर
− infty को
+ infty । अगले चरण में, हम इसके विपरीत करेंगे।
इस बीच, हम ध्यान दें कि लॉगरिथम के नियमों के अनुसार, फ़ंक्शन के मूल्य को जानना
च(w,xi) , आप बाधाओं की गणना कर सकते हैं:
odds+=ef(w,xi)=e vecwT vecx
अवसरों को निर्धारित करने का यह तरीका अगले चरण में काम आएगा।
चरण 3. हम निर्धारण के लिए एक सूत्र प्राप्त करते हैं p+
तो हमने सीखा, जानना
p+ फ़ंक्शन मान ढूंढें
च(w,xi) । हालांकि, वास्तव में, हमें इसके विपरीत - सब कुछ की आवश्यकता है - मूल्य जानना
च(w,xi) खोजने के लिए
p+ । ऐसा करने के लिए, हम इस तरह की अवधारणा को मौके के उलट कार्य के रूप में देखते हैं, जिसके अनुसार:
p+= fracodds+1+odds+
लेख में हम उपरोक्त सूत्र को प्राप्त नहीं करेंगे, लेकिन उपरोक्त उदाहरण से संख्याओं की जांच करेंगे। हम जानते हैं कि 4 से 1 की बाधाओं के साथ (
बाधाओं+=$ ), एक घटना होने की संभावना 0.8 है (
p+=0.8 )। चलो एक प्रतिस्थापन करें:
p+= frac41+4=0.8 । यह पहले की गई हमारी गणनाओं से मेल खाता है। हम आगे बढ़ते हैं।
अंतिम चरण में, हमने वह कटौती की
odds+=e vecwT vecx , जिसका मतलब है कि आप बाधाओं के उलटा कार्य में प्रतिस्थापन कर सकते हैं। हमें मिलता है:
p+= frace vecwT vecx1+e vecwT vecx
अंश और हर दोनों को विभाजित करके
e vecwT vecx तब:
p+= frac11+e− vecwT vecx= sigma( vecwT vecx)
प्रत्येक फायरमैन के लिए, यह सुनिश्चित करने के लिए कि हमने कहीं भी गलती नहीं की है, हम एक और छोटी जांच करेंगे। चरण 2 में, हम हैं
p+=0.8 निर्धारित किया है कि
f(w,xi) लगभग+1.38629 । फिर, मान का प्रतिस्थापन
च(w,xi) लॉजिस्टिक प्रतिक्रिया समारोह में, हम प्राप्त करने की उम्मीद करते हैं
p+=0.8 । स्थानापन्न और प्राप्त करें:
p+= frac11+e−1.38629=0.8बधाई हो, प्रिय पाठक, हमने अभी लॉजिस्टिक प्रतिक्रिया समारोह का विकास और परीक्षण किया है। आइए फ़ंक्शन ग्राफ को देखें।
चार्ट 3 "लॉजिस्टिक रिस्पांस फंक्शन"

साजिश रचने का कोड import math def logit (f): return 1/(1+math.exp(-f)) f = np.arange(-7,7,0.05) p = [] for i in f: p.append(logit(i)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$') plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16) plt.ylabel('$p_{i+}$', size = 16) plt.legend(prop = {'size': 14}) plt.show()
साहित्य में, आप इस फ़ंक्शन का नाम
सिग्मॉइड फ़ंक्शन के रूप में भी पा सकते हैं। ग्राफ स्पष्ट रूप से दिखाता है कि किसी वस्तु के किसी वर्ग से संबंधित होने की संभावना में मुख्य परिवर्तन अपेक्षाकृत छोटी सीमा में होता है
च(w,xi) कहीं से
−4 को
+4 ।
मैं अपने क्रेडिट विश्लेषक के पास लौटने और उसे ऋणों के पुनर्भुगतान की संभावना की गणना करने में मदद करने का प्रस्ताव रखता हूं, अन्यथा वह बोनस के बिना छोड़ दिए जाने का जोखिम चलाता है :)
तालिका 2 "संभावित उधारकर्ता"
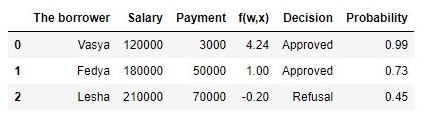
तालिका बनाने के लिए कोड proba = [] for i in df['f(w,x)']: proba.append(round(logit(i),2)) df['Probability'] = proba df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
इसलिए, हमने ऋण के पुनर्भुगतान की संभावना निर्धारित की। सब सब में, यह सच हो रहा है।
दरअसल, संभावना है कि 120,000 वेतन के साथ वास्या बैंक को मासिक रूप से 3.000 that का लाभ दे पाएगी। वैसे, हमें यह समझना चाहिए कि बैंक लेसा को एक ऋण भी दे सकता है यदि बैंक की नीति, उदाहरण के लिए, ऋण की चुकौती की संभावना से अधिक ग्राहकों को उधार देने के लिए कहती है, तो 0.3। बस इस मामले में, बैंक संभावित नुकसान के लिए एक बड़ा रिजर्व बनाएगा।
यह भी ध्यान दिया जाना चाहिए कि वेतन का अनुपात कम से कम 3 और 5.000 was के मार्जिन के साथ छत से लिया गया था। इसलिए, हम अपने मूल रूप में वेट वेक्टर का उपयोग नहीं कर सके
vecw=(−5000,1,−3) । हमें गुणांक को बहुत कम करने की आवश्यकता थी, और इस मामले में हमने प्रत्येक गुणांक को 25,000 से विभाजित किया, अर्थात वास्तव में, हमने परिणाम को समायोजित किया। लेकिन यह प्रारंभिक चरण में सामग्री की समझ को सरल बनाने के उद्देश्य से किया गया था। जीवन में, हमें गुणांक का आविष्कार और समायोजन करने की आवश्यकता नहीं है, लेकिन उन्हें खोजने के लिए। बस लेख के अगले खंडों में हम उन समीकरणों को प्राप्त करेंगे जिनके साथ मापदंडों का चयन किया गया है
vecw ।
04. वेट के वेक्टर को निर्धारित करने के लिए कम से कम वर्ग विधि vecw रसद प्रतिक्रिया समारोह में
हम पहले से ही एक वजन वेक्टर का चयन करने के लिए इस तरह की विधि जानते हैं
vecw कम से कम वर्ग विधि (ओएलएस) के रूप में और वास्तव में, हम बाइनरी वर्गीकरण समस्याओं में इसका उपयोग क्यों नहीं करते हैं? वास्तव में, कुछ भी
बहुराष्ट्रीय कंपनियों के उपयोग को रोकता है, केवल वर्गीकरण समस्याओं में यह विधि
लॉजिस्टिक लॉस की तुलना में कम सटीक परिणाम देती है। इसके लिए सैद्धांतिक औचित्य है। आइए एक सरल उदाहरण को देखें।
मान लीजिए कि हमारे मॉडल (
MSE और
लॉजिस्टिक लॉस का उपयोग करके) पहले से ही वेट वेक्टर का चयन शुरू कर चुके हैं
vecw और हमने कुछ कदम पर गणना रोक दी। इससे कोई फर्क नहीं पड़ता है, मध्य में, अंत में या शुरुआत में, मुख्य बात यह है कि हमारे पास पहले से ही वज़न और मान के वेक्टर के कुछ मूल्य हैं, इस कदम पर, वेट के वेक्टर
vecw दोनों मॉडलों के लिए कोई मतभेद नहीं है। फिर हम प्राप्त वज़न लेते हैं और उन्हें
लॉजिस्टिक रिस्पांस फ़ंक्शन में प्रतिस्थापित करते हैं (
frac11+e− vecwT vecx ) किसी वस्तु के लिए जो वर्ग से संबंधित है
+1 । हम दो मामलों की जांच करेंगे, जब वजन के चयनित वेक्टर के अनुसार, हमारे मॉडल में बहुत गलत है और इसके विपरीत - मॉडल दृढ़ता से आश्वस्त है कि ऑब्जेक्ट वर्ग से संबंधित है
+1 । आइए देखें कि
बहुराष्ट्रीय कंपनियों और
लॉजिस्टिक लॉस का उपयोग करते समय क्या जुर्माना "जारी" किया जाएगा।
उपयोग किए गए हानि फ़ंक्शन के आधार पर जुर्माना की गणना के लिए कोड स्थूल त्रुटि के साथ मामला - मॉडल ऑब्जेक्ट को वर्गीकृत करता है
+1 0.01 की संभावना के साथ
ओएलएस का उपयोग करते समय जुर्माना है:
MSE=(y−p+)=(1−0.01)2=0.9801लॉजिस्टिक लॉस का उपयोग करते समय जुर्माना है:
लॉगनुकसान=loge(1+e−yf(w,x))=loge(1+e−1(−4.595...)) लगभग4.605मजबूत निश्चितता वाला मामला - मॉडल ऑब्जेक्ट को वर्गीकृत करता है
+1 0.99 की संभावना के साथ
ओएलएस का उपयोग करते समय जुर्माना है:
MSE=(1−0.99)2=$0.000लॉजिस्टिक लॉस का उपयोग करते समय जुर्माना है:
लॉगनुकसान=loge(1+e−4.595...) लगभग0.01यह उदाहरण अच्छी तरह से दिखाता है कि सकल त्रुटि के साथ,
लॉग लॉस लॉस फ़ंक्शन मॉडल को
एमएसई से काफी अधिक जुर्माना करता है। आइए अब समझते हैं कि वर्गीकरण समस्याओं में
लॉग लॉस लॉस फ़ंक्शन का उपयोग करने के लिए सैद्धांतिक पूर्वापेक्षाएँ क्या हैं।
05. अधिकतम विश्वसनीयता विधि और लॉजिस्टिक प्रतिगमन
जैसा कि शुरुआत में वादा किया गया था, लेख सरल उदाहरण के साथ समाप्त हो गया। स्टूडियो में, एक और उदाहरण और पुराने मेहमान बैंक के उधारकर्ता हैं: वास्या, फेड्या और लेसा।
प्रत्येक फायरमैन के लिए, एक उदाहरण विकसित करने से पहले, मैं आपको याद दिला दूं कि जीवन में हम दसियों या सैकड़ों संकेतों के साथ हजारों या लाखों वस्तुओं के प्रशिक्षण नमूने के साथ काम कर रहे हैं। हालांकि, यहां संख्याओं को लिया जाता है ताकि वे एक नौसिखिए डेटास्टाइनस्ट के सिर में आसानी से फिट हो सकें।
हम उदाहरण के लिए लौटते हैं। कल्पना कीजिए कि बैंक के निदेशक ने उन सभी की जरूरत के लिए एक ऋण देने का फैसला किया, इस तथ्य के बावजूद कि एल्गोरिथ्म ने इसे लेसा को नहीं देने का सुझाव दिया था। और इतना समय बीत गया और हमें ज्ञात हो गया कि तीनों में से किस नायक ने ऋण चुकाया, और किसने नहीं। क्या उम्मीद की जानी चाहिए: वासा और फेड्या ने ऋण का भुगतान किया, लेकिन एलेक्स ने नहीं किया। अब कल्पना करते हैं कि यह परिणाम हमारे लिए एक नया प्रशिक्षण नमूना होगा और साथ ही, ऋण चुकौती (उधारकर्ता वेतन, मासिक भुगतान राशि) की संभावना को प्रभावित करने वाले कारकों के सभी डेटा गायब हो गए हैं। फिर, सहज रूप से, हम यह मान सकते हैं कि प्रत्येक तीसरा उधारकर्ता बैंक को ऋण वापस नहीं करता है, या दूसरे शब्दों में, अगले उधारकर्ता द्वारा ऋण वापस किए जाने की संभावना है
p= frac23 । इस सहज धारणा के लिए सैद्धांतिक प्रमाण हैं और यह
अधिकतम संभावना पद्धति पर आधारित है, जिसे अक्सर साहित्य में
अधिकतम संभावना सिद्धांत के रूप में संदर्भित किया जाता है।
सबसे पहले, वैचारिक तंत्र से परिचित हों।
एक
नमूने की संभावना केवल ऐसे नमूने प्राप्त करने की संभावना है, ठीक ऐसे अवलोकन / परिणाम प्राप्त करने की, अर्थात्। नमूने के परिणामों में से प्रत्येक को प्राप्त करने की संभावनाओं का उत्पाद (उदाहरण के लिए, एक ही समय में वास्या, फेडे और लेसा का ऋण चुकाया गया था या नहीं चुकाया गया था)।
संभावना फ़ंक्शन वितरण मापदंडों के मूल्यों के साथ एक नमूना की संभावना को जोड़ता है।
हमारे मामले में, प्रशिक्षण नमूना एक सामान्यीकृत बर्नौली योजना है जिसमें एक यादृच्छिक चर केवल दो मान लेता है:
1 या
0 । इसलिए, नमूने की संभावना को पैरामीटर की संभावना के एक फ़ंक्शन के रूप में लिखा जा सकता है
पी निम्नानुसार है:
P (\ mkern 5mu \ vec {y} \ mkern 5mu | \ mkern 5mu p) = \ prod \ limit_ {i = 1} ^ 3 p ^ {y_i} (1-p ^) {(1-y_i)} \ mkern 5mu = \ mkern 5mu p ^ 1 (1-p) ^ {1-1} \ centerdot p ^ 1 (1-p) ^ {1-1} \ centerdot p ^ 0 (1-p) ^ 1 -0} \ mkern 5mu == mkern5mup centerdotp centerdot(1−p) mkern5mu= mkern5mup2(1−p)उपरोक्त अभिलेख की व्याख्या निम्न प्रकार से की जा सकती है। वासिया और फेड्या द्वारा ऋण चुकाने की संयुक्त संभावना के बराबर है
p centerdotp=p2 इस बात की संभावना है कि एलेक्स ऋण नहीं चुकाएगा
1−पी (चूंकि यह ऋण का पुनर्भुगतान नहीं था), इसलिए, तीनों घटनाओं की संयुक्त संभावना है
p2(1−पी) ।
अधिकतम संभावना विधि एक अज्ञात पैरामीटर का आकलन करने की संभावना विधि को अधिकतम करके एक विधि है । हमारे मामले में, हमें इस तरह के मूल्य को खोजने की आवश्यकता हैp जिस पर P(→y|p)=p2(1−p)एक अधिकतम तक पहुँचता है।विचार कहाँ से आता है - एक अज्ञात पैरामीटर के मूल्य की तलाश करने के लिए जिस पर संभावना फ़ंक्शन अधिकतम तक पहुंच जाता है? इस विचार से उत्पत्ति की धारणा यह है कि नमूना केवल हमारे लिए उपलब्ध है, सामान्य आबादी के बारे में ज्ञान का स्रोत है। जो कुछ भी हम आबादी के बारे में जानते हैं वह नमूना में प्रस्तुत किया गया है। इसलिए, हम केवल इतना कह सकते हैं कि नमूना हमारे पास उपलब्ध जनसंख्या का सबसे सटीक प्रतिबिंब है। इसलिए, हमें एक पैरामीटर खोजने की आवश्यकता है जिसमें उपलब्ध नमूना सबसे अधिक संभावित हो जाता है।जाहिर है, हम एक अनुकूलन समस्या से निपट रहे हैं जिसमें किसी फ़ंक्शन के चरम बिंदु को खोजने की आवश्यकता होती है। चरम बिंदु को खोजने के लिए, पहले-क्रम की स्थिति पर विचार करना आवश्यक है, अर्थात् फ़ंक्शन के व्युत्पन्न को शून्य के बराबर करना और वांछित पैरामीटर के संबंध में समीकरण को हल करना। हालांकि, बड़ी संख्या में कारकों के एक उत्पाद के व्युत्पन्न की खोज लंबी हो सकती है, इसलिए इससे बचने के लिए एक विशेष तकनीक है - संभावना फ़ंक्शन के लॉगरिदम में संक्रमण । ऐसा संक्रमण क्यों संभव है? हम इस तथ्य पर ध्यान देते हैं कि हम फ़ंक्शन के चरम की तलाश में नहीं हैंP(→y|p) , और चरम बिंदु, अर्थात अज्ञात पैरामीटर का मान p जिस पर P(→y|p)एक अधिकतम तक पहुँचता है। लॉगरिदम में संक्रमण होने पर, चरम बिंदु नहीं बदलता (हालांकि एक्सट्रीम स्वयं अलग होगा), क्योंकि लॉगरिथम एक मोनोटोनिक फ़ंक्शन है।आइए, पूर्वगामी के अनुसार, वास, फेडी और लेसा के साथ ऋण के हमारे उदाहरण को विकसित करना जारी रखें। सबसे पहले, आइए संभावना फ़ंक्शन के लघुगणक पर चलते हैं :logP(→y|p)=logp2(1−p)=2logp+log(1−p)अब हम किसी अभिव्यक्ति को आसानी से अलग कर सकते हैं p :∂logP(→y|p)∂p=∂∂p(2logp+log(1−p))=2p−11−pऔर अंत में, पहले क्रम की स्थिति पर विचार करें - हम फ़ंक्शन के व्युत्पन्न को शून्य के बराबर करते हैं:2p−11−p=0⟹2p=11−p⟹2(1−p)=p⟹p=23इस प्रकार, ऋण चुकौती की संभावना का हमारा सहज मूल्यांकन p=23सैद्धांतिक रूप से पुष्ट किया गया था।महान, लेकिन अब हम इस जानकारी के साथ क्या करते हैं? अगर हम यह मान लें कि हर तीसरा कर्जदार बैंक को पैसा नहीं लौटाता है, तो बाद वाला अनिवार्य रूप से दिवालिया हो जाएगा। और इसलिए यह है, लेकिन केवल जब ऋण के पुनर्भुगतान की संभावना का बराबर मूल्यांकन23हमने ऋण की चुकौती को प्रभावित करने वाले कारकों को ध्यान में नहीं रखा: उधारकर्ता का वेतन और मासिक भुगतान राशि। याद रखें कि पहले हमने प्रत्येक ग्राहक द्वारा ऋण चुकौती की संभावना की गणना की थी, इन बहुत कारकों को ध्यान में रखते हुए। यह तार्किक है कि हमें जो संभावनाएँ मिलीं, वे बराबर के बराबर से भिन्न हैं23 ।
चलो नमूनों की संभावना निर्धारित करते हैं:नमूनों की संभावना की गणना के लिए कोड from functools import reduce def likelihood(y,p): line_true_proba = [] for i in range(len(y)): ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i]) line_true_proba.append(ltp_i) likelihood = [] return reduce(lambda a, b: a*b, line_true_proba) y = [1.0,1.0,0.0] p_log_response = df['Probability'] const = 2.0/3.0 p_const = [const, const, const] print ' p=2/3:', round(likelihood(y,p_const),3) print '****************************************************************************************************' print ' p:', round(likelihood(y,p_log_response),3)
एक निरंतर मूल्य पर नमूने की संभावना p=23 :P(→y|p)=p2(1−p)=232(1−23)≈0.148खाते के कारकों में ऋण चुकौती की संभावना की गणना में नमूना लेने की संभावना →x :P(→y|p)=3∏i=1pyi(1−p)(1−yi)=p11(1−p1)1−1⋅p12(1−p2)1−1⋅p03(1−p3)1−0==p1⋅p2⋅(1−p3)=0.99⋅0.73⋅(1−0.45)≈0.397कारकों के आधार पर गणना की जाने वाली संभाव्यता के साथ नमूने की संभावना संभावना के निरंतर मूल्य के साथ संभावना से अधिक थी। ये कैसी बात कर रहा है? इससे पता चलता है कि कारकों के ज्ञान ने प्रत्येक ग्राहक के लिए ऋण चुकौती की संभावना का अधिक सटीक रूप से चयन करना संभव बना दिया है। इसलिए, जब कोई अन्य ऋण जारी करता है, तो लेख के तीसरे खंड के अंत में प्रस्तावित ऋण चुकौती की संभावना का आकलन करने के लिए मॉडल का उपयोग करना अधिक सही होगा।लेकिन फिर, अगर हमें नमूने के कार्य को अधिकतम करने की आवश्यकता है, तो फिर कुछ एल्गोरिथ्म का उपयोग क्यों न करें, जो क्रमशः वास्या, फेडी और लेशा के लिए संभाव्यताएं देगा, उदाहरण के लिए, क्रमशः 0.99, 0.99 और 0.01 के बराबर। शायद ऐसा एल्गोरिथ्म प्रशिक्षण नमूने में खुद को अच्छी तरह से दिखाएगा, क्योंकि यह नमूने की संभावना के मूल्य को करीब लाएगा1, लेकिन, सबसे पहले, इस तरह के एल्गोरिथ्म में सबसे अधिक संभावना सामान्यीकरण क्षमता के साथ कठिनाइयां होंगी, और दूसरी बात, यह एल्गोरिथ्म निश्चित रूप से रैखिक नहीं होगा। और अगर इस लेख की योजना में रिट्रेनिंग (समान रूप से कमजोर सामान्यीकरण क्षमता) से निपटने के तरीके स्पष्ट रूप से शामिल नहीं हैं, तो आइए अधिक विस्तार से दूसरे पैराग्राफ पर जाएं। ऐसा करने के लिए, बस एक सरल प्रश्न का उत्तर दें। क्या हमारे द्वारा ज्ञात कारकों को ध्यान में रखते हुए, वासा और फेडे को ऋण चुकाने की संभावना समान हो सकती है? ध्वनि तर्क की दृष्टि से, निश्चित रूप से, यह नहीं हो सकता। इसलिए, वासा अपने वेतन का 2.5% प्रति माह ऋण चुकाने के लिए देगा, और फेड्या - लगभग 27.8%। इसके अलावा ग्राफ 2 "ग्राहकों का वर्गीकरण" हम देखते हैं कि वास्या फेडिया की तुलना में वर्गों को अलग करने वाली रेखा से बहुत आगे है। और अंत में, हम जानते हैं कि फ़ंक्शनf(w,x)=w0+w1x1+w2x2वास्या और फेडी के लिए इसके अलग-अलग अर्थ हैं: वास्या के लिए 4.24 और फेडी के लिए 1.0। अब, यदि उदाहरण के लिए, फेडिया ने अधिक परिमाण का आदेश अर्जित किया या छोटे ऋण के लिए कहा, तो वास और फेडी से ऋण का भुगतान करने की संभावनाएं समान होंगी। दूसरे शब्दों में, एक रैखिक संबंध को मूर्ख नहीं बनाया जा सकता है। और अगर हम वास्तव में बाधाओं की गणना करते हैंw , लेकिन वे उन्हें छत से नहीं ले गए, हम सुरक्षित रूप से हमारे मूल्यों की घोषणा कर सकते थे w आपको प्रत्येक उधारकर्ता द्वारा ऋण की चुकौती की संभावना का आकलन करने की अनुमति देता है, लेकिन चूंकि हम इस बात पर विचार करने के लिए सहमत हैं कि गुणांक का निर्धारण wसभी नियमों के अनुसार किया गया था, तब हम इस पर विचार करेंगे - हमारे गुणांक हमें संभावना का बेहतर अनुमान देने की अनुमति देते हैं :)हालांकि, हम विचलित थे। इस खंड में, हमें यह समझने की आवश्यकता है कि वजन के वेक्टर का निर्धारण कैसे किया जाता है→w, जो प्रत्येक उधारकर्ता द्वारा ऋण वापसी की संभावना का आकलन करने के लिए आवश्यक है।संक्षेप में संक्षेप में बताएं कि हम किस शस्त्रागार की तलाश कर रहे हैंw:1. हम मानते हैं कि लक्ष्य चर (पूर्वानुमान मूल्य) और परिणाम को प्रभावित करने वाले कारक के बीच संबंध रैखिक है। इस कारण से, प्रपत्र के रैखिक प्रतिगमन फ़ंक्शन का उपयोग किया जाता है।f(w,x)=→wTX जिनकी रेखा वस्तुओं (क्लाइंट) को कक्षाओं में विभाजित करती है +1 और −1 या 0(ग्राहक जो ऋण चुकाने में सक्षम हैं और सक्षम नहीं हैं)। हमारे मामले में, समीकरण का रूप हैf(w,x)=w0+w1x1+w2x2 ।
2. हम फॉर्म के व्युत्क्रम लॉग ट्रांसफ़ॉर्मेशन फ़ंक्शन का उपयोग करते हैंp+=11+e−→wT→x=σ(→wT→x) इस संभावना को निर्धारित करने के लिए कि कोई वस्तु किसी वर्ग की है +1 ।
3. हम अपने प्रशिक्षण नमूने को एक सामान्यीकृत बर्नौली योजना के कार्यान्वयन के रूप में मानते हैं , अर्थात, प्रत्येक वस्तु के लिए एक यादृच्छिक चर उत्पन्न होता है, जो कि संभाव्यता के साथ होता है।p (प्रत्येक वस्तु के लिए अपने स्वयं के) मान 1 और संभावना के साथ लेता है (1–p)- 0.4. हम जानते हैं कि हमें नमूना के संभावित कार्य को अधिकतम करने की आवश्यकता है , स्वीकार किए गए कारकों को ध्यान में रखते हुए, ताकि मौजूदा नमूना सबसे अधिक संभावना बन जाए। दूसरे शब्दों में, हमें ऐसे मापदंडों का चयन करने की आवश्यकता है, जिस पर नमूना सबसे अधिक प्रशंसनीय होगा। हमारे मामले में, चयनित पैरामीटर ऋण के पुनर्भुगतान की संभावना हैp , जो बदले में अज्ञात गुणांक पर निर्भर करता है w ।
तो हम वजन के इस तरह के एक वेक्टर खोजने की जरूरत है →wजिस पर नमूने की संभावना अधिकतम होगी।5. हम जानते हैं कि एक नमूना की संभावना समारोह को अधिकतम करने के लिए , आप अधिकतम संभावना विधि का उपयोग कर सकते हैं । और हम इस विधि के साथ काम करने के सभी गुर जानते हैं।यहाँ इस तरह के एक बहु-मार्ग है :)और अब याद करते हैं कि लेख की शुरुआत में हम दो प्रकार के लॉजिस्टिक लॉस लॉस फ़ंक्शन को प्राप्त करना चाहते थे , यह इस बात पर निर्भर करता है कि वस्तुओं के वर्ग कैसे नामित किए जाते हैं। ऐसा हुआ कि दो वर्गों के साथ वर्गीकरण समस्याओं में, कक्षाओं को निरूपित किया जाता है+1 और 0 या −1 ।
पदनाम के आधार पर, आउटपुट में एक समान हानि फ़ंक्शन होगा।केस 1. वस्तुओं का वर्गीकरण +1 और 0
इससे पहले, एक नमूने की संभावना का निर्धारण करने में जिसमें उधारकर्ता द्वारा ऋण की चुकौती की संभावना कारकों और निर्दिष्ट गुणांक के आधार पर गणना की गई थी। w , हमने सूत्र लागू किया:P(→y|p)=3∏i=1pyi(1−p)(1−yi)वास्तव में piलॉजिस्टिक प्रतिक्रिया समारोह का मूल्य है p+=11+e−→wT→x=σ(→wT→x) किसी दिए गए वेट वेक्टर के लिए →wफिर कुछ भी हमें इस तरह से नमूने के संभावित कार्य को लिखने से रोकता है:P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)yi(1−σ(→wT→xi)(1−yi)→max
ऐसा होता है कि कभी-कभी, कुछ नौसिखिए विश्लेषकों के लिए, यह समझना मुश्किल है कि यह फ़ंक्शन कैसे काम करता है। आइए 4 छोटे उदाहरण देखें जो सब कुछ स्पष्ट करेंगे:1. यदिyi=+1 (यानी, प्रशिक्षण के नमूने के अनुसार, ऑब्जेक्ट कक्षा +1 का है), और हमारा एल्गोरिथ्म σ(→wTX)) किसी वस्तु को वर्गीकृत करने की संभावना को निर्धारित करता है +1 0.9 के बराबर है, तो नमूने की संभावना के इस टुकड़े की गणना निम्नानुसार की जाएगी:0.91⋅(1−0.9)(1−1)=0.91⋅0.10=0.92. यदिyi=+1 , और σ(→wTX))=0.1 , तो गणना इस तरह होगी:0.11⋅(1−0.1)(1−1)=0.11⋅0.90=0.13. अगरyi=0 , और σ(→wTX))=0.1 , तो गणना इस तरह होगी:0.10⋅(1−0.1)(1−0)=0.10⋅0.91=0.94. यदिyi=0 , और σ(→wTX))=0.9 , तो गणना इस तरह होगी:0.90⋅(1−0.9)(1−0)=0.90⋅0.11=0.1जाहिर है, संभावना समारोह 1 और 3 के मामलों में अधिकतम किया जाएगा, या सामान्य मामले में, एक वर्ग के रूप में एक वस्तु को वर्गीकृत करने की संभावनाओं का सही अनुमान लगाया मूल्यों के साथ +1 ।
इस तथ्य के कारण कि किसी वस्तु को कक्षा के रूप में वर्गीकृत करने की संभावना का निर्धारण करते समय +1 हम केवल गुणांक नहीं जानते हैं w, तब हम उनकी तलाश करेंगे। जैसा कि ऊपर उल्लेख किया गया है, यह एक अनुकूलन समस्या है जिसमें हमें सबसे पहले वेट वेक्टर के संबंध में संभावना फ़ंक्शन के व्युत्पन्न को खोजने की आवश्यकता हैw ।
हालांकि, पहले कार्य को सरल बनाने के लिए समझ में आता है: हम संभावना फ़ंक्शन के लघुगणक के व्युत्पन्न की तलाश करेंगे ।Llog(X,→y,→w)=n∑i=1(−yilogeσ(→wT→xi)−(1−yi)loge(1−σ(→wT→xi)))→min
लॉगरिदम के बाद, लॉजिस्टिक एरर के फंक्शन में , हमने साइन इन को बदल दिया+ पर − ।
सब कुछ सरल है, क्योंकि यह मॉडल गुणवत्ता मूल्यांकन की समस्याओं में एक फ़ंक्शन के मूल्य को कम करने के लिए प्रथागत है, हमने अभिव्यक्ति के दाईं ओर को गुणा किया है −और तदनुसार अधिकतम करने के बजाय, अब हम फ़ंक्शन को कम करते हैं।दरअसल, अब, आपकी आंखों के सामने, नुकसान का कार्य - दो वर्गों के साथ प्रशिक्षण सेट के लिए लॉजिस्टिक नुकसान का सामना करना पड़ा ।+1 और 0 ।
अब, गुणांक खोजने के लिए, हमें बस लॉजिस्टिक एरर फंक्शन के व्युत्पन्न को खोजने की जरूरत है और फिर, न्यूमेरिकल ऑप्टिमाइज़ेशन मेथड्स, जैसे कि ग्रेडिएंट डिसेंट या स्टोचैस्टिक ग्रेडिएंट डिसेंट का उपयोग करते हुए, सबसे इष्टतम एफिशिएंसी का चयन करें।w ।
लेकिन, लेख के पहले से ही छोटे आकार को देखते हुए, इसे स्वतंत्र रूप से अंतर करने का प्रस्ताव है या, शायद, यह अगले लेख के लिए इस तरह के विस्तृत उदाहरणों के बिना बहुत सारे अंकगणित के साथ विषय होगा।केस 2. वस्तुओं का वर्गीकरण +1 और −1
यहां का दृष्टिकोण कक्षाओं के समान ही होगा 1 और 0लेकिन लॉजिस्टिक लॉस लॉस फ़ंक्शन के आउटपुट के लिए रास्ता अधिक अलंकृत होगा। नीचे उतरना। संभावना समारोह के लिए, हम "यदि ... तो ..." ऑपरेटर का उपयोग करते हैं । वह है, अगरi वें ऑब्जेक्ट क्लास का है +1 , तो नमूने की संभावना की गणना करने के लिए, हम संभावना का उपयोग करते हैं p यदि वस्तु वर्ग की है −1 , फिर सत्यनिष्ठा विकल्प में (1−p) ।
यह संभावना समारोह की तरह दिखता है:P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)[yi=+1](1−σ(→wT→xi)[yi=−1])→max
हम उंगलियों पर लिखते हैं कि यह कैसे काम करता है। 4 मामलों पर विचार करें:1. यदिyi=+1 और σ(→wT→xi)=0.9 , तो नमूना "जाओ" के सत्यापन में 0.92. यदिyi=+1 और σ(→wT→xi)=0.1 , तो नमूना "जाओ" के सत्यापन में 0.13. अगरyi=−1 और σ(→wT→xi)=0.1 , तो नमूना "जाओ" के सत्यापन में 1−0.1=0.94. यदिyi=−1 और σ(→wT→xi)=0.9 , तो नमूना "जाओ" के सत्यापन में 1−0.9=0.1जाहिर है, मामलों में 1 और 3, जब एल्गोरिदम द्वारा संभावनाओं को सही ढंग से निर्धारित किया गया था, तो संभावना फ़ंक्शन को अधिकतम किया जाएगा, यही वह है जो हम प्राप्त करना चाहते थे। हालांकि, यह दृष्टिकोण बल्कि बोझिल है, और हम नीचे एक अधिक कॉम्पैक्ट रिकॉर्डिंग पर विचार करेंगे। लेकिन पहले, संकेत के परिवर्तन के साथ संभावना समारोह का लघुगणक, क्योंकि अब हम इसे कम कर देंगे।Llog(X,→y,→w)=n∑i=1(−[yi=+1]logeσ(→wT→xi)−[yi=−1]loge(1−σ(→wT→xi)))→min
इसके बजाय स्थानापन्न σ(→wT→xi) अभिव्यक्ति 11+e−→wT→xi :Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(1−11+e−→wT→xi))→min
सरल अंकगणितीय तकनीकों का उपयोग करके लघुगणक के तहत सही शब्द को सरल बनाएं और प्राप्त करें:Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(11+e→wT→xi))→min
और अब ऑपरेटर से छुटकारा पाने का समय है "अगर ... फिर ..." । ध्यान दें कि जब कोई वस्तुyi वर्ग के अंतर्गत आता है +1 , तब, लघुगणक के अंतर्गत, अभिव्यक्ति में, e सत्ता के लिए उठाया −→wT→xi यदि वस्तु वर्ग की है −1 तब $ e $ को एक शक्ति के लिए उठाया जाता है +→wT→xi ।
इसलिए, दोनों मामलों को एक में मिलाकर एक डिग्री लिखना सरल किया जा सकता है: −yi→wT→xi ।
तब लॉजिस्टिक एरर फंक्शन फॉर्म लेता है:Llog(X,→y,→w)=n∑i=1−loge(11+e−yi→wT→xi)→min
लघुगणक के नियमों के अनुसार, अंश को पलटें और चिह्न निकालें " − "(ऋण) प्रति लघुगणक, हम प्राप्त करते हैं:Llog(X,→y,→w)=n∑i=1loge(1+e−yi→wT→xi)→min
यहां हानि फ़ंक्शन लॉजिस्टिक लॉस है , जिसका उपयोग कक्षाओं से संबंधित वस्तुओं के साथ प्रशिक्षण सेट में किया जाता है:+1 और −1 ।
खैर, इस बिंदु पर मैं अपनी छुट्टी लेता हूं और हम लेख को समाप्त करते हैं।← लेखक का पिछला काम - "हम रैखिक प्रतिगमन समीकरण को मैट्रिक्स रूप में लाते हैं"सहायक सामग्री
1. साहित्य
1) एप्लाइड प्रतिगमन विश्लेषण / एन। ड्रेपर, जी। स्मिथ - 2 एड। - एम .: वित्त और सांख्यिकी, 1986 (अंग्रेजी से अनुवादित)2) संभाव्यता सिद्धांत और गणितीय सांख्यिकी / वी.ई. Gururman - 9 वां संस्करण। - एम .: हायर स्कूल, 20033) प्रायिकता सिद्धांत / एन.आई. चेरनोवा - नोवोसिबिर्स्क: नोवोसिबिर्स्क स्टेट यूनिवर्सिटी, 20074) बिजनेस एनालिटिक्स: डेटा से ज्ञान तक / पाक्लिन एन। बी।, ओरेश्कोव वी। आई। - द्वितीय संस्करण। - सेंट पीटर्सबर्ग: पीटर, 20135) स्क्रैच / जोएल ग्रास से डेटा साइंस डेटा साइंस - सेंट पीटर्सबर्ग: बीएचवी पीटर्सबर्ग, 20176) डेटा साइंस विशेषज्ञों के लिए व्यावहारिक आंकड़े / पी। ब्रूस, ई। ब्रूस - सेंट पीटर्सबर्ग: BHV पीटर्सबर्ग, 20182. व्याख्यान, पाठ्यक्रम (वीडियो)
1) अधिकतम संभावना विधि का सार, बोरिस डेमेशेव2) निरंतर मामले में अधिकतम संभावना विधि, बोरिस डेमेशेव3) लॉजिस्टिक प्रतिगमन। ओपन कोर्स ओडीएस, यूरी कश्नीत्स्की4) लेक्चर 4, एवगेनी सोकोलोव (47 मिनट के वीडियो के साथ)5) लॉजिस्टिक रिग्रेशन, व्याचेस्लाव व्रोनटोव3. इंटरनेट के स्रोत
1) वर्गीकरण और प्रतिगमन के रैखिक मॉडल2) लॉजिस्टिक रिग्रेशन को समझना आसान है3) लॉजिस्टिक फ़ंक्शन ऑफ़ एरर4) इंडिपेंडेंट टेस्ट और बर्नौली फॉर्मूला5) आईएमएफ का बैलेड6) अधिकतम संभावना विधि7) लॉगरिदम के सूत्र और गुण8) संख्या क्यों है e ?9) रैखिक क्लासिफायरियर