Batang Zhenya dan Luke - alat pengganda dari akhir abad XIX
Artikel ini dikhususkan untuk alat bantu untuk perkalian, bar yang diusulkan pada tahun 1885 oleh insinyur kereta api Eugene (sic) dan seorang karyawan Museum Seni dan Kerajinan Paris Eduard Luke (sic) [1].Transliterasi nama-nama penemu berbeda dalam sumber yang berbeda, jadi saya mengutip dalam bahasa Latin sejumlah opsi (yang harus saya google): Genaille (Zhenya, Zhenya, Zhenya, Zhenya, Zhenail), Lucas (Luca, Luc, Lucas).Batang-batang Zhenya dan Luke lebih nyaman daripada tongkat Neper yang mendahuluinya, dan bisa bersaing dengan batang-batang modern Joffe (dibangun di atas teorema Slonimsky).Praktis tidak ada informasi tentang produk ini di Runet. Suatu hari, saya tiba-tiba mencari artikel di Jerman yang membantu saya memahami prinsip bar. Tidak terbatas pada artikel, saya mengembalikan penampilan permukaan kerja dari gambar dengan pandangan beberapa dari mereka dan fokus pada prinsip aksi mereka. Bahan-bahan yang ditemukan kemudian di situs yang sama mengkonfirmasi kebenaran rekonstruksi saya.Tujuan penulisan artikel
Artikel ini ditujukan bagi mereka yang, seperti saya, tertarik pada sejarah teknologi komputer.Di RuNet, saya tidak dapat menemukan apa pun yang masuk akal tentang jeruji Zhenai dan Luc (Genaille & Lucas). Situs web berbahasa Jerman , tempat artikel dengan uraiannya ditemukan, membantu memahami prinsip pengoperasian alat hitung ini .Mengapa Habr dipilih sebagai penempatan artikel
Artikel ini dikhususkan, meskipun kuno, tetapi masih menggunakan teknologi komputasi. Karena itu, cocok untuk Habr pada suatu subjek.Habr diindeks dengan baik, dan saya ingin mudah bagi siapa saja yang tertarik dengan alat penghitungan ini untuk menemukan informasi tentang itu.Deskripsi dan Fungsi Produk
Batang Zhenya dan Luke, serta produk serupa lainnya, dirancang untuk dengan cepat mendapatkan produk dari nomor multi-digit dengan nomor satu digit.Alat pengganda adalah satu set 11 batang. Setiap bilah memiliki skala digital di mana hasilnya berada. Skala ini dibagi menjadi 8 bagian, yang sesuai dengan perkalian dengan angka dari 2 hingga 9. Satu batang berfungsi sebagai petunjuk - bagian-bagian dari skalanya ditandatangani oleh angka 2 ... 9 - ini adalah nilai-nilai faktor satu digit, dan skalanya sendiri dirancang untuk membaca tingkat pekerjaan tertinggi. Bilah yang tersisa diberi nomor dari 0 hingga 9 dan dirancang untuk melipatgandakan angka yang sesuai. Di dalamnya, di sebelah skala, ada segitiga, sisi kanan yang membatasi skala digital ke kiri, dan verteks kiri berada di tepi kiri bar - ketika bar ditumpuk bersama-sama, ini menunjukkan posisi pelepasan produk berikutnya pada bar berikutnya.









 Analisis kecil: mudah untuk melihat bahwa setiap bagian dari skala masing-masing batang dimulai dengan angka yang sama dengan nilai kategori unit produk dari jumlah batang dengan nomor bagian skala. Misalnya, pada bilah 8, fragmen 9 dimulai dengan angka 2 (8 * 9 = 72). Panjang setiap bagian skala sama dengan nilai faktor satu digit - yang alami, karena ketika mengalikan angka apa pun dengan faktor satu digit, angka tertinggi produk kurang dari faktor ini, mis. ketika dikalikan, misalnya, dengan 5, nilai yang ditransfer ke digit berikutnya tidak akan pernah melebihi 4, ketika dikalikan dengan 9, masing-masing, 8, dll. Jumlah pergeseran digit ke bawah dari awal skala sama dengan nilai transfer dari bit paling signifikan. Ternyata posisi verteks kiri dari segitiga hitam sesuai dengan nilai bit kedua dari produk nomor bar dengan faktor satu digit, yang ditambahkan nomor,ditransfer dari pesanan rendah.Untuk mengalikan angka multi-digit dengan yang satu digit, tambahkan bilah bersama-sama dengan angka yang sesuai dengan digit digit dan pasang bilah dengan petunjuk di sebelah kiri. Kemudian di setiap bagian skala akan dimungkinkan untuk mempertimbangkan produk dari nomor ini dengan nomor satu digit yang sesuai. Pelepasan unit adalah digit pertama dari bagian skala yang diinginkan, dan setiap pelepasan berikutnya akan menunjukkan kepada kita titik kiri segitiga, sisi kanan yang berfungsi sebagai perbatasan kiri sel dari pelepasan sebelumnya.Sebagai contoh, ambil angka 7519. Mari kita mengumpulkan bar dengan petunjuk dan bar 7, 5, 1, dan 9. Diagram ditunjukkan pada gambar di bawah ini.
Analisis kecil: mudah untuk melihat bahwa setiap bagian dari skala masing-masing batang dimulai dengan angka yang sama dengan nilai kategori unit produk dari jumlah batang dengan nomor bagian skala. Misalnya, pada bilah 8, fragmen 9 dimulai dengan angka 2 (8 * 9 = 72). Panjang setiap bagian skala sama dengan nilai faktor satu digit - yang alami, karena ketika mengalikan angka apa pun dengan faktor satu digit, angka tertinggi produk kurang dari faktor ini, mis. ketika dikalikan, misalnya, dengan 5, nilai yang ditransfer ke digit berikutnya tidak akan pernah melebihi 4, ketika dikalikan dengan 9, masing-masing, 8, dll. Jumlah pergeseran digit ke bawah dari awal skala sama dengan nilai transfer dari bit paling signifikan. Ternyata posisi verteks kiri dari segitiga hitam sesuai dengan nilai bit kedua dari produk nomor bar dengan faktor satu digit, yang ditambahkan nomor,ditransfer dari pesanan rendah.Untuk mengalikan angka multi-digit dengan yang satu digit, tambahkan bilah bersama-sama dengan angka yang sesuai dengan digit digit dan pasang bilah dengan petunjuk di sebelah kiri. Kemudian di setiap bagian skala akan dimungkinkan untuk mempertimbangkan produk dari nomor ini dengan nomor satu digit yang sesuai. Pelepasan unit adalah digit pertama dari bagian skala yang diinginkan, dan setiap pelepasan berikutnya akan menunjukkan kepada kita titik kiri segitiga, sisi kanan yang berfungsi sebagai perbatasan kiri sel dari pelepasan sebelumnya.Sebagai contoh, ambil angka 7519. Mari kita mengumpulkan bar dengan petunjuk dan bar 7, 5, 1, dan 9. Diagram ditunjukkan pada gambar di bawah ini.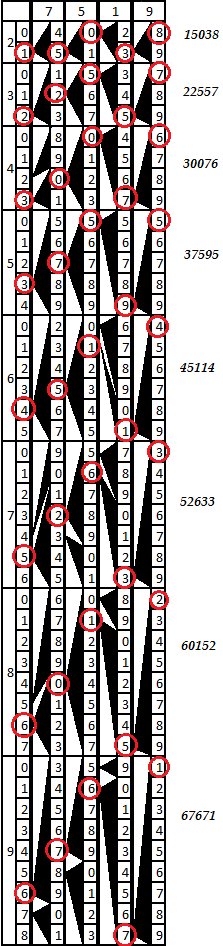 Di setiap bagian dari tabel yang dihasilkan, mengikuti tanda-tanda segitiga, Anda dapat melacak kategori karya dari kanan ke kiri.Skema ini lebih jelas daripada kata-kata apa pun. Mari kita ikuti, misalnya, perkalian dengan 9. Pada awal bagian kesembilan (terakhir) dari skala bar kanan kita melihat angka 1. Segitiga darinya menunjukkan angka 7 dari bar tetangga, dari sana segitiga menunjukkan 6, lalu - 7, dan lebih jauh lagi - angka 6 pada skala bar-tip. UNTUK. kami mendapatkan nilai 67671 = 7519 * 9.Karya-karya lain juga dilacak. Sangat mudah untuk memverifikasi bahwa mereka benar. Karena itu, alat ini cocok untuk digunakan.
Di setiap bagian dari tabel yang dihasilkan, mengikuti tanda-tanda segitiga, Anda dapat melacak kategori karya dari kanan ke kiri.Skema ini lebih jelas daripada kata-kata apa pun. Mari kita ikuti, misalnya, perkalian dengan 9. Pada awal bagian kesembilan (terakhir) dari skala bar kanan kita melihat angka 1. Segitiga darinya menunjukkan angka 7 dari bar tetangga, dari sana segitiga menunjukkan 6, lalu - 7, dan lebih jauh lagi - angka 6 pada skala bar-tip. UNTUK. kami mendapatkan nilai 67671 = 7519 * 9.Karya-karya lain juga dilacak. Sangat mudah untuk memverifikasi bahwa mereka benar. Karena itu, alat ini cocok untuk digunakan.Spekulasi tentang tema penampilan
Apokin I.A., Maistrov L.E. dalam sumber [1] mereka menulis bahwa bilah digital memiliki keempat permukaan yang berfungsi. Adalah logis untuk mengasumsikan bahwa permukaan digunakan untuk menduplikasi skala, yang diperlukan untuk mengkompilasi angka multi-digit dengan beberapa kemunculan dari digit yang sama.Berdasarkan jumlah sisi bar, misalkan ada empat set timbangan lengkap pada 10 bar.Misalkan skala pada bar harus diatur sehingga bar memungkinkan Anda untuk membuat angka empat digit.Anda dapat menemukan banyak opsi untuk menempatkan skala kerja di bar yang memenuhi persyaratan ini. Misalnya, ambil dua batang dari lima jenis yang memiliki wajah, masing-masing:0,1,2,3;2,3,4,5;4,5,6,7;6,7,8,9;0,1,8,9.Pilihan lain untuk menggunakan empat wajah adalah menempatkan satu skala pada mereka di bagian-bagian dan dengan demikian mengurangi panjang bar. Opsi ini kurang nyaman digunakan, karena tidak memungkinkan untuk melihat semua karya sekaligus.Skala ini terdiri dari 8 bagian, dengan panjang mulai dari 2 hingga 9. Kumpulkan mereka menjadi empat kelompok tanpa mengganggu urutan:2 + 3 + 4 + 5 = 14; 6 + 7 = 13; 8; 9. Panjang terpanjang adalah 14.Jika diizinkan mengganggu pesanan, maka bagian skala mudah dikelompokkan:2 + 9; 3 + 8; 4 + 7; 6 + 5. Itu panjang batang dikurangi menjadi 11.literatur
1. Apokin I.A., Maistrov L.E. "Sejarah teknologi komputer: Dari perangkat komputasi yang paling sederhana hingga sistem relay yang kompleks." (Moskow: Nauka Publishing House, 1990)2. www.mechrech.infoPS
Sebuah pertanyaan bagi mereka yang tahu bahasa Prancis: bagaimana bisa menerjemahkan nama Genaille dan Lucas dengan benar?UPD: Terima kasih. Diperbaiki di seluruh artikel tentang Zhenai (kelas) dan Luke (non-kelas) Source: https://habr.com/ru/post/id380549/
All Articles