Geekly articles weekly

Catatan Kalibrasi Sensor Posisi Rumah

Beberapa sensor akselerasi memerlukan kalibrasi nol tambahan setelah pemasangan di papan. Ketika saya melihat beberapa sumber dengan kalibrasi sensor akselerasi, di mana komponen G diperhitungkan hanya dengan mengurangi nilai = 9,8 m / s2 dari sumbu Z, muncul ide untuk menulis catatan ini.




Struktur publikasi


  • Masalah
  • Pernyataan masalah dan metode solusi
  • Bagaimana cara mendapatkan poin?
  • Bagaimana cara menghitung bagian tengah bola?
  • Bagaimana cara mempercepat pencarian pusat bola?
  • Bagaimana lagi untuk mempercepat pencarian pusat bola?
  • Tentang kesalahan pengukuran
  • Total


Masalah


Apa masalahnya - Sensor MEMS setelah pemasangan di papan mengalami deformasi kecil yang memengaruhi:
  • posisi nol;
  • penskalaan nilai yang diukur;
  • tegak lurus sumbu satu sama lain.

Dan jika scaling dan tegak lurus dilanggar tidak begitu terasa, maka posisi nol akan kusut secara nyata. Misalnya, jika Anda menerjemahkan nilai khas dari offset nol untuk accelerometer sensor MPU9250 menjadi m / s 2 , maka ini diperoleh di wilayah 0,2 m / s 2 . Artinya, sensornya diam, tetapi menunjukkan akselerasi, dan setelah 5 detik kita mendapatkan kecepatan 1 m / s. Di satu sisi, semua data sensor selalu melewati beberapa jenis filter (misalnya, seperti itu ). Tetapi di sisi lain, mengapa filter harus secara konstan mengimbangi bias ini? Setelah semua, sensor akan menunjukkan gerakan di tempat yang tidak. Ini mengurangi akurasi hasil. Secara keseluruhan, Anda perlu menemukan nilai offset sekali dan kemudian kurangi nilai ini dari pembacaannya selama operasi sensor.

Solusi paling sederhana untuk menemukan nilai zero offset, yang langsung muncul di benak, adalah menciptakan kondisi di mana sensor harus secara akurat menunjukkan nol. Nilai yang terekam pada sensor adalah nilai zero offset! Begitu? Tapi tidak - gravitasi terus bekerja pada accelerometer. Untuk menghindarinya, bobot akan dibutuhkan (melempar tidak akan berhasil). Medan magnet Bumi bekerja pada kompas, dan perputarannya di giroskop. Jadi jika Anda tidak memiliki kapal luar angkasa pribadi, Anda harus membuat sesuatu.

Solusi kedua yang langsung terlintas dalam pikiran adalah menempatkan sensor (atau lebih tepatnya porosnya) pada posisi di mana kita akan tahu persis apa yang harus ditunjukkan oleh sensor. Perbedaan antara apa yang ditunjukkan oleh sensor dan apa yang seharusnya ditampilkan - dan akan ada offset nol! Begitu? Sebagai contoh, kita tahu bahwa jika accelerometer ditempatkan pada level dengan horizon, maka secara teori, vektor percepatan gravitasi akan diarahkan tepat di sepanjang sumbu Z sensor. Besarnya vektor percepatan yang kita tahu.

Namun, ada masalah. Terdiri dari fakta bahwa kita tidak dapat secara tepat mengatur sumbu sensor ke level dengan horizon. Faktanya adalah bahwa permukaan yang akan kita andalkan tidak sejajar dengan papan sirkuit tercetak. Itu, pada gilirannya, tidak sejajar dengan situs di mana sensor berada. Sensor itu sendiri tidak berdiri tepat di tempatnya dan sumbu di dalam sensor tidak sejajar dengan badan sensor. Kesalahan dalam menyetel sumbu relatif terhadap cakrawala sebesar 1 derajat memberikan proyeksi yang sebanding ukurannya dengan nilai titik nol itu sendiri, yang ingin kami temukan. Dalam kasus magnetometer, kami juga tidak tahu di mana vektor medan magnet diarahkan. Secara teori, ke utara. Namun dalam praktiknya, medan magnet Bumi itu sendiri heterogen dalam intensitas dan arahnya. Plus, benda-benda logam di dekatnya membuat penyesuaian.


Pernyataan masalah dan metode solusi


Tugasnya adalah sebagai berikut: kita perlu menentukan vektor perpindahan nol menggunakan sensor, yang akan selalu merekam vektor perpindahan + vektor dampak eksternal konstan (percepatan gravitasi, rotasi bumi, medan magnet Bumi), besarnya dan arah yang tidak kita ketahui (dalam kasus akselerometer kita tahu nilainya, tetapi sekali lagi skala sensor mungkin tidak sama dengan 1).

Cara memecahkannya. Artikel ini mengusulkan untuk menentukan vektor perpindahan sebagai berikut. Kami mengambil dan memutar sensor dengan segala cara dan mendaftarkan pembacaan sensor. Setelah pengukuran N, nilai-nilai yang diambil dari sensor dan terletak pada grafik akan menjadi bola, jari-jari yang besarnya dampak eksternal, dan pusat adalah nol offset yang diinginkan tepat.

Bagaimana cara mendapatkan poin?


Untuk memudahkan prosedur pengukuran itu sendiri, Anda dapat menulis program sederhana. Seharusnya merekam sensor ketika perangkat stasioner. Kami hanya perlu mengubah perangkat ke posisi yang diinginkan. Untuk menentukan keadaan stasioner, accelerometer yang tidak dikalibrasi juga cocok - ambil saja selisih antara nilai saat ini dan yang sebelumnya. Dan jika ada lebih banyak suara, maka kita perbaiki gerakannya. Ambang saya diperoleh di wilayah 0,07G. Jika Anda memegang dengan tangan Anda, lebih dari nilai ini akan berubah. Saya menggunakan selotip untuk memperbaiki posisi. Jika masih tidak berhasil, periksa untuk melihat apakah ada lemari es, kipas angin atau sesuatu yang serupa di dekatnya.
Bagaimana bisa dalam kode
//       
static TSumSensorsData 	g_sens_data[2];
static int32_t   	g_sens_data_sum_cnt[2];
static uint8_t		g_sens_data_num;

//  - ,     
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
	SensorRawBuffer *raw = sensor_get_raw_buffer();
	g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
	g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
	g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
	g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
	g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
	g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
	g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
	g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
	g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
	g_sens_data_sum_cnt[g_sens_data_num]++;
}

//   main
void sensors_calibrate_program(FlashROM *flash_ptr)
{
	double calibrate_result_error[3];
	TVector16 calibrate_result[3];
	int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
	uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
	TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
	
        . . .

	//  
	g_sens_data_sum_cnt[0] = 0;
	g_sens_data_num = 0;
	int16_t prev_avg_x = 0;
	int16_t prev_avg_y = 0;
	int16_t prev_avg_z = 0;
	int8_t low_motion_cnt = 0;

	while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
	{
		if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
		{
			uint8_t new_data_num = (g_sens_data_num + 1) & 1;
			g_sens_data[new_data_num].acc_x = 0;
			g_sens_data[new_data_num].acc_y = 0;
			g_sens_data[new_data_num].acc_z = 0;
			g_sens_data[new_data_num].gyro_x = 0;
			g_sens_data[new_data_num].gyro_y = 0;
			g_sens_data[new_data_num].gyro_z = 0;
			g_sens_data[new_data_num].mag_x = 0;
			g_sens_data[new_data_num].mag_y = 0;
			g_sens_data[new_data_num].mag_z = 0;
			g_sens_data_sum_cnt[new_data_num] = 0;

			uint8_t old_data_num = g_sens_data_num;
			g_sens_data_num = new_data_num; //           
			// ( -    ,   )

			//     -  
			int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
			int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
			int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];

			//      
			int16_t dx = avg_x - prev_avg_x;
			int16_t dy = avg_y - prev_avg_y;
			int16_t dz = avg_z - prev_avg_z;
			prev_avg_x = avg_x;
			prev_avg_y = avg_y;
			prev_avg_z = avg_z;

			//     
			if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
			{
				//    
				raw[RAW_ACC][low_motion_cnt].x = avg_x;
				raw[RAW_ACC][low_motion_cnt].y = avg_y;
				raw[RAW_ACC][low_motion_cnt].z = avg_z;
				raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
				raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];

				low_motion_cnt++;

				//   
				beep();

				//     2   ,     -   
				//  -  
				//      
				delay_ms(2000);
			}
		}
	}
. . .
}


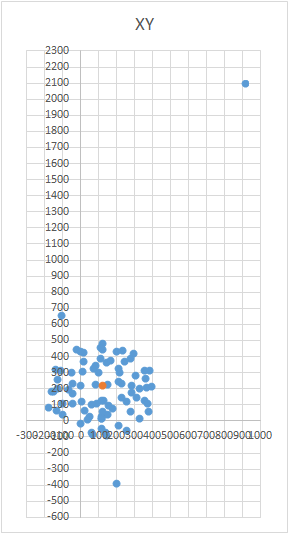
Untuk mendapatkan bola pada grafik, Anda perlu memutar perangkat dengan sensor sesuai skema tertentu. Untuk tujuan ini, globe sangat cocok, karena memiliki markup. Anda mungkin berpikir bahwa Anda perlu membuat patung di seluruh dunia. Tapi ini tidak benar.
Contoh hasil yang salah


Penting untuk memahat sensor tidak pada seluruh permukaan globe, tetapi pada satu meridian. Misalkan kita mengambil tujuh titik pada meridian (yang pertama dan terakhir di kutub utara dan selatan). Di setiap titik meridian, kami memasang perangkat Anda ke globe dan masih memutar perangkat di sekitar porosnya dengan langkah tertentu, misalnya 30-35 derajat. Ternyata jika Anda memutar 12 kali di sekitar porosnya, maka pada 7 titik total 84 pengukuran diperoleh.



Keindahan metode ini adalah bahwa segala sesuatu dapat dilakukan "di lutut". Akurasi posisi tidak memainkan peran khusus, Anda hanya perlu memutar sesuai skema sehingga vektor pengaruh eksternal pada grafik menarik bola. Yang benar terlihat seperti ini - lihat gambar (tengah ditandai dengan tanda).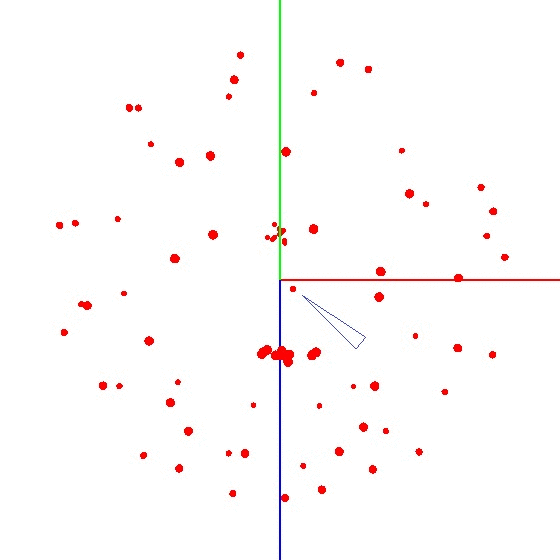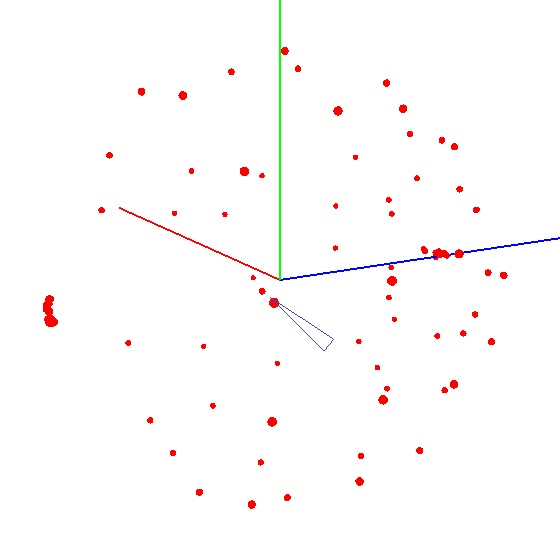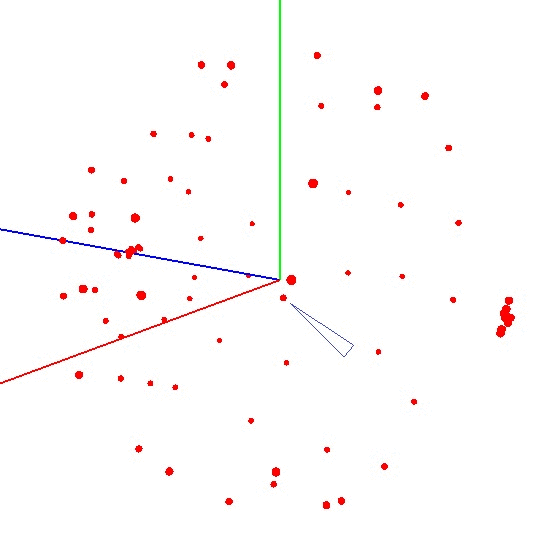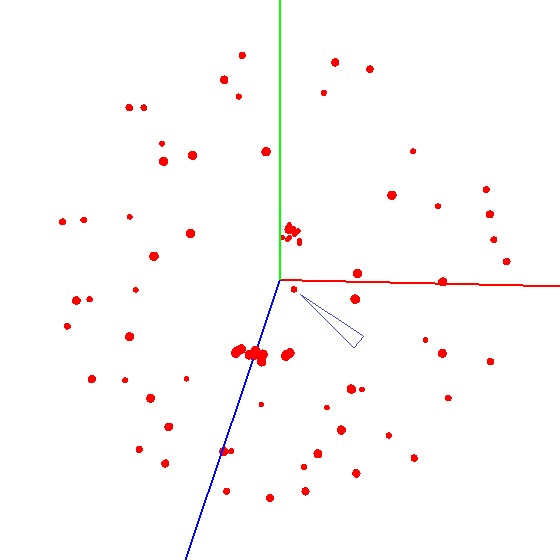



Bagaimana cara menghitung bagian tengah bola?


Ini adalah tugas yang menarik dan memiliki beberapa solusi. Tampaknya untuk mencari pusat, cukup untuk mengambil rata-rata aritmatika dari koordinat poin yang diperoleh. Namun, ini tidak demikian - poin-poinnya bisa terletak tidak rata pada bola (lihat Gambar.).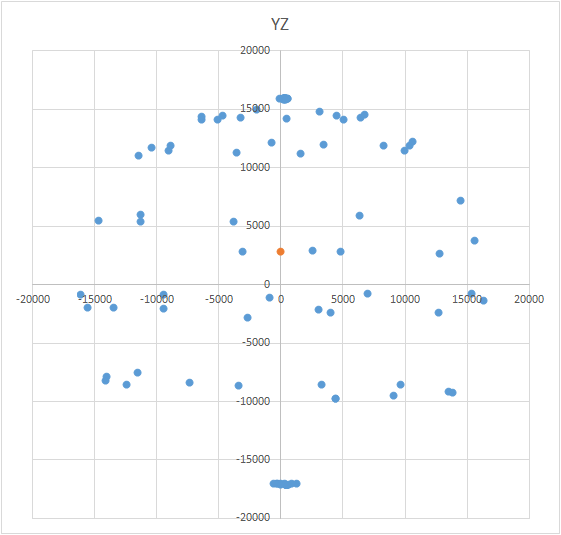



Persamaan bola terlihat seperti ini: (X - A) 2 + (Y - B) 2 + (Z - C) 2 = R 2 , di mana X, Y, Z adalah koordinat dari titik berbaring di bola. A, B, C adalah koordinat pusat pada sumbu x, y, dan z. R adalah jari-jari bola. Anda dapat membangun sistem persamaan dan mencoba menyelesaikan sistem ini lebih sederhana menggunakan beberapa metode. Atau Anda bisa langsung menemukan pusatnya (ini seperti metode perkiraan yang berurutan). Arti metode ini sederhana: nilai kesalahan (X - A) 2 + (Y - B) 2+ (Z - C) 2 - R 2 harus cenderung nol. Ini berarti bahwa jumlah jumlah ini untuk semua titik bola juga harus cenderung nol. Mengetahui hal ini, kita dapat memilih nilai A, B, dan C yang kesalahannya minimal untuk semua poin. Area pencarian dibatasi oleh ukuran bola (kubus kondisional). Artinya, kita harus secara berurutan meletakkan pusat bola di semua titik kubus dan menghitung kesalahannya. Di mana ada kesalahan minimal - ada pusatnya.



Sebagai R, kita perlu mengambil nilai teoritis dari vektor pengaruh luar - untuk akselerometer, ini adalah percepatan gravitasi, untuk kompas - ini adalah besarnya rata-rata medan magnet bumi, untuk giroskop - kecepatan rotasi Bumi. Tentu saja, dalam rumus harus ada nilai satu dimensi (unit konvensional sensor atau m / s 2, derajat / s, dll.). Lebih mudah mengonversi ke unit arbitrary dari sensor yang sesuai.
Bagaimana cara menghitung nilai tertentu dalam unit standar sensor?
= * / ( — )
: 16- ±2g ?:
9,8 /2 * 65536 / (2g + 2g) = 9,8 /2 * 65536 / (2 * 9,8 /2 + 2 * 9,8 /2) = 16384 . . .

Ngomong-ngomong, jika Anda tahu jari-jari bola dengan tepat, maka Anda dapat menghitung pusat hanya dengan "baji". Yaitu, pada titik-titik yang terletak hanya pada selembar permukaan bola. Tapi ini bukan kasus kami.

Bagaimana cara mempercepat pencarian pusat bola?


Penting untuk mencari pusat bukan di seluruh kubus (dimensi bola), tetapi sepanjang garis yang permulaannya sewenang-wenang, setiap titik berikutnya lebih dekat ke pusat nyata dan ujungnya di tengah. Misalkan kita mulai dari titik (0; 0; 0) ... Kita selalu bergerak dengan langkah yang konstan. Oleh karena itu, jika kita membayangkan satu set kubus 3x3x3, di mana setiap wajah sama dengan ukuran langkah dan juga membayangkan bahwa posisi saat ini adalah kubus tengah, maka kita memiliki 9 + 8 + 9 opsi tempat untuk meletakkan titik berikutnya. Kita hanya harus berada di setiap titik, untuk menghitung di mana dari 26 titik tetangga kesalahannya akan lebih kecil. Jika ternyata kesalahannya kurang pada titik saat ini, dan bukan di salah satu yang tetangga, maka itu berarti bahwa itu adalah di tengah dan pencarian sudah selesai.


Bagaimana bisa dalam kode
Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
    x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
    y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
    z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
    get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function

. . .
A = 0
B = 0
C = 0

Do While True
   min_sigma = 0
    For ai = -1 To 1
        For bi = -1 To 1
            For ci = -1 To 1
                sigma = get_err(A + ai, B + bi, C + ci, 16384)
                If sigma < min_sigma Or min_sigma = 0 Then
                    ai_min = ai
                    bi_min = bi
                    ci_min = ci
                    min_sigma = sigma
                End If
            Next
        Next
    Next
    
    If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
        Exit Do
    End If
    
    A = A + ai_min
    B = B + bi_min
    C = C + ci_min
Loop
. . .



Bagaimana lagi untuk mempercepat pencarian pusat bola?


Perlu mencari dengan nada variabel. Pertama kita mencari pusat di langkah besar. Kami menemukan pusat, kami mengurangi langkah dan dari sana kami mulai mencari lebih jauh. Dan seterusnya, sampai Anda mendapatkan hasil dari akurasi yang diperlukan.
Bagaimana bisa dalam kode
Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
    x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
    y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
    z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
    get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
   min_sigma = 0
    For ai = -1 To 1
        For bi = -1 To 1
            For ci = -1 To 1
                sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
                If sigma < min_sigma Or min_sigma = 0 Then
                    ai_min = ai
                    bi_min = bi
                    ci_min = ci
                    min_sigma = sigma
                End If
            Next
        Next
    Next
    If ai_min = 0 And bi_min = 0 And ci_min = 0 Then        
        step = step / 10
        If step < 0.01 Then
            Exit Do
        End If
    Else
    A = A + ai_min * step
    B = B + bi_min * step
    C = C + ci_min * step
    End If
Loop
. . .



Tentang kesalahan pengukuran


Selama pengukuran, mungkin ada situasi di mana, untuk beberapa alasan, hasil pengukuran mungkin jauh lebih jauh dari permukaan bola. Atau bisa banyak poin. Atau, secara umum, hasil pengukuran mungkin bukan bola, tetapi "telur" atau "airship". Dalam hal ini, tentu saja, Anda perlu mengulang semua pengukuran, mengidentifikasi kemungkinan penyebab kesalahan. Misalnya, untuk magnetometer dapat berupa baut atau paku di meja dan Anda melakukan pengukuran langsung di atasnya. Dan semakin rendah Anda menurunkan sensor di sepanjang meridian, semakin kuat logam akan mempengaruhi hasilnya. Oleh karena itu, perlu untuk menentukan ambang batas nilai kesalahan yang diizinkan. Agar tidak mengulangi pengukuran karena beberapa titik yang keliru jelas, Anda dapat menerapkan filter. Prinsip filter ini sangat sederhana - setelah menghitung pusat untuk pertama kalinya, urutkan poin berdasarkan tingkat kesalahan di masing-masingnya.Beberapa poin dengan kesalahan terbesar dapat dengan mudah dibuang (misalnya, 10%). Maka Anda perlu mengulangi pencarian untuk pusat.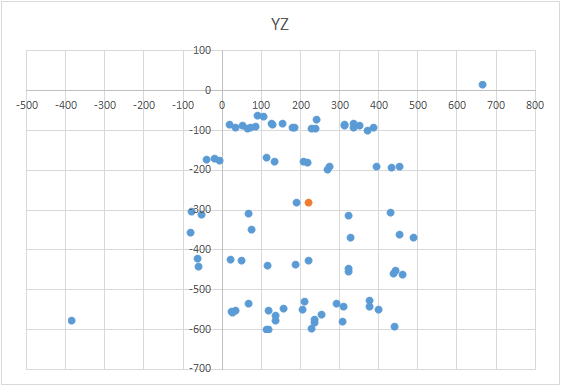


Total


Metode ini memiliki akurasi yang cukup baik. Metode ini memungkinkan Anda melakukan dengan cara improvisasi sederhana (bola, bank, dll.). Ini bekerja cukup cepat. Kode sederhana Banyak sensor memiliki register khusus di mana Anda dapat menulis nilai yang ditemukan, dan sensor akan menguranginya dengan cepat. Register semacam itu biasanya memiliki awalan "TRIM", seperti pada MPU9260, atau "OFFSET", seperti pada LSM303. Tetapi LIS302DL yang terkenal tidak memiliki register seperti itu.

Jangan lupa beri tanda plus jika Anda menyukainya. Tulis dalam komentar metode Anda untuk mengkalibrasi sensor.

Source: https://habr.com/ru/post/id384075/

More articles:


All Articles