Geekly articles weekly

Fabric ruang-waktu kuantum: jaringan permadani

Bagaimana pasangan kuantum menjahit ruangwaktu




Bagian pertama,

Brian Swingle belajar fisika di sekolah pascasarjana Massachusetts Institute of Technology, ketika dia memutuskan untuk mengambil beberapa kelas dalam teori string untuk meningkatkan pendidikannya - seperti yang dia ingat, pada prinsip "kenapa tidak" - walaupun dia awalnya tidak memperhatikan konsep siapa yang dia temui pada kursus ini. Tetapi karena tenggelam lebih dalam, dia mulai memperhatikan hubungan tak terduga dengan karyanya sendiri, di mana dia menggunakan apa yang disebut jaringan tensor untuk memprediksi sifat bahan eksotis dan pendekatan fisika lubang hitam dan gravitasi kuantum, diambil dari teori string. "Saya menyadari sesuatu yang luar biasa sedang terjadi," katanya.

Tensor secara berkala tiba-tiba muncul di berbagai bidang fisika - ini adalah objek matematika yang dapat mewakili banyak angka sekaligus. Misalnya, vektor kecepatan adalah tensor yang paling sederhana: ini mencakup kecepatan dan arah. Tensor yang lebih kompleks yang terhubung dalam jaringan dapat digunakan untuk menyederhanakan perhitungan untuk sistem kompleks yang terdiri dari banyak bagian yang berinteraksi - termasuk interaksi rumit dari sejumlah besar partikel subatomik yang membentuk materi.

Swing adalah salah satu dari jumlah fisikawan yang semakin meningkat yang melihat nilai penerapan jaringan tensor ke kosmologi. Di antara manfaat lainnya, ini dapat membantu menyelesaikan perdebatan yang sedang berlangsung tentang esensi ruang-waktu. John PreskillProfesor Richard Feynman dari Fisika Teoritis di KalTech percaya bahwa banyak fisikawan mencurigai adanya hubungan yang mendalam antara keterikatan kuantum - aksi jarak jauh yang menakutkan yang membuat Einstein begitu marah - dan geometri ruang-waktu pada skala terkecil. Ini telah terjadi sejak John Wheeler, enam puluh tahun yang lalu, pertama kali menggambarkan ruang-waktu sebagai busa yang menggelegak. "Jika Anda mempelajari geometri pada skala yang sebanding dengan skala Planck" - pada jarak sesingkat mungkin - "itu terlihat semakin mirip ruang-waktu," kata Preskill. "Ini bukan geometri sama sekali, tetapi sesuatu yang lain, sesuatu yang muncul dari hal-hal yang lebih mendasar."

Fisikawan terus berjuang dengan masalah membingungkan tentang apa masalah yang lebih mendasar ini, tetapi mereka curiga bahwa itu terkait dengan informasi kuantum. “Ketika kita berbicara tentang pengkodean informasi, kami maksudkan bahwa Anda dapat membagi sistem menjadi beberapa bagian dan akan ada korelasi di antara mereka sehingga saya dapat mempelajari sesuatu tentang salah satu bagian, mengawasi yang lain,” kata Preskill. Inilah esensi kebingungan.

Mereka sering berbicara tentang "bahan" ruang-waktu, dan metafora ini mengarah pada konsep menjahit masing-masing benang menjadi satu kesatuan yang halus. Utas ini pada dasarnya adalah kuantum. "Keterikatan adalah jalinan ruangwaktu," kata Swingle, saat ini sedang mengerjakan penelitian di Stanford. - Ini adalah utas yang mengikat seluruh sistem bersama-sama, memastikan perbedaan antara properti umum dan properti entitas individu. Tetapi untuk benar-benar melihat perilaku kolaboratif yang menarik, Anda perlu memahami bagaimana keterjeratan didistribusikan. "

Jaringan Tensor menyediakan alat matematika yang dapat melakukan hal itu. Dari sudut pandang ini, ruang-waktu muncul dari set node dari jaringan kompleks yang terhubung satu sama laindi mana potongan-potongan kecil informasi kuantum cocok bersama seperti Lego. Keterikatan adalah lem yang menghubungkan jaringan. Untuk memahami ruang-waktu, pertama-tama perlu mempertimbangkan keterjeratan dari posisi geometris, karena ini adalah bagaimana informasi dikodekan dalam sejumlah besar node sistem yang berinteraksi.

Banyak badan, satu jaringan


Memodelkan sistem kuantum yang kompleks bukanlah lelucon; bahkan sistem klasik dengan lebih dari dua bagian yang saling berinteraksi sudah cukup rumit untuk pemodelan. Ketika Isaac Newton menerbitkan Principia [Prinsip-prinsip Matematika Filsafat Alam] pada tahun 1687, salah satu tema buku ini adalah "masalah tiga tubuh". Tugas menghitung gerak dua objek, misalnya, Matahari dan Bumi, dengan mempertimbangkan ketertarikan bersama mereka, relatif sederhana. Tetapi jika Anda menambahkan tubuh ketiga ke dalamnya - misalnya, Bulan - itu berubah dari tugas sederhana dengan solusi tepat ke kacau, di mana prediksi jangka panjang membutuhkan sistem komputasi yang kuat untuk mensimulasikan perkiraan evolusi sistem. Dan semakin banyak objek dalam sistem, semakin rumit perhitungannya, dan kompleksitasnya tumbuh hampir secara linear - setidaknya dalam fisika klasik.

Sekarang bayangkan sebuah sistem kuantum dengan miliaran atom, yang masing-masing berinteraksi dengan yang lain sesuai dengan persamaan kuantum yang kompleks. Pada skala ini, kompleksitas tampaknya tumbuh secara eksponensial dengan jumlah partikel dalam sistem, sehingga pendekatan brute force untuk komputasi tidak akan berfungsi.

Bayangkan sebuah nugget emas. Terdiri dari miliaran atom, dan mereka semua berinteraksi satu sama lain. Dari interaksi ini, berbagai sifat klasik logam mengikuti - warna, kekuatan, atau konduktivitas. "Atom adalah hal-hal kecil yang mematuhi mekanika kuantum, dan ketika Anda menyatukannya, hal-hal baru dan menakjubkan terjadi," kata Swingle. Tetapi pada skala ini, aturan mekanika kuantum mulai bekerja. Fisikawan perlu secara akurat menghitung fungsi gelombang nugget ini, yang menggambarkan keadaan sistem. Dan fungsi ini adalah hydra berkepala banyak dari kompleksitas eksponensial.

Sekalipun hanya ada seratus atom dalam nugget dan masing-masing atom memiliki putaran kuantum yang mengambil satu dari dua keadaan, naik atau turun, jumlah total keadaan yang mungkin akan menjadi 2.100juta triliun triliun. Dan dengan penambahan setiap atom, tugas memburuk secara eksponensial. (Dan itu menjadi lebih buruk ketika Anda mencoba menggambarkan sesuatu selain spin, seperti yang harus dilakukan oleh setiap model realistis). "Jika Anda mengambil seluruh Universe yang terlihat dan mengisinya dengan drive terbaik yang tersedia, hard drive terbaik, Anda dapat menyimpan hanya 300 putaran pada mereka," kata Swingle. - Ada informasi, tetapi tidak semuanya sesuai dengan fisika. Tidak ada yang pernah mengukur angka-angka ini. "

Jaringan tensor memungkinkan fisikawan untuk mengompres semua informasi yang terkandung dalam fungsi gelombang dan hanya berkonsentrasi pada sifat-sifat yang dapat diukur secara eksperimental: seberapa banyak materi memantulkan cahaya, atau seberapa baik menyerap suara, atau bagaimana ia menghantarkan listrik. Tensor adalah kotak hitam yang mengambil satu set angka dan memberikan yang lain. Oleh karena itu, Anda dapat menghubungkan fungsi gelombang sederhana - misalnya, banyak elektron yang tidak berinteraksi satu sama lain dalam keadaan dengan energi terendah - dan memprosesnya dengan tensor berulang-ulang hingga proses menghasilkan fungsi gelombang untuk sistem yang besar dan kompleks, seperti miliaran yang berinteraksi dalam nugget atom emas. Hasilnya adalah diagram sederhana yang mewakili nugget kompleks ini - inovasi,sebanding dengan diagram yang dikembangkan oleh Feynman pada pertengahan abad ke-20 yang menyederhanakan representasi interaksi partikel. Dan jaringan tensor memiliki geometri sendiri, serta ruang-waktu.

Kunci penyederhanaan terletak pada prinsip "lokalitas". Setiap elektron individu berinteraksi hanya dengan elektron terdekat. Keterikatan masing-masing elektron dengan tetangganya memberikan satu set "node" dari jaringan. Node-node ini adalah tensor dan keterikatan mengikat keduanya. Semua node yang saling terhubung ini membentuk jaringan. Perhitungan yang rumit menjadi lebih mudah untuk divisualisasikan. Kadang-kadang turun ke tugas menghitung yang lebih sederhana.

Ada banyak jenis jaringan tensor, tetapi di antara yang paling berguna ada satu yang dikenal dengan singkatan MERA (anzats renormalization of multiscale entanglement). Prinsip operasinya adalah sebagai berikut: bayangkan garis elektron satu dimensi. Ganti delapan elektron yang berbeda - dinotasikan oleh A, B, C, D, E, F, G dan H - dengan unit dasar informasi kuantum (qubit) dan hubungkan masing-masing dengan tetangga untuk membentuk ikatan. A menjadi bingung dengan B, C dengan D, dan sebagainya. Ini menghasilkan jaringan level yang lebih tinggi. Kemudian bingung AB dengan CD dan EF dengan GH untuk naik lapisan jaringan yang lain. Dan akhirnya, ABCD menjadi bingung dengan EFGH untuk membentuk level tertinggi. "Dalam arti tertentu, kita dapat mengatakan bahwa keterjeratan digunakan untuk membangun fungsi gelombang banyak tubuh," tulis Roman Orus dalam karyanya tahun lalu [Román Orús ], seorang ahli fisika dari Universitas. Johannes Gutenberg (Jerman).

Mengapa beberapa fisikawan begitu optimis tentang potensi jaringan tensor - terutama MERA - yang dapat mengarahkan mereka ke gravitasi kuantum? Karena jaringan menunjukkan bagaimana struktur geometris sederhana dapat muncul dari interaksi kompleks antara banyak objek. Dan Swingle dengan orang-orang yang berpikiran sama berharap bahwa geometri baru ini dapat digunakan, menunjukkan bagaimana hal itu menjelaskan mekanisme di mana masing-masing informasi kuantum diubah menjadi ruang-waktu yang halus dan kontinu.

Batas ruang-waktu


Ketika mengembangkan jaringan tensor, para ahli dalam fisika benda terkondensasi secara tidak sengaja menemukan dimensi tambahan: teknik ini mengarah pada penampilan sistem dua dimensi dalam satu dimensi. Dan para ahli dalam teori gravitasi menghilangkan satu dimensi - bergerak dari tiga ke dua - mengembangkan apa yang disebut prinsip holografik. Dua konsep ini dapat bersatu dan menciptakan pandangan ruang-waktu yang lebih kompleks.

Pada 1970-an, fisikawan Jacob Bekenstein menunjukkan bahwa informasi tentang bagian dalam lubang hitam dikodekan pada permukaan dua dimensi yang datar (pada batas), dan bukan dalam volume tiga dimensi. Dua puluh tahun kemudian, Leonard Susskind dan Gerard 't Hooft [Leonard Susskind dan Gerard' t Hooft] memperluas konsep ini ke seluruh Semesta, menyamakannya dengan hologram: Semesta tiga dimensi kita dalam semua kemegahannya muncul dari "kode sumber" dua dimensi. Pada tahun 1997, Juan Maldacena menemukan contoh konkret dari pengoperasian hologram, menunjukkan bahwa model mainan untuk menggambarkan ruang datar tanpa gravitasi setara dengan menggambarkan ruang berbentuk pelana dengan gravitasi. Hubungan fisika ini disebut "dualitas."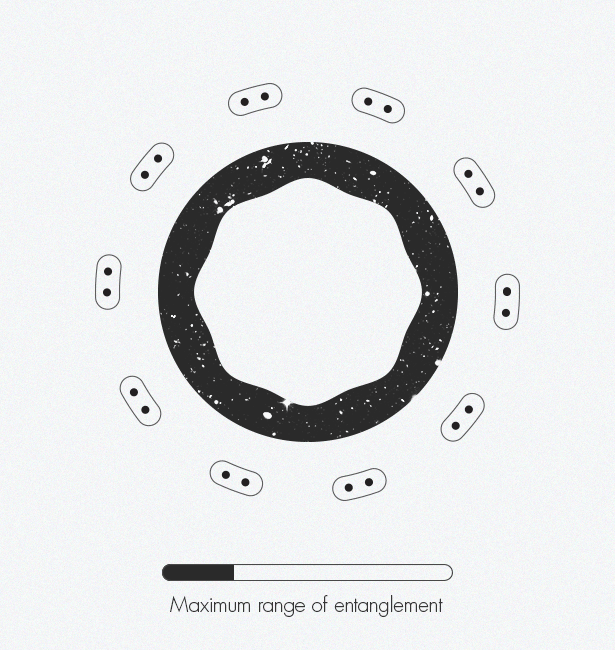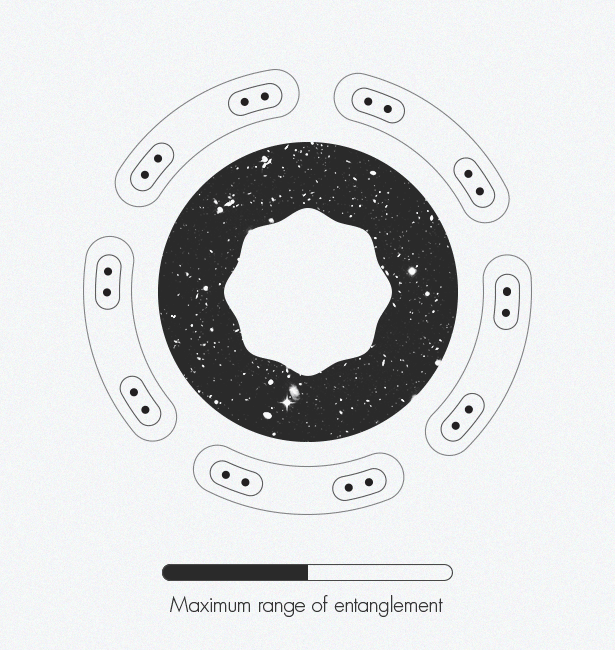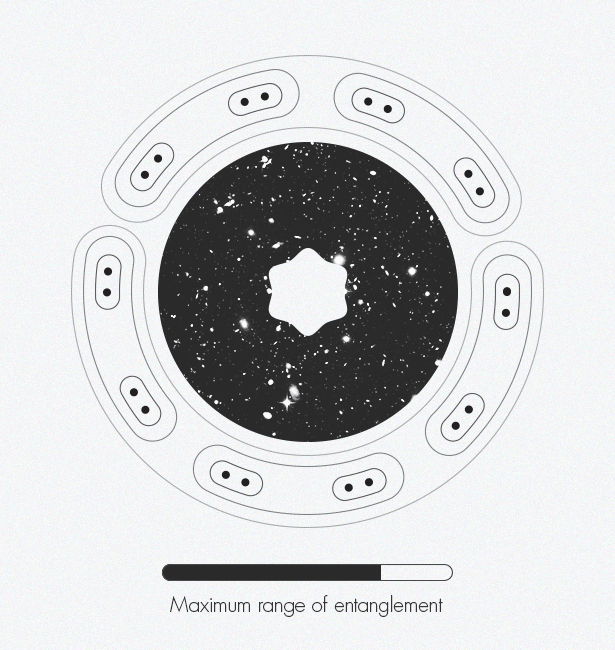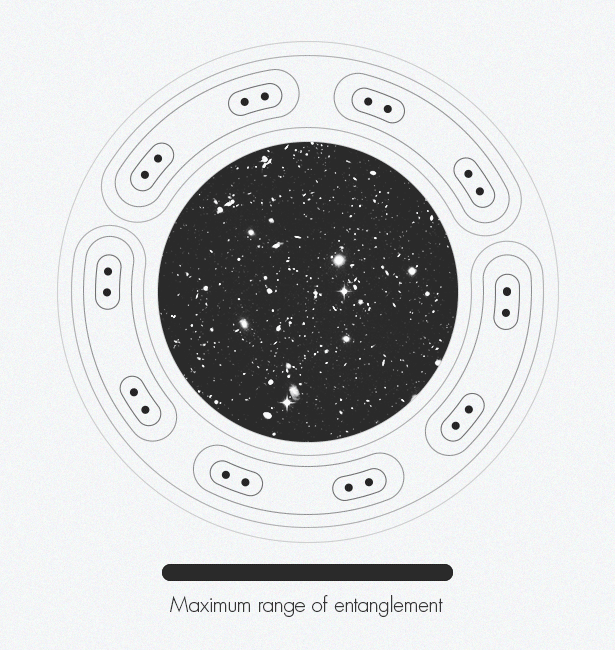


Mark Van Raamsdonk [ Mark Van Raamsdonk] menggambarkan bagaimana keterikatan secara bertahap menciptakan ruangwaktu. Di sepanjang tepi gambar, partikel titik individu mulai menjadi terjerat satu sama lain. Pasangan terjerat ini terjerat dengan pasangan lainnya. Ketika semakin banyak pasangan terjerat, struktur ruang-waktu muncul.

Mark van Raamsdonck, spesialis teori string di University of British Columbia (Vancouver), membandingkan prinsip holografik ini dengan chip komputer dua dimensi yang berisi kode untuk menciptakan dunia virtual tiga dimensi dalam permainan komputer. Kami tinggal di dalam ruang tiga dimensi permainan. Dalam arti tertentu, ruang kita ilusi dan hanya gambar sesaat yang menggantung di udara. Tetapi van Raamsdonck menekankan bahwa "masih ada semacam entitas fisik di komputer yang menyimpan semua informasi."

Gagasan ini telah diterima secara luas di kalangan fisikawan teoretis, tetapi mereka masih berjuang dengan bagaimana tepatnya dimensi yang lebih kecil menyimpan informasi tentang geometri ruang-waktu. Tangkapannya adalah bahwa chip komputer metaforis kami harus menjadi semacam komputer kuantum, di mana nol dan yang biasa digantikan oleh qubit, yang mampu secara simultan mewakili semua keadaan yang mungkin dari nol menjadi satu. Qubit-qubit ini harus dilibatkan - sehingga keadaan satu qubit ditentukan oleh keadaan tetangganya - sebelum dunia tiga dimensi yang realistis dapat dikodekan.

Demikian pula, keterjeratan tampaknya menjadi fitur mendasar ruangwaktu. Dua ilmuwan sampai pada kesimpulan ini pada tahun 2006: Shinsei Ryu (Universitas Illinois) dan Tadashi Takayanagi (Universitas Kyoto), yang berbagi penghargaan New Horizons of Physics pada tahun 2015. "Idenya adalah bahwa cara geometri ruang-waktu dikodekan sangat terkait dengan bagaimana bagian-bagian berbeda dari chip ini terjerat satu sama lain," jelas Van Raamsdonk.

Terinspirasi oleh karya mereka, serta karya Maldasena yang mengikuti, pada 2010, Van Raamsdonk mengusulkan eksperimen pemikiran yang menunjukkan peran penting keterjeratan dalam pembentukan ruang-waktu. Dia menyelidiki apa yang akan terjadi jika Anda membagi chip komputer menjadi dua, dan kemudian menghapus keterikatan antara qubit di dua bagian. Dia menemukan bahwa ruang-waktu mulai runtuh dengan cara yang sama bahwa peregangan sepotong permen karet pada ujungnya mengarah ke celah di tengah. Membagi chip ini menjadi bagian-bagian yang lebih kecil dan lebih kecil memecah ruang waktu sampai hanya bagian-bagian yang terpisah dan tidak terhubung yang tersisa. "Jika Anda menghilangkan kebingungan, ruang-waktu akan berantakan," kata Van Raamsdonk. Demikian pula, "jika Anda ingin membangun ruang-waktu,Anda harus membingungkan qubit dengan cara tertentu. "

Gabungkan pemikiran-pemikiran ini dengan karya Swingle, yang menghubungkan struktur ruang-waktu yang rumit dan prinsip holografik dengan jaringan tensor dan potongan puzzle lainnya yang sesuai dengan tempatnya. Ruang-waktu melengkung secara alami muncul dari keterikatan dalam jaringan tensor melalui holografi. "Ruang-waktu adalah representasi geometris dari informasi kuantum ini," kata van Raamsdonk.

Dan seperti apa bentuk geometri ini? Dalam kasus ruang-waktu berbentuk sadel Maldasena, sepertinya salah satu gambar "batas - lingkaran" oleh Escher dari tahun 1950-1960-an. Escher telah lama tertarik pada keteraturan dan simetri, termasuk konsep-konsep matematika ini dalam karyanya sejak 1936, ketika ia mengunjungi arsitektur Alhambra dan ansambel taman di Spanyol dan menemukan inspirasi dalam pola ubin berulang di sana, khas arsitektur Moor, yang dikenal sebagai mosaik.

Ukirannya pada pohon "batas - lingkaran" menggambarkan geometri hiperbolik: distorsi ruang dengan kelengkungan negatif pada permukaan dua dimensi piringan menyerupai perataan bola bumi ke peta dua dimensi Bumi, mendistorsi bentuk benua. Misalnya, " batas - lingkaran IV"(neraka dan surga) terlihat seperti banyak figur malaikat dan setan yang berulang. Di ruang hiperbolik ukuran semua angka akan sama, tetapi dalam representasi dua dimensi dari Escher, angka-angka di tepi terlihat lebih kecil daripada di tengah. Diagram jaringan tensor sangat mirip dengan seri" batas " - circle ”, representasi visual dari koneksi mendalam yang ditemukan Swing saat menghadiri kelas-kelas teori string yang sama.

Saat ini, analisis tensor terbatas pada pemodelan ruang-waktu (seperti dalam Maldasena), yang tidak menggambarkan Alam Semesta tempat kita hidup - ia tidak memiliki bentuk pelana, dan perluasannya semakin cepat. Fisikawan dapat menerjemahkan antar model hanya dalam kasus-kasus khusus yang terpisah. Idealnya, mereka membutuhkan "kamus" universal. Dan mereka ingin menurunkan kamus ini secara langsung, tanpa menggunakan perkiraan. “Kami berada dalam posisi lucu dengan dualitas ini karena semua orang setuju bahwa mereka sangat penting, tetapi tidak ada yang tahu bagaimana mengeluarkannya,” kata Preskill. “Mungkin pendekatan jaringan tensor akan membuat kemajuan lebih lanjut menjadi mungkin. Saya pikir tanda kemajuan adalah jika kita dapat mengatakan, bahkan jika dalam kasus model mainan: 'Aha! Ini dia, kesimpulan dari kamus! ' Ini akan menjadi petunjuk serius bahwa kami menemukan sesuatu yang penting. "

Selama setahun terakhir, Swingle dan van Raamsdonk telah bekerja bersama untuk mempromosikan karya mereka di area yang memanjang dari representasi statis ruang-waktu menjadi dinamis. Mereka tertarik pada bagaimana ruang-waktu berubah dengan waktu dan bagaimana ia menekuk dalam menanggapi perubahan-perubahan ini. Sejauh ini mereka telah berhasil menurunkan persamaan Einstein, khususnya, prinsip kesetaraan. Ini membuktikan bahwa dinamika ruang-waktu, seperti geometrinya, didasarkan pada qubit yang rumit. Permulaannya menjanjikan.

"Pertanyaan 'Apa itu ruang-waktu?' tampaknya benar-benar filosofis, kata van Raamsdonk. "Bahkan, untuk menemukan jawaban yang konkret dan memungkinkan Anda untuk menghitung ruang-waktu - itu akan luar biasa."

Source: https://habr.com/ru/post/id396389/

More articles:


All Articles