👩🏼‍🚀 👩🏿‍⚕️ 🧝🏽 Kami mendapatkan bentuk: dari geometri hiperbolik ke kompleks kubik dan sebaliknya 🥢 ⏭️ ⏪

Buktinya menandai akhir suatu era dalam studi bentuk tiga dimensi.

Tiga puluh tahun yang lalu, ahli matematika William Thurston berbicara tentang visinya: mensistematisasikan semua kemungkinan bentuk tiga dimensi hingga.

Thurston, pemegang Fields Prize, yang menghabiskan sebagian besar karirnya di Universitas Princeton dan Cornell, memiliki kemampuan supranatural untuk mewakili yang tak terbayangkan: tidak hanya bentuk yang hidup di ruang tiga dimensi yang biasa, tetapi juga banyak sekali bentuk hewan peliharaan yang memiliki sifat kompleks sehingga mereka hanya bisa masuk ruang dengan banyak dimensi. Di mana matematikawan lain melihat permulaan bentuk, Thurston melihat struktur: simetri, permukaan, hubungan antara tokoh yang berbeda.

William Thurston di Berkeley pada tahun 1991.

"Setelah bertahun-tahun belajar, banyak orang memiliki kesan bahwa matematika adalah subjek yang ketat dan formal yang berkaitan dengan aturan yang kompleks dan tidak jelas," tulisnya pada tahun 2009. "Matematika yang bagus adalah kebalikan dari itu." Matematika adalah seni pemahaman manusia ... Matematika bernyanyi ketika kita merasakannya dengan seluruh otak kita. ”

Visi Thurston didasarkan pada perkawinan antara dua pendekatan yang tampaknya berbeda untuk mempelajari angka tiga dimensi: geometri, kerajaan sudut, panjang, wilayah dan volume yang akrab, dan topologi yang mempelajari sifat-sifat bentuk yang tidak tergantung pada pengukuran geometris yang akurat - properti yang tidak berubah jika bentuknya diregangkan atau dipelintir, seperti " pegangan ".

Untuk ahli topologi, permukaan wajan setara dengan permukaan meja, pensil, atau bola; permukaan cangkir setara dengan donat atau torus. Dari sudut pandang seorang ahli topologi, variasi bentuk dua dimensi - permukaan - turun ke daftar kategori sederhana: bola, toroidal, dan toroidal dengan sejumlah besar lubang. (Sebagian besar dari kita menyajikan bola dan tori sebagai tiga dimensi, tetapi karena matematikawan menganggapnya sebagai permukaan berongga, mereka menganggap permukaan ini sebagai objek dua dimensi, diukur dengan luas permukaan, bukan volume).

Gagasan kunci Thurston adalah untuk memahami manifold 3mungkin melalui penyatuan geometri dan topologi. Dengan cara yang sama bahwa kategori topologi 2-manifold, yang berisi permukaan wajan dan pensil, juga mengandung bola yang ideal, Thurston menyarankan bahwa banyak kategori 3-manifold berisi satu contoh, 3-manifold yang geometrinya begitu homogen dan sempurna, begitu indah bahwa, seperti yang dikatakan Walter Neumann dari Universitas Columbia, dia “berdering seperti bel.” Selain itu, Thurston menyarankan bahwa bentuk-bentuk yang tidak memiliki instance seperti itu dapat dipotong-potong di mana sudah akan menjadi.

Dalam makalah 1982, Thurston mengemukakan "hipotesis geometriasinya" di antara 23 pertanyaan tentang manifold 3 yang menawarkan ahli matematika arah pengetahuan bentuk tiga dimensi. (Ada 24 pertanyaan dalam daftar, tetapi salah satunya, masih belum terselesaikan, lebih seperti lorong yang menarik daripada jalan utama).

“Thurston memiliki bakat besar untuk mengajukan pertanyaan yang tepat,” kata Vladimir Markovich, ahli matematika dari Caltech. "Semua orang dapat mengajukan pertanyaan, tetapi jarang terjadi pertanyaan yang mengarah pada wawasan dan keindahan, sama seperti pertanyaan Thurston berhasil."

Pertanyaan menginspirasi generasi baru ahli matematika, puluhan di antaranya memutuskan untuk melakukan pekerjaan mereka di bawah arahan Thurston. “Anak-anak” matematisnya mengekspresikan gayanya, seperti yang ditulis Richard Brown.dari Universitas. John Hopkins. "Mereka memandang matematika, seperti anak-anak di pasar malam: dengan suka cita dan kejutan, terpesona oleh setiap penemuan baru, dan mereka senang menjadi bagian dari semuanya."

Puluhan tahun setelah kemunculan karya Thurston, matematikawan mengikuti "peta" penelitiannya, dan motivasi mereka tidak banyak dipengaruhi oleh aplikasi yang mungkin dari penemuan mereka, melainkan oleh tempat yang baik dimana manifold 3 ditempati dalam studi bentuk. Bentuk dua dimensi cukup lumrah, mereka mudah digambarkan dan dibagi menjadi beberapa kategori. Empat, lima, dan lebih banyak bentuk multidimensi praktis tidak mungkin untuk dilatih sama sekali: variasi kemungkinan sangat besar sehingga matematikawan membatasi diri mereka hanya untuk mengetahui subkelas khusus mereka. Dan dalam kasus bentuk tiga dimensi struktur, di satu sisi, mereka misterius dan sulit, tetapi di sisi lain, mereka secara mendasar dapat dikenali.

Karya Thurston telah melewati 30 tahun, dan semua kecuali empat masalah telah diselesaikan, termasuk hipotesis geometriisasi, dibuktikan oleh ahli matematika Rusia Grigory Perelman pada tahun 2002, yang merupakan pencapaian penting dalam matematika modern. Tetapi empat tugas yang tersisa dengan keras kepala menolak.

"Fakta bahwa kita belum mampu menyelesaikannya begitu lama berarti ada sesuatu yang sangat dalam tersembunyi di sana," kata Yair Minsky dari Universitas Yale.

Akhirnya, pada bulan Maret 2012, Ian Aigol dari University of California di Berkeley membangkitkan komunitas matematika dengan mengumumkan bukti hipotesis Wise yang mencakup empat pertanyaan terakhir Thurston dalam satu gerakan.

Matematikawan menyebut hasil ini sebagai akhir suatu era.

"Visi 3-manifold yang dijelaskan oleh Thurston dalam karyanya pada waktu itu mungkin tampak fantastis, tetapi sekarang sepenuhnya disadari," kata Danny Calegari dari Caltech. "Gagasannya terbukti secara mengejutkan - dan setiap detail benar."

“Tampak bagi saya bahwa ada pengetahuan khusus dan metode berpikir khusus yang hanya saya miliki,” tulis Thurston, setelah menerima hadiah matematika Steele hanya beberapa bulan sebelum kematiannya pada Agustus 2012 pada usia 65 tahun . "Dan saya sangat senang bahwa saya telah mencapai tingkat ketika ini tidak begitu - banyak orang berbagi cara berpikir saya, dan banyak membuktikan teorema yang saya gagal lakukan."

Prestasi Aigol menunjukkan adanya skema sederhana untuk membangun semua manifold hiperbolik 3 kompak - satu-satunya tipe bentuk tiga dimensi yang belum sepenuhnya dijelaskan.

"Kami sekarang mengerti persis seperti apa bentuk 3 manifold itu," kata Henry Wilton dari London University College. "Ini adalah puncak dari kisah sukses besar matematika."

Studi permukaan

Program Thurston coba lakukan dengan 3-manifold apa yang berhasil dilakukan oleh matematikawan seratus tahun yang lalu dengan manifold dua dimensi. Untuk meregangkan diri sebelum memahami manifold tiga dimensi, mari kita lihat bagian dalam klasifikasi permukaan "berorientasi kompak" (permukaan terbatas tanpa tusukan dan pemotongan dengan orientasi konstan).

Untuk mendekati masalah klasifikasi, matematikawan telah menunjukkan bahwa untuk permukaan apa pun dimungkinkan untuk melakukan penyederhanaan berurutannya dengan memotong sepanjang kurva sampai terbuka menjadi poligon datar.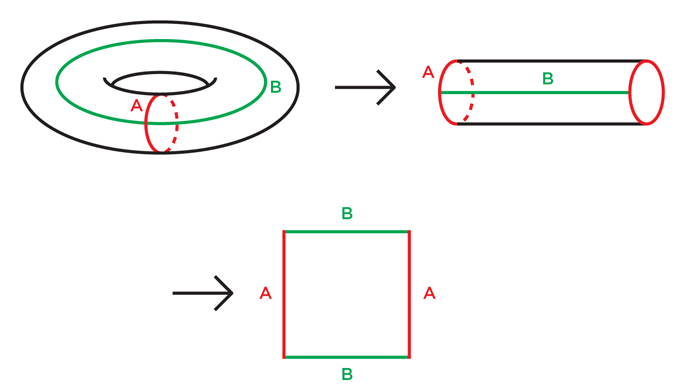

Fig. 1

Sangat mudah untuk menunjukkan ini untuk torus: pertama kita memotongnya sepanjang loop A, seperti pada Gambar. 1, kita mendapatkan silinder. Lalu kami memotong sepanjang lingkaran B, meluruskan silinder menjadi persegi. Gambar 2 sedikit lebih sulit untuk diketahui, tetapi bahkan di sana, memotong sepanjang empat kurva mengubah torus ganda (torus dengan dua lubang) menjadi segi delapan. Dengan cara yang sama, untuk torus apa pun dengan lubang n, kita dapat membuat 2n takik di loop dan memperluasnya menjadi 4n-gon.

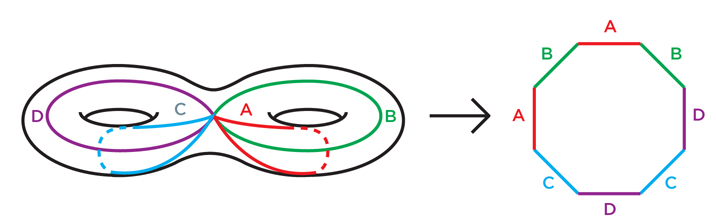Gbr.2

Anda dapat mencoba menyederhanakan permukaan tak terbatas sembarang (dan mengidentifikasinya) dengan memotongnya dengan cara yang sama. Jika ini bukan bola, ahli topologi telah menunjukkan bahwa ia harus berisi loop internal (loop yang tidak berpotongan satu sama lain) yang tidak dapat ditarik ke satu titik - seperti A dan B pada torus. Memotong permukaan di sepanjang salah satu loop ini menghilangkan beberapa sifat topologi yang menarik dari permukaan. Matematikawan telah menunjukkan bahwa untuk mengurangi permukaan menjadi poligon datar, perlu untuk memotongnya hingga beberapa kali.

Setelah menyederhanakan permukaan ke tingkat poligon, mudah untuk melihat bahwa jika kita merekatkan tepinya untuk mengembalikan permukaan asli, kita harus membuat torus, atau torus ganda, atau torus tripel, dll. Setelah semua, perekatan pertama akan mengubah poligon menjadi permukaan tampilan terowongan, dan masing-masing berikutnya akan menambah terowongan baru, atau hanya menjahit bagian yang terbuka. Ketika kami menyelesaikan proses, kami mendapatkan torus dengan beberapa lubang.

Pendekatan semacam itu tidak hanya menunjukkan kesetaraan topologi permukaan terhadap bola atau beberapa torus: pendekatan ini juga menyediakan cara untuk memberikan permukaan dengan struktur geometris yang sederhana dan seragam.

Bola, jelas, sudah memiliki struktur geometri yang seragam: geometrinya terlihat sama dari tempat mana pun di bola. Sebaliknya, permukaan donat sama sekali tidak seragam: wilayah tepi luar donat bengkok dengan cara yang mirip dengan bola, dan wilayah pada cincin bagian dalam ditekuk seperti pelana.

Dan tidak peduli bagaimana Anda menempatkan torus di ruang angkasa - tidak peduli bagaimana Anda meregangkan dan memelintirnya - Anda tidak dapat membuatnya sehingga geometrinya sama di tempat mana pun. Beberapa bagian akan bulat seperti bola, beberapa seperti pelana, beberapa mungkin datar.

Namun, dimungkinkan untuk melengkapi torus dengan struktur geometris abstrak yang identik pada titik mana pun - cukup nyatakan bahwa pada setiap bagian kecil torus, jarak dan sudut ditentukan dengan mengukur kuadrat dari mana, seperti yang telah kita lihat, torus dapat dibuat. Torus fisik dalam ruang biasa, panjang dan sudutnya yang sesuai dengan aturan abstrak ini, tidak dapat dibangun, tetapi definisi panjang dan sudut ini konsisten secara internal. Karena bujur sangkar memiliki geometri flat (Euclidean) yang biasa, kita katakan bahwa torus dapat dilengkapi dengan struktur Euclidean. Torus dengan geometri yang menyerupai permainan video di mana karakter menghilang dari sisi kiri layar dan muncul kembali di sebelah kanan, dan menghilang dari sisi atas, muncul di bagian bawah.

Mencoba melakukan operasi ini dengan torus ganda, kita akan menemui hambatan. Ingatlah bahwa kita dapat membuat torus ganda dengan menempelkan tepi oktagon. Jika kita menyatakan bahwa geometri torus ganda adalah untuk menyalin geometri oktagon, kita akan menghadapi masalah sudut-sudutnya. Setelah menempelkan oktagon ke dalam torus ganda, titik sudut akan direkatkan bersama, menjadi satu titik torus ganda. Akan ada delapan sudut pada titik ini, masing-masing akan menambah 135 derajat, yang bersama-sama akan menjadi 1080 derajat bukan 360.

Jika kita mencoba memberikan struktur geometris oktagon ke torus ganda, ternyata torus ganda kita akan memiliki geometri Euclidean biasa di mana-mana kecuali satu titik di mana permukaannya menjorok seperti topi runcing (titik sudut bukan masalah jika kita menempelkan persegi ke torus: kita merekatkan empat sudut kanan dan dapatkan 360 derajat sempurna).

Untuk mendapatkan struktur geometris yang halus pada titik sudut torus ganda, perlu bahwa masing-masing dari delapan sudut berkontribusi hanya 45 derajat, bukan 135. Sangat menarik bahwa oktagon seperti itu ada, tetapi tidak hidup dalam pesawat Euclidean biasa, tetapi pada struktur lain yang disebut cakram hiperbolik: yang ketiga sejenis geometri yang seragam dan konsisten secara internal, seperti bola atau Euclidean. Tetapi karena lebih sulit untuk membayangkan, itu ditemukan oleh ahli matematika hanya pada awal abad ke-19.

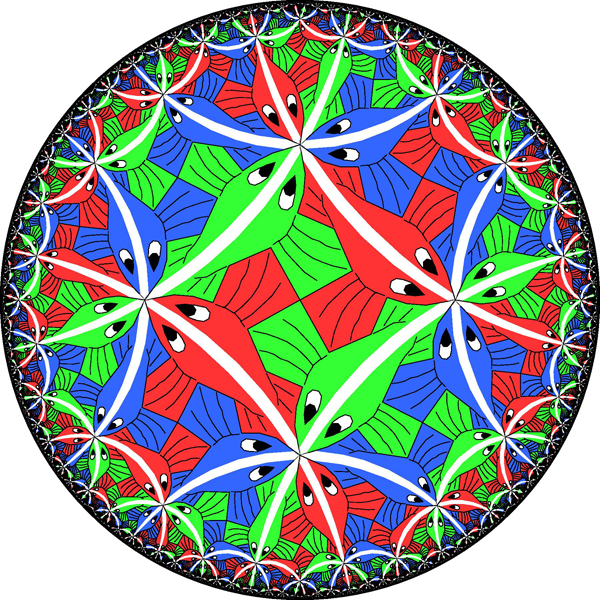Gbr.3

Secara kasar, geometri hiperbolik (atau geometri Lobachevsky) diperoleh jika kita menyatakan bahwa semua ikan pada Gambar. 3 memiliki ukuran yang sama. Orang dapat membayangkan bahwa Gambar. 3 sebenarnya adalah gambar disk yang diperoleh melalui lensa distorsi, yang membuat ikan lebih dekat ke tepi lebih kecil daripada ikan di tengah. Pada disk hiperbolik sejati di depan lensa, semua ikan memiliki ukuran yang sama.

Di ruang biasa, mustahil membuat cakram hiperbolik yang teratur dan halus sehingga semua ikan benar-benar sama. Tetapi dari sudut pandang abstrak, aturan ukuran ikan memberikan geometri yang konsisten secara internal dan terlihat sama pada titik mana pun - bukan untuk pengamat dengan lensa yang menyimpang, tetapi dari sudut pandang penduduk disk hiperbola.

Dalam geometri hiperbolik, jalur terpendek, atau "geodesik", antara dua titik adalah jalur melalui jumlah ikan sekecil mungkin. Path seperti itu selalu setengah lingkaran tegak lurus terhadap batas disk. Contohnya adalah setengah lingkaran berjalan di sepanjang duri ikan. Dari sudut pandang kami yang terdistorsi, jalur ini melengkung, tetapi bagi penduduk disk, ini adalah garis lurus. Seperti yang dikatakan Thurston, untuk menyetir, Anda tidak perlu memutar setir. Berbeda dengan bidang Euclidean, di mana garis-garis paralel selalu tetap pada jarak yang sama, pada cakram hiperbolik dua garis terputus-putus dapat dengan cepat berbeda satu sama lain.

Dari sudut pandang geometri hiperbolik, angka-angka pada Gambar. 4 adalah oktagon biasa dengan sisi lurus. Dalam salah satu octagons ini, semua sudut 45 derajat adalah apa yang kita butuhkan untuk torus ganda. Jika kita merekatkan sisi oktagon ini dengan benar, kita mendapatkan torus ganda dengan struktur hiperbolik yang ideal dan seragam.

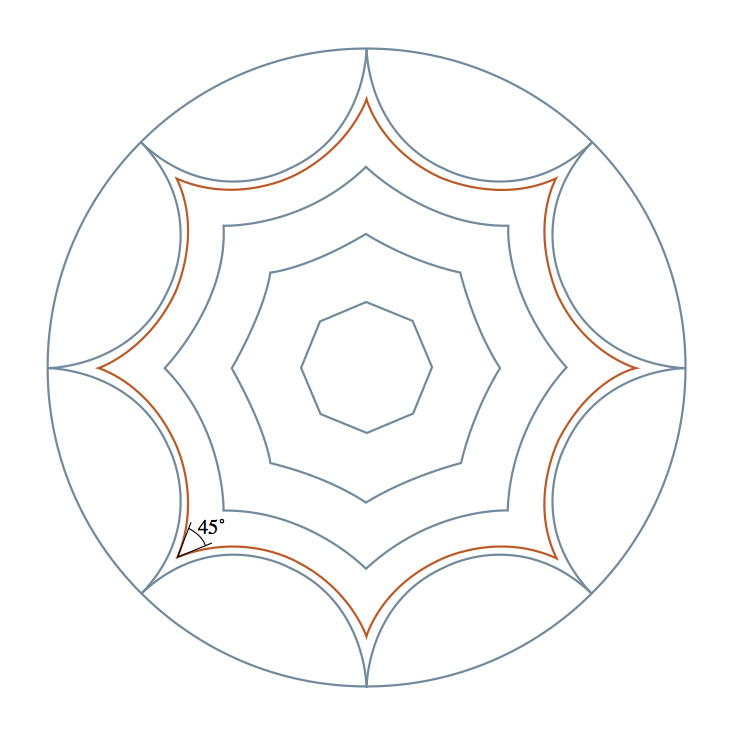Fig. 4

Dengan cara yang sama, kita dapat melengkapi torus rangkap tiga dengan struktur hiperbolik. Triple torus dapat dilem dari 12-gon, jadi jika kita membuat 12-gon hiperbolik dengan sudut internal 30 derajat, geometri hiperboliknya dapat ditransfer dengan lancar ke triple torus. Melanjutkan tema, kami dapat menyediakan torus dengan 4 lubang, dengan geometri hiperbolik ke-5 dan seterusnya. Klasifikasi permukaan kompak kami adalah sebagai berikut: satu permukaan dengan geometri bola (bola), satu dengan Euclidean (torus), dan banyak permukaan tanpa batas dengan geometri hiperbolik (semua tori dengan lebih dari satu lubang).

Selama seratus tahun terakhir, klasifikasi ini telah memberikan ahli matematika metode yang sangat bermanfaat untuk mentransfer pertanyaan topologi tentang permukaan ke domain geometris, dan sebaliknya. Klasifikasi permukaan adalah ide utama dalam studi bentuk dua dimensi, sebuah penemuan yang digunakan oleh semua penelitian lain sebagai titik awal.

Pengukuran selanjutnya

3-manifold jauh lebih beragam daripada 2-manifold, dan masalah dengan mereka lebih rumit. Bahkan pertanyaan yang tampak sederhana seperti dugaan Poincaré yang terkenal - yang menanyakan apakah versi tiga dimensi dari bola adalah satu-satunya bentuk tiga dimensi yang kompak di mana setiap loop dapat ditarik ke dalam satu titik tanpa menangkap lubang - tetap tidak terselesaikan selama hampir seratus tahun setelah dirumuskan oleh Henri Poincaré pada tahun 1904 tahun.

Namun Thurston dengan berani menyatakan bahwa dimungkinkan untuk membuat klasifikasi bentuk tiga dimensi yang mirip dengan klasifikasi dua dimensi yang ada.

Geometri Euclidean dua dimensi, bola, dan hiperbolik memiliki pasangan dalam tiga dimensi. Namun dalam tiga dimensi, daftar geometri "indah" tidak terbatas pada mereka. Ada geometri hibrid yang hiperbolik atau bulat dalam arah tertentu dan Euclidean pada yang lain. Secara umum, ada delapan jenis geometri dalam tiga dimensi, seragam dalam arti bahwa geometri terlihat sama di titik mana pun di ruang angkasa.

Thurston menyarankan bahwa, seperti halnya dengan permukaan, 3-manifold dapat dibandingkan dengan struktur geometris alami. Secara khusus, ia menyarankan bahwa jika Anda memotong 3-manifold kompak menjadi potongan-potongan dengan cara khusus, masing-masing potongan dapat dikaitkan dengan salah satu dari delapan geometri.

"Tujuannya adalah untuk sepenuhnya menyatukan topologi dan geometri dalam tiga dimensi," kata Minsky.

Pendekatan alami untuk "hipotesis geometriisasi" ini adalah untuk mencoba sesuatu yang mirip dengan apa yang kami lakukan dengan permukaan yang kami potong sepanjang kurva sampai mereka mengungkapkan semua sifat topologi yang menarik, dan sampai mereka disederhanakan menjadi poligon datar. Untuk 3-manifold, pendekatan yang sama akan memotongnya sepanjang permukaan sampai, mudah-mudahan, mereka menyederhanakan menjadi polyhedron, sisi yang berlawanan yang dapat direkatkan bersama untuk mendapatkan bentuk aslinya. Dan jika kita dapat membangun polyhedron ini menggunakan geometri yang benar, kita dapat mengubah geometri ini ke bentuk aslinya, seperti halnya dengan permukaan.

Ingat bahwa dalam kasus permukaan, setiap kurva harus memenuhi dua persyaratan: kurva tidak berpotongan dengan dirinya sendiri (ahli matematika mengatakan bahwa itu harus "tertanam"), dan itu harus, seperti yang kita sebut, menarik secara topologi, yaitu, mengelilingi beberapa detail topologi permukaan sehingga tidak dapat ditarik ke suatu titik (persyaratan ini memastikan bahwa memotong sepanjang kurva ini menyederhanakan topologi permukaan).

Pada tahun 1962, matematikawan Wolfgang Haken membuktikan bahwa 3-manifold dapat disederhanakan menjadi poligon jika 3-manifold berisi permukaan yang potongannya memenuhi dua syarat: harus tertanam dan “tidak dapat dikompres”, yaitu, setiap topologi menarik kurva pada permukaan juga akan menarik secara topologis dalam konteks yang lebih umum dari 3-lipatan sekitarnya.

Sebagai contoh, torus tidak akan dapat dimampatkan dalam ruang tiga dimensi biasa, karena loop yang melewati pembukaan torus secara topologi menarik dari sudut pandang permukaan torus, tetapi dalam ruang tiga dimensi dapat dikompresi menjadi satu titik. Sebaliknya, torus tidak dapat dimampatkan di dalam manifold 3, yang dapat diperoleh dengan mengentalkan permukaan torus sehingga tidak lagi tipis. Agar tidak dapat dimampatkan, setiap fitur topologi permukaan harus mencerminkan beberapa topologi internal berjenis 3. Sekarang manifold 3 yang memiliki permukaan yang tidak dapat dimampatkan disebut manifold Haken.

Jika 3-manifold kami memiliki permukaan built-in yang tidak dapat dimampatkan, maka memotongnya akan mengungkapkan beberapa topologi yang menarik dan memberi kami bermacam-macam yang disederhanakan. Selain itu, Haken menunjukkan bahwa jika manifold mengandung satu permukaan seperti itu, maka manifold baru yang diperoleh dengan memotong sepanjang itu juga akan menjadi manifold Haken: ia juga akan memiliki permukaan pemotongan built-in yang tidak dapat ditekan. Dan setelah sejumlah langkah yang terbatas, seperti yang ditunjukkan Haken, semua fitur topologi menarik dari manifold asli akan terputus, dan polyhedron sederhana akan tetap ada.

Pada akhir 1970-an, Thurston menunjukkan bahwa dimungkinkan untuk melengkapi polyhedron yang dihasilkan dengan salah satu dari delapan geometri delapan dimensi sedemikian rupa sehingga lancar mentransfer ke poligon yang baru direkatkan, cocok dengan sempurna di sudut dan tepi polyhedron. Dengan kata lain, Thurston membuktikan hipotesis geometriasinya untuk bermacam-macam manifold yang dekomposisi standarnya mengarah pada kepingan-kepingan yang merupakan manifold Haken.

Sayangnya, untuk manifold kompak 3-manifold, tidak ada jaminan bahwa ia memiliki permukaan seperti itu. Pada akhir 1970-an dan awal 1980-an, Thurston meyakinkan masyarakat bahwa manifold 3 yang berisi permukaan yang tidak dapat dimampatkan (manifold Haken) adalah pengecualian, bukan aturan.

Pencarian bukti hipotesis geometri untuk manifold selain manifold Haken telah menghentikan matematikawan selama lebih dari dua puluh tahun. Akhirnya, pada tahun 2002, Perelman menyajikan buktinya berdasarkan bidang matematika yang jauh dari yang dipelajari oleh sebagian besar pengikut Thurston. (Tampak seperti bukti Perelman menyentuh hipotesis seratus tahun Poincare juga, yang mengarahkan Clay's Mathematics Institute untuk menawarkan kepadanya hadiah jutaan dolar pada 2010 - yang ia tolak segera karena alasan rumit).

Bukti Perelman adalah titik balik, menggabungkan, seperti yang diimpikan Thurston, topologi dan geometri. Sekarang setiap masalah topologi yang terkait dengan 3-manifold memiliki pasangan geometris, dan sebaliknya. Tetapi teorema Perelman meninggalkan banyak pertanyaan penting yang belum terselesaikan tentang jenis manifold 3 apa yang bisa ada.

Dengan mengklasifikasikan manifold kompak (permukaan), matematikawan tidak hanya dapat menunjukkan bahwa setiap permukaan dapat dilengkapi dengan struktur geometris, tetapi juga membuat daftar lengkap dari semua manifold 2 yang mungkin. Dalam tiga dimensi, daftar seperti itu sangat kurang.

Tujuh dari delapan geometri tiga dimensi - semuanya kecuali hiperbolik - telah dikenal luas, dan bahkan sebelum karya Perelman, ahli topologi menyusun deskripsi lengkap tentang jenis manifold yang menerima salah satu dari tujuh geometri ini. Bentuk-bentuk ini relatif sederhana dan sedikit.

Tetapi, seperti dalam kasus permukaan, dalam tiga dimensi ternyata sebagian besar manifold adalah hiperbolik. Dan cakupan sejumlah besar kemungkinan 3-manifold hiperbolik jauh lebih buruk di antara matematikawan daripada tujuh geometri lainnya.

"Dari delapan jenis geometri, manifold hiperbolik adalah yang paling misterius dan terkaya," kata Nicolas Bergeron dari Universitas Pierre dan Marie Curie di Paris.

Hasil Perelman mengatakan kepada ahli matematika bahwa manifold hiperbolik adalah perbatasan terakhir - satu-satunya jenis manifold 3 yang masih harus dipahami. Tetapi dia tidak memberi tahu mereka seperti apa bentuk-bentuk hiperbolik ini.

Cerita sampul

Sekali lagi, matematikawan dapat beralih ke pekerjaan Thurston untuk bimbingan. Daftar pertanyaannya yang terkenal berisi banyak hipotesis tentang sifat-sifat manifold-hiperbolik 3, yang mencakup dua hipotesis yang secara langsung berkaitan dengan penampilan mereka: "hipotesis virtual Haken" dan hipotesis "bundel virtual".

Hipotesis virtual Haken (HHC) menyatakan bahwa setiap manifold hiperbolik 3-manifold hampir menjadi manifold Haken dalam arti tertentu: dimungkinkan untuk mengubah manifold menjadi manifold Haken dengan memperluas jumlah terbatasnya kali dengan cara tertentu. Manifold baru yang tidak dilipat ini disebut "penutup terbatas" dari manifold asli.

Matematikawan mengatakan bahwa satu varietas N mencakup varietas lain M, jika, secara kasar, memungkinkan untuk membungkus N di sekitar M beberapa kali (mungkin tak terbatas) sehingga setiap bagian M tertutupi sebanyak yang lainnya. Untuk menjadi penutup, bungkus ini harus memiliki banyak properti lain - misalnya, N tidak boleh membungkuk ke dirinya sendiri, atau merobek selama bungkus. Setiap potongan M ditutupi dengan banyak salinan identik dalam N. yang meliputinya.Gambar.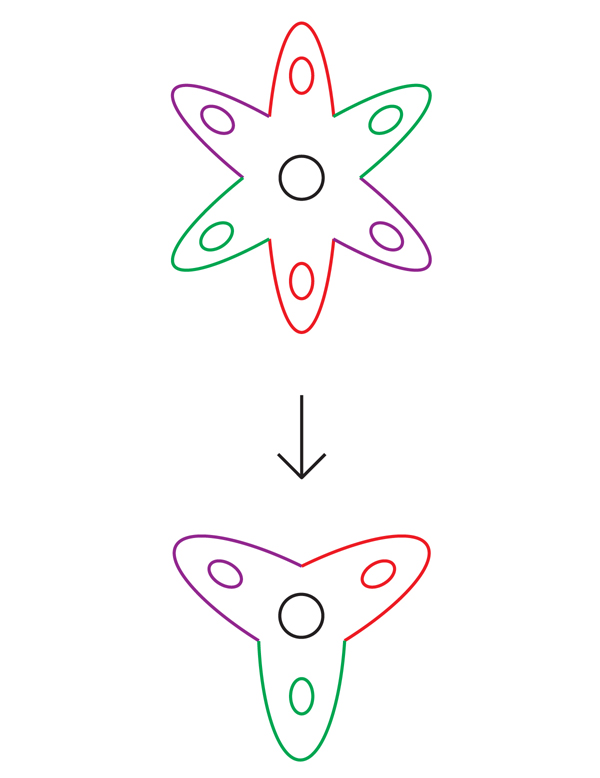

5

Misalnya, bunga enam kelopak pada Gambar. 5 mencakup bunga tiga kelopak: cukup bungkus bunga enam kelopak dua kali sekitar tiga kelopak. Setiap titik warna tiga-kelopak ditutupi dengan dua titik enam-kelopak. Matematikawan menyebut ini lapisan dua lapis.

Dengan cara yang sama, sebuah silinder infinite menutupi torus: cukup putar silinder di sekeliling torus beberapa kali tanpa batas (Gbr. 6). Setiap titik silinder tertutup: loop A ditutupi oleh satu set loop tak terbatas yang terdistribusi secara merata di atas silinder, dan loop B ditempatkan pada silinder dalam garis yang membentang.

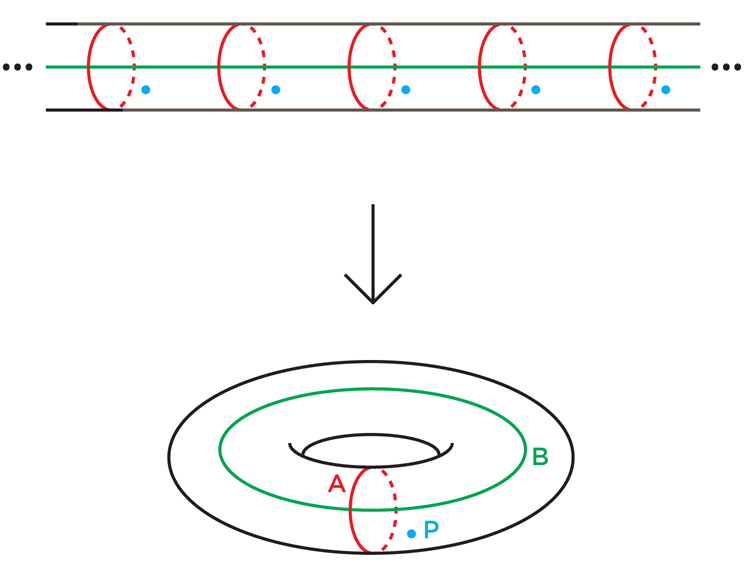Fig. 6

Topologi keanekaragaman dan penutupnya terkait erat. Untuk membuat ulang bermacam-macam lapisan n-layer, Anda hanya perlu melipatnya sendiri n kali. Dan sebaliknya, untuk membuat ulang lapisan berdasarkan varietas, Anda memotongnya, membuat salinan, dan menempelkannya di sepanjang perbatasan (lapisan beton yang Anda terima tergantung pada pilihan urutan pengeleman).

Penutup mempertahankan beberapa sifat topologi dari bermacam-macam, dan mengungkapkan yang lainnya. Silinder infinite, misalnya, ingat bahwa loop A pada torus ditutup, tetapi lupa bahwa loop B juga tertutup.

Proses penyebaran ini mendorong Thurston dengan harapan bahwa untuk 3-manifold adalah mungkin untuk menutup dengan sejumlah lapisan yang terbatas, yang akan menjadi manifold Haken. Kami telah menunjukkan bahwa seseorang seharusnya tidak mengharapkan bahwa manifold-kompak hiperbolik 3-manifold akan menjadi manifold Haken (bahwa ia akan memiliki permukaan built-in yang tidak dapat dimampatkan). Tetapi pada tahun 1968, matematikawan Jerman, Friedhelm Waldhausen, menyarankan bahwa manifold semacam itu setidaknya harus mengandung permukaan yang tidak dapat dimampatkan, meskipun ia dapat melewati dirinya sendiri dan tidak tertanam.

Jika demikian, Thurston berpendapat, mungkin ada lapisan akhir di mana permukaan terbuka dengan cara yang menghilangkan semua persimpangan diri. Lapisan jadi sering disederhanakan dengan cara ini. Misalnya, karena kurva pada bunga tiga kelopak pada Gambar. 7 mengelilingi lubang pusat dua kali, tidak ada peregangan dan pergeseran yang dapat menyebabkannya tidak bersinggungan dengan dirinya sendiri. Tetapi jika kita mengubah kurva ini pada bunga enam kelopak, mulai dari titik P tertentu, kurva merah yang dihasilkan (yang oleh ahli matematika disebut "naik" dari kurva asli) akan mengelilingi lubang pusat hanya sekali dan tidak akan berpotongan dengan dirinya sendiri. (Ada juga kenaikan kedua, kurva biru melintasi merah di dua titik, menutup titik persimpangan di bunga tiga kelopak).

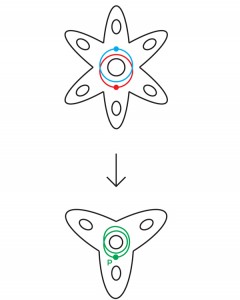Gbr. 7

Dalam sebuah makalah tahun 1982, Thurston menyarankan bahwa jika kita memiliki manifold hiperbolik 3-kompak, harus ada cara untuk mengembangkannya sehingga kita telah menanamkan permukaan pada penutup yang terbatas - yaitu, manifold-3 harus “hampir Haken”.

Seperti yang telah kita lihat, manifold Haken dapat dibangun dengan menempelkan batas-batas wajah polihedron dengan cara tertentu. VGH menyiratkan bahwa manifold 3-lipatan hiperbolik apa pun dapat dibangun dengan terlebih dahulu menempelkan polyhedron dengan benar, dan kemudian membungkus bentuk yang dihasilkan di sekitar itu sendiri beberapa kali.

Thurston bahkan membuat asumsi yang lebih keras: bahwa setiap manifold 3-hiperbol kompak dapat dikelompokkan, yaitu, memiliki penutup berlapis yang terbatas. Variasi yang "bertingkat atas sebuah lingkaran" (seperti yang dikatakan oleh ahli matematika) dibangun dengan sedikit menebal permukaan, yang membuatnya tiga dimensi, dan menempelkan batas dalam dan luar bersama-sama dengan cara apa pun yang memastikan koneksi permukaan yang mulus di setiap titik. (Perekatan seperti itu tidak mungkin dilakukan di ruang biasa tanpa persimpangan bagian-bagian yang berlipat ganda satu sama lain, tetapi secara abstrak masih dapat dipelajari). Stratifikasi dari manifold dikatakan, karena dimungkinkan untuk membayangkan bagaimana permukaan yang menebal diregangkan sehingga permukaan batas berbeda satu sama lain,dan kemudian buka dan tarik ke arah satu sama lain sebelum menempel, dan variasi yang dihasilkan menyerupai gelang dengan manik-manik yang sangat tipis dalam bentuk permukaan di setiap titik benang gelang. Manik-manik ini berlapis-lapis.

Setiap manifold berlapis adalah manifold Haken, tetapi tidak sebaliknya. Oleh karena itu, hipotesis bundel virtual lebih kuat daripada VGH, dan Thurston tidak yakin itu benar. "Pertanyaan yang dipertanyakan ini, tampaknya, memiliki peluang pasti untuk mendapatkan jawaban positif," adalah semua yang bisa ia tulis dalam sebuah karya 1982.

Thurston awalnya menyatakan VGH dalam upaya awal untuk mendekati hipotesis geometriasinya, yang telah dia buktikan untuk Haken 3-manifold. Jika VGH benar, dan masing-masing manifold 3-kompak adalah penutup Haken, maka mungkin (Thurston berharap) akan mungkin untuk menggunakan struktur penutup geometris untuk membangun struktur geometris dari manifold asli.

30 tahun kemudian, jauh lebih lambat daripada Perelman membuktikan hipotesis geometriisasi dengan metode yang sama sekali berbeda, VGH dan hipotesis bundel virtual tetap tidak terbukti. Mereka, bersama dengan dua hipotesis lain yang terkait dengannya, tetap menjadi satu-satunya pertanyaan yang tidak terjawab dari 23. Perhitungan komputer berbicara dalam mendukung validitas VGH - penutup Haken yang terbatas ditemukan untuk masing-masing dari 10.000 manifold 3-hiperbola yang dipilih komputer. Pekerjaan ini dilakukan oleh Thurston dan Nathan Dunfield dari University of Illinois di Urbana-Champaign. Tetapi penghancuran komputer bukanlah bukti.

“Ketika Thurston mengajukan hipotesis Haken virtual ini, pertanyaan ini tampak mudah. Tetapi dia dengan keras kepala menentang keputusan itu, yang menjelaskan betapa sedikitnya yang kita pahami di bidang ini, kata Minsky. "Ternyata ketidaktahuan kita dalam arah ini sangat dalam."

Permukaan bangunan

Pada tahun 2009, air keruh yang mengelilingi penyimpanan air-air mulai dimurnikan. Tahun itu, Markovich dan Jeremy Kahn, yang saat itu bekerja di Stony Brook University, mengumumkan bukti langkah kunci menuju pembuktian VHC. Hasilnya, yang akan kita sebut "teorema pada permukaan yang tidak dapat dimampatkan," mendalilkan bahwa setiap manifold hiperbolik 3-manifold berisi permukaan yang tidak dapat dimampatkan (yang, mungkin, berpotongan dengan dirinya sendiri, dan tidak tertanam).

Bukti Kan dan Markovich adalah salah satu contoh sentral dari interaksi topologi tiga dimensi dan geometri: teorema pada permukaan yang tidak dapat dimampatkan adalah pernyataan topologi murni, tetapi Kan dan Markovich secara aktif menggunakan struktur lain yang diambil dari geometri hiperbolik untuk membuktikannya.

Untuk membangun permukaan di dalam 3-manifold, Kahn dan Markovich menggunakan properti bentuk hiperbolik yang disebut "pencampuran eksponensial". Ini berarti bahwa jika Anda memulai jalur di suatu tempat di area kecil di dalam manifold, pilih arah, dan bayangkan bahwa area Anda mulai bergerak di sepanjang sungai yang mengalir di sekitar arah yang dipilih, maka area Anda secara bertahap akan menyebar dan membungkus manifold 3, itu akan mendapatkan ke tempat yang memungkinkan dari segala arah yang memungkinkan. Selain itu, ia akan melakukannya dengan sangat cepat dalam arti "eksponensial" yang tepat.

Properti pencampuran adalah unik untuk manifold-3 hiperbolik dan tumbuh, secara kasar, dari fakta bahwa, berbeda dengan ruang Euclidean, dalam ruang hiperbolik “garis lurus” atau geodesi dibengkokkan relatif satu sama lain. Jika Anda memilih area kecil dari disk hiperbola dan membiarkannya bergerak ke arah yang dipilih, itu akan tumbuh secara eksponensial dengan cepat. Di dalam manifold 3-kompak, wilayah yang tumbuh juga akan tumbuh secara eksponensial, tetapi karena ukuran manifold terbatas, wilayah ini pada akhirnya akan membungkusnya berulang kali, tumpang tindih sendiri berkali-kali. Selain itu - dan ini sudah lebih sulit untuk dibuktikan - area akan membungkus manifold secara merata, melewati semua titik dengan frekuensi yang kira-kira sama.

Matematikawan berurusan dengan sifat pencampuran eksponensial ini lebih dari 25 tahun yang lalu dan dengan hati-hati mempelajari statistik "aliran geodesi" ini, setelah mengetahui kapan dan seberapa sering suatu area tertentu akan melewati pada titik tertentu. Tetapi sampai Kahn dan Markovich menggunakan teorema permukaan yang tidak dapat dimampatkan dengan benar, matematikawan tidak dapat menggunakan properti ini untuk membangun struktur topologi dalam bermacam-macam (Ahli matematika lain, Lewis Bowen dari Universitas A&M Texas, mencoba menggunakan pencampuran eksponensial untuk membangun permukaan yang tidak dapat dimampatkan di manifold 3, tetapi karyanya menemukan kendala teknis).

Untuk melihat bagaimana properti pencampuran eksponensial membantu membangun struktur topologi dan geometris, kami menerapkannya pada tugas yang lebih sederhana daripada membangun permukaan: membangun loop geodesik tertutup yang panjangnya dekat dengan angka besar favorit kami (kami menyatakannya dengan R).

Untuk membuat loop, kami memilih titik awal di manifold dan arah awal apa pun, dan kemudian menghidupkan selang air imajiner yang terletak di area kecil termasuk titik awal dan mengarahkannya secara kasar ke arah yang dipilih. Tetesan air akan terbang di sepanjang jalur geodesik, dan selama R cukup besar, pencampuran aliran akan berarti bahwa pada saat tetesan telah melewati jarak R, mereka akan didistribusikan secara merata di seluruh varietas. Secara khusus, setidaknya satu tetes harus kembali ke area titik awal. Kemudian kita hanya membangun sebuah jembatan kecil yang menghubungkan geodesik dari drop ini ke titik awal untuk mendapatkan loop yang hampir sempurna geodesic dengan panjang sekitar R. Sangat mudah untuk menunjukkan bahwa dengan mengencangkan loop ini lebih ketat pada manifold,Anda bisa mendapatkan loop geodesik yang sempurna.

Perhatikan bahwa metode ini memberi kami lebih dari satu loop geodesik dekat dengan R. Dalam proses ini, Anda dapat menggunakan titik awal dan arah apa pun, sehingga Anda dapat membuat banyak loop seperti itu. Ini adalah prinsip dasar untuk membangun struktur menggunakan pencampuran eksponensial.

Pencampuran eksponensial “mengklaim bahwa apa pun struktur dalam keanekaragaman yang Anda temukan, Anda akan menemukannya dalam jumlah yang cukup,” kata Kalegari.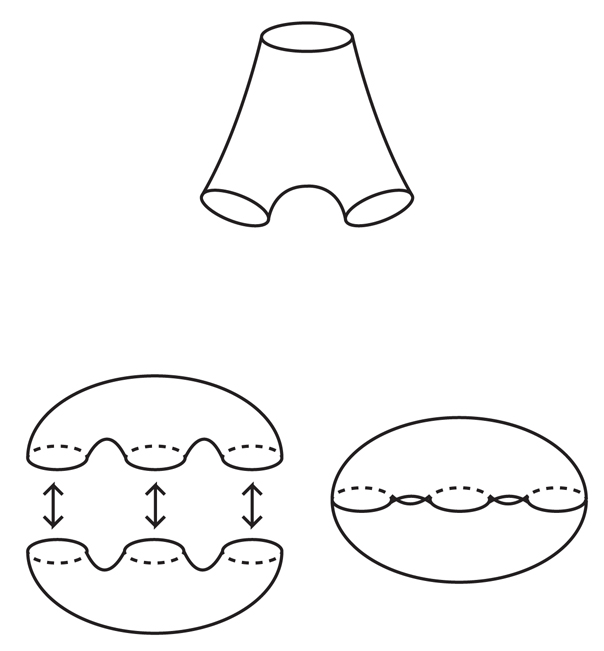

Gbr. 8

Kan dan Markovich menggunakan pendekatan yang mirip dengan latihan kami untuk membuat "pasang celana" - permukaan yang secara topologi setara dengan bola dengan tiga lubang (bisa dikatakan, satu untuk sabuk dan dua untuk kaki). Celana ini adalah bahan awal untuk membangun semua permukaan yang ringkas, kecuali untuk bola dan torus - misalnya, menempelkan (atau menjahit) dua celana memberi kita torus ganda (Gbr. 8).

Kan dan Markovich menunjukkan bahwa untuk jumlah R yang cukup besar dimungkinkan untuk membuat banyak pasangan celana dalam manifold, bahwa tiga "manset" mereka akan mendekati panjang R, dan akan hampir sepenuhnya geodesik, yaitu, setiap bagian dari permukaan celana akan terlihat hampir sama dari titik tersebut. pandangan geometri hiperbolik.

Mereka juga menunjukkan bahwa untuk manset apa pun, celana panjang memiliki sepasang celana panjang lain, yang keluar dari manset dengan arah yang berlawanan. Menjahit celana ini bersama di borgol, Kahn dan Markovic menerima keluarga besar permukaan kompak, hampir sepenuhnya geodesik, dengan kerutan kecil di jahitannya. Hampir permukaan geodesik tidak dapat dimampatkan di dalam manifold 3-nya, oleh karena itu, konstruksi Kan dan Markovich membuktikan teorema permukaan yang tidak dapat dimampatkan.

Metode ini juga menunjukkan bahwa manifold-3 tidak hanya memiliki satu permukaan yang tidak dapat dimampatkan, tetapi "sebuah struktur kaya permukaan yang hampir geodesik di tempat yang berbeda," kata Kalegari.

Karya Kahn dan Markovich memberi mereka Penghargaan Clay Institute of Mathematics 2012, yang diberikan untuk terobosan matematika.

"Teknik Kahn dan Markovich tidak kalah dengan minat pada hasil mereka, dan karya ini pasti akan menginspirasi banyak bidang penelitian lain yang terkait dengannya," prediksi Jeffrey Brock dari Brown University dalam artikel 2011.

Struktur tersembunyi

Kan dan Markovich menciptakan titik awal bagi matematikawan yang berusaha membuktikan VHC.

Mereka menunjukkan bahwa setiap manifold dijamin mengandung permukaan yang tidak dapat dimampatkan. Tetapi permukaan ini dapat melewati dirinya sendiri, mungkin di banyak tempat, dan tidak tertanam. Untuk mendapatkan VGHYU berdasarkan karya Kan dan Markovich, matematikawan perlu menemukan sampul yang terbatas dari manifold, di mana, persis seperti dalam contoh dengan enam dan tiga warna yang dilambangkan, permukaan naik ke satu set permukaan yang tidak berpotongan (meskipun mereka dapat berpotongan satu sama lain). Jika memungkinkan, masing-masing dari mereka akan menjadi permukaan yang tidak bisa dimampatkan dalam lapisan, yang berarti bahwa lapisan itu adalah Haken.

Tetapi bagaimana menemukan liputan seperti itu?

"Ada kesenjangan besar antara karya Kahn dan Markovic dan WHC," kata Danfield. "Penemuan mereka penting, tetapi tidak jelas apakah itu akan membantu dalam mencari permukaan yang tertanam."

Karya Kahn dan Markovich menarik perhatian Daniel Wise dari Universitas McGill. Wise membuat karir dalam penelitian tentang penghapusan persimpangan diri dari objek topologis menggunakan penutup yang terbatas, tetapi ia bekerja dalam konteks "kompleks kubik", objek yang pada pandangan pertama sangat berbeda dari manifold 3. Karya Kahn dan Markovich membantu Wise menunjukkan kepada matematikawan lain bahwa kedua konteks ini tidak begitu berbeda.

Kompleks kubik - itu adalah kompleks kubik (CC): itu adalah seperangkat kubus, tidak hanya kubus tiga dimensi disebut "kubus" di sana, tetapi juga bentuk dalam sejumlah dimensi, terdiri dari semua titik yang koordinatnya terletak, misalnya, pada interval antara - 1 dan +1. Misalnya, persegi adalah kubus dua dimensi, dan segmen adalah satu dimensi. Kubus di pesawat ruang angkasa terhubung satu sama lain di sepanjang sudut, tepi, wajah dan sisi dimensi yang lebih tinggi.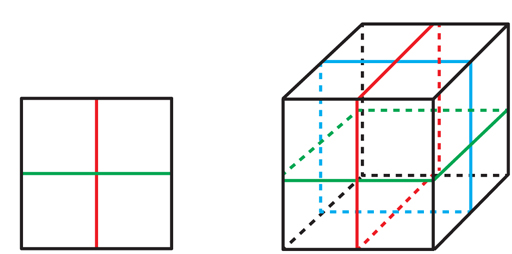

Gambar. 9

CC sangat berbeda dari 3-manifold - mereka bahkan tidak berjenis, karena persimpangan dua kubus dimensi yang berbeda tidak menyerupai ruang biasa dari salah satu dimensi. Tapi CC adalah objek yang disederhanakan di mana satu aspek kunci dari permukaan yang terkandung dalam 3-manifold dipelajari: fakta bahwa permukaan seperti itu setidaknya secara lokal membagi lingkungannya menjadi dua bagian.

Jika Anda perlu menjelajahi objek yang membagi bentuk menjadi dua bagian, kubus adalah bidang alami untuk memulai, karena semua bentuk yang mungkin, mereka memiliki objek yang paling sederhana: hyperplanes yang memotongnya di tengah. Alun-alun memiliki dua hyperplanes (GP) - garis vertikal dan horizontal, memotongnya menjadi dua. Kubus memiliki tiga dokter (lihat Gambar 9). Sebuah kubus n-dimensi memiliki n GP berpotongan di pusatnya.

"Hyperplanes mirip dengan permukaan dalam manifold 3, tetapi Anda melihatnya secara instan," kata Wise. "Sulit untuk mencari permukaan, tetapi hyperplanes tersedia untuk Anda sejak awal."

Jika kita mulai dengan seorang dokter di dalam sebuah kubus di sebuah QC, maka ada tepat satu cara untuk memperluas seorang dokter ke seorang dokter di kubus tetangga; setelah itu, hanya ada satu cara untuk memperluas mereka ke yang tetangga; dan sebagainya. Oleh karena itu, untuk setiap dokter umum di CC ada cara unik untuk mengembangkannya ke dokter di seluruh CC (lihat Gambar 10).

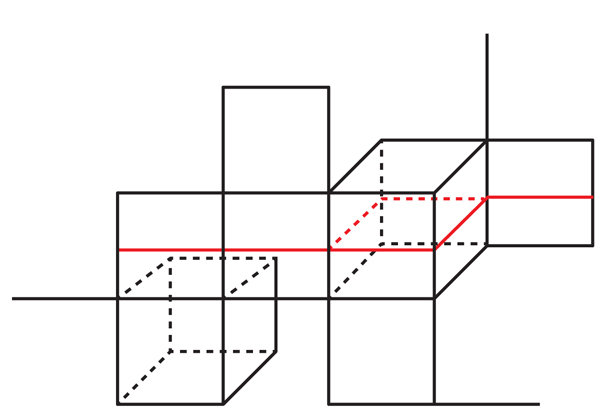Gbr. 10. Hyperplane merah di alun-alun paling kanan secara unik mengembang ke hyperplane di seluruh kompleks kubik.

Kualitas ini sangat kontras dengan 3-manifold, di mana area permukaan kecil dapat diperluas ke seluruh permukaan dengan berbagai cara. CC dengan dokter mereka "cantik, sejernih kristal, dan ketat," kata Eigol, dan mereka tidak memiliki "kelemahan" lipatan 3-manifold dan permukaannya.

Ketika kita memperluas GP di pesawat ruang angkasa, itu dapat menemukan kubus dari mana semuanya dimulai dan melewati itu tegak lurus ke GP awal (lihat Gambar. 11). Dengan kata lain, GPU yang diperluas tidak harus built-in. Seperti halnya dengan permukaan di dalam manifold 3, orang dapat bertanya apakah QC memiliki penutup yang terbatas di mana dokter berpotongan diri ini naik menjadi tertanam - ini adalah versi dari hipotesis virtual Haken untuk QC.

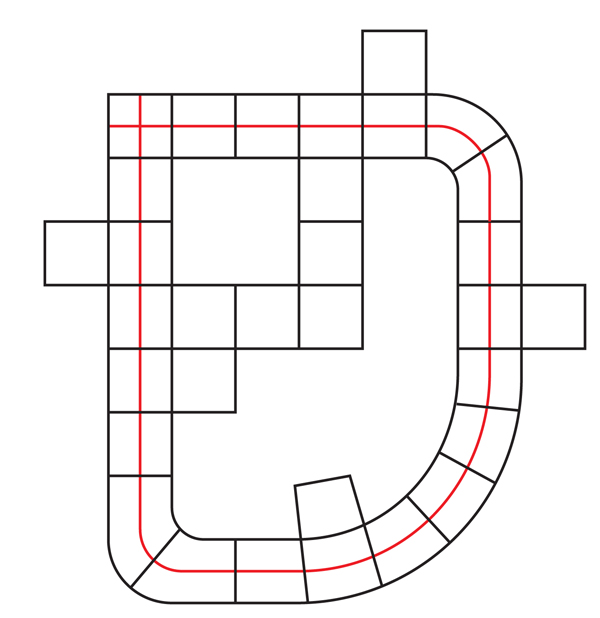Gbr.11

Beberapa tahun yang lalu, Wise dan Frédéric Haglund dari University of Paris-South XI mengidentifikasi kelas "khusus" QC yang, di samping properti lainnya, hanya memiliki GPU bawaan. Dalam dekade terakhir, Wise telah mengembangkan gudang teknik yang diadaptasi untuk mengidentifikasi "QC khusus." Pada tahun 2009, Wise merilis "pekerjaan inti," setebal 200 halaman, seperti yang dikatakan Danfield, di mana ia menggambarkan serangkaian penemuan terkait dengan QC khusus, seperti "teorema kombinasi," yang menunjukkan cara mengumpulkan QC khusus untuk menjamin QC baru, juga memiliki "spesialisasi". Dalam karyanya, Wise merumuskan hipotesis yang menyatakan, secara kasar, bahwa setiap QC dengan geometri yang menekuk dengan cara yang mirip dengan geometri hiperbolik adalah "hampir" istimewa - artinya, ia memiliki penutup terbatas yang khusus. Hipotesis ini disebut hipotesis Bijaksana.

Wise yakin bahwa jika bentuk ini dalam beberapa cara mirip dengan QC - ketika itu dapat "dipotong dadu" - maka struktur QC akan menjadi kunci untuk menemukan banyak properti dari bentuk aslinya.

"CC adalah rahasia yang bahkan orang tidak tahu harus bertanya apa," katanya. "Ini adalah struktur tersembunyi yang mendasar."

Hutan kubik

Weise sangat khawatir tentang bentuk kubus, tetapi pada awalnya rekan-rekannya menertawakannya karena mania ini.

Kemudian Kahn dan Markovich membuktikan teorema permukaan yang tidak dapat dikompres, dan Wise dan Bergeron segera menerbitkan sebuah makalah yang menunjukkan bahwa keberadaan permukaan yang tidak dapat dikompres dalam manifold 3-lipatan hiperbolik memberikan metode untuk memotongnya - dan agar permukaan 3-manifold sesuai dengan hyperplanes di kompleks kubik yang dihasilkan .

Kunci dari desain Wise dan Bergeron adalah fakta bahwa Kahn dan Markovich menunjukkan bagaimana membangun bukan hanya satu, tetapi banyak permukaan. Mengikuti pendekatan cubing, pertama kali dirumuskan pada tahun 2003 oleh Michael Sageev, sekarang bekerja di Technion (Israel), Wise dan Bergeron mulai dengan mengambil koleksi besar permukaan Kahn-Markovich - cukup untuk membagi 3-manifold menjadi poligon kompak.

Sekarang bayangkan salah satu titik persimpangan dari permukaan ini - misalnya, ada n permukaan di dalamnya. Dugaan Sageev adalah untuk menganggap persimpangan ini sebagai bayangan, dengan kata lain, dari persimpangan n hyperplanes dalam kubus n-dimensi. KK yang sesuai dengan manifold 3 dibangun, secara kasar, dengan menambahkan satu kubus n-dimensi untuk setiap persimpangan permukaan n (pada kenyataannya, semua ini dibangun lebih halus untuk memperhitungkan berbagai keadaan topologi yang tidak terduga). Dua kubus dalam kompleks berbatasan jika titik-titik perpotongan yang sesuai dalam manifold-3 dihubungkan oleh permukaan salah satu polytopes.

"Kompleks kubik diperlukan untuk secara akurat menghitung bagaimana permukaan saling bersilangan dan dengan satu sama lain," kata Danfield.

Wise dan Bergeron menunjukkan bahwa KK ini "setara secara homotopik" dengan manifold aslinya, yaitu, KK dapat dikompresi dan diregangkan (dengan mempertimbangkan perataan dalam beberapa dimensi dan proses terbalik) hingga KK berubah menjadi manifold, dan sebaliknya. Selain itu, kesetaraan homotopik ini mengubah setiap permukaan 3-manifold menjadi GP ekuivalen homotopy yang sesuai pada KK.

QC yang dibangun dengan cara ini memenuhi persyaratan geometrik hipotesis Wise, yang berarti bahwa jika hipotesis Wise benar, maka QC ini memiliki cakupan terbatas di mana semua dokter akan tertanam.

Jika pelapisan terbatas seperti itu benar-benar ada (misalnya, yang menutupi lembaran m), maka kita perlu ingat bahwa pelapisan itu dapat dibangun dari QC itu sendiri, memotongnya dengan cara khusus, kemudian membuat salinan dari QC ini dan menempelkannya bersama di sepanjang garis potong. Mudah untuk menunjukkan bahwa resep untuk pembuatan lapisan ini dapat ditransfer ke pembuatan penutup akhir dari 3-manifold, dan bahwa dalam tugas akhir ini meliputi permukaan Kan-Markovich yang digunakan untuk membangun CC akan naik ke permukaan yang tertanam. Dengan kata lain, jika hipotesis Wise benar, maka IHC juga benar.

"Ini adalah kompromi yang sangat aneh: QC Anda mungkin, misalnya, 10.000 dimensi, dan mungkin bagi Anda tampaknya dalam beberapa hal Anda memperburuk situasi," kata Wise. "Tetapi meskipun memiliki nilai QC, banyak propertinya sangat mudah dimengerti, jadi prosedur ini sangat berharga." "Kami lebih suka sesuatu yang besar, tetapi terorganisir dengan baik, daripada 3-manifold."

Bahkan setelah Wise dan Bergeron menjalin hubungan antara QC dan VGH, kebanyakan ahli topologi yang mempelajari manifold 3 menjauh dari QC. Mungkin karena 200 halaman karya Wise mengecewakan, atau karena CC sangat berbeda dari tempat biasanya.

"Gagasan ini terlalu esoteris bagi orang yang muncul dari geometri hiperbolik," kata Bergeron.

Tetapi seorang ahli matematika sudah berpengalaman dalam topologi 3-manifold, serta dalam hal-hal kombinatorial yang lebih abstrak yang Wise gunakan dalam pendekatannya.

"Saya pikir Jan Eigol adalah satu-satunya spesialis 3-manifold yang mengerti cukup awal bagaimana ide-ide Wise dapat digunakan untuk topologi 3-manifold," kata Bergeron.

Eigol masuk lebih dalam ke dalam studi tentang "pekerjaan utama" Bijaksana dan menjadi yakin bahwa semua bagian yang terkait dengan hipotesis Bijaksana adalah benar. Aigol telah terlibat dalam VHC selama beberapa waktu; dia menyadari bahwa pendekatan Wise, mengubah permukaan yang lembek menjadi hyperplanes kristal, adalah persis apa yang dia butuhkan.

“KK memberi kita hutan untuk pembangunan lapisan akhir,” katanya.

Untuk membangun lapisan akhir khusus pada pesawat ruang angkasa Wise-Bergeron, Aigol mulai memotong pesawat ruang angkasa di sepanjang GP menjadi "Lego cubes". Dia kemudian memberikan warna pada wajah balok, sehingga setiap dua wajah yang ditemukan di sudut memiliki warna yang berbeda. Kemudian, Eigol menunjukkan bahwa, secara kasar, ada cara untuk merekatkan sejumlah terbatas Lego cubes di sepanjang wajah dengan warna yang sama sedemikian rupa sehingga warna di sisi wajah-wajah ini juga akan cocok. Akibatnya, setiap GP yang diperpanjang akan memiliki warna yang sama. QC yang dihasilkan akan menjadi lapisan akhir dari aslinya, dan semua dokternya akan tertanam, karena dua dokter yang berpotongan akan memiliki warna yang berbeda, jadi ini tidak akan menjadi satu GP yang berpotongan itu sendiri.

Pada 12 Maret, Aigol mengumumkan bukti hipotesis Bijaksana, dan karenanya hipotesis virtual Haken.

"Itu adalah berita paling menarik sejak Perelman membuktikan hipotesis geometriisasi," kata Danfield.

Informasi melewati sebuah komunitas peneliti dari 3-manifold, dan QC segera menjadi topik umum untuk semua ahli topologi.

"Saya pikir sejauh ini komunitas matematika belum memahami seberapa kuat pekerjaan Wise," kata Aigol. "Saya pikir hasil saya akan menjelaskan kepada orang-orang apa kemajuan luar biasa yang telah ia buat."

Sekarang, menurut Wise, matematikawan mulai menyadari bahwa "setiap kali Anda menghitung sesuatu, Anda dapat mengungkapkan segala macam rahasia struktur."

Akhir zaman

Bukti Aigol tentang teori Wise adalah bukti "4 untuk harga 1": itu membuktikan tidak hanya VGH, tetapi juga tiga lainnya dari 23 pertanyaan Thurston, yang sampai saat itu tetap terbuka. Pada saat menjelang pembuktian, Eigol dan matematikawan lainnya menunjukkan bahwa ketiga pertanyaan ini - hipotesis bundel maya dan dua pertanyaan teknis lainnya tentang manifold 3 hiperbolik - juga diikuti dari hipotesis Wise.

Dalam kasus hipotesis bundel maya, kita ingat bahwa tujuannya adalah untuk menunjukkan bahwa setiap manifold hiperbolik 3-manifold kompak memiliki penutup hingga yang disatukan dalam sebuah lingkaran, yaitu, dibangun dengan menempelkan bagian-bagian berlawanan dari permukaan yang menebal. Dari VGH kita tahu bahwa manifold memiliki lapisan Hakenov yang terbatas - yaitu, lapisan tersebut memiliki permukaan yang tidak dapat dimampatkan yang terpasang. Jika Anda membuka bermacam-macam Haken di sepanjang permukaan ini, Anda akan mendapatkan sesuatu yang tampak seperti permukaan yang menebal di ujungnya, tetapi karena Tuhan tahu apa yang ada di "nyali".

Yang Aigol dalam perjalanan baru-baru ini ke Daejeon, Korea Selatan.

Pada tahun 2008, menurut Kalegari, ada "terobosan mengejutkan" ketika Eigol menunjukkan bahwa hiperbolik 3-manifold yang memenuhi kondisi teknis khusus dijamin hampir terstratifikasi. Tahun berikutnya, Bijaksana atas dasar ini menunjukkan bahwa semua manifold Haken secara virtual bertingkat. Artinya, ada cara untuk memperluas manifold Haken untuk mendapatkan penutup yang terbatas yang mengungkapkan topologi yang kompleks dan mengarah ke manifold foliated sederhana. Oleh karena itu, jika bermacam-macamnya adalah Hakenov, itu harus secara virtual bertingkat.

"Saya pikir semua orang percaya bahwa VGH akan benar, tetapi hipotesis bundel virtual tampaknya kurang dapat diakses oleh kami," kata Kalegari. "Bagi saya, fakta bahwa hipotesis stratifikasi virtual mengikuti dari VGH adalah salah satu sisi paling mengejutkan dari keseluruhan cerita ini."

Dengan bukti hipotesis bundel virtual, "Anda dapat tergoda dan memutuskan bahwa manifold 3 terlalu sederhana karena manifold yang dikelompokkan dalam lingkaran itu sederhana," kata Minsky. "Tapi saya pikir ini mengajarkan kita bahwa manifold yang bertingkat dalam lingkaran sama sekali tidak sederhana, dan lebih licik daripada yang kita harapkan."

Pada saat yang sama, teorema bundel virtual berarti bahwa ada resep sederhana dan informatif untuk membuat semua manifold 3-hiperbola yang kompak: mulai dengan permukaan yang menebal, rekatkan perbatasan bagian dalam dan luarnya dengan rotasi sesuai selera Anda, dan lipat lipatan itu ke dirinya sendiri beberapa kali.

"Jika Anda meminta saya untuk berjenis 3 hiperbolik, saya akan bertanya jenis apa yang Anda butuhkan - jenis bundel dan penutup akhir apa? - kata Kalegari. "Sekarang kita tahu bahwa dalam proses ini kita tidak melewatkan satu manifold-tunggal."

Meskipun ahli matematika akan membutuhkan waktu untuk menguji pekerjaan Eigol secara menyeluruh, banyak dari mereka yang optimis akan lulus ujian.

"Jan Aigol bukan orang yang ceroboh," kata Minsky.

Sekarang, rupanya, pertanyaan terakhir dari daftar Thurston telah diselesaikan, para peneliti mulai bertanya-tanya seperti apa wilayah topologi manifold 3 akan terlihat seperti di dunia baru yang berani setelah Thurston.

Matematikawan setuju bahwa mereka akan memiliki banyak pekerjaan untuk menemukan hal-hal berguna yang dapat ditawarkan QC untuk formulir yang dapat dibuat-potong. Dan untuk 3 manifold itu sendiri, menurut Aigol, akhir zaman telah tiba - dan awal berikutnya.

"Di sebagian besar bidang matematika tidak ada rencana yang dapat menguraikan jalur untuk 20-30 tahun ke depan, seperti halnya dengan kita," katanya. Sekarang, ia menyarankan, topologi 3-manifold dan geometri dapat menjadi serupa dengan bidang matematika lainnya di mana para ilmuwan menyentuh dan membuat kemajuan bahkan tanpa kemewahan dari gambaran hipotetis besar tentang apa yang terjadi.

"Generasi baru ahli matematika akan datang dengan pertanyaan-pertanyaan penting berikut," kata Aigol.

Kami mendapatkan bentuk: dari geometri hiperbolik ke kompleks kubik dan sebaliknya