Tentang apa artikel ini
( ) , : , , . . , . , , : , , , . , . , . ?
Dan tepat sebelum memulai, saya ingin segera memperingatkan Anda - saya bukan seorang fisikawan, karena itu model yang dibangun akan lebih seperti sketsa, contoh di mana prinsip dasar yang diterapkan di sini dapat mengarah. Artikel ini tidak berpura-pura sebagai segala jenis ilmiah, semi-ilmiah, kebenaran atau kebenaran, tidak akan ada bukti, formula, dan pertimbangan yang lengkap dari seluruh pohon keputusan. Artikel ini lebih mungkin merupakan hasil dari membangun dan menerapkan algoritma serakah untuk menyelesaikan masalah, dan seperti yang Anda tahu, algoritma serakah tidak selalu memberikan jawaban yang benar. Jadi saya memperingatkan Anda.Algoritma
Jadi, tugas kita adalah membangun model Alam Semesta, dipersenjatai dengan prinsip dasar. Untuk ini, pertama, kami akan mendukung dua invarian:-, , , . , — . — .
Saat ini, dari seluruh ragam pengetahuan tentang Alam Semesta, kita hanya akan tertarik pada mereka yang paling banyak melanggar Invarian 1. Ada Alam Semesta yang kita amati, yang terdiri dari ruang, energi, materi (dan mitra gelapnya), gravitasi, dan waktu. Karena waktu pada dasarnya adalah jarak, ia dapat dengan aman dikeluarkan dari pertimbangan dan perlu diingat bahwa segala sesuatu yang berlaku untuk jarak juga dapat diterapkan pada waktu.
, . , . — , , , , , , . .
1.
— , , , . , 1.
? ( ), . . , , , .
2.
, 2 (, ), - , , . , — ( ) 2. , , — . 2 - . .
3.
— - . , , 2 , , ? , . , , ? ? . — . , — , , .
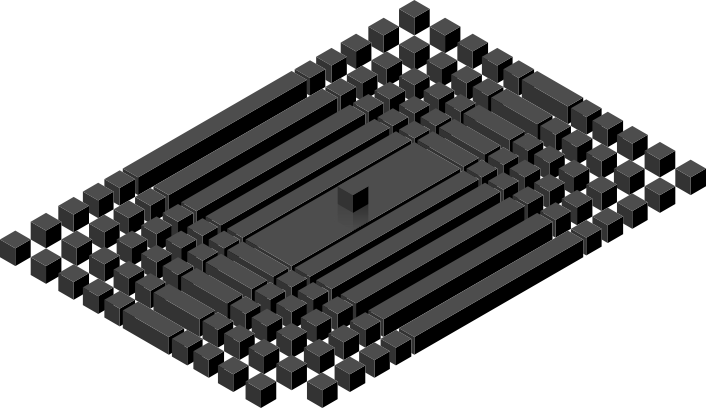Kami mengganti partikel dasar dan ruang dengan kuantum ruang (selanjutnya, kata kuantum berarti kuantum ruang, dalam kerangka artikel ini adalah istilah independen yang tidak ada hubungannya dengan kuantum tradisional dalam fisika). Tidak terlalu jelas apa ini memberi kita, tetapi kita memiliki invarian yang dipulihkan 1. Kami akan mengembalikan invarian 2 dalam semua langkah selanjutnya tanpa melanggar invarian 1.Langkah 4. Properti Quantum
.
. , 2. . — ( ).
, — , — ? , ? . , .
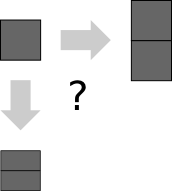
Akan lebih baik untuk menjawab pertanyaan - bagaimana tepatnya kuantum menghasilkan salinannya? Ternyata kuantum itu sendiri adalah objek yang kompleks. Mungkin dia mengkloning dirinya sendiri, mungkin dia diregangkan, tetap satu dan seluruh Semesta terdiri dari satu string panjang, dipelintir menjadi bola. Padahal, artikel ini tidak begitu penting. Untuk saat ini, kami menganggap bahwa perangkat kuantum yang tidak terlalu rumit tidak akan melanggar invarian 1.. , , , . , , , .
, .
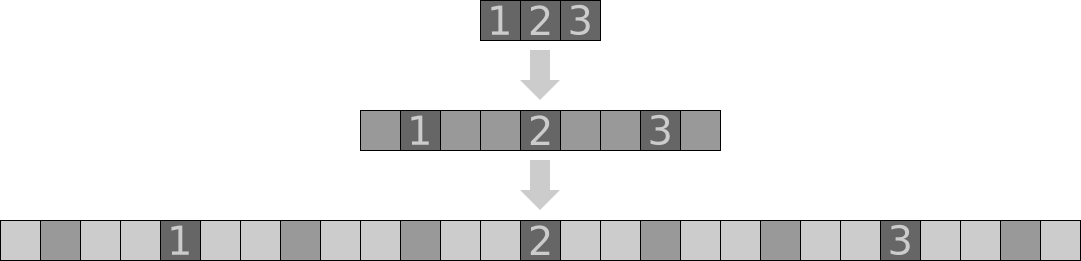
5.
- , . ? — , , , .
. , . — . , . , .
3. , . — , .
, . ? . , , ?
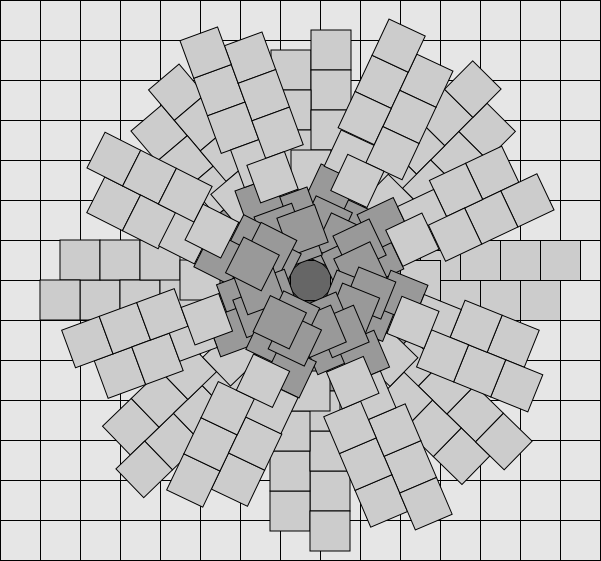Sekitar kuantum seperti itu akan selalu ada daerah dengan peningkatan kepadatan ruang, yang akan jatuh berbanding terbalik dengan jarak dari pusat (untuk pengamat eksternal) sampai sama dengan kepadatan rata-rata ruang sekitarnya. Ini sudah menjadi kandidat yang baik untuk peran partikel dasar, tetapi saya tidak ingin memperkenalkan sifat tersembunyi tambahan untuk kuanta, dan berbagai kuanta berbeda - kuanta harus semua sama.Dan bisakah partikel dasar seperti itu bergerak di ruang angkasa? Dalam arti tertentu, ya, tetapi hanya terus bergerak menjauh dari segala sesuatu di sekitarnya.— , . — , . . , , ? , , .
, , . , , , . — , .
, , . , . .
, . , 1 , — .
6.
— . . , . , , . . ( ) — . , , . ? — . , . , . , . , , , . ? — , . , , , . - , . , — , , . .
Langkah 7. Massa
Kami memiliki alam semesta yang mengembang dan memiliki partikel stabil pertama. Pada langkah ini, saya mengusulkan untuk naik ke level yang lebih tinggi dan menganggap partikel stabil sebagai satu objek. Partikel stabil memiliki dua sifat yang berguna - tidak mungkin mendekati intinya dan partikel ini menyerap ruang. Bonus dari perilaku ini adalah penampilan massa untuk partikel seperti itu, dan semakin besar massa, semakin besar tingkat penyerapan ruang oleh partikel ini.
Jika dua partikel dibiarkan menggantung tanpa bergerak di ruang, mereka akan menyerap ruang di sekitar mereka sampai sama sekali tidak ada ruang di antara mereka. Kemudian keduanya akan saling bertabrakan, mereka akan terus mendekat sedikit, kemudian bergerak menjauh, terus-menerus terbang melewati inti tetangga. Dari sudut pandang partikel - mereka bergerak ke arah satu sama lain, terbang, bergerak sedikit dan mendekat lagi. Jadi, pada langkah ini, kami memulihkan gravitasi dan kemungkinan besar menyingkirkan materi gelap. Gravitasi dalam model kami tidak lebih dari penyerapan ruang oleh materi. Terlebih lagi, jika dua partikel saling bergantungan cukup jauh, maka, mulai dari jarak tertentu, kecepatan penyerapan dua partikel tidak akan cukup untuk mengatasi perluasan Semesta, dan partikel semacam itu akan mulai bergerak menjauh satu sama lain.Langkah 8. Kesimpulan
Pada langkah ini, pada prinsipnya, dimungkinkan untuk menyelesaikan operasi algoritma, karena 2 invarian dikembalikan. Pada tingkat materi, hukum kekekalan energi harus sudah bekerja, yang umumnya tidak selalu bekerja pada tingkat kuanta., . , , , . , . . , , , , . . . , , . , .
Sama seperti suara yang merambat di air, gelombang gravitasi dari tumbukan benda besar merambat dalam bentuk kerapatan yang berubah.Bahkan jika partikel tidak memiliki massa, ia masih akan tertarik ke objek dengan massa, dan terbang di sebelahnya akan mengubah jalurnya. Sebuah partikel stasioner di orbit, misalnya, Bulan pada akhirnya akan jatuh ke permukaannya bersamaan dengan kuanta ruang yang mengelilingi objek ini. Sampai permukaan bulan menyentuh partikel seperti itu, ia akan mengalami gravitasi nol.Kita, di Bumi, berada di dalam air terjun raksasa, tetapi alih-alih air, aliran ruang jatuh ke atas kita.Dalam model kami, semua ini dimungkinkan karena asimetri kuantum dan nilai tepat probabilitas (atau frekuensi) pembuatan kuantum dan penyerapan baru. Nilai yang tepat melanggar invarian 1, oleh karena itu dapat diasumsikan bahwa dalam Tidak ada ada banyak kuanta yang berbeda, dengan asimetri yang berbeda dan nilai probabilitas yang berbeda. Dari jumlah tersebut, kita berakhir dengan hal-hal aneh yang berbeda, kadang-kadang alam semesta.Cara memeriksa
Mungkin cara termudah untuk memeriksa apakah ruang dikuantisasi dan apakah ruang diserap oleh materi adalah dengan mensimulasikan rotasi bintang di galaksi relatif terhadap intinya. Jika dimungkinkan untuk menghilangkan perbedaan antara teori dan pengamatan dalam kecepatan rotasi antara bintang-bintang yang lebih dekat ke inti dan bintang-bintang di pinggiran, maka ruang kemungkinan besar dikuantisasi.Pilihan lain adalah mencoba membuat model proton dan elektron dan melihat bagaimana mereka akan berperilaku.