Geekly articles weekly

Cara adil memotong kue

Ilmuwan komputer telah mengembangkan algoritma pie yang adil untuk sejumlah orang




Dua ilmuwan muda, para ahli di bidang ilmu komputer, menemukan cara berbagi kue secara jujur ​​di antara sejumlah orang, memecahkan masalah yang telah diperjuangkan para ahli matematika selama beberapa dekade. Pekerjaan mereka mengejutkan banyak peneliti yang menganggap pemisahan seperti itu mustahil secara prinsip.

Berbagi pai adalah metafora untuk berbagai tugas kehidupan nyata, termasuk membagi objek kontinu tertentu, apakah itu kue atau sebidang tanah, antara orang yang menghargai propertinya secara berbeda. Yang satu suka lapisan cokelat, yang lain menginginkan bunga krim. Sejak zaman Alkitab, sebuah algoritma telah dikenal untuk membagi objek semacam itu di antara dua orang, sehingga tidak ada yang akan iri pada yang lain: satu orang membagi kue menjadi dua bagian yang sama baginya, dan yang lain memilih salah satu dari mereka. Dalam Kejadian, Abraham (kemudian dikenal sebagai Abram) dan Lot menggunakan metode ini untuk membagi tanah, ketika Abraham menemukan pemisahan, dan Lot memilih antara Yordania dan Kanaan.

Pada 1960-an, matematikawan datang dengan algoritma untuk kue split seperti "tanpa iri" untuk tiga orang. Namun hingga saat ini, solusi terbaik dari masalah bagi banyak orang adalah lebih dari tiga prosedur, didirikan pada tahun 1995 ilmuwan politik Stephen Brahms [Steven Brams] dari New York University dan ahli matematika Alan Taylor [Alan Taylor] dari Union College. Itu menjamin pembagian kue yang "adil", tetapi dengan satu syarat - prosedurnya "tidak terbatas", yaitu, jumlah langkah yang diperlukan untuk berbagi akan menjadi besar secara sewenang-wenang.

Algoritma Brahms-Taylor pernah disebut sebagai terobosan, tetapi "itu tidak terbatas, menurut saya, adalah kelemahan besar," kata Ariel Procaccia[Ariel Procaccia], seorang ilmuwan komputer di Universitas Carnegie Mellon, salah satu pencipta Spliddit , alat online gratis untuk pembagian tugas yang adil, dari tugas rumah tangga hingga biaya sewa bersama.

Selama 50 tahun terakhir, banyak ahli matematika dan ilmuwan komputer, termasuk Procaccia, telah meyakinkan diri mereka sendiri bahwa tidak ada algoritma yang adil terbatas untuk membagi kue menjadi n bagian.

“Tugas inilah yang membawa saya ke bidang pembagian yang adil,” kata Walter Stromkvist[Walter Stromquist], profesor matematika di Brin Mavre College di Pennsylvania, yang mencapai hasil yang baik dalam masalah berbagi kue pada tahun 1980. "Sepanjang hidup saya, saya berpikir bahwa saya akan kembali ke tugas ini di waktu luang saya dan membuktikan bahwa perpanjangan hasil seperti itu mustahil pada prinsipnya" .

Tetapi, pada bulan April, dua spesialis dalam ilmu komputer membantah harapan ini dengan menerbitkan algoritma untuk pembagian kue secara adil dengan waktu operasi tergantung pada jumlah peserta dalam berbagi, dan bukan pada preferensi pribadi mereka. Seorang ilmuwan, Simon Mackenzie , Ph.D dari Carnegie Mellon , 27 tahun , mempresentasikan karyanya pada 10 Oktober di dasar-dasar ilmu komputer IEEE tahunan ke-57.

Algoritma ini sangat kompleks. Partisi kue antara n peserta mungkin memerlukan hingga nn n n n n langkah, dengan kira-kira jumlah pemotongan yang sama. Bahkan untuk sejumlah kecil partisipan, jumlah ini melebihi jumlah atom di alam semesta. Tetapi para peneliti sudah memiliki ide-ide untuk menyederhanakan dan mempercepat algoritma, menurut anggota tim kedua, Haris Aziz , seorang spesialis ilmu komputer berusia 35 tahun di Universitas New South Wales, yang bekerja di kelompok penelitian data Australia Data61.

Para ahli yang mempelajari teori pembagian yang adil , menurut Procaccia, menganggap ini "pasti hasil terbaik selama beberapa dekade."

Potongan kue


Algoritma Aziz dan Mackenzie didasarkan pada prosedur elegan yang ditemukan secara independen oleh ahli matematika John Selfridge dan John Conway pada 1960-an, yang memungkinkan Anda membagi kue menjadi tiga.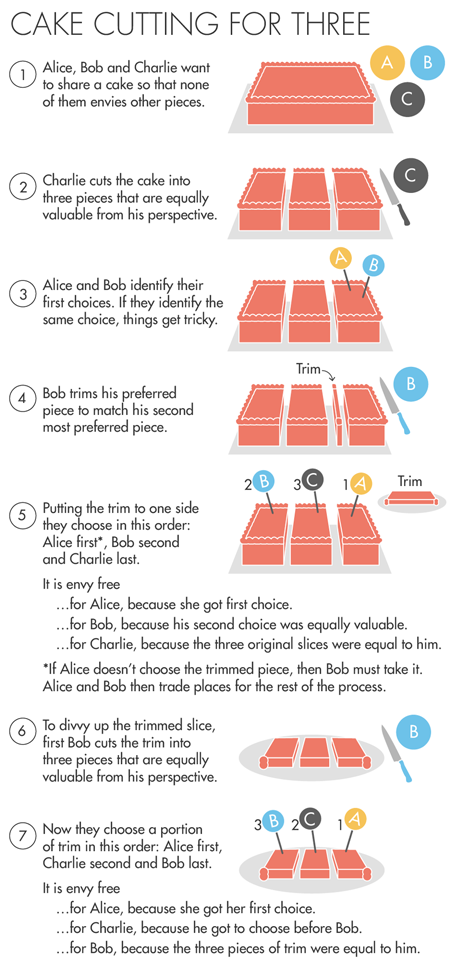



Jika Alice, Bob, dan Charlie (A, B, C) ingin membagi kue, algoritma dimulai dengan Charlie membagi kue menjadi tiga potong yang terlihat sama baginya. Alice dan Bob memilih bagian yang mereka sukai. Jika mereka memilih bagian yang berbeda - voila, semua orang mendapatkan apa yang mereka inginkan.

Jika Alice dan Bob memilih satu potong, maka Bob memotong sebagian kecil dari potongan ini sehingga potongan itu menjadi setara, dalam pandangannya, dengan sepotong kue lainnya - salah satu yang akan dipilih Bob di tempat kedua. Residu cut off ditunda. Sekarang Alice harus memilih potongan terbaik untuk dirinya sendiri dari tiga yang tersisa, dan kemudian memilih Bob - dengan syarat bahwa ia akan mengambil potongan itu, jika Alice tidak memilihnya. Charlie mendapat bagian ketiga.

Akibatnya, tidak ada yang iri pada siapa pun. Alice memilih yang pertama. Bob menerima salah satu dari dua bagian yang bernilai sama dengannya. Charlie mendapatkan salah satu dari tiga potongan asli yang dia potong sendiri.

Hanya sedikit cut-off yang tersisa. Tapi itu dapat dibagi tanpa memulai algoritme terlebih dahulu dan tanpa jatuh ke dalam siklus sunat dan pilihan tanpa akhir, karena Charlie dalam hal apapun puas dengan karyanya - dan bahkan jika orang yang mendapat potongan akan menerima seluruh sisa dalam lampiran itu, untuk Charlie tidak akan terlihat tidak jujur, karena potongan yang dipotong dan sisanya akan memberikan sepotong kue yang setara dengan potongannya - setelah semua, ia memotong potongan-potongan ini dari awal. Aziz dan Mackenzie menggambarkan posisi Charlie sebagai "dominan."

Sekarang, jika, misalnya, Alice mendapat potongan, maka Bob memotong garis menjadi tiga bagian, setara dari sudut pandangnya, Alice memilih salah satu dari potongan-potongan ini untuk dirinya sendiri, lalu memilih Charlie, lalu Bob. Semua orang senang: Alice memilih yang pertama, Charlie mendapat bagian yang lebih baik daripada Bob (dan dia tidak peduli berapa banyak yang Alice ambil), dan dari sudut pandang Bob, ketiga bagian itu setara.

Brahms dan Taylor menggunakan properti "dominasi" (tetapi dengan nama yang berbeda) untuk mengembangkan algoritma 1995 mereka, tetapi mereka tidak menyelesaikan ide mereka sampai algoritma terbatas muncul. Dalam 20 tahun ke depan tidak ada yang mencapai hasil terbaik. "Dan bukan karena kurangnya upaya," kata Procaccia.

Pembagi Kue Tidak Profesional


Ketika Aziz dan Mackenzie (A&M) memutuskan untuk mengambil tugas ini beberapa tahun yang lalu, mereka baru dalam tugas berbagi kue. "Kami tidak memiliki pengalaman sebanyak orang yang bekerja secara intensif di atasnya," kata Aziz. "Meskipun ini biasanya kekurangan, dalam kasus kami itu merupakan keuntungan, karena kami berpikir secara berbeda."

A&M dimulai dengan mempelajari tugas membagi menjadi tiga peserta dari awal, dan sebagai hasil analisis datang ke algoritma adil terbatas untuk empat peserta , yang diterbitkan oleh mereka tahun lalu.

Mereka tidak dapat langsung menunjukkan bagaimana memperluas algoritma mereka ke sejumlah peserta yang lebih besar dari empat, tetapi mereka dengan antusias mengambil tugas ini. "Setelah mengirim karya mengenai empat peserta, kami benar-benar ingin segera melanjutkan pekerjaan sampai seseorang lebih berpengalaman dan pintar menyamaratakannya secara mandiri untuk kasus n peserta," kata Aziz. Dan setelah sekitar satu tahun, pencarian mereka berhasil.

Seperti algoritma Selfridge-Conway, protokol AiM terus-menerus menawarkan peserta yang berbeda untuk memotong kue menjadi n bagian yang sama, dan yang lain untuk memotong dan memilih potongan kue. Tetapi ada langkah-langkah lain dalam algoritma, misalnya, pertukaran potongan kue secara berkala dengan cara khusus, untuk meningkatkan jumlah hubungan dominan antara para peserta.

Hubungan ini memungkinkan A&M untuk mengurangi kompleksitas tugas. Jika, misalnya, tiga peserta mendominasi sisanya, mereka sudah dapat dikirim untuk memakan kue mereka sendiri - mereka akan bahagia terlepas dari siapa yang mendapat sisanya. Setelah ini, lebih sedikit peserta tetap, dan setelah sejumlah langkah tersebut, semua orang puas dan seluruh kue dibagi.

"Melihat kembali kompleksitas algoritma, tidak mengherankan bahwa butuh waktu lama untuk mengembangkannya," kata Procaccia. Tapi Haim sudah percaya bahwa mereka dapat menyederhanakan algoritma, sehingga tidak memerlukan pertukaran potongan dan lulus hanya n n n langkah. Menurut Aziz, mereka sudah mengerjakan hasil ini.

Brahms memperingatkan bahwa bahkan algoritma yang lebih sederhana tidak akan memiliki aplikasi praktis - setelah semua, potongan kue yang diterima oleh para peserta akan mencakup banyak remah-remah kecil dari berbagai bagian kue. Pendekatan ini tidak terlalu berguna jika, misalnya, Anda membagi tanah.

Tetapi bagi para ilmuwan matematika dan komputer yang mempelajari masalah tersebut, hasil baru "mengatur ulang seluruh topik," kata Stromkvist.

Sekarang para peneliti tahu bahwa kue dapat dibagi dalam sejumlah langkah terbatas, langkah selanjutnya, menurut Procaccia, adalah untuk memahami kesenjangan besar antara batas atas pada jumlah langkah dengan metode AiM dan batas bawah pada jumlah langkah yang diperlukan untuk ini. Procaccia telah membuktikan sebelumnya bahwa algoritma untuk pemisahan kue yang adil tidak dapat lewat kurang dari n2 langkah - tetapi jumlah langkahnya kecil dibandingkan dengan n n n n n n dan bahkan n n n .

Aziz mengatakan para peneliti sekarang harus mencari cara untuk mempersempit kesenjangan ini. "Saya pikir kemajuan dapat dibuat di kedua arah."

Source: https://habr.com/ru/post/id398683/

More articles:


All Articles