Penomoran jalan dan matematika AS
Neil: Bagaimana saya bisa menyusuri jalan yang tidak ada ke kota yang mungkin juga tidak ada?
O. Grant: Ya, ada nomor yang tidak ditentukan. Mengapa tidak jalan raya dan kota?
- Tidak, tidak akan. Pasti ada penjelasan yang lebih baik dari itu.
- Penjelasan terbaik? Oke, mungkin pengukuran paralel atau mimpi, atau mungkin itu terkait dengan keinginan Anda, atau apakah Anda koma setelah mengenai ember itu, dan mungkin ... mungkin Anda mati?
Film "Rute 60: Kasus di Jalan", 2002Matematika dapat dilihat dalam banyak cara yang mengelilingi kita setiap hari. Ada pendapat bahwa prinsip-prinsip matematika terkait erat dengan apa yang kita amati di Alam Semesta di sekitar kita. Rasio emas, fraktal, kisi kristal, serangkaian angka Fibonacci. Dan ada sistem penomoran jalan raya di AS. Anda semua telah melihat dalam kenyataan atau di bioskop, bagaimana orang Amerika menentukan jalan dengan angka dan huruf.3. Dan sistem ini diciptakan pada tahun ini dan itu. Dan mereka melakukannya bukan tanpa bantuan matematika dasar. Tujuannya adalah untuk melakukan ini (untuk memudahkan orang kebanyakan, seperti yang saya mengerti).Artikel ini akan membahas tentang jalan raya di Amerika. Tampaknya hal khusus seperti itu diperlukan untuk memetakan jalan negara - menata angka-angka, itulah keseluruhan kerumitannya. Tapi tidak, di setiap nama jalanbeberapa makna tersembunyi : arah, pentingnya jalan dan sesuatu yang lain. Sistem ini ditemukan dengan bantuan matematika dasar sehingga lebih mudah bagi pengemudi untuk menggunakan kanvas panjang jalan Amerika.Beberapa fakta menarik
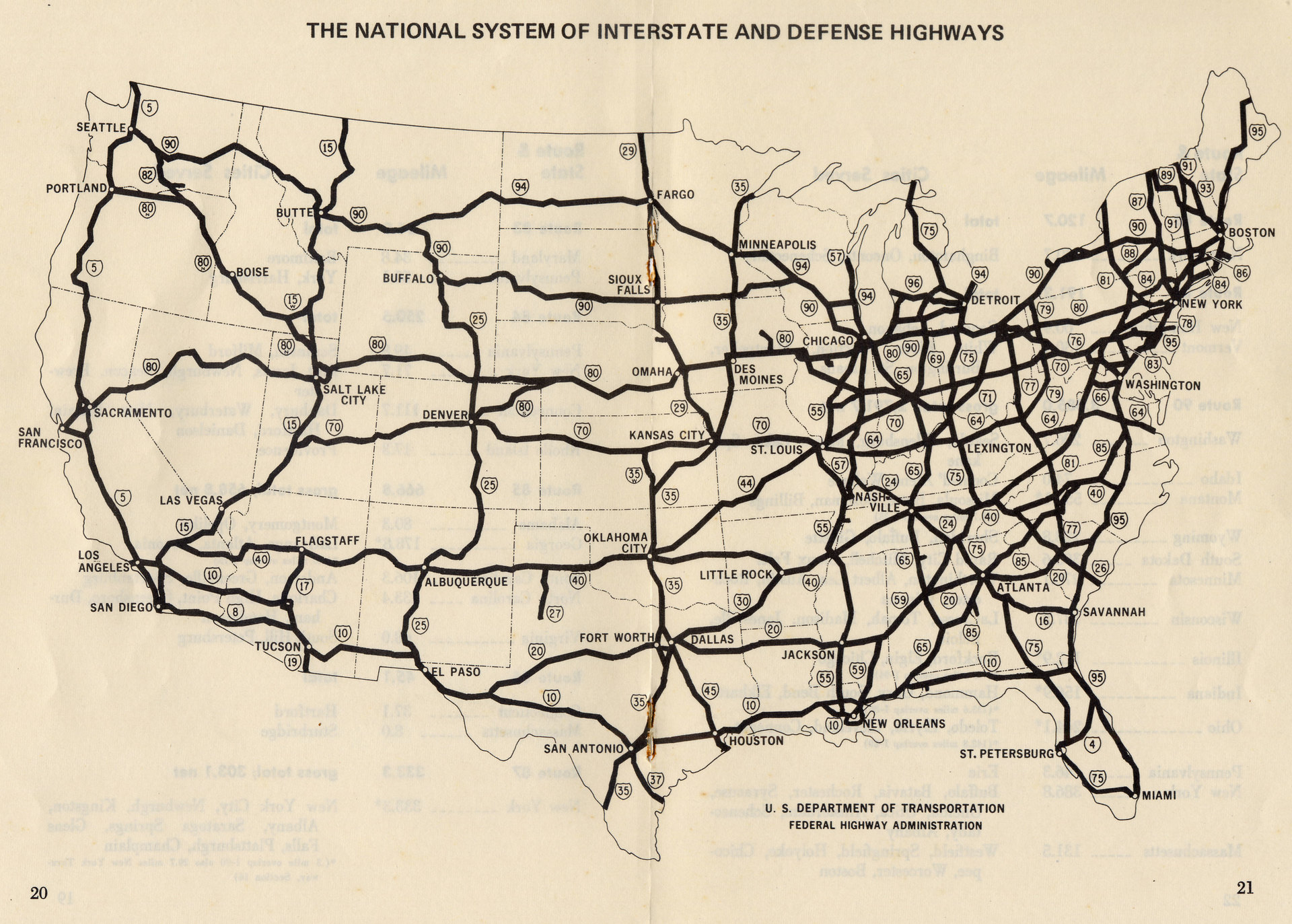
- Skema Penomoran Jalan Raya Interstate dikembangkan oleh American Association of State Highways and Transportation pada tahun 1957. Kebijakan pelabelan saat ini telah dipertahankan sejak 1973.
- Di dalam perbatasan benua Amerika Utara, jalan raya utama ditandai dengan angka kurang dari 100.
- Tidak ada jalan raya dengan angka I-60 dan I-50 di AS. Mereka seharusnya melalui negara bagian dengan jalan AS dan nomor yang sama, tetapi angka yang berulang dilarang oleh hukum.
- . . , - I-35E I-35W. I-35, .
Bagi seorang pelancong yang tidak siap , peta jalan AS mungkin tampak membingungkan, seperti jaringan kereta bawah tanah kota-kota seperti New York atau London. Tetapi jika peta disajikan dalam bentuk yang diluruskan, maka kita akan melihat kotak geometris.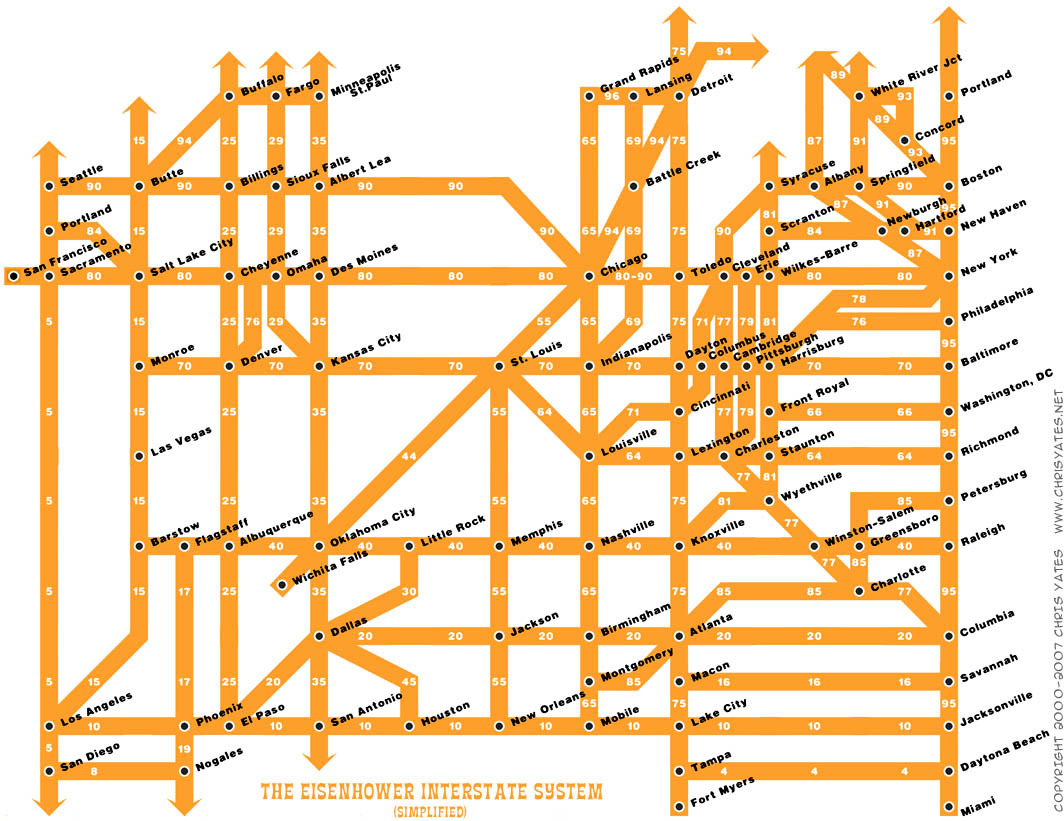
Menurut sistem penomoran yang diadopsi, jalan dengan angka genap memiliki arah timur-barat. Misalnya, I-10, I-90. Huruf "I" di depan angka menunjukkan "Interstate" (Interstate). Jalan dengan tanda-tanda aneh membentang dari utara ke selatan. Misalnya, I-5, I-95. Penomorannya meningkat dari barat daya ke arah timur laut - dari sudut kiri bawah peta ke kanan atas. Sebutan aneh adalah dari barat ke timur, dan yang genap dari selatan ke utara.Disebutkan I-5 terletak di Pantai Barat, dan I-95 - di Timur. Ternyata I-10 terjadi di Texas, dan I-90 di Massachusetts. Jalan utama ditunjukkan oleh angka yang merupakan kelipatan lima - mereka meningkat dari utara ke selatan, mulai dari I-5 dan berakhir dengan I-95.Jalan raya antar negara bagian dipasangkan dengan tiga angka. Misalnya, 290 berpotongan dengan yang ke-90, 495 dengan yang ke-95. Mereka bisa melingkar, radial atau bercabang. Angka tiga digit dibentuk dengan menambahkan satu digit ke angka dua digit dari jalan antar negara terdekat: cabang menerima angka ganjil (190), dan yang radial dan cincin menerima angka genap (495). Karena sistem ditemukan oleh manusia, Anda dapat menemukan pengecualian untuk pola yang dijelaskan.Dalam rangkaian digital sederhana ini, banyak informasi dienkripsi. Tanpa kartu di tangan, Anda dapat menentukan dengan nomor jalan di mana Anda saat ini dan di mana Anda akan mendapatkan.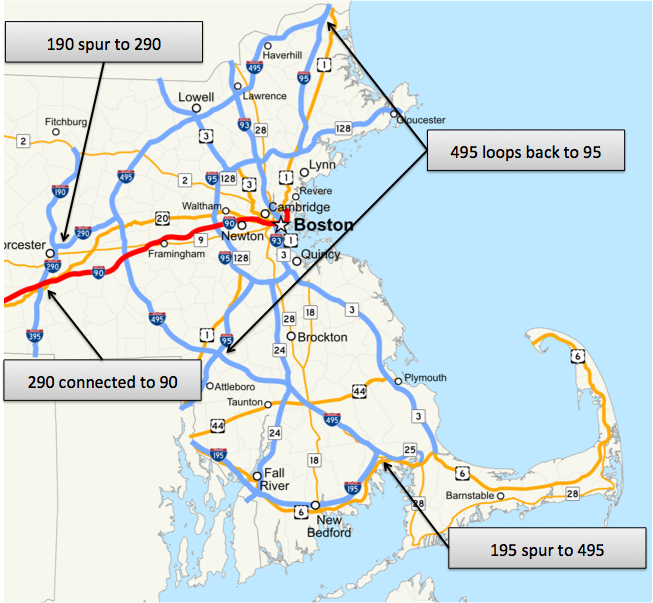
Contoh
Ambil jalan dengan nomor acak 321. Ini adalah jalan ke mana salah satu jalan utama dan jalan antar negara dengan nomor 21 bergabung. Dan jalan dengan nomor 21 akan berjalan lebih banyak di pantai barat daripada di timur.Dipandu hanya oleh seperangkat prinsip di atas, kita dapat mengatakan bahwa dari Seattle ke Boston dapat dicapai oleh I-90. Dan jika Anda menyimpang dari jalur langsung, maka, misalnya, di selatan I-95 Anda dapat menelepon di Florida, dan kemudian saya-10 barat ke Los Angeles, dan akhirnya kembali ke Seattle di I-5 utara.Bagaimana cara kerjanya?
Ada konsep angka dengan semua karakteristiknya seperti paritas, besarnya, jumlah digit, dan sebagainya. Juga, orang memperhatikan bahwa objek dari dunia nyata, seperti jalan raya, juga memiliki sifat yang berbeda: arah, lokasi, tingkat kepentingan hierarkis.Jadi penulis sistem penomoran jalan menghubungkan properti nomor ke properti objek jalan.| Properti nomor | Pengaturan jalan bebas hambatan |
| genap / ganjil | arah S \ S dan B \ W |
| urutan numerik | memesan Z-V dan Yu-S |
| dua digit | Jalan Bebas Hambatan Antar Negara |
| tiga digit | jalan antar negara bagian kurang signifikan |
Inilah esensi pemikiran matematika. Ini bukan tentang operasi aritmatika cepat atau rumus menghafal, tetapi tentang cara menghubungkan pola. Matematika adalah kumpulan benda-benda abstrak yang kita korelasikan dengan benda-benda dari kehidupan nyata. Kegunaan benda-benda abstrak sepenuhnya bergantung pada imajinasi manusia.Apa lagi
Sekarang tentang bilangan prima.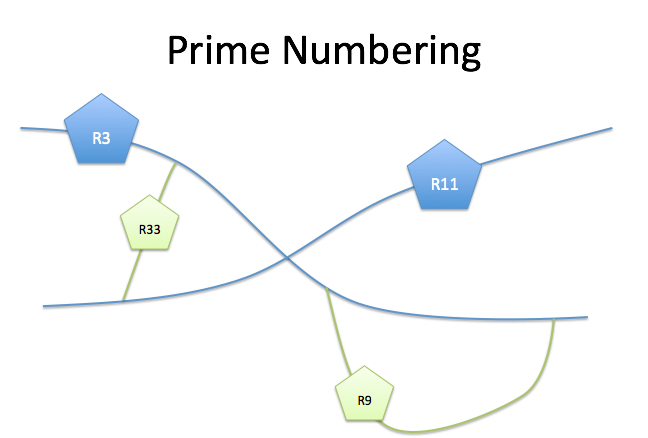
Diasumsikan bahwa bilangan prima kecil digunakan untuk arah lokal: 2, 3, 5, 7, 11. Ketika semua rute utama diberi nomor, jalan yang lebih kecil yang menghubungkan rute utama dapat mengikuti aturan berikut: ketika menggabungkan dua arah dalam nama, gunakan pekerjaan mereka.Contoh
Jalan 5 menghubungkan dengan jalan 11, kita mendapatkan arah 55.Dan jika Anda tersesat pada rute dengan satu angka, persegi itu, 5 * 5 = 25. Ini berarti bahwa rute 25 menghubungkan rute 5 dengan dirinya sendiri. Jika Anda menghubungkan tiga jalan, itu bisa berupa rute, misalnya, 66 - 2 * 3 * 11. Dua penomoran jalan primer saat dikalikan akan memberikan angka unik. 33 tidak akan pernah berfungsi sebagai produk dari dua pasang jalan raya utama yang berbeda. Setiap angka memiliki faktorisasi utama yang unik.Source: https://habr.com/ru/post/id399235/
All Articles