Struktur misterius menggabungkan matematika dan alam

Di kota Cuernavaca di Meksiko, jaringan "mata-mata" meningkatkan efisiensi armada bus. Akibatnya, jadwal keberangkatan bus selalu sesuai dengan pola "universalitas"

Pada tahun 1999, ketika duduk di halte bus di Cuernavaca, Meksiko, fisikawan Ceko Petr Šeba memperhatikan orang-orang memberi supir bis kertas untuk ditukar dengan uang. Dia menemukan bahwa ini bukan manifestasi dari kejahatan terorganisir, tetapi perdagangan "bayangan" yang berbeda: masing-masing pengemudi membayar "mata-mata," mencatat ketika bus sebelumnya berangkat dari halte. Jika dia pergi baru-baru ini, pengemudi bus ini melambat sehingga penumpang bisa berkumpul di halte berikutnya. Jika bus itu berangkat sejak lama, pengemudi mempercepat sehingga bus lain tidak akan menyusulnya. Sistem seperti itu memaksimalkan keuntungan pengemudi. Yang memberi Sheba ide.

"Kami pikir kami mengamati situasi yang sedikit mengingatkan pada sistem kuantum yang kacau," jelas rekan penulis Sheba, Milan Krbálek.

Setelah beberapa upaya yang gagal untuk berkomunikasi dengan "mata-mata," Sheba meminta muridnya untuk menjelaskan bahwa dia bukan dari pajak atau dari mafia. Dia hanyalah seorang ilmuwan gila yang mengubah tequila menjadi data mereka. Dan orang-orang memberinya catatan mereka. Ketika para peneliti merencanakan ribuan waktu keberangkatan bus, kecurigaan mereka dikonfirmasi. Interaksi antara pengemudi menyebabkan distribusi kesenjangan antara limbah transportasi, yang bertepatan dengan struktur beberapa eksperimen dalam fisika kuantum.

"Saya berpikir bahwa sesuatu seperti ini mungkin muncul, tetapi saya terkejut melihat kebetulan yang persis seperti itu," kata Sheba.

Partikel-partikel subatomik memiliki sedikit kesamaan dengan sistem bus terdesentralisasi. Tetapi selama bertahun-tahun sejak penemuan interaksi kuantum yang aneh, struktur data yang sama telah muncul dalam situasi lain yang tidak terkait. Para ilmuwan percaya bahwa fenomena umum ini, yang dikenal sebagai "universalitas", disebabkan oleh koneksi matematis dari fenomena, dan membantu mereka untuk mensimulasikan sistem yang kompleks, dari Internet hingga iklim planet ini.


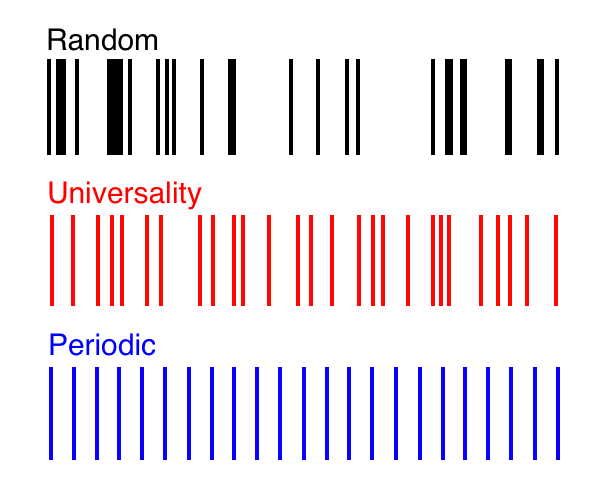Grafik merah mewakili keseimbangan sempurna antara keacakan dan periodisitas, yang dikenal sebagai universalitas. Itu diamati dalam spektrum banyak sistem kompleks dengan korelasi. Dalam spektrum ini, fungsi korelasi matematis memberikan probabilitas tepat dari keberadaan dua garis pada jarak yang diberikan satu sama

lain.Struktur semacam itu pertama kali ditemukan di alam pada tahun 1950 dispektrum energi inti uranium , monster dengan ratusan bagian yang bergerak, berosilasi dan meregangkan dalam jumlah cara yang tak terbatas, dan memberikan urutan tingkat energi yang tak terbatas. Pada tahun 1972, Hugh Montgomery, seorang spesialis dalam teori bilangan, mengamatinya di nol fungsi Riemann zeta , sebuah objek matematika yang berkaitan dengan distribusi bilangan prima. Pada tahun 2000, Krbalek dan Sheba menemukannya di jadwal keberangkatan bus di Cuernavaca . Dan baru-baru ini, ia muncul dalam pengukuran spektral bahan komposit, seperti es laut dan jaringan tulang manusia, dan dalam dinamika sinyal dari model ErdLF-Reni , versi Internet yang disederhanakan.

Setiap sistem ini memiliki spektrum - urutan barcode yang mewakili data seperti tingkat energi, nol nol, waktu keberangkatan bus, atau kecepatan sinyal. Struktur identik muncul di seluruh spektrum. Distribusi data terlihat acak, tetapi pada saat yang sama, garis-garis yang berdekatan “saling tolak”, yang mengarah pada keteraturan tertentu dari kesenjangan. Keseimbangan yang tepat antara kekacauan dan ketertiban, ditentukan oleh rumus, juga muncul dalam masalah matematika murni: ia menentukan jarak antara nilai-nilai eigen dari matriks yang diisi dengan angka acak.

"Mengapa begitu banyak sistem fisik berperilaku seperti matriks acak tetap menjadi misteri," kata Horng Tzer Yao, seorang ahli matematika di Universitas Harvard. "Tapi selama tiga tahun terakhir, kami telah mengambil langkah yang sangat penting untuk memahami hal ini."

Untuk mempelajari fenomena universalitas dalam matriks acak, para ilmuwan memiliki sedikit pemahaman tentang mengapa hal itu muncul di mana-mana dan bagaimana hal itu dapat digunakan. Dalam tumpukan makalah baru, Yao dan matematikawan lainnya menggambarkan banyak jenis matriks acak baru yang mematuhi beberapa distribusi numerik dan aturan simetri. Misalnya, angka untuk kolom dan baris matriks dapat diambil dari kurva distribusi normal dari nilai yang mungkin, atau Anda dapat mengisinya dengan nilai 1 dan -1. Bagian kanan atas dan kiri bawah dari matriks dapat saling mencerminkan, atau mungkin tidak ditampilkan. Dan terlepas dari karakteristik mereka, matriks acak menunjukkan spektrum yang kacau tapi teratur dalam distribusi nilai eigen mereka. Oleh karena itu, ahli matematika menyebut fenomena ini "universalitas."

"Itu tampak seperti hukum alam," kata Wang Wu, seorang ahli matematika di Universitas Yale, yang, bersama dengan Terence Tao dari Universitas California di Los Angeles, membuktikan universalitas untuk berbagai kelas matriks acak.

Diyakini bahwa universalitas muncul dalam sistem yang sangat kompleks, terdiri dari banyak bagian yang saling berinteraksi erat untuk menciptakan spektrum. Konfigurasi muncul dalam spektrum matriks acak, misalnya, karena semua elemen matriks digunakan dalam menghitung spektrum ini. Tetapi matriks acak, menurut Wu, hanyalah "sistem mainan", mereka cukup sederhana untuk dipelajari, dan cukup kaya untuk memodelkan sistem nyata. Fleksibilitas jauh lebih umum. Hipotesis Wigner (dinamai setelah Eugene Wigner, phyisis yang menemukan universalitas dalam spektrum atom), menunjukkan bahwa semua sistem kompleks dengan korelasi bersifat universal, dari kisi kristal ke Internet.

Semakin kompleks sistemnya, semakin universal ia memanifestasikan dirinya, kata Laszlo Erdös dari University of Munich, salah satu rekan kerja Yao. "Anda percaya universalitas adalah perilaku yang khas."

Dalam banyak sistem sederhana, komponen individu dapat terlalu banyak mempengaruhi hasil keseluruhan, yang mengubah penampilan spektrum. Sistem yang lebih besar tidak memiliki dominasi komponen tunggal. "Ternyata ada ruangan dengan banyak orang yang memutuskan untuk melakukan sesuatu, dan identitas salah satunya tidak begitu penting," kata Wu.


Matematikawan menggunakan matriks acak untuk mempelajari dan memprediksi beberapa properti Internet, misalnya, ukuran cluster komputer yang khas

Ketika suatu sistem menunjukkan universalitas, ini berfungsi sebagai jaminan bahwa itu kompleks dan ada cukup korelasi di dalamnya untuk ditafsirkan sebagai matriks acak. "Itu berarti Anda dapat menggunakan matriks acak untuk memodelkannya," kata Wu. "Anda dapat menghitung parameter model lain berdasarkan matriks dan menggunakannya untuk memprediksi perilaku sistem ini."

Teknik ini memungkinkan para ilmuwan untuk memahami struktur dan evolusi Internet. Beberapa properti dari jaringan komputer yang besar ini, seperti ukuran khas dari sekelompok komputer, dapat diperkirakan secara akurat melalui properti yang diukur dari matriks acak yang sesuai. "Orang-orang tertarik pada klaster dan lokasi mereka, dan ini sering disebabkan oleh tujuan praktis, seperti iklan," kata Wu.

Teknologi serupa dapat menghasilkan peningkatan dalam model perubahan iklim. Para ilmuwan telah menemukan bahwa keberadaan universalitas, mirip dengan spektrum energi, dalam materi menunjukkan keterkaitan yang kuat dari bagian-bagiannya, dan, sebagai konsekuensinya, konduktivitas yang baik dari cairan, listrik atau panas. Dan sebaliknya, kurangnya keserbagunaan dapat mengindikasikan jarangnya bahan dan sifat isolasi. Dalam sebuah makalah baru yang dipresentasikan pada konferensi matematika di San Diego, Ken Golden, seorang ahli matematika di Universitas Utah, dan muridnya, Ben Murphy, menggunakan perbedaan ini untuk memprediksi konduktivitas panas dan aliran fluida dalam es laut, baik pada tingkat mikroskopis dan Apsintus Arktik, hadir di wilayah yang membentang ribuan kilometer.

Pengukuran spektral dari mosaik kayu apus yang meleleh, difoto dari helikopter, atau data es laut yang diperoleh dari sampel, menunjukkan status masing-masing sistem ini. "Aliran fluida melalui es laut mendorong proses yang sangat penting yang perlu dipahami untuk memahami sistem iklim," kata Golden. "Transisi dalam statistik keputusan kami sendiri mewakili pendekatan baru yang ketat secara matematis untuk dimasukkannya es laut dalam model iklim."

Trik yang sama dapat mengarah pada tes sederhana untuk osteoporosis. Golden, Murphy dan koleganya menemukan bahwa spektrum tulang yang padat dan sehat memiliki fleksibilitas, sedangkan spektrum tulang berpori tidak.


Apsintus Arktik bersifat universal jika mereka cukup terhubung

"Kami bekerja dengan sistem yang" partikel "-nya dapat berukuran milimeter atau kilometer, kata Murphy tentang komponen sistem. "Sungguh menakjubkan bahwa matematika yang sama menggambarkan semuanya."

Alasan sistem nyata menunjukkan perilaku yang mirip dengan matriks acak mungkin paling mudah untuk dipahami dalam kasus inti atom berat. Semua sistem kuantum, termasuk atom, bekerja sesuai dengan aturan matematika, terutama dengan partisipasi matriks. "Ini adalah esensi dari mekanika kuantum," kata Freeman Dyson, mantan fisikawan matematika yang membantu mengembangkan teori matriks acak pada 1960-an dan 1970-an di Princeton Institute for Advanced Engineering. "Setiap sistem kuantum dijelaskan oleh sebuah matriks yang mewakili energi totalnya, dan solusi matriks itu sendiri adalah tingkat energi dari sistem kuantum."

Matriks atom sederhana, hidrogen dan helium, dapat dihitung secara akurat, dan solusi eigen yang diperoleh bertepatan dengan akurasi mengejutkan dengan tingkat energi atom yang diukur. Tetapi matriks dari sistem yang lebih kompleks, seperti inti uranium, menjadi terlalu "berduri" untuk "mengambilnya". Menurut Dyson, karena ini, kernel tersebut dapat dibandingkan dengan matriks acak. Banyak interaksi dalam uranium - unsur-unsur matriks yang tidak diketahui - sangat kompleks sehingga campurannya menghasilkan suara, seperti banyak suara yang dilapiskan. Akibatnya, matriks tidak dikenal yang mengontrol kernel berperilaku seperti matriks dengan angka acak, dan spektrum mereka bersifat universal.


Seperti, apsintus yang tidak terhubung, tidak memiliki universalitas, spektrumnya acak

Para ilmuwan belum mengembangkan pemahaman intuitif tentang mengapa sistem kompleks menunjukkan ini, dan bukan urutan acak / periodik lainnya. "Kami hanya tahu ini dari perhitungan," kata Wu. Misteri lain adalah hubungan mereka dengan fungsi Riemann zeta, di mana universalitas dimanifestasikan dalam spektrum nol. Nol ini terkait erat dengan distribusi bilangan prima - bilangan bulat tak tereduksi yang membentuk sisanya. Matematikawan telah lama mencari deskripsi distribusi bilangan prima pada garis bilangan dari 1 hingga tak terbatas, dan universalitas memberi mereka kuncinya. Beberapa percaya bahwa fungsi Riemann zeta mungkin cukup rumit dan koheren untuk memiliki universalitas. Penemuan matriks semacam itu akan memiliki "pengaruh kuat" pada pemahaman distribusi bilangan prima, seperti kata Paul Bourgade, seorang ahli matematika Harvard.

Mungkin saja penjelasannya disembunyikan lebih dalam. “Mungkin ternyata bahwa pusat dari universalitas dan fungsi zeta Wigner bukanlah matriks, tetapi beberapa struktur matematika yang belum ditemukan,” kata Erdös. “Matriks yang lebih ganas dan fungsi zeta dapat menjadi representasi berbeda dari struktur ini.”

Banyak ahli matematika mencari jawaban tanpa jaminan. “Tidak ada yang membayangkan bahwa bus di Cuernavac akan menjadi contoh seperti itu. Tidak ada yang membayangkan bahwa nol fungsi zeta akan menjadi contoh lain, kata Dyson. "Keindahan ilmu pengetahuan adalah hal yang tidak dapat diprediksi, dan semua yang berguna berasal dari kejutan."

Source: https://habr.com/ru/post/id399535/