 Jika kita kembali ke sejarah mempelajari jalur penerbangan dari Bumi ke Bulan, maka Anda harus kembali satu setengah abad yang lalu, pada tahun 1865, ketika novel baru Jules Verne "Dari Bumi ke Bulan dengan cara langsung dalam 97 jam 20 menit" diterbitkan. Tentu saja, ini jauh dari buku pertama yang menggambarkan penerbangan semacam itu, tetapi itu adalah novel pertama di mana penulis memutuskan untuk mendekati deskripsi perjalanan dari sudut pandang ilmiah.Selain itu, tingkat persiapan teks ini dipahami dengan baik sekarang, karena untuk pertama kalinya perjalanan ruang angkasa tidak hanya ditampilkan, tetapi semua nuansa, kadang-kadang sangat kecil, dianalisis secara rinci. Sekarang mereka suka mengkritik novel karena kesalahan yang dibuat penulis. Tetapi dengan volume kerja yang demikian, akan mengejutkan jika tidak ada kesalahan sama sekali! Dan sekarang bukan kesalahannya yang lebih membuatnya kagum, tapi apa yang benar tentangnya. Sebagai contoh, gagasan sistem pemurnian oksigen pada kulit Columbiada dan pesawat ruang angkasa Soyuz sangat mirip. Hanya Jules Verne yang memiliki natrium hidroksida, dan sekarang lithium hidroksida digunakan.
Jika kita kembali ke sejarah mempelajari jalur penerbangan dari Bumi ke Bulan, maka Anda harus kembali satu setengah abad yang lalu, pada tahun 1865, ketika novel baru Jules Verne "Dari Bumi ke Bulan dengan cara langsung dalam 97 jam 20 menit" diterbitkan. Tentu saja, ini jauh dari buku pertama yang menggambarkan penerbangan semacam itu, tetapi itu adalah novel pertama di mana penulis memutuskan untuk mendekati deskripsi perjalanan dari sudut pandang ilmiah.Selain itu, tingkat persiapan teks ini dipahami dengan baik sekarang, karena untuk pertama kalinya perjalanan ruang angkasa tidak hanya ditampilkan, tetapi semua nuansa, kadang-kadang sangat kecil, dianalisis secara rinci. Sekarang mereka suka mengkritik novel karena kesalahan yang dibuat penulis. Tetapi dengan volume kerja yang demikian, akan mengejutkan jika tidak ada kesalahan sama sekali! Dan sekarang bukan kesalahannya yang lebih membuatnya kagum, tapi apa yang benar tentangnya. Sebagai contoh, gagasan sistem pemurnian oksigen pada kulit Columbiada dan pesawat ruang angkasa Soyuz sangat mirip. Hanya Jules Verne yang memiliki natrium hidroksida, dan sekarang lithium hidroksida digunakan. Yang lebih menarik adalah saat-saat di mana dia benar, meskipun ada asumsi yang salah. Misalnya, Perelman mengkritiknya karena memberikan data yang salah tentang waktu penerbangan dari Bumi ke Bulan dan bahkan membuatnya atas nama novel. Ahli matematika melakukan perhitungan yang lebih akurat dengan metode yang ditentukan, setelah menerima angka urutan enam hari, dua hari lebih banyak daripada dalam novel. Dan perhitungannya, dalam kerangka metode ini, memang benar. Sangat mungkin untuk terbang ke Bulan hanya dalam empat hari (sebenarnya, banyak perangkat mencapai bulan sekitar waktu ini), tetapi dalam enam hari sudah tidak mungkin.Metode perhitungan yang dipilih oleh penulis fiksi ilmiah salah, dan angka itu ternyata benar!Masih, misalnya, tak lama setelah rilis novel "Around the Moon", banyak yang meragukan kemungkinan lintasan yang dekat dari terbang dekat Bulan di bawah pengaruh hanya gaya gravitasi. Hanya pada awal abad kedua puluh, ketika mengevaluasi orbit dalam sistem bintang biner, kemungkinan keberadaan orbit seperti itu benar-benar ditunjukkan. Berikut adalah apa yang ditulis oleh jurnal Bahasa Inggris "Pengetahuan" pada awal abad ke-20 dalam artikel "Astronomi oleh Jules Verne":«, . , . . , . , , . , , , . . . . , . , , , ».Dengan kata lain, tugas-tugas yang coba diselesaikan oleh Jules Verne pada waktu itu bukan hanya di garis depan sains - mereka sering mengajukan pertanyaan yang sains kemudian tidak bisa menjawab.Namun, orang tidak boleh lupa bahwa dia tidak melakukan semua ini sendirian. Saat menulis semua bukunya, penulis mencoba beralih ke spesialis di bidang apa pun. Menurut buku hariannya, perhitungan untuk penerbangan dari Bumi ke Bulan dilakukan oleh sepupunya Henri Garce (1815-1871), seorang guru matematika di Lyceum of Napoleon (sekarang Lyceum Henry IV). Ngomong-ngomong, di sini Anda dapat melihat bukunya dalam bahasa Prancis, didedikasikan untuk Kosmografi Leçons nouvelles de Cosmographie (1854). Dan perhitungannya cukup akurat. Sebagai contoh, di sini, menurut data dalam buku ini, saya menghitung tanggal mulai yang tepat untuk kru Columbiada.
Yang lebih menarik adalah saat-saat di mana dia benar, meskipun ada asumsi yang salah. Misalnya, Perelman mengkritiknya karena memberikan data yang salah tentang waktu penerbangan dari Bumi ke Bulan dan bahkan membuatnya atas nama novel. Ahli matematika melakukan perhitungan yang lebih akurat dengan metode yang ditentukan, setelah menerima angka urutan enam hari, dua hari lebih banyak daripada dalam novel. Dan perhitungannya, dalam kerangka metode ini, memang benar. Sangat mungkin untuk terbang ke Bulan hanya dalam empat hari (sebenarnya, banyak perangkat mencapai bulan sekitar waktu ini), tetapi dalam enam hari sudah tidak mungkin.Metode perhitungan yang dipilih oleh penulis fiksi ilmiah salah, dan angka itu ternyata benar!Masih, misalnya, tak lama setelah rilis novel "Around the Moon", banyak yang meragukan kemungkinan lintasan yang dekat dari terbang dekat Bulan di bawah pengaruh hanya gaya gravitasi. Hanya pada awal abad kedua puluh, ketika mengevaluasi orbit dalam sistem bintang biner, kemungkinan keberadaan orbit seperti itu benar-benar ditunjukkan. Berikut adalah apa yang ditulis oleh jurnal Bahasa Inggris "Pengetahuan" pada awal abad ke-20 dalam artikel "Astronomi oleh Jules Verne":«, . , . . , . , , . , , , . . . . , . , , , ».Dengan kata lain, tugas-tugas yang coba diselesaikan oleh Jules Verne pada waktu itu bukan hanya di garis depan sains - mereka sering mengajukan pertanyaan yang sains kemudian tidak bisa menjawab.Namun, orang tidak boleh lupa bahwa dia tidak melakukan semua ini sendirian. Saat menulis semua bukunya, penulis mencoba beralih ke spesialis di bidang apa pun. Menurut buku hariannya, perhitungan untuk penerbangan dari Bumi ke Bulan dilakukan oleh sepupunya Henri Garce (1815-1871), seorang guru matematika di Lyceum of Napoleon (sekarang Lyceum Henry IV). Ngomong-ngomong, di sini Anda dapat melihat bukunya dalam bahasa Prancis, didedikasikan untuk Kosmografi Leçons nouvelles de Cosmographie (1854). Dan perhitungannya cukup akurat. Sebagai contoh, di sini, menurut data dalam buku ini, saya menghitung tanggal mulai yang tepat untuk kru Columbiada. Henri Garcet (1815–1871)Namun, kita mungkin tidak akan tahu tentang perhitungannya jika Jules Verne tidak menempatkannya di awal buku "Around the Moon", menggunakannya dalam percakapan para kru kerang Columbiada. Mereka menulis bahwa pembaca surat kabar "Debat" tertanggal 7 November 1869 benar-benar kagum melihat perhitungan matematika yang rumit - penerbitan novel dimulai di surat kabar ini.Beginilah model matematika dari penerbangan itu dijelaskan melalui bibir Michel Ardan dan Barbicane:"Apakah Anda tahu, Barbicane, apa yang telah saya pikirkan sepanjang malam?"
Henri Garcet (1815–1871)Namun, kita mungkin tidak akan tahu tentang perhitungannya jika Jules Verne tidak menempatkannya di awal buku "Around the Moon", menggunakannya dalam percakapan para kru kerang Columbiada. Mereka menulis bahwa pembaca surat kabar "Debat" tertanggal 7 November 1869 benar-benar kagum melihat perhitungan matematika yang rumit - penerbitan novel dimulai di surat kabar ini.Beginilah model matematika dari penerbangan itu dijelaskan melalui bibir Michel Ardan dan Barbicane:"Apakah Anda tahu, Barbicane, apa yang telah saya pikirkan sepanjang malam?"
- Bagaimana dengan? Ketua bertanya.
— . , , , . : , , , .
— , — , — , , , , , .
— , , — .- - ?
— .
— ?
…
"Ya, teman baik." Mempertimbangkan semua kondisi masalah yang diketahui:
jarak dari pusat bumi ke pusat bulan, jari-jari bumi, massa bumi, massa bulan, saya dapat secara akurat menentukan kecepatan awal proyektil kita, dan pada saat yang sama menggunakan rumus paling sederhana.
- Apa rumusnya?
- Tapi kamu tahu. Tapi hanya saya yang tidak akan mencoret kurva yang digambarkan oleh cangkang kami antara Bulan dan Bumi, mengingat gerakan relatif mereka di sekitar Matahari. Misalkan kedua planet tidak bergerak. Itu sudah cukup.
- Kenapa?
- Karena ini adalah bagaimana tugas yang disebut "tugas tiga tubuh" diselesaikan, metode integral untuk memecahkan masalah seperti itu belum cukup dikembangkan.Setelah beberapa saat, formula juga diperkenalkan, yang disajikan kepada pembaca:dimana r adalah jari-jari Bumi, adalah jarak antara pusat Bumi dan Bulan, x adalah jarak inti dari Bumi. V 0 adalah kecepatan awal inti. V adalah kecepatan pada jarak x.Dan penerbangannya terlihat seperti iniDi sini saya ingin mencatat bahwa rumus ini dengan data awal yang ditunjukkan memang benar. Dan itu benar-benar secara akurat menampilkan efek gravitasi Bumi dan Bulan pada perangkat pada waktu tertentu. Cukup mudah untuk diturunkan dari hukum kekekalan energi.Penurunan rumus Verne-Garce
mv2 / 2 – γMm/R – γMm/R =const
m M,M – , ,
γ – , R - , R-
. .
mv2 / 2 – γMm/x– γMm/(D-x) =mv02 / 2 – γMm/r – γMm/(d-r)
m,
v2 / 2 –v02 / 2=γM/x+ γM/(D-x)– γM/r – γM/(d-r)
1/2*(v2-v02 )=γM(1/-1/r+M/M*1/(d-x)-M/M*1/(d-r))
1/2*(v2-v02 )=γM/r(r/-1+M/M(r/(d-x)-r/(d-r))
mg=mγM/r2 γM=g*r2
1/2*(v2-v02 )=gr(r/-1+M/M(r/(d-x)-r/(d-r))
Jadi apa masalahnya? Masalahnya adalah itu tidak memperhitungkan dinamika sistem. Bulan berputar mengelilingi Bumi dengan kecepatan sekitar 1 km / s. Inilah masalah dari masalah ini. Akibatnya, ketika mencoba terbang sesuai dengan skema di atas, ketika stasiun terbang ke titik netral antara Bumi dan Bulan, itu tidak akan ditangkap sama sekali oleh medan Bulan, karena yang terakhir akan terbang jauh dari proyektil dengan kecepatan satu kilometer per detik, dan proyektil akan mulai jatuh ke Bumi. Tapi kemudian ada harapan bahwa penangkapan perangkat oleh Bulan akan tetap terjadi, dan skema yang sama, dengan perkiraan pertama, secara akurat menunjukkan dinamika penerbangan. Dengan tangan ringan Jules Verne, metode perhitungan penerbangan yang serupa segera menjadi sangat populer. Itu mulai digunakan tidak hanya dalam buku-buku seni, tetapi juga dalam karya ilmiah yang serius.Perlu dicatat bahwa kemudian para astronom hanya memahami pentingnya memperhitungkan dinamika. Ya, dan persamaan diferensial yang memperhitungkan gravitasi dan dinamika, maka dapat dengan mudah disusun. Hanya saja tidak dapat menemukan solusi sederhana. Sebenarnya, seperti yang sekarang dipahami dengan baik, masalah tiga-tubuh tidak memiliki solusi analitis umum. Masalahnya dapat diselesaikan hanya secara numerik, yang berarti sangat banyak perhitungan rutin, yang dapat menghabiskan waktu berbulan-bulan atau bahkan bertahun-tahun. Pada saat penerbitan novel, masalah yang sama diselesaikan secara numerik hanya dua kali. Selain itu, upaya pertama adalah lebih dari seratus tahun sebelum penerbitan novel, pada 1759.Diketahui bahwa Edmund Halley, yang menyusun katalog komet, memperhatikan bahwa beberapa komet yang muncul di langit pada waktu yang berbeda memiliki parameter yang sangat mirip. Setelah memverifikasi mereka, ia memutuskan bahwa itu mungkin komet yang sama. Maka dia akan dipanggil dengan namanya. Komet Halley muncul di langit pada 1531, 1607 dan 1682. Artinya, periode sirkulasi adalah 75-76 tahun, dan ilmuwan memprediksikan penampilan berikutnya untuk 1758. Dan semuanya akan luar biasa, jika bukan karena satu "tetapi": pada perkiraan waktu, komet di langit tidak pernah muncul.Kemudian ahli matematika Prancis, Cleo memutuskan untuk menghitung lintasannya seakurat mungkin. Termasuk, dengan mempertimbangkan gangguan lintasannya karena daya tarik Jupiter dan Saturnus. Itu adalah pekerjaan yang sangat melelahkan dan panjang, meskipun dia tidak melakukan pekerjaan ini sendirian: dia dibantu oleh astronom J. Lalande dan ahli matematika Madame Lepot. Ternyata perbedaan dengan perkiraan sebelumnya dari periode revolusi komet adalah 618 hari, dan akan tiba pada perihelionnya pada 13 April 1759. Dengan kemungkinan kesalahan selama sebulan. Penilaian itu ternyata sangat akurat: komet itu lulus perihelion pada 12 Maret. Itu adalah kemenangan bagi matematikawan dan konfirmasi yang sangat baik dari hukum Newton.Tentang perhitungan ini, Laland kemudian menulis: "Kami menghitung enam bulan dari pagi hingga malam, kadang-kadang tanpa melihat dari makanan, dan konsekuensi dari hal ini adalah saya mengganggu kesehatan saya selama sisa hidup saya. Bantuan Madame Lepot sedemikian rupa sehingga tanpa dia kita tidak akan pernah berani melakukan pekerjaan besar ini, yang terdiri dari menghitung jarak komet dari dua planet - Jupiter dan Saturnus - untuk setiap tingkat bidang langit selama 150 tahun. "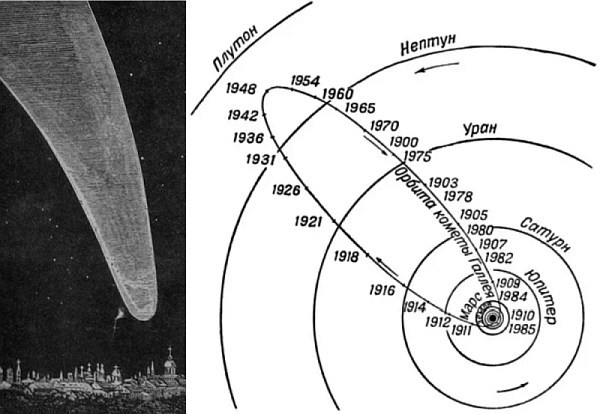 Anda dapat melihat lintasan komet Halley relatif terhadap orbitnya. planetKedua kalinya metode yang sama digunakan pada tahun 1829, sekali lagi ketika menghitung lintasan komet Halley. Perkiraan memberikan tanggal komet kembali ke Matahari pada 15 November 1835. Komet kembali pada 16 November, hanya terlambat satu hari.Hasilnya, metode numerik yang serupa telah membuktikan akurasinya. Tetapi dari cerita di atas, Anda dapat dengan jelas melihat berapa banyak dan pekerjaan yang membosankan diperlukan. Enam bulan kerja dari tiga matematikawan perlu menghitung hanya satu lintasan dengan parameter awal yang terkenal! Tetapi untuk menghitung lintasan penerbangan dari Bumi ke Bulan, perlu untuk mengevaluasi lusinan, jika bukan ratusan lintasan, dengan parameter awal yang berbeda. Kalau tidak, tidak mungkin untuk mendapatkan, katakanlah, kecepatan yang tepat, tanggal peluncuran, karakteristik lintasan, kemungkinan kesalahan, parameter penerbangan stasiun dekat bulan, dll. Ini bisa memakan waktu bertahun-tahun. Artinya, solusi ini dianggap sangat sulit. Terutama untuk tugas yang tidak berarti banyak praktis.Pada saat yang sama, ada juga kepercayaan bahwa solusi analitis untuk masalah tiga tubuh dapat ditemukan. Setidaknya memungkinkan, dalam perkiraan pertama, untuk mengevaluasi parameter penerbangan.Dan metode yang diusulkan oleh Jules Verne tampaknya memberikan jawaban untuk pertanyaan ini. Bagaimanapun, secara matematis, dalam kerangka asumsi awal, ia sempurna. Ya, dia tidak memperhitungkan dinamika, tetapi kemudian banyak yang menduga bahwa asumsi ini normal, dan lintasan nyata proyektil dari Bumi ke Bulan akan terlihat seperti ini.Perhitungan dari buku “Pesawat Luar Angkasa. (Komunikasi antarplanet dalam fantasi para novelis) ”1928Dan keindahan matematika, ditambah dengan popularitas besar novel, memainkan lelucon yang kejam: menggunakan metode ini, praktis semua pelopor eksplorasi ruang angkasa - Goddard , Sternfeld , Obert , Max Valle dan banyak lainnya - mengevaluasi penerbangan . Terkadang, sangat jarang, mereka juga memperkirakan bukan penerbangan langsung, tetapi oleh elips dari satelit Bumi. Tetapi metode ini juga memiliki kekurangan. Sebagai contoh, untuk beberapa alasan banyak yang yakin bahwa untuk mencapai bulan itu cukup untuk jatuh ke dalam lingkup tindakannya; lebih lanjut, kata mereka, daya tarik bulan harus melakukan sisanya. Meskipun, seperti yang dikatakan di atas, kemungkinan terbang di dalam masalah tiga tubuh telah terbukti.Ilustrasi yang baik adalah artikel Werner von Braun dalam jurnal mingguan 18 Oktober 1952, di mana von Braun menggambarkan bagaimana, menurut pendapatnya, sebuah ekspedisi ke bulan akan terlihat seperti.
Anda dapat melihat lintasan komet Halley relatif terhadap orbitnya. planetKedua kalinya metode yang sama digunakan pada tahun 1829, sekali lagi ketika menghitung lintasan komet Halley. Perkiraan memberikan tanggal komet kembali ke Matahari pada 15 November 1835. Komet kembali pada 16 November, hanya terlambat satu hari.Hasilnya, metode numerik yang serupa telah membuktikan akurasinya. Tetapi dari cerita di atas, Anda dapat dengan jelas melihat berapa banyak dan pekerjaan yang membosankan diperlukan. Enam bulan kerja dari tiga matematikawan perlu menghitung hanya satu lintasan dengan parameter awal yang terkenal! Tetapi untuk menghitung lintasan penerbangan dari Bumi ke Bulan, perlu untuk mengevaluasi lusinan, jika bukan ratusan lintasan, dengan parameter awal yang berbeda. Kalau tidak, tidak mungkin untuk mendapatkan, katakanlah, kecepatan yang tepat, tanggal peluncuran, karakteristik lintasan, kemungkinan kesalahan, parameter penerbangan stasiun dekat bulan, dll. Ini bisa memakan waktu bertahun-tahun. Artinya, solusi ini dianggap sangat sulit. Terutama untuk tugas yang tidak berarti banyak praktis.Pada saat yang sama, ada juga kepercayaan bahwa solusi analitis untuk masalah tiga tubuh dapat ditemukan. Setidaknya memungkinkan, dalam perkiraan pertama, untuk mengevaluasi parameter penerbangan.Dan metode yang diusulkan oleh Jules Verne tampaknya memberikan jawaban untuk pertanyaan ini. Bagaimanapun, secara matematis, dalam kerangka asumsi awal, ia sempurna. Ya, dia tidak memperhitungkan dinamika, tetapi kemudian banyak yang menduga bahwa asumsi ini normal, dan lintasan nyata proyektil dari Bumi ke Bulan akan terlihat seperti ini.Perhitungan dari buku “Pesawat Luar Angkasa. (Komunikasi antarplanet dalam fantasi para novelis) ”1928Dan keindahan matematika, ditambah dengan popularitas besar novel, memainkan lelucon yang kejam: menggunakan metode ini, praktis semua pelopor eksplorasi ruang angkasa - Goddard , Sternfeld , Obert , Max Valle dan banyak lainnya - mengevaluasi penerbangan . Terkadang, sangat jarang, mereka juga memperkirakan bukan penerbangan langsung, tetapi oleh elips dari satelit Bumi. Tetapi metode ini juga memiliki kekurangan. Sebagai contoh, untuk beberapa alasan banyak yang yakin bahwa untuk mencapai bulan itu cukup untuk jatuh ke dalam lingkup tindakannya; lebih lanjut, kata mereka, daya tarik bulan harus melakukan sisanya. Meskipun, seperti yang dikatakan di atas, kemungkinan terbang di dalam masalah tiga tubuh telah terbukti.Ilustrasi yang baik adalah artikel Werner von Braun dalam jurnal mingguan 18 Oktober 1952, di mana von Braun menggambarkan bagaimana, menurut pendapatnya, sebuah ekspedisi ke bulan akan terlihat seperti.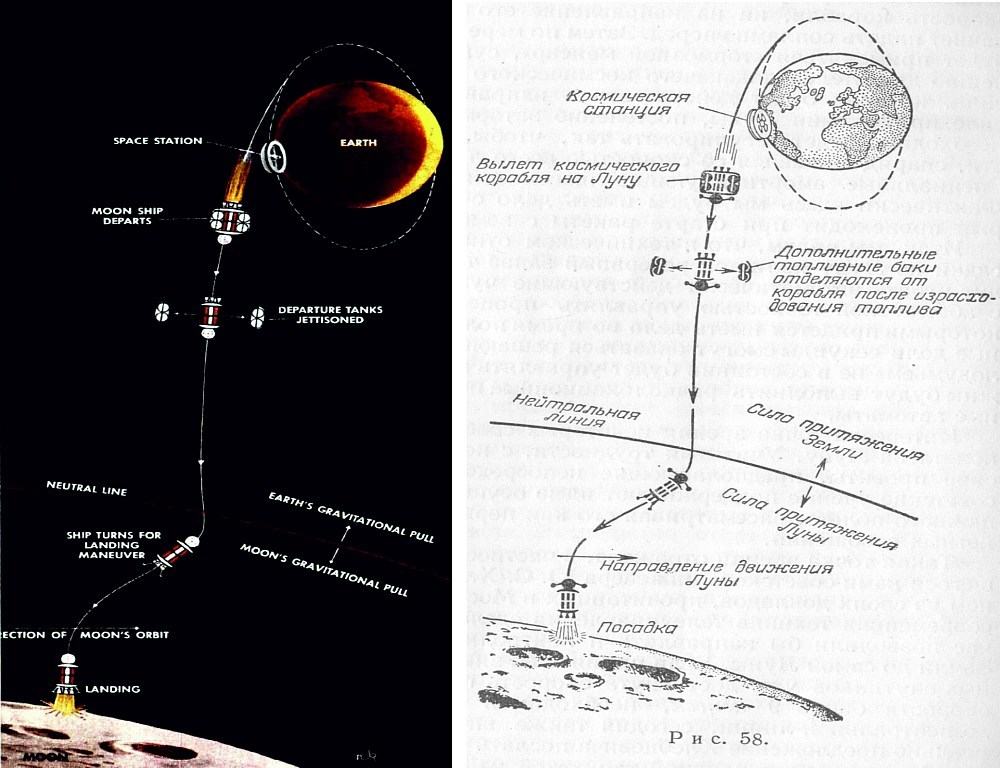
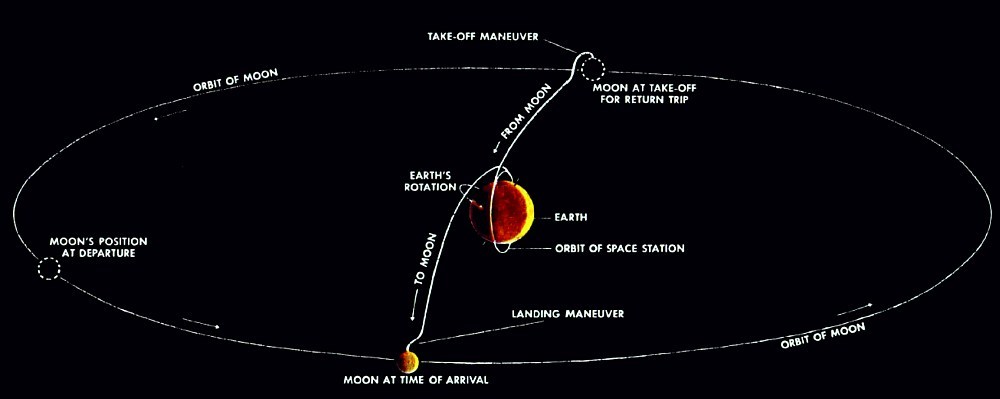 Artikel itu sendiri dapat diunduh di sini.Dari ilustrasi itu terlihat jelas bahwa justru skema Jules Verne yang disajikan di sana: pertama, mencapai wilayah netral antara Bumi dan Bulan, dan kemudian jatuh ke Bulan di bawah pengaruh daya tariknya. Meriam telah lama digantikan oleh roket, tetapi prinsip dasarnya tetap tidak berubah. Meskipun hampir seratus tahun telah berlalu sejak penerbitan novel.Namun segera pendekatan penerbangan dari Bumi ke Bulan mulai berubah. Termasuk, berkat perkembangan komputer elektronik.Kelanjutan berikut .
Artikel itu sendiri dapat diunduh di sini.Dari ilustrasi itu terlihat jelas bahwa justru skema Jules Verne yang disajikan di sana: pertama, mencapai wilayah netral antara Bumi dan Bulan, dan kemudian jatuh ke Bulan di bawah pengaruh daya tariknya. Meriam telah lama digantikan oleh roket, tetapi prinsip dasarnya tetap tidak berubah. Meskipun hampir seratus tahun telah berlalu sejak penerbitan novel.Namun segera pendekatan penerbangan dari Bumi ke Bulan mulai berubah. Termasuk, berkat perkembangan komputer elektronik.Kelanjutan berikut .