Pada bulan November, majalah Quanta membingungkan para pembacanya dengan pertanyaan-pertanyaan tentang menggambar bentuk-bentuk dari benda datar yang identik (seperti koin atau kartu domino). Artikel ini memberikan pertanyaan dan jawaban terinci untuk mereka.Pertanyaan 1
, , . . . , , ? n ?
Secara fisik, tugas tersebut membutuhkan keseimbangan torsi gambar di kedua sisi tepi meja. Torsi masing-masing sisi adalah produk dari massa sisi ini dan jarak dari pusat massa ke tepi. Ketika pusat massa seluruh gambar berada di atas tepi, momen yang sama bekerja di kedua sisi, dan torsi sistem total adalah nol. Untuk objek majemuk, total torsi untuk setiap wajah dapat ditemukan dengan menambahkan torsi semua komponen. Oleh karena itu, kita dapat membagi dan mengatur tugas asli, hanya mempertimbangkan perubahan yang terjadi ketika blok baru ditambahkan ke tumpukan yang ada, sesuatu seperti induksi matematika (sebut saja induksi fisik).Pertimbangkan tumpukan blok n-1, yang masing-masing beratnya satu unit berat dan memiliki panjang satu unit panjang. Tumpukan seimbang di ujung meja. Bayangkan bahwa garis penglihatan diarahkan di sepanjang tepi meja, dan meja di sebelah kiri - yaitu, ujung gantung balok menjulur ke kanan. Karena tumpukan seimbang di tepi, pusat massa tepat di atas tepi, dan torsinya nol. Sekarang bayangkan bahwa kita mengangkat seluruh tumpukan secara vertikal, dan menempatkan blok lain di bawahnya sehingga ujung kanannya rata dengan ujung meja. Dalam praktiknya, ini bisa sulit, tetapi dalam eksperimen pikiran itu sederhana.Kami menambahkan beberapa stabilitas ke tumpukan dengan menambahkan blok ke-n dari bawah, karena pusat massa seluruh tumpukan sedikit bergeser ke kiri. Nyatakan offset ini x. n blok berbobot n unit, dan mereka memiliki torsi umum x * n di sekitar tepi meja, diarahkan ke kiri. Ingat bahwa tumpukan blok n-1 memiliki momen nol total. Kami hanya menambahkan momen dari blok baru - dengan massa satu unit massa dan dengan jarak ke pusat massa dari tepi meja menjadi setengah unit panjangnya.Ternyata x * n = 1/2, yang berarti x = 1 / 2n, di mana x adalah jarak ke pusat massa baru dari tepi tabel.Ini berarti bahwa jika Anda memindahkan seluruh tumpukan n blok ke kanan dengan panjang 1/2, itu akan seimbang sempurna di tepi - dan ini adalah pergeseran maksimum yang mungkin. Untuk menyelesaikan konstruksi induksi, kami mencatat bahwa overhang maksimum blok pertama dari tepi tabel adalah 1/2 unit panjangnya.Oleh karena itu, untuk lima blok, kami mengganti formula n untuk setiap level dari 1 hingga lima untuk mendapatkan overhang maksimum:x=1/2+1/4+1/6+1/8+1/10=137/120=1,141(6)
Dapat dilihat bahwa jika Anda mulai dari atas dan kemudian menambahkan blok ke bawah, setiap shift akan menjadi setengah dari kebalikan dari jumlah blok yang tersedia. Urutan angka terbalik seperti itu dikenal sebagai seri harmonik. Serangkaian seperti itu perlahan-lahan menyimpang, dan karena n cenderung tak terhingga, ia juga cenderung tak terhingga.Rumus penjumlahan umum untuk n blok diperoleh dengan menjumlahkan semua anggota seri. Ternyata setengah dari istilah harmonik ke-n, yang dapat ditulis sebagai:Pertanyaan 2
Bayangkan Anda memiliki lima balok yang sama, dan Anda ingin meletakkan hiasan di atasnya, pada titik yang panjangnya seperempat panjang balok dari ujung yang menggantung. Semua balok memiliki berat satu unit, dan perhiasan memiliki berat seperlima dari balok. Berapa panjang maksimum overhang sekarang? Bagaimana ini mengubah formula dasar?
Pertama, perhatikan balok pertama dengan hiasan berdiri di atasnya, dan berbaring sehingga ujung kanannya rata dengan tepi meja. Pusat massa balok tanpa dekorasi adalah setengah unit panjangnya dari tepi meja. Dekorasi akan memindahkannya ke kanan, katakanlah, x. Massa dekorasi 1/5, dan jaraknya dari pusat massa baru adalah 1/4. Kami menyamakan momen dan mendapatkan x = 1/5 * (1/4 x), oleh karena itu, x = 1/24. Karena dekorasi, perlu untuk memindahkan blok pertama ke kiri 1/24 panjangnya, sehingga overhang maksimum sekarang 11/24 bukan 1/2.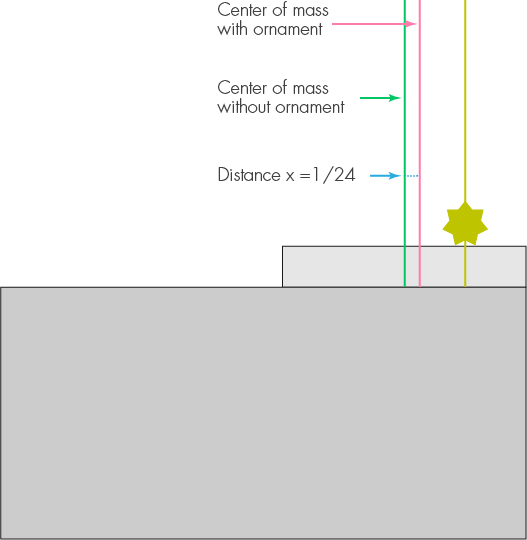
Pertanyaan 3
, , . . . , . , , . , ?
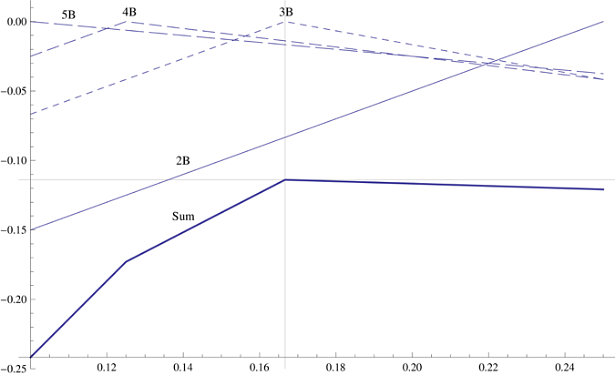
Karena probabilitas memiliki dua hingga lima blok adalah sama, Anda perlu memaksimalkan jumlah yang menunjukkan overhang maksimum untuk empat kasus ini. Untuk tumpukan 2-5 blok, ada posisi optimal dari blok pertama, memberikan overhang maksimum dari seluruh tumpukan. Jika Anda membuat overhang terbesar pada grafik untuk masing-masing dari empat ukuran yang mungkin dari tumpukan berikutnya, Anda mendapatkan dua grafik garis dan dua grafik dalam bentuk V. terbalik. Simpul mereka menunjukkan posisi awal optimal dari blok awal untuk tumpukan 3-4 blok. Merangkum grafik, kita mendapatkan grafik overhang keseluruhan, yang secara dramatis mengubah arah di masing-masing dari empat posisi optimal. Ternyata overhang keseluruhan terbaik dicapai pada posisi optimal untuk tiga blok, setelah itu grafik turun. Karena itu, Anda perlu menempatkan blok asli di bawah asumsiAnda akan diberikan tiga blok tambahan, dan overhang akan 1/6 unit panjangnya.