70 tahun yang lalu, pada 16 Desember 1947, di laboratorium Bell Labs, John Bardin dan Walter Brattain, di bawah arahan William Shockley, menciptakan transistor bipolar operasional pertama. Pada 23 Desember, Brattain mendemonstrasikan penguat transistor pertama kepada rekan-rekannya. Karena itu, hari ini sering disebut Transistor Day . Tidak perlu berbicara tentang pentingnya acara ini. Transistor dianggap sebagai salah satu penemuan paling penting dari abad ke-20, yang tanpanya komputer akan tetap bekerja pada lampu dan relay, dan menempati seluruh bangunan. Shockley, Bardin, dan Brattain menerima Hadiah Nobel Fisika untuk pekerjaan mereka pada tahun 1956. Selama bertahun-tahun, transistor telah miniatur menjadi hanya beberapa atom. Setiap prosesor memiliki milyaran transistor, sehingga transistor dapat disebut perangkat paling masif yang dibuat oleh umat manusia.Tapi pekerjaan apa yang dilakukan transistor untuk kita? Mari kita melakukan perjalanan mental: kita akan melacak jalur dari beberapa ujung jari tinggi ke ulang tahun kita - transistor.Apa yang harus diambil sebagai titik awal? Yah, setidaknya gambar tombol habrakat.
Tidak perlu berbicara tentang pentingnya acara ini. Transistor dianggap sebagai salah satu penemuan paling penting dari abad ke-20, yang tanpanya komputer akan tetap bekerja pada lampu dan relay, dan menempati seluruh bangunan. Shockley, Bardin, dan Brattain menerima Hadiah Nobel Fisika untuk pekerjaan mereka pada tahun 1956. Selama bertahun-tahun, transistor telah miniatur menjadi hanya beberapa atom. Setiap prosesor memiliki milyaran transistor, sehingga transistor dapat disebut perangkat paling masif yang dibuat oleh umat manusia.Tapi pekerjaan apa yang dilakukan transistor untuk kita? Mari kita melakukan perjalanan mental: kita akan melacak jalur dari beberapa ujung jari tinggi ke ulang tahun kita - transistor.Apa yang harus diambil sebagai titik awal? Yah, setidaknya gambar tombol habrakat.HTML dan CSS
Tombol terdiri dari piksel latar belakang, teks, dan batas. Dalam kode, disetel oleh tag <a>, yang menerapkan aturan tata letak CSS. Misalnya, aturan CSS diterapkan ke perbatasan ke sudut-sudut:border-radius: 3px;
 Dengan demikian, batas terdiri dari empat segmen dan empat busur ("perempat" dari sebuah lingkaran).
Dengan demikian, batas terdiri dari empat segmen dan empat busur ("perempat" dari sebuah lingkaran).Browser
Untuk penelitian, saya mengambil Firefox favorit saya. Sebelum FF mulai menggambar tombol kita, dia perlu melakukan banyak pekerjaan untuk mem-parsing dan menghitung posisi elemen:- Unduh HTML melalui jaringan, parse, buat pohon DOM
- Unduh melalui jaringan CSS, lakukan analisis leksikal, parse
- Bind aturan berdasarkan prioritas dan pewarisan elemen halaman
- Untuk semua node DOM yang terlihat, buat pohon area persegi panjangnya - bingkai.
- Untuk bingkai, hitung dimensi dan lokasi (lihat video )
- Buat layer dari bingkai dengan mempertimbangkan indeks-z dan tipe konten (<canvas>, SVG, <video>).
- Buat daftar gambar secara berurutan: warna latar belakang, gambar latar belakang, batas, keturunan, garis besar.
Kami tidak akan membahas langkah-langkah ini secara rinci. Setelah itu muncul gambar sebenarnya dari elemen-elemen yang diperlukan.Unduh sumbernya untuk mencari tahu apa yang terjadi di sana,Mozilla Firefox.
Firefox Mercurial Visual Studio C++. VS
symbols.mozilla.org. - /layout/.
, , , Firefox. c , , — FF.
File nsCSSRenderingBorders.cpp bertanggung jawab untuk menggambar batas . Dan fungsi umum menggambar batas disebut (siapa yang menyangka): DrawBorders () . Fungsi memilih metode rendering optimal untuk berbagai situasi. Kami memiliki kasus yang relatif sederhana: ada batas-jari-jari, tetapi batas di semua sisi solid dan berwarna sama.Kami jikaif (allBordersSame &&
mCompositeColors[0] == nullptr &&
mBorderStyles[0] == NS_STYLE_BORDER_STYLE_SOLID &&
!mAvoidStroke &&
!mNoBorderRadius)
{
gfxRect outerRect = ThebesRect(mOuterRect);
RoundedRect borderInnerRect(outerRect, mBorderRadii);
borderInnerRect.Deflate(mBorderWidths[eSideTop],
mBorderWidths[eSideBottom],
mBorderWidths[eSideLeft],
mBorderWidths[eSideRight]);
RefPtr<PathBuilder> builder = mDrawTarget->CreatePathBuilder();
AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
return;
}
Ada opsi yang jauh lebih kompleks, seperti docking di sudut-sudut dengan jari-jari perbatasan dari berbagai jenis garis putus-putus dan putus-putus, lihat DrawDashedOrDottedCorner () . Ada dalam kode sepenuhnyaTapi kembali ke if kita. Dari komentar kita belajar bahwa dalam hal ini perbatasan ditarik menggunakan dua persegi panjang - internal dan eksternal, maka jalur yang dibuat (path) diisi dengan warna yang diinginkan.AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
Pergi ke AppendRoundedRectToPath () di gfx / 2d / PathHelpers.cpp.Sekali lagi kita atur breakpoints Kita belajar dari komentar tentang fungsi bahwa sudut-sudut digambar di empat titik kontrol oleh kurva Bezier . Kurva Bezier sering digunakan dalam grafik komputer, termasuk untuk menggambar busur lingkaran dan elips. Ketika kita belajar lebih jauh dari komentar, ada banyak opsi untuk memilih titik kontrol untuk membuat kurva. Dalam hal ini, kita perlu bahwa titik 0 dan 3 milik sisi persegi panjang, titik 0, 1 dan C terletak pada satu garis lurus, titik 3, 2 dan C di sisi lainnya. Lihat gambar: Tetap bagi kami untuk menghitung rasio panjang segmen 01 / 0C dan 32 / 3C. Di sini penulis menggunakan perkiraan perhitungan dan mendapatkan alpha konstanta ajaib:
Tetap bagi kami untuk menghitung rasio panjang segmen 01 / 0C dan 32 / 3C. Di sini penulis menggunakan perkiraan perhitungan dan mendapatkan alpha konstanta ajaib:const Float alpha = Float(0.55191497064665766025);
Sayangnya, artikel dengan algoritma pemilihan pos pemeriksaan yang dirujuk oleh komentar tidak ada dalam domain publik. Tetapi secara umum, perlu dicatat bahwa dalam grafik komputer, algoritma sering menggunakan pendekatan untuk meningkatkan kinerja. Misalnya, algoritma Brezenham memungkinkan Anda untuk menggambar segmen dan lingkaran bukan “di dahi” - dengan menyelesaikan persamaan y = f (x), tetapi dengan operasi integer yang lebih licik. Hal yang sama dengan isi, dll.Lebih jauh dalam siklus kita pergi dari sudut ke sudut, gunakan alpha untuk menghitung koordinat titik kontrol dan, akhirnya, memanggil fungsi menggambar garis perbatasan dan lengkungan sudut:aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
Kode AppendRoundedRectToPath () lengkapvoid
AppendRoundedRectToPath(PathBuilder* aPathBuilder,
const Rect& aRect,
const RectCornerRadii& aRadii,
bool aDrawClockwise)
{
const Float alpha = Float(0.55191497064665766025);
typedef struct { Float a, b; } twoFloats;
twoFloats cwCornerMults[4] = { { -1, 0 },
{ 0, -1 },
{ +1, 0 },
{ 0, +1 } };
twoFloats ccwCornerMults[4] = { { +1, 0 },
{ 0, -1 },
{ -1, 0 },
{ 0, +1 } };
twoFloats *cornerMults = aDrawClockwise ? cwCornerMults : ccwCornerMults;
Point cornerCoords[] = { aRect.TopLeft(), aRect.TopRight(),
aRect.BottomRight(), aRect.BottomLeft() };
Point pc, p0, p1, p2, p3;
if (aDrawClockwise) {
aPathBuilder->MoveTo(Point(aRect.X() + aRadii[RectCorner::TopLeft].width,
aRect.Y()));
} else {
aPathBuilder->MoveTo(Point(aRect.X() + aRect.Width() - aRadii[RectCorner::TopRight].width,
aRect.Y()));
}
for (int i = 0; i < 4; ++i) {
int c = aDrawClockwise ? ((i+1) % 4) : ((4-i) % 4);
int i2 = (i+2) % 4;
int i3 = (i+3) % 4;
pc = cornerCoords[c];
if (aRadii[c].width > 0.0 && aRadii[c].height > 0.0) {
p0.x = pc.x + cornerMults[i].a * aRadii[c].width;
p0.y = pc.y + cornerMults[i].b * aRadii[c].height;
p3.x = pc.x + cornerMults[i3].a * aRadii[c].width;
p3.y = pc.y + cornerMults[i3].b * aRadii[c].height;
p1.x = p0.x + alpha * cornerMults[i2].a * aRadii[c].width;
p1.y = p0.y + alpha * cornerMults[i2].b * aRadii[c].height;
p2.x = p3.x - alpha * cornerMults[i3].a * aRadii[c].width;
p2.y = p3.y - alpha * cornerMults[i3].b * aRadii[c].height;
aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
} else {
aPathBuilder->LineTo(pc);
}
}
aPathBuilder->Close();
}
Tapi kemudian itu semua tergantung pada backend dari grafik 2D yang digunakan Mozilla.Mesin grafis
Gecko menggunakan pustaka Moz2D platform-independen, yang pada gilirannya dapat menggunakan salah satu backend: Kairo, Skia, Direct2D, Quartz dan NV Path. Misalnya, Direct2D, Kairo, Skia tersedia untuk Windows. Skia juga merupakan backend Chromium. Anda dapat mengubah backend di about: config. Backend, pada gilirannya, dapat membaca semua yang ada di CPU, atau mereka dapat menggunakan akselerasi perangkat keras GPU sampai batas tertentu. Sebagai contoh, Skia memiliki backend OpenGL sendiri - Ganesh.Kode Direct2D ditutup, jadi sebaiknya kita nyalakan Skia dan lihat apa fungsinya. Fungsi untuk menggambar kurva kubik SkPath :: cubicTo disebut. Untuk membuat kurva, kurva ini dibagi oleh algoritma de Castelljo menjadi sejumlah segmen lurus, yang sebenarnya digambar (lihat core / SkGeometry.cpp).Kode mesin
Sejujurnya, saya tidak berhasil sepenuhnya memahami internal Skia, jadi saya mengambil langkah mundur - ke AppendRoundedRectToPath (), di mana semua operasi dilakukan pada bilangan bulat - yang mana bisa lebih mudah?Setelah membuka kode yang dibongkar, kita harus menemukan operasi penambahan di dalamnya....
142B1863 00 00 add byte ptr [eax],al
142B1865 00 8D 43 FF 0F 84 add byte ptr [ebp-7BF000BDh],cl
142B186B 67 01 00 add dword ptr [bx+si],eax
142B186E 00 99 0F 57 C9 F7 add byte ptr [ecx-836A8F1h],bl
142B1874 F9 stc
142B1875 8B C3 mov eax,ebx
142B1877 8B CA mov ecx,edx
142B1879 99 cdq
142B187A F7 7C 24 28 idiv eax,dword ptr [esp+28h]
...
Ya! Bahkan seseorang yang jauh dari ASM seperti saya dapat dengan mudah menebak bahwa operasi ADD bertanggung jawab untuk penambahan. Ambil operasi pertama:142B1863 00 00 add byte ptr [eax],al0x142B1863 - alamat di RAM0x00 - opcode - kode instruksi prosesor. Mozilla ini dikompilasi di bawah x86, dan membuka tabel instruksi x86 , kita akan melihat bahwa kode 00 berarti operasi penambahan 8-bit dengan ADD mnemonics. Operan pertama dapat berupa register atau sel memori akses acak, yang kedua dapat berupa register. Operan pertama ditambahkan ke yang kedua, hasilnya ditulis ke yang pertama. Saya akan menjelaskan, untuk jaga-jaga, bahwa register adalah memori ultrafast RAM di dalam prosesor, misalnya, untuk menyimpan hasil perhitungan menengah.Byte kedua juga 0x00 dan disebut MOD-REG-R / M. Bitnya menentukan operan dan metode pengalamatan. MOD = 00b dalam kombinasi dengan R / M = 000b berarti bahwa pengalamatan tidak langsung digunakanREG = 000b berarti bahwa register AL digunakan (8-bit yang lebih rendah dari register EAX)[eax] - menunjukkan bahwa penambahan dibuat dengan sel RAM, yang alamatnya ada di register EAX.Bagaimanaprosesor memproses perintah ADD?
MOD = 00b dalam kombinasi dengan R / M = 000b berarti bahwa pengalamatan tidak langsung digunakanREG = 000b berarti bahwa register AL digunakan (8-bit yang lebih rendah dari register EAX)[eax] - menunjukkan bahwa penambahan dibuat dengan sel RAM, yang alamatnya ada di register EAX.Bagaimanaprosesor memproses perintah ADD?CPU
Berdasarkan uraian mikroarsitektur Skylake , saya menyusun daftar langkah (yang sangat disederhanakan):- Instruksi X86 diambil dari cache instruksi L1 32KB menjadi buffer precoding 16-byte
- Perintah yang sudah dikodekan diatur dalam Instruksi Antrian (berukuran 2x25) dan masuk ke dalam decoder
- x86 1-4 (µOPs). ADD 1 µOP ALU (- ) 2 µOP AGU ( ) (., ). 86 .
- Allocation Queue (IDQ). , Loop Stream Detector — .
- : , . . .
- Mikrooperasi pergi ke manajer Penjadwal Bersatu, yang memutuskan pada titik apa dan di mana pelabuhan untuk mengirim operasi untuk dieksekusi di luar urutan penerimaan. Di belakang setiap port adalah aktuator. Operasi mikro kami akan menuju ke ALU dan AGU.
 Inti dari SkyLake. Gambar dari en.wikichip.org .Saya ulangi, ini adalah deskripsi saya yang sangat sederhana dan tidak berpura-pura akurat dan lengkap. Untuk referensi lebih lanjut, saya sarankan membaca posting Journey Through the Processor Processor Processor dan artikel Processors dari Intel Core i7 Family
Inti dari SkyLake. Gambar dari en.wikichip.org .Saya ulangi, ini adalah deskripsi saya yang sangat sederhana dan tidak berpura-pura akurat dan lengkap. Untuk referensi lebih lanjut, saya sarankan membaca posting Journey Through the Processor Processor Processor dan artikel Processors dari Intel Core i7 FamilyALU
Sekarang akan menarik untuk mengetahui apa yang terjadi di ALU: bagaimana angka-angkanya ditambahkan? Sayangnya, informasi tentang implementasi spesifik arsitektur mikro dan ALU adalah rahasia dagang Intel, jadi kami beralih ke teori nanti.Perangkat untuk menambahkan dua bit biner (mis. Bit) disebut adder . Outputnya adalah jumlah dan jumlah bit. Sumber: WikipediaSejak dalam kehidupan nyata, kita perlu menambahkan angka yang terdiri dari beberapa digit, penambah juga harus menerima bit carry dari digit sebelumnya sebagai input. Adder semacam itu disebut penuh .
Sumber: WikipediaSejak dalam kehidupan nyata, kita perlu menambahkan angka yang terdiri dari beberapa digit, penambah juga harus menerima bit carry dari digit sebelumnya sebagai input. Adder semacam itu disebut penuh .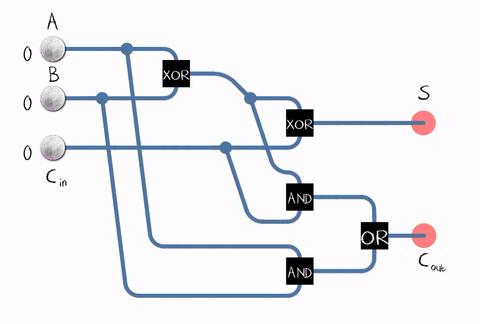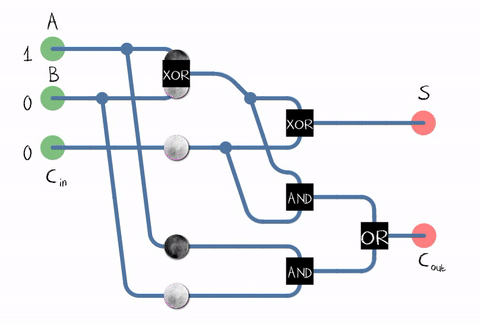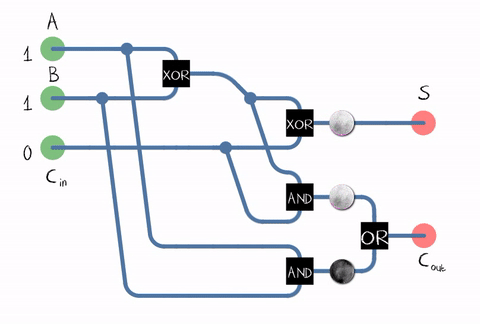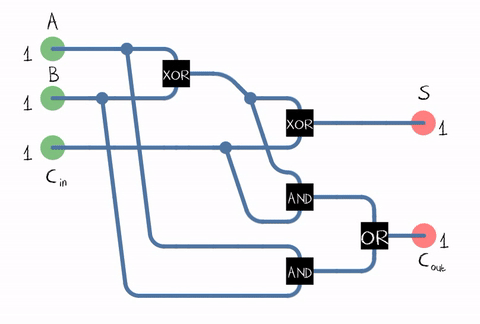 Sumber: WikipediaSeperti dapat dilihat dari gambar, penambah terdiri dari elemen logika: XOR, AND, OR. Dan setiap elemen logisdapat diimplementasikan menggunakan beberapa transistor. Atau bahkan estafet .
Sumber: WikipediaSeperti dapat dilihat dari gambar, penambah terdiri dari elemen logika: XOR, AND, OR. Dan setiap elemen logisdapat diimplementasikan menggunakan beberapa transistor. Atau bahkan estafet . Contoh penerapan penambah penuh pada transistor CMOS . SumberJadi kita sampai ke transistor! Meskipun, tentu saja, tidak hanya ALU bekerja pada transistor, tetapi juga unit prosesor lainnya, tetapi sebagian besar transistor digunakan dalam cache sebagai selnya.Pada kenyataannya, sirkuit adder di prosesor kami dapat dibangun secara berbeda dan jauh lebih rumit. Sebagai contoh, sudah Intel 8008 45 tahun yang lalu mampu menghitung semua carry bit di muka untuk melakukan penambahan secara paralel (yang disebut adder dengan carry paralel). Siapa yang peduli, baca posting blog yang menarik tentang reverse engineering ALU Intel 8008 di blogKen Shirriff. Yaitu berbagai optimasi digunakan: misalnya, perkalian juga bermanfaat untuk tidak dilakukan "langsung".
Contoh penerapan penambah penuh pada transistor CMOS . SumberJadi kita sampai ke transistor! Meskipun, tentu saja, tidak hanya ALU bekerja pada transistor, tetapi juga unit prosesor lainnya, tetapi sebagian besar transistor digunakan dalam cache sebagai selnya.Pada kenyataannya, sirkuit adder di prosesor kami dapat dibangun secara berbeda dan jauh lebih rumit. Sebagai contoh, sudah Intel 8008 45 tahun yang lalu mampu menghitung semua carry bit di muka untuk melakukan penambahan secara paralel (yang disebut adder dengan carry paralel). Siapa yang peduli, baca posting blog yang menarik tentang reverse engineering ALU Intel 8008 di blogKen Shirriff. Yaitu berbagai optimasi digunakan: misalnya, perkalian juga bermanfaat untuk tidak dilakukan "langsung".Kesimpulan: apa yang kita pelajari?
- Ini rumit
- Jelas ditunjukkan: untuk memecahkan masalah kompleksitas yang berlebihan, insinyur menggunakan pemisahan sistem yang kompleks menjadi level (lapisan).
- Arsitektur bertingkat memberikan portabilitas: misalnya, Firefox dapat berjalan di berbagai sistem operasi dan pada perangkat keras yang berbeda.
- Interaksi antar level disebabkan oleh keterbukaan spesifikasi untuk antarmuka, layanan, dan format data, misalnya HTML dan CSS, C ++, seperangkat perintah x86, dll.
- Pahlawan kita saat ini bekerja di bagian paling bawah - sebuah transistor .
PS Saya seorang amatir (pengembang web), dan saya tahu arsitektur C ++, ASM, BT - dari kursus institut, saya bisa mengacaukan sesuatu. Silakan kirim komentar.