Cara membuat wallpaper mustahil: riwayat simetri terlarang

Di sebelah kiri adalah pola wallpaper dengan simetri rotasi urutan keenam di sekitar setiap mawar coklat-hijau. Di sebelah kanan adalah pola wallpaper dengan simetri cermin relatif terhadap garis-garis horizontal yang melewati setiap elemen elips dari ornamen jendela kaca patri.

Sekilas, menciptakan wallpaper tidak lebih sulit daripada menyelesaikan tugas dari taman kanak-kanak. Desainer dapat memilih kombinasi warna dan bentuk untuk karya asli, dan cukup gandakan menjadi dua arah. Tergantung pada pola potongan awal dan pilihan arah, simetri tambahan dapat muncul - misalnya, simetri urutan keenam pada gambar pertama, atau simetri cermin pada gambar kedua. Kedua pola diciptakan oleh ahli matematika Frank Farris dari University of California, Santa Clara.


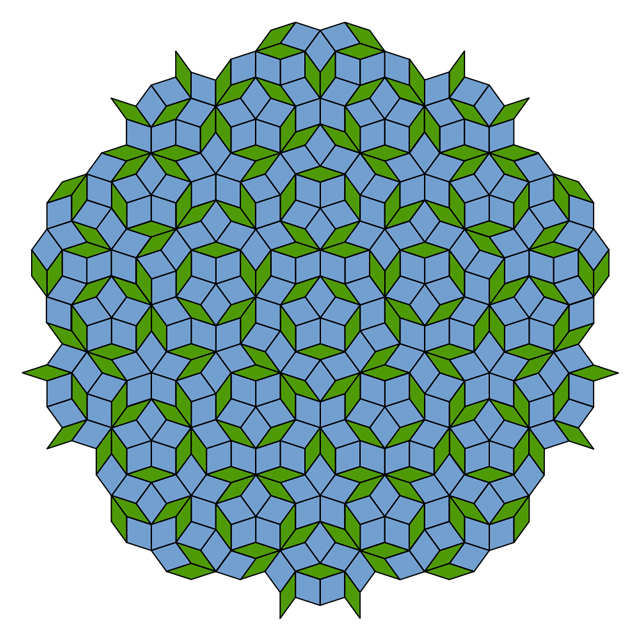Ubin Penrose menunjukkan banyak contoh simetri orde lima lokal, tetapi mereka tidak memiliki pengulangan pola. Saat mengisi area besar di pesawat, rasio jumlah ubin lebar dengan jumlah yang sempit mendekati rasio emas.

Tetapi, meskipun dimungkinkan untuk membuat wallpaper dengan simetri rotasi dari pesanan kedua, ketiga, keempat atau keenam, tidak mungkin untuk membuat wallpaper dengan simetri urutan kelima [urutan menunjukkan berapa kali pola akan menyelaraskan sendiri selama rotasi 360 ° - kira-kira. diterjemahkan.]. Pembatasan ini telah diketahui oleh ahli matematika selama hampir 200 tahun sebagai "pembatasan kristalografi". Geometri pentagon melarang pola dengan simetri orde kelima. Hal yang sama berlaku untuk pesanan tujuh atau lebih.

Namun, pola yang paling menarik, seperti ubin Penrose, menunjukkan simetri urutan kelima lokal di banyak tempat dan pada skala yang berbeda, hanya tanpa pola yang berulang. Menggunakan metode yang berbeda dari pendekatan Penrose, Farris mengekang geometri simetri orde lima yang tidak biasa dan menciptakan serangkaian gambar baru yang menarik - pseudo-wallpaper yang tampaknya tidak mematuhi, pada pandangan pertama, batasan kristalografi.


Fig. 4 Gambar

4 terlihat seperti contoh tandingan untuk batasan kristalografi, memiliki simetri rotasi orde kelima di sekitar titik A, sementara polanya dapat digeser pada pesawat dalam arah AB atau AC. Faktanya, Faris menulis dalam artikelnya untuk jurnal Notices of American Mathematical Society bahwa gambar ini hanya palsu.

"Anda tahu bahwa simetri yang Anda amati tidak mungkin," kata Stephen Kennedy dari Carleton College di Minnesota.

Simetri rotasi urutan kelima di sekitar titik A tampaknya puas. Tetapi jika Anda melihat lebih dekat, Anda akan melihat bahwa roda di sekitar titik B dan C sedikit berbeda dari A. Jika kita bisa bergerak menjauh dari pola untuk melihat lebih banyak pengulangan, maka pengulangan yang terlihat dari pola tersebut akan semakin kurang seperti pola di wilayah titik tersebut. Dan, bahkan jika salinan A yang lebih meyakinkan akan muncul di tempat lain, seperti pada Gambar. 5. Faris menunjukkan bahwa ilusi semacam itu juga dapat dibuat pada skala yang lebih besar, menjauh dari pola dan mengulanginya beberapa kali - khususnya, berapa kali sesuai dengan angka dari seri Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, ... di mana setiap angka berikut adalah jumlah dari dua sebelumnya), yang juga berperan dalam geometri ubin Penrose.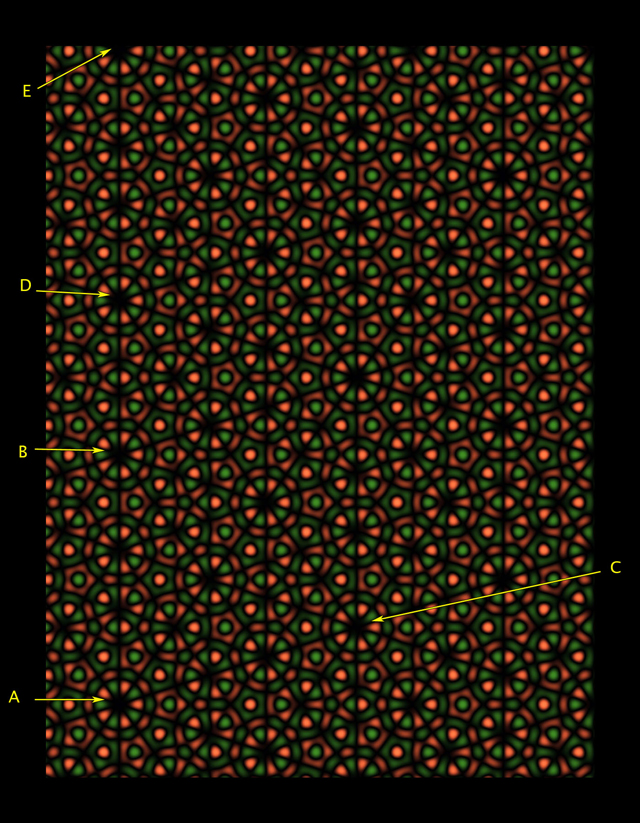


Fig. 5

"Dengan alasan, kami memahami bahwa ini semacam tipuan," kata Faris. Namun demikian, ketika dia menulis dalam artikel tersebut, gambar-gambar ini “mengundang mata kita untuk mempelajarinya dan menikmati pengulangan yang hampir sempurna.”

Faris memikirkan pemalsuan ini, mengubah teknologi yang ia buat wallpaper nyata dengan simetri rotasi urutan ke-3, seperti pada Gambar. 6.

Untuk membuat simetri urutan ke-3, Faris mulai bekerja di ruang tiga dimensi, yang memiliki satu rotasi alami, memilah-milah tiga koordinat spasial, dan titik-titik rotasi di ruang 120 derajat di sekitar diagonal. Kemudian Faris menciptakan pola wallpaper tiga dimensi, melapiskan sinusoid yang dipilih secara khusus dan menggabungkannya dengan palet warna yang telah dipilih sebelumnya. Poin bernoda tergantung pada posisi mereka pada sinusoid superimposed. Kemudian Faris mengeluarkan wallpaper datar, membatasi warna ini ke bidang dua dimensi yang tegak lurus dengan sumbu rotasi ruang asli.

Pendekatan halus dan sinusoidal untuk membuat pola wallpaper ini berbeda dari metode salin dan tempel tradisional, kata Kennedy. "Ini adalah cara yang sangat baru untuk membuat pola simetris."


Fig. 6

Prosedur yang sama yang dilakukan dalam ruang lima dimensi, tampaknya, seharusnya mengarah pada penciptaan pola dengan simetri urutan kelima - kalau saja kita tidak tahu bahwa ini tidak mungkin. Menariknya, pikir Faris, pada titik mana sistem ini gagal?

Secara teoritis, ruang lima dimensi dimungkinkan, walaupun sulit dibayangkan. Dia memiliki analog alami dari simetri rotasi orde kelima, seperti dalam ruang tiga dimensi - simetri yang ketiga. Dalam ruang lima dimensi, satu dari dua bidang dapat dipilih, yang masing-masing tegak lurus terhadap sumbu rotasi dan bidang lainnya. Masing-masing dapat diputar sekitar titik dengan 72 atau 144 derajat. Mungkin tampak sulit membayangkan dua pesawat dan garis lurus saling tegak lurus, tetapi dalam lima dimensi mereka semua memiliki ruang yang cukup.

Faris memahami masalahnya - jika bidang tegak lurus memotong ruang tiga dimensi secara akurat dan berisi wallpaper tak terbatas dengan jumlah titik tak terbatas dengan koordinat bilangan bulat, maka dua bidang tegak lurus dalam ruang lima dimensi tidak rasional, dan tidak mengandung titik dengan koordinat bilangan bulat (kecuali untuk titik referensi) . Karena pola wallpaper yang dibuat dari sinusoid diulang melalui pergeseran oleh bilangan bulat, bidang seperti itu tidak mewarisi pola dari ruang orde tinggi.

"Begitulah cara lalat muncul dalam sup," tulis Faris dalam artikel itu.

Namun demikian, ilusi struktur wallpaper muncul di dua pesawat ini, berkat partisipasi yang disebut rasio emas, angka irasional yang menggambarkan arah dua pesawat, dan angka Fibonacci.

Berkat hubungan mereka, Faris berhasil menunjukkan bahwa meskipun tidak ada titik dengan koordinat bilangan bulat di dua pesawat, masing-masing dari mereka sangat dekat dengan hamburan poin tanpa akhir dengan koordinat bilangan bulat, yang koordinatnya adalah angka Fibonacci. Setiap kali pesawat mendekati salah satu titik Fibonacci ini, polanya terlihat hampir sama dengan di titik referensi, yang menciptakan ilusi salinan yang tepat.



Faris juga menemukan cara menggabungkan warna dan pola foto alam dengan fungsi gelombang untuk memasukkannya dalam desain pola, sehingga Anda bisa mendapatkan sejumlah besar wallpaper "palsu". Pada gambar di atas, Anda dapat melihat cabang-cabang pohon yang bermigrasi dari foto tersebut.

Source: https://habr.com/ru/post/id400591/