Tautologi penting dalam sains. Bagian 1. Fisika

Apakah Anda tahu apa itu tautologi logis? Anda mungkin tahu. Dan jika Anda tidak tahu ini, penulis akan mencoba menjelaskan konsep ini sekarang. Kami tidak akan mulai beralih ke bahasa matematika yang kering dan formal, kami tidak akan menjadi pedant yang tidak berjiwa seperti Wikipedia, dan kami akan mengatakan secara kiasan: tautologi adalah sejenis Ouroboros yang menggigit ekornya sendiri. Sebagai contoh, "tidak ada yang ketika tidak ada", atau, "benda yang sempit dan cukup rendah untuk melewati pintu ini akan dengan mudah melewati itu" dan sejenisnya. Pernyataan seperti itu selalu benar, dan mereka, secara kasar, tidak membawa informasi baru. Anehnya, sejumlah hukum dan prinsip ilmu pengetahuan penting mengandung tautologi tersembunyi, yang, bagaimanapun, tidak mengurangi kepentingan dan kebenarannya. Menarik? Lalu, di bawah luka!

Kaisar Sarlac Grant Scenticus III bosan. Sangat membosankan. Biasanya, ketika dia merasa bosan, dia memainkan batu (permainan yang agak sederhana tapi rumit, mirip dengan catur, reversi, dan Go kami ). Namun, hari ini tidak ada filsuf yang biasanya bermain dengannya. Dia duduk menatap dan menatap salah satu posisi.

Eksperimen internal Grant memutuskan untuk menghitung jumlah posisi yang memungkinkan. Mari kita tinggalkan di tempat ini, dan lakukan penghitungan kita sendiri.

Menurut aturan, diizinkan untuk memiliki hingga 3 batu pada satu sel. Total ada 6 batu (3 untuk setiap pemain). Kami tidak akan mempertimbangkan jumlah semua posisi yang memungkinkan. Jauh lebih menarik untuk menghitung berapa banyak cara Anda bisa meletakkan posisi. Tapi pertama-tama, lihat gambarnya.

Untuk kesederhanaan, kami hanya mempertimbangkan satu sel. Posisi di atas dapat diperoleh, misalnya, dalam tiga cara yang berbeda di mana batu yang kami letakkan di papan: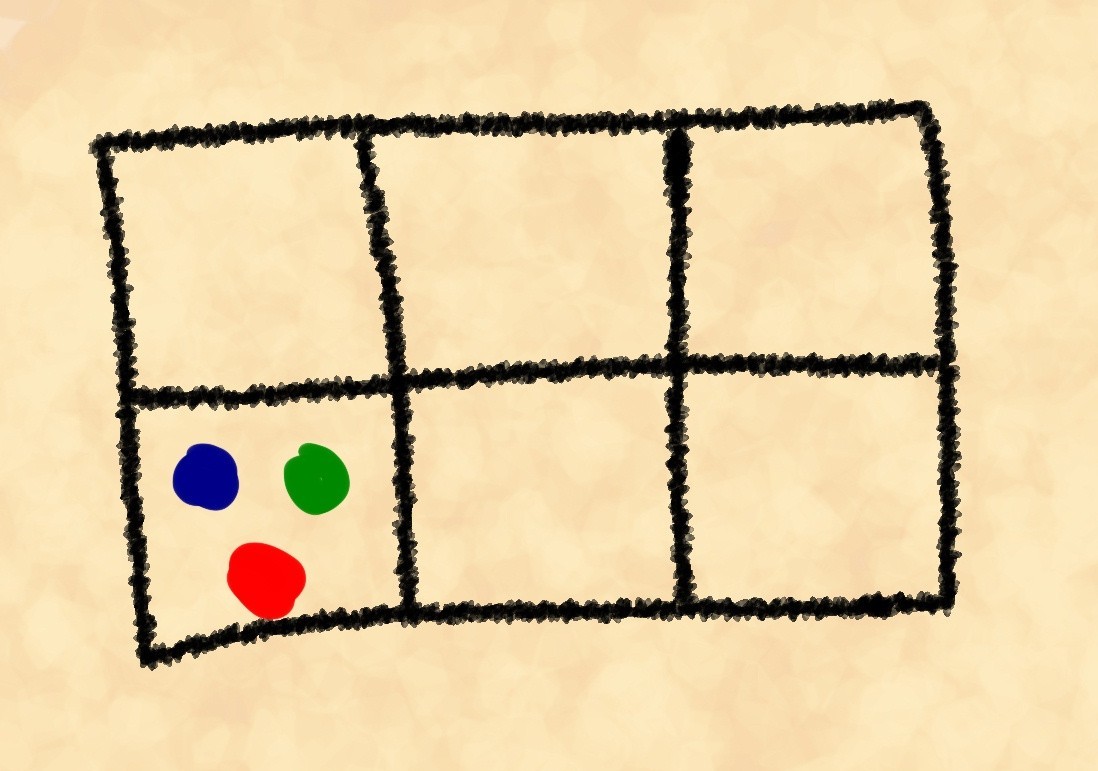

  

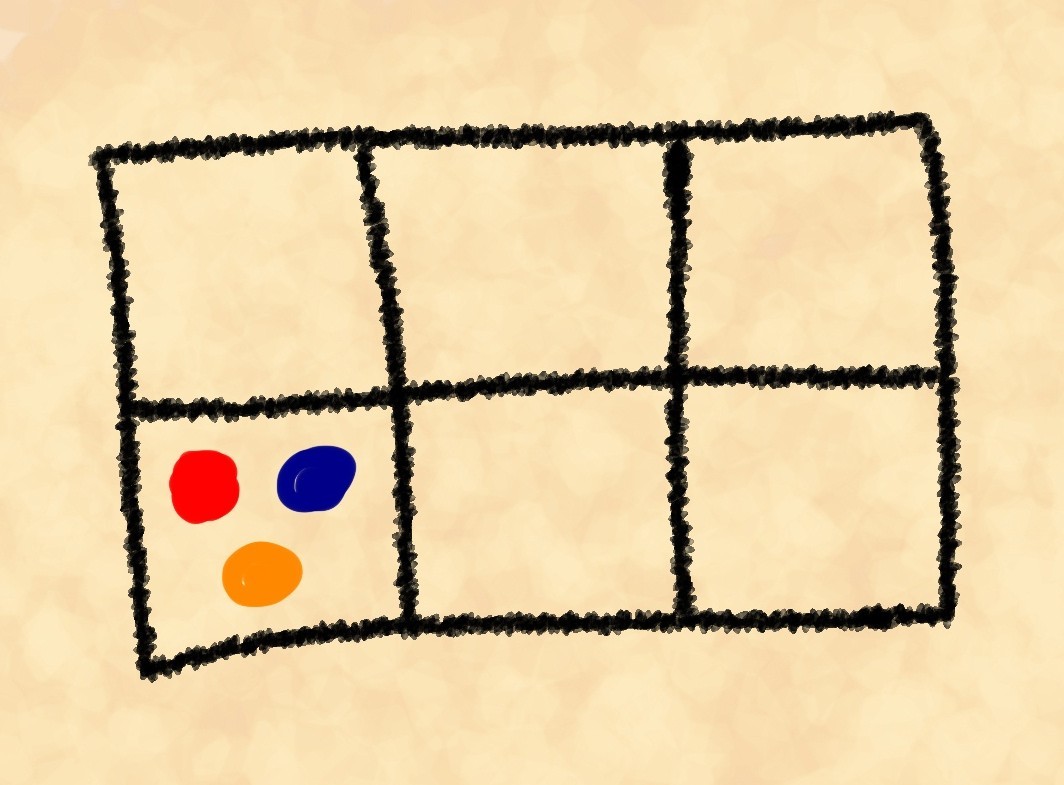Kami mengecat batu secara kondisional sehingga kami dapat membedakan satu sama lain. Jelas, ada lebih dari tiga metode. Tapi seberapa tepatnya? Yang pertama dari tiga batu bisa kita pilih dengan enam cara. Masing-masing dari enam opsi ini berlanjut dengan pilihan batu kedua dari lima yang tersisa, dan yang terakhir dari empat yang tersisa. Kita punya$$ , namun, pada saat yang sama, kami mengizinkan pengulangan, misalnya, merah-biru-kuning, kuning-merah-biru dan biru-merah-kuning adalah "perhitungan" yang sama. Untuk menemukan jumlah pengulangan, kami menemukan dalam berapa banyak cara kami dapat meletakkan tiga batu dengan warna yang sama di papan tulis. Yang pertama dapat berupa salah satu dari tiga batu yang diperlukan, yang kedua harus menjadi salah satu dari dua batu yang tersisa, yang ketiga akan menjadi batu terakhir yang kita butuhkan:$6\cdot5\cdot4=120$

$$. Sebagai hasilnya, kami memiliki 120/6 = 20 cara untuk meletakkan batu dengan cara yang diperlukan. Sebut nomor ini sebagai bobot posisi ini. Tentu saja, itu tidak ada hubungannya dengan berat fisik, hanya saja nama ini diterima secara umum dalam statistik. Mari menyulitkan tugas. Mari kita hitung bobot dari posisi-posisi ini: Jika Anda terlalu malas untuk memahami semua matematika ini, lewati paragraf berikutnya. Posisi pertama:$3\cdot2\cdot1=6$




  

1. Kami menyebarkan 2 batu di salah satu dari dua sel kiri: $$$2\cdot6\cdot5/2=30$
2. Di sel kedua kami meletakkan dua batu dari 4 sisanya: $$$4\cdot3/2=6$
3. Total yang kita miliki $$$30\cdot6/2=90$.

$$$30\cdot4\cdot3/2=180$$$. Pembagian dalam semua kasus dilakukan untuk menyingkirkan pengulangan.$4\cdot6\cdot3\cdot5\cdot2\cdot4\cdot3/24=360$

Jadi, kita memiliki bobot berikut: 90 untuk tata letak pertama, 180 untuk yang kedua dan 360 untuk yang ketiga. Pernahkah Anda memperhatikan bahwa semakin ramping posisinya, semakin sedikit beratnya? Yang Mulia Grant memperhatikan hal ini. Dan sekarang dia akan menghitung bobot untuk posisi game nyata.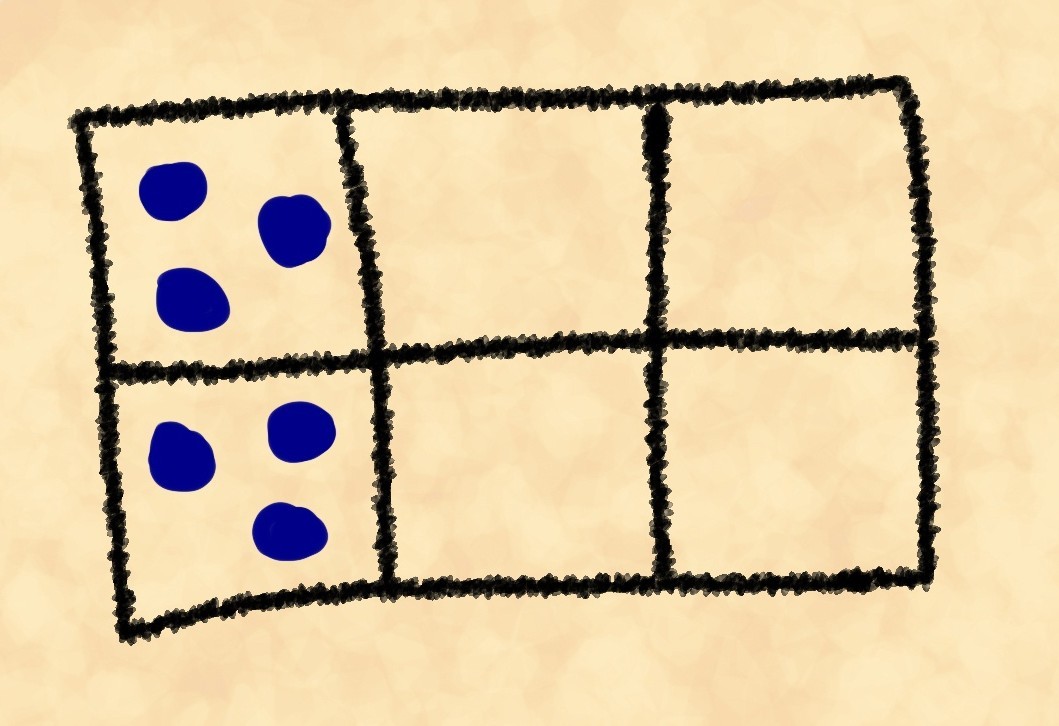

  

Dia ternyata, masing-masing, 90, 360 dan 720. Namun, di sini kesabarannya berakhir (seperti, mungkin, milikmu). Dia mendorong papan itu dengan marah, menyebarkan batu-batu secara acak, dan melihat filsuf Klofzus berdiri di pintu.

"Katakan padaku, filsuf," ia bertanya dengan nada tidak puas, "mengapa, ketika aku mendorong papan, batu-batu terbang di sekitarnya secara acak, merata, dan tidak muat tiga dalam kandang dari tepi?

Klofzius, dalam menanggapi hal ini, tersenyum dan berkata,

"Saya memperhatikan perhitungan Anda selama beberapa waktu, tuan, dan Anda mungkin sudah bisa menjawab pertanyaan ini sendiri." Tetapi saya masih akan mengatakan - batu dapat dipesan dari tepi papan dengan sembilan puluh cara berbeda, dan tujuh ratus dua puluh dapat tersebar di semua sel. Untuk batu, ada lebih banyak cara untuk tersebar di papan secara merata daripada yang dikumpulkan di tepi.

Mungkin di sini kita akan meninggalkan Sarlak. Tetapi perhatikan penjelasan Klofzus: batu-batu berserakan di papan karena ada lebih banyak cara bagi mereka untuk tersebar secara merata daripada ditata secara teratur. Dan perbedaan antara jumlah metode (bobot tata letak batu) semakin besar, semakin besar papan dan jumlah batu. Untuk papan 15 sel (3 kali 5) dan 15 batu, berat tata letak yang sepenuhnya dipesan (3 batu per sel di satu sisi) adalah sekitar 1,4 juta (1.401.400 jika tepat) dan untuk seragam (satu di setiap sel) - sekitar 1,3 kuadriliun yaitu hampir sejuta kali lipat. Karena itu, dalam hal ini jauh lebih mudah untuk mendapatkan kekacauan daripada mendapatkan pesanan. Seseorang tanpa sadar mengingat pernyataan yang begitu indah: “Telur pecah di setiap langkah, tetapi tidak ada yang pernah melihat,sehingga pecahan-pecahan telur yang pecah bersatu dan menjadi telur yang utuh. Dan semua karena hanya ada satu cara untuk mendapatkan telur utuh dan banyak cara untuk menjadi rusak. ”

Untuk meringkas keteraturan yang kami perhatikan:

Dalam proses apa pun yang terjadi dengan sendirinya, tanpa pengaruh eksternal tambahan, hasil yang dapat dicapai dalam sejumlah besar cara paling mungkin terwujud.

Lihatlah lebih dekat, ini adalah tautologi dalam segala kemuliaan. Untuk menyederhanakan banyak hal, saya hanya menegaskan bahwa "apa yang lebih mudah terjadi terjadi lebih sering." Namun, itu juga salah satu hukum fisik paling penting. Banyak dari Anda mungkin sudah mengerti bahwa kita sedang berbicara tentang hukum kedua termodinamika. Mari kita lihat salah satu formulasi "resmi" -nya:

Entropi sistem tertutup tidak dapat berkurang.

Sekarang ini kurang seperti tautologi, kan? Tapi kata pintar macam apa itu entropi?

Mari kita bayangkan udara memenuhi ruangan. Ini terdiri dari sejumlah besar molekul. Jika kita secara mental membagi ruangan menjadi sel, kita akan mendapatkan analog tiga dimensi dari permainan batu di papan yang sangat besar dengan sejumlah besar batu. Setiap posisi permainan dalam hal ini disebut macrostate sistem. Setiap tata letak batu yang menerapkan posisi tertentu adalah kondisi mikro . Kami mengambil dua angka: jumlah semua kondisi mikro yang menyadari kondisi makro ini dan jumlah semua kondisi mikro yang mungkin. Jika kita membagi yang pertama menjadi yang kedua, kita akan mendapatkan kemungkinan macrostate ini.

Definisi dari buku: entropi keadaan sistem adalah logaritma probabilitas keadaan ini.

Kami menerjemahkannya ke bahasa yang dipahami Grant - entropi suatu posisi adalah logaritma dari bobot posisi yang diberikan. Mari kita coba memperjelas ini: semakin banyak cara Anda mendapatkan posisi, semakin entropi.

Sekarang kita melihat bahwa rumusan buku dari prinsip kedua mengatakan yang berikut: dari posisi itu sendiri, hanya transisi ke posisi yang dapat diperoleh di lebih dari atau dengan jumlah jalan yang sama dengan yang awal dapat terjadi.

Mari kita coba untuk menyederhanakannya: jika kita mengguncang papan, kita akan lebih cepat mendapatkan posisi yang lebih mudah didapat.

Tampaknya kita kembali ke tautologi. Namun, bahkan jika itu adalah tautologi, prinsip kedua adalah salah satu hukum fisik yang paling penting. Selain itu, ini adalah satu-satunya hukum fisika yang memberi tahu kita bahwa waktu harus mengalir ke arah tertentu, yang membuat perbedaan antara masa lalu dan masa depan.

Akhirnya, mari kita lihat beberapa formulasi lagi dari awal kedua:

• Clausius postulat: Proses melingkar tidak mungkin, satu-satunya hasil yang merupakan perpindahan panas dari tubuh yang kurang panas ke yang lebih hangat
• Dalil Thomson: Proses melingkar tidak mungkin, satu-satunya hasil yang akan menjadi produksi pekerjaan dengan mendinginkan reservoir panas.

Seperti yang Anda lihat, tidak ada lagi tautologi. Dan tidak satu pun dari mereka yang jelas. Namun, dapat ditunjukkan bahwa kedua formulasi ini sepenuhnya sama dengan tautologis "sangat mungkin bahwa sesuatu yang lebih mungkin akan terjadi". Terkadang, untuk mempelajari sesuatu yang baru, pertama-tama kita perlu menyadari sesuatu yang jelas.

Pada bagian selanjutnya, kita akan mempertimbangkan "tautologi ilmiah" lain, yang, pada pandangan pertama, melanggar hukum kedua termodinamika.

Source: https://habr.com/ru/post/id400803/