Moon Duchin, Guru Besar Matematika dan Direktur Program Sains, Teknologi, dan Masyarakat di Tufts University (AS)

Partai-partai politik dan komisi pemilihan umum di Amerika Serikat, Rusia, dan negara-negara lain secara tradisional “menipu” dengan ukuran dan bentuk daerah pemilihan, berusaha mengisolasi bagian protes dari pemilih dalam pemesanan terpisah atau, sebaliknya, menyebarkan sedikit noda di daerah pemilihan tetangga. Karena manipulasi semacam itu - percekcokan - distrik-distrik terkadang mendapatkan garis besar yang sangat aneh. Tapi semuanya legal. Sampai sekarang, tidak ada undang-undang normal dengan rumus matematika yang menggambarkan bentuk geometris kabupaten. Associate Professor of Mathematics di Tufts University bermaksud untuk memperbaiki kekurangan ini dan menawarkan beberapa model matematika.

Jerrymandering sering digunakan di negara-negara dengan pemilihan parlemen mayoritas dan sistem partai yang kuat. Agar jumlah maksimum wakil mereka "sendiri" masuk ke parlemen, para pemilih dari partai oposisi terkonsentrasi di beberapa daerah pemilihan, sementara sisanya membuat keuntungan kecil tapi percaya diri untuk partai mereka. Itulah sebabnya konstituen dibuat dengan jumlah pemilih yang tidak sama, serta konstituen dengan bentuk teritorial yang aneh.

Sebagai contoh, di Amerika Serikat, jerigen digunakan untuk menetralisir pemilih kulit hitam sehingga kandidat mereka tidak pergi ke parlemen (ada kasus diskriminasi positif ketika itu adalah kandidat kulit hitam yang dipromosikan dengan cara ini). Dan di Rusia pada tahun 2015, sebelum pemilihan parlemen, sebuah undang - undang diadopsi pada pemotongan “kelopak” kabupaten , di mana sektor-sektor kecil kota-kota besar dengan pemilih yang tidak loyal bergabung dengan wilayah pedesaan yang luas dengan populasi yang loyal. Akibatnya, jeriken melakukan tugas yang sama - hal itu menghalangi jalannya kandidat "jahat" ke parlemen di sebagian besar distrik.

Misalnya, di wilayah Novosibirsk, otoritas membagi populasi kota menjadi empat bagian dan melampirkan masing-masing ke wilayah wilayah tersebut.


Distrik pemilihan di wilayah Novosibirsk

Di Amerika Serikat, situasi dengan percekcokan bahkan lebih buruk, karena di sebagian besar negara bagian, pemotongan distrik adalah kompetensi parlemen daerah (yaitu, pada kenyataannya, berada di tangan partai dengan mayoritas parlemen). Misalnya, Wilayah Novosibirsk bahkan tidak mendekati tingkat kebodohannya terhadap distribusi Maryland di delapan negara.


Pcs distrik kedua. Maryland


Pcs distrik ketiga. Maryland

Selain itu, konstitusi negara biasanya hanya menyediakan aturan dasar tentang bentuk konstituensi atau tidak ada aturan sama sekali. Biasanya diindikasikan bahwa distrik harus “kompak,” tetapi ini jelas pernyataan yang luas dan subyektif.

Untuk mengubah situasi, Moon Dachin membentuk sebuah organisasi ahli beranggotakan lima orang, Metric Geometry and Gerrymandering Group (MGGG), yang membuka milis untuk mulai membahas masalah persekongkolan dalam komunitas ilmiah. Dia menggambarkan tujuan organisasi dalam sebuah wawancara dengan jurnal Chronicle of Higher Education.

Apa itu kekompakan?

Associate Professor Dachin mengusulkan untuk mempertimbangkan kemungkinan menggunakan beberapa konsep untuk menggambarkan bentuk distrik yang dapat diterima, yaitu, untuk secara objektif memverifikasi persyaratan "kekompakan", yang ditulis dalam konstitusi negara.

Misalnya, Anda dapat mempertimbangkan parameter seperti skor Polsby-Popper , yang dihitung sebagai rasio area suatu wilayah dengan luas lingkaran yang panjangnya sama dengan keliling wilayah tersebut.


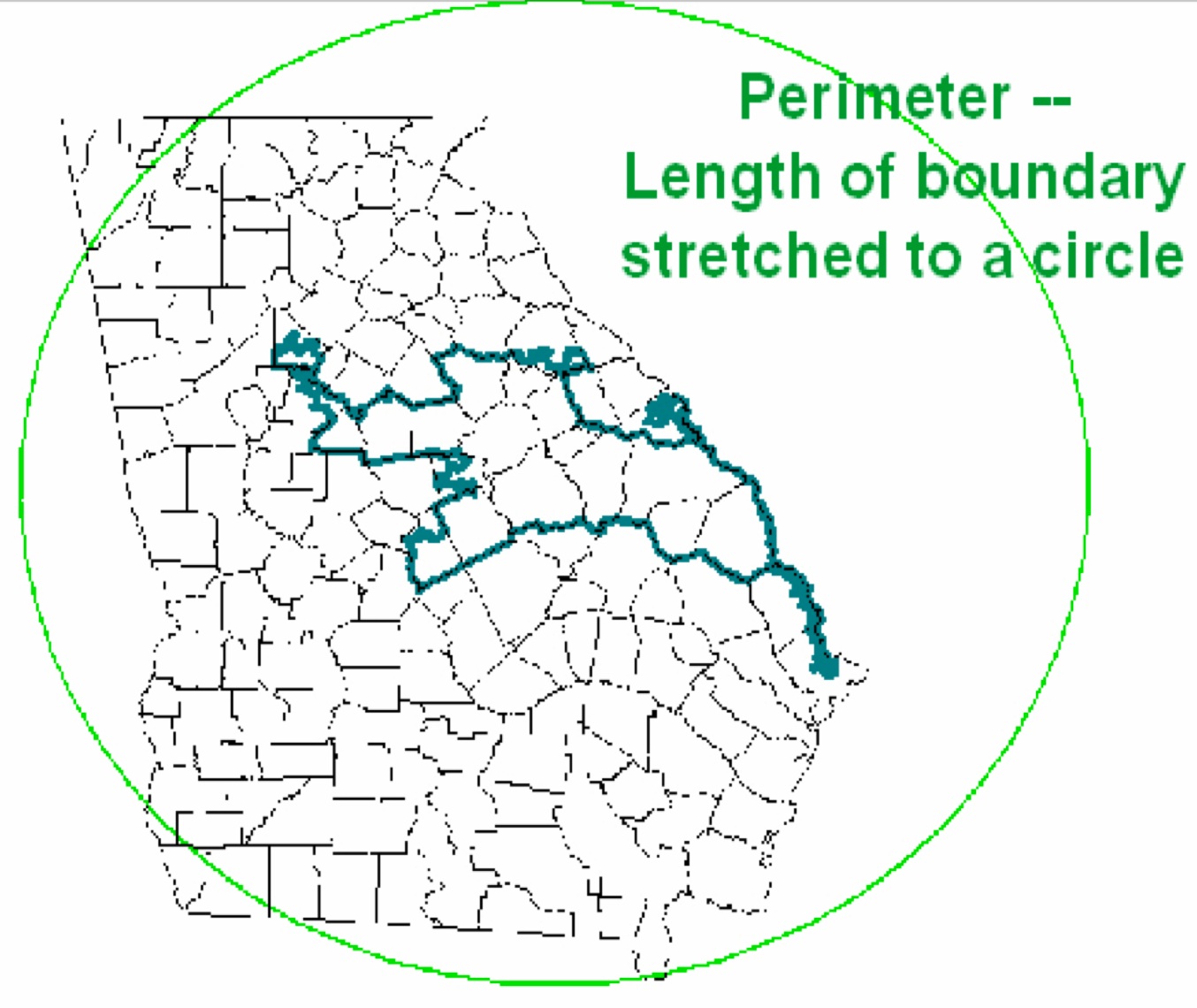Skor Popper Polsby

Pilihan lain adalah rasio sederhana dari luas kabupaten dengan luas lingkaran dalam lingkaran terbatas.


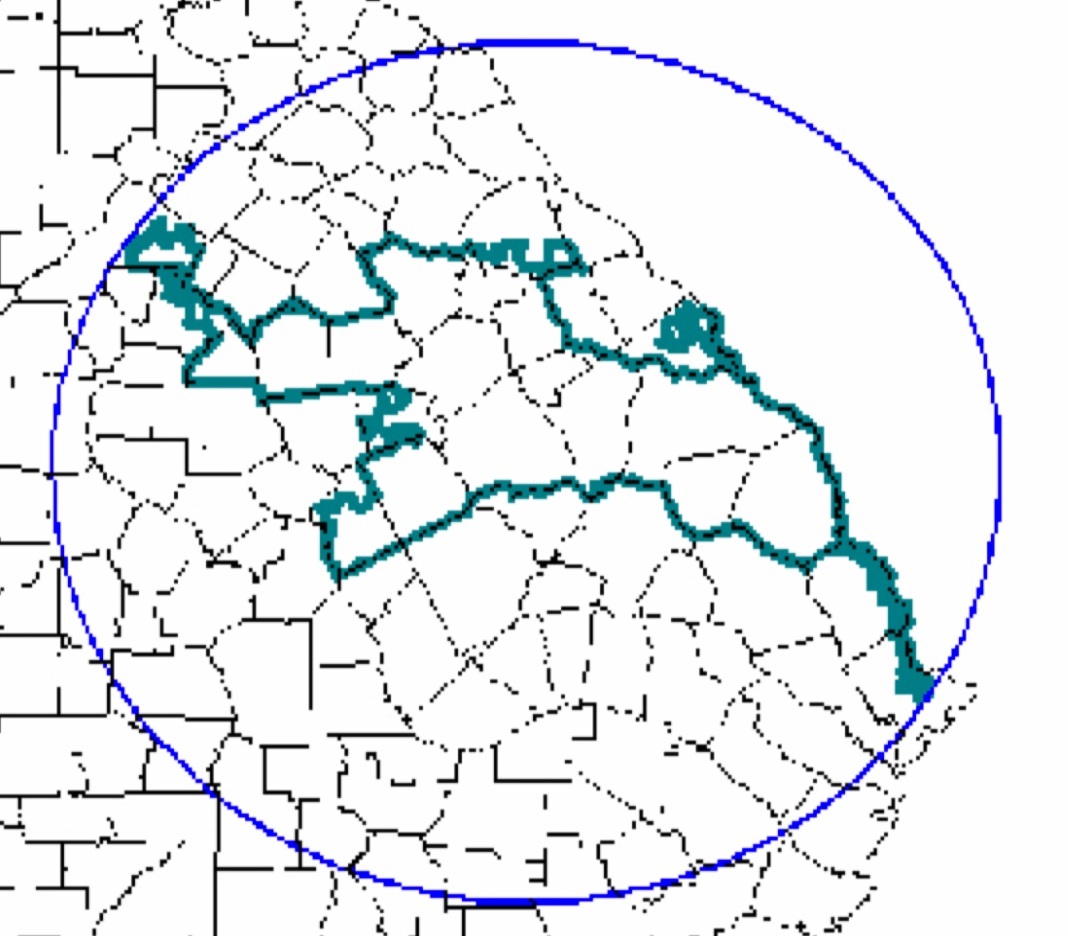Rasio luas wilayah kabupaten dengan luas lingkaran

Moon Dachin mengatakan dia saat ini sedang mengerjakan masalah geometri metrik dalam kerangka teori grup geometri . Ini adalah bidang matematika yang mempelajari kelompok-kelompok yang dihasilkan secara halus menggunakan hubungan antara sifat-sifat aljabar mereka dan sifat-sifat topologi dan geometris dari ruang-ruang di mana kelompok-kelompok semacam itu bertindak, atau dari kelompok-kelompok itu sendiri, dianggap sebagai objek-objek geometris. Di situs web pribadi Danchin , Anda dapat menemukan beberapa karya ilmiah di bidang ini di mana dia menggambarkan parameter seperti jarak rata - rata antara semua titik dari angka yang berubah-ubah (mungkin, parameter masih perlu dinormalisasi, misalnya, dengan diameter lingkaran yang dijelaskan sama). Parameter ini sangat cocok sebagai karakteristik kekompakan.

Pilihan lain untuk mengevaluasi kekompakan, yang para ahli katakan , adalah tes interokular Grofman, yang diusulkan oleh ilmuwan Amerika Bernie Grofman. Tes ini memungkinkan Anda untuk menentukan secara visual tingkat kesulitan dengan mengukur seberapa lebar mata seseorang, siapa yang melihat peta dan mengevaluasi skala penipuan. Ngomong-ngomong, tes yang sama pernah ditawarkan untuk mengevaluasi porno "hardcore". Intinya adalah sulit untuk memformalkan hal-hal seperti itu, tetapi ketika Anda melihatnya, Anda segera mengerti (lihat lagi di kabupaten di Maryland).

Associate Professor di Tufts University yakin bahwa dengan bantuan matematika, banyak masalah sosial dapat diselesaikan. Tetapi kesulitannya adalah bahwa politisi sering tidak dapat memahami konsep matematika sederhana. Oleh karena itu, akan sangat sulit untuk meyakinkan mereka untuk memasukkan formula tersebut ke dalam undang-undang dan Konstitusi negara. Bagaimanapun, mereka harus dipahami terlebih dahulu. Moon Dachin memberikan contoh konsep kurangnya efisiensi , yang menggambarkan Jerrymandering dengan contoh sederhana - kasus unik ketika seorang hakim AS memahami matematika dan mengatakan bahwa ia "menyukainya". Dokumen matematika ini membentuk dasar dari Whitford v. Nichol di Wisconsin. Ini adalah bagaimana konsep matematika harus dijelaskan dan disajikan kepada hakim, politisi dan masyarakat: sejelas dan meyakinkan mungkin.