Intro

Pos ini ditulis di bawah kesan pos luar biasa dari Habr ini, di mana penulis secara visual, menggunakan model dua dimensi yang digambar programnya, menjelaskan cara kerja Teori Relativitas Khusus.

Saya bekerja di bidang TI, dan melalui pendidikan - seorang ahli fisika teoretis. Sudah lama saya gemar mempopulerkan sains, dan khususnya teori fisika. Saya akan mencoba, mirip dengan posting di atas pada teori relativitas khusus, untuk menjelaskan dengan contoh yang disiapkan khusus bagaimana mekanika kuantum bekerja.

Model yang saya pertimbangkan sama sekali tidak baru. Lebih dari enam bulan lalu, Chris Cantwell memposting pengumuman di papan permainan baru: catur kuantum di YouTube (banyak orang mungkin tahu tentang ini dari video viral ini ).

Baru-baru ini, game ini dirilis di Steam, harganya 249 rubel. Ada implementasi lain - aplikasi gratis untuk iOS (saya tidak tahu apakah itu ada di Google Play). Namun, dalam proses bermain game dengan teman-teman, saya secara eksperimen menemukan bahwa itu tidak tepat dari sudut pandang mekanika kuantum. Implementasi seperti itu dapat disebut catur statistik daripada catur kuantum.

Jadi saya memutuskan untuk menulis implementasi saya, dengan seluk-beluk dan superposisi. Dalam implementasi saya, saya mencoba untuk memperbaiki kekurangan-kekurangan yang, menurut pendapat saya, hadir dalam versi Steam (misalnya, pion saya juga bisa bergerak dengan gerakan kuantum, seperti semua bagian lainnya). Semuanya jelas tentang aplikasi iOS: setiap implementasi catur kuantum harus benar-benar kuantum, mis. tidak hanya untuk probabilistik, tetapi untuk mendukung efek mekanika kuantum seperti gangguan, keterikatan, dll.

Versi alpha di-host di http://truly-quantum-chess.sloppy.zone . Di sana Anda dapat bermain dengan diri sendiri, "bermain" untuk dua pemain secara bergantian; Atau mainkan permainan penuh dengan seorang teman. Gameplay berlangsung langsung di browser, Anda tidak perlu mengunduh dan menginstal apa pun.

Penafian: Saya tidak mengklaim sebagai deskripsi lengkap tentang hukum fisika kuantum. Tetapi dalam posting tidak akan ada formula tunggal: hanya gambar, hanya hardcore.

Superposisi

Jadi, sama saja, tentang apa catur kuantum ini? Perbedaan utama mereka dari catur konvensional adalah bahwa permainan ini dimainkan di superposisi papan catur . Secara sederhana - di beberapa papan pada saat yang sama.

Itu terlihat seperti ini:

Gadai biru dalam posisi super: menempati posisi c2 dan c4 pada saat yang sama .
Hal yang sama berlaku untuk kuda merah: ia berada di posisi superposisi g8 dan e3 .

Apa maksudnya ini?

Pembaca, yang sedang menunggu klarifikasi tentang arti sebenarnya dari superposisi, saya harus mengecewakan: tidak ada penjelasan.

Superposisi hanyalah superposisi. Mereka benar-benar ada di alam. Kita hampir tidak mengamatinya dalam kehidupan sehari-hari karena dekoherensi - interaksi dengan lingkungan yang kacau, akibatnya superposisi dengan cepat runtuh.

Namun, tidak ada yang secara fundamental mencegah kita menyediakan kondisi di mana superposisi akan tetap untuk waktu yang lama. Inilah tugas yang dihadapi, misalnya, insinyur yang mengerjakan komputer kuantum.

Kemungkinan

Ada interpretasi lain tentang superposisi. Kita dapat mengatakan bahwa pion biru tidak pada dua kotak c2 dan c4 pada saat yang sama, tetapi pada salah satu kotak ini. Kami tidak tahu yang mana. Selain itu, kemungkinan berada pada masing-masing sel adalah 50% (seperti yang ditunjukkan oleh strip horizontal yang membagi masing-masing setengah dari pion menjadi setengah).

Ternyata itu dalam kenyataan

• Interpretasi pertama (gadai pada e2 dan e4 pada saat yang sama) lebih akurat ketika sistem tidak berinteraksi dengan alat pengukur. Tentang apa yang harus dipertimbangkan sebagai alat pengukur pada papan catur, kita akan melangkah lebih jauh pada bagian tentang keruntuhan.
• Interpretasi kedua (bidak pada e2 atau e4 , kami tidak tahu di mana) lebih akurat pada saat berinteraksi dengan lingkungan, misalnya, dengan alat pengukur.

Meskipun tidak ada interaksi, kedua opsi (gadai pada e2 dan pada e4 ) ada sendiri. Gim ini dimainkan dengan superposisi opsi. Ini adalah proses kompleks yang secara alami mencampurkan kedua opsi, memaksa mereka untuk saling mempengaruhi. Karena itu, tidak dapat dikatakan bahwa hanya ada satu pilihan.

Ketika interaksi diaktifkan, interpretasi probabilistik benar. Probabilitas menemukan pion pada e2 dalam kasus ini adalah 50%. Mesin catur kuantum, tentu saja, menyelesaikan situasi seperti itu dengan memilih opsi menggunakan generator angka acak.

Bagaimana cara membuat superposisi?

Satu perubahan penting ditambahkan ke aturan catur biasa: untuk setiap gerakan pemain dapat membuat gerakan catur biasa atau yang disebut langkah kuantum.

• Langkah normal hanyalah langkah dengan bidak catur, menurut aturan catur biasa. Jika permainan saat ini sedang dimainkan di superposisi, maka langkah tersebut dilakukan pada semua papan superposisi, di mana ia diizinkan sesuai dengan aturan catur . Omong-omong, ini jauh dari sepele seperti yang terlihat. Misalnya, jika pion berada di superposisi di jalur rook, maka langkah seperti itu hanya mungkin jika tidak ada pion (karena, menurut aturan, rook tidak dapat melompati potongan). Oleh karena itu, setelah langkah biasa seperti itu, benteng itu sendiri akan berada di superposisi: di papan di mana tidak ada bidak, dia membuat langkah; dan di papan di mana gadai berada di jalan, langkah itu dilarang, sehingga benteng tetap di tempatnya.

  
  

• Langkah kuantum adalah gerakan di mana Anda dapat memasukkan papan catur ke superposisi. Sebuah gerakan kuantum terdiri dari dua gerakan biasa dalam satu baris oleh potongan yang sama. Kedua gerakan harus benar dari sudut pandang catur biasa (lebih tepat, gerakan diterapkan di papan dari superposisi jika kedua gerakan itu benar dari sudut pandang catur reguler di papan ini). Semacam "pembayaran" untuk kesempatan untuk pergi dua kali berturut-turut adalah bahwa setelah perpindahan kuantum angka tersebut bergerak ke superposisi : secara bersamaan ia membuat dua gerakan dan tetap di tempatnya. Selanjutnya, ketika interaksi terjadi (lihat di bawah tentang "runtuh"), menggunakan generator nomor acak itu akan memutuskan mana dari dua bagian superposisi yang ada dan yang tidak. Tetapi sementara kedua bagian ada secara bersamaan.

  
  

Untuk melakukan gerakan normal, Anda perlu mengklik gambar (disorot dengan warna hijau), dan kemudian pada sel yang ingin Anda tuju. Untuk membuat gerakan kuantum, Anda perlu mengklik dua kali pada gambar (disorot dengan warna ungu), lalu klik sekali pada sel perantara (disorot dalam warna hijau), dan kemudian pada yang terakhir.

Selain itu, aturan diizinkan untuk membuat gerakan kuantum tunggal, yaitu kuantum bergerak, di mana gambar tidak membuat dua bergerak berturut-turut, tetapi satu.

Batasan penting: menurut aturan, Anda tidak bisa memakan sosok musuh dalam gerakan kuantum. Kesempatan seperti itu membuat game terlalu tak terduga. Langkah kuantum hanya bisa dilakukan pada sel kosong.

Mati dan hidup

Kasus khusus superposisi kepentingan tertentu adalah superposisi di mana sosok itu hidup dan mati. Ambil contoh papan catur kuantum dari contoh di atas. Setelah bidak biru f2: e3 bergerak, The Reds kehilangan setengah dari ksatria mereka ...

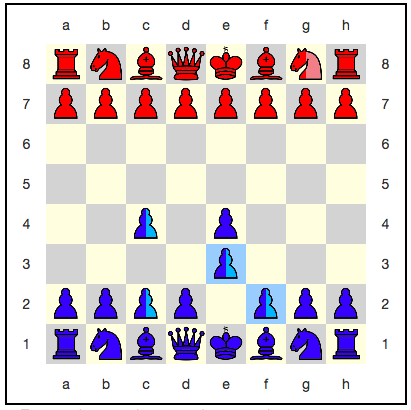
Pertama, bidak biru itu sendiri berada di posisi super. Ini karena pion berjalan dan makan dengan cara yang berbeda. Di papan di mana ksatria merah berada di e3 , pion berhasil memakannya dan beralih ke e3 . Di papan di mana ksatria tidak ada di sana, pion tidak bisa bergerak seperti itu, karena dia tidak punya apa-apa untuk dimakan. Karena itu, ia tetap menggunakan f2 .

Kuda merah itu ternyata hidup dan mati. Suatu saat di masa depan, ketika akan ada interaksi dengan alat pengukur (untuk lebih lanjut tentang ini, lihat bagian "runtuh" ​​di bawah), situasi ini akan diselesaikan menggunakan generator nomor acak. Entah karena The Reds punya kuda, atau ternyata dia tidak. Probabilitas hasil adalah 50%.

Patut dicatat bahwa sampai situasinya teratasi dan kuda berada di posisi super, The Reds dapat terus bermain dengan setengah dari kudanya. Benar, dengan probabilitas 50% ternyata setiap gerakan oleh setengah ksatria ini hanyalah kehilangan belokan.

Skakmat

Cek dan tikar sangat sulit diimplementasikan, karena tidak jelas apa yang harus dilakukan dalam situasi di mana raja berada dalam superposisi cek dan bukan cek; jodoh dan bukan jodoh. Oleh karena itu, aturan catur biasa disederhanakan: tidak ada catur atau skakmat; untuk memenangkan catur kuantum Anda harus makan raja musuh.

Patut dicatat bahwa raja, seperti tokoh lainnya, dapat berada di posisi yang sangat tinggi. Jika Anda makan setengah raja, maka kemenangan dijamin dengan probabilitas 50%. Namun, permainan terus berlanjut dalam kasus ini! Jika, katakanlah, rajamu dimakan setelah ini, maka ini tidak berarti Anda kalah. Lagipula, rajamu dimakan hanya di papan superposisi di mana Anda belum menang! Yaitu nomor acak akan dihasilkan dan Anda akan kalah / menang dengan probabilitas 50%.

Ini adalah salah satu contoh manifestasi dari "interaksi dengan alat pengukur" yang menghancurkan superposisi pada papan catur kuantum.

Tombol Capitulate juga jauh dari sesederhana kelihatannya. Menyerah hanya terjadi di papan itu dari superposisi di mana permainan masih berlangsung. Yaitu jika Anda berada di superposisi di mana Anda telah menang dengan probabilitas 75% (mis. musuh memiliki 25% raja) dan Anda mengklik Kapitulasi , maka Anda kalah dengan probabilitas 25%. Dan dengan probabilitas 3/4 Anda menang dengan menyerah! Lebih lanjut tentang ini di bagian selanjutnya:

Keabadian kuantum dan perlindungan terhadapnya

Tombol Capitulate dapat berguna untuk melindungi dari strategi permainan berdasarkan apa yang disebut. keabadian kuantum . Mari kita bahas ini lebih detail.

Pertimbangkan posisi catur ini:

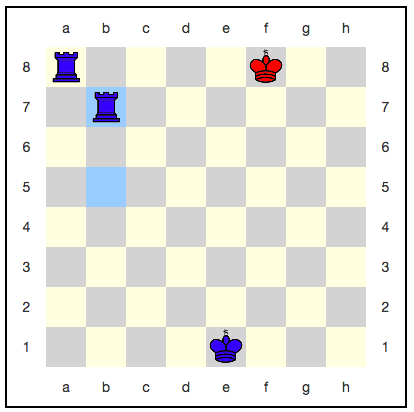
Dalam catur reguler, ini adalah skakmat klasik dengan dua benteng. Tetapi dalam catur kuantum tidak ada tikar, sebagai gantinya Anda harus makan raja.

Tampaknya di sini raja tidak punya tempat untuk mundur: langkah selanjutnya pasti akan memakannya. Namun, ada strategi menggunakan keabadian kuantum: merah dapat menghancurkan raja mereka dengan setiap gerakan, dan dia tidak akan pernah dimakan sepenuhnya. Misalnya, berikut adalah urutan gerakan:

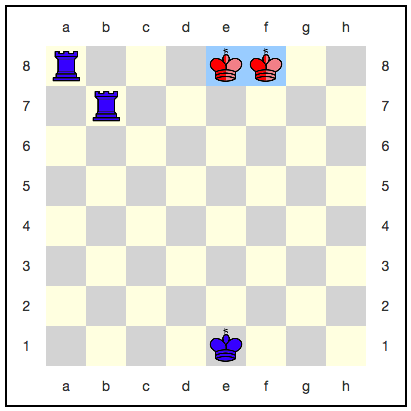
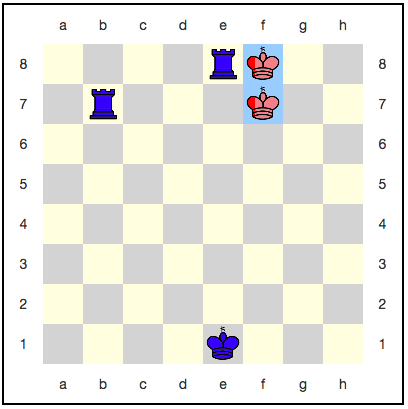
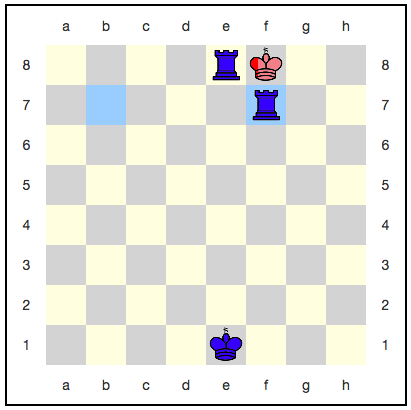
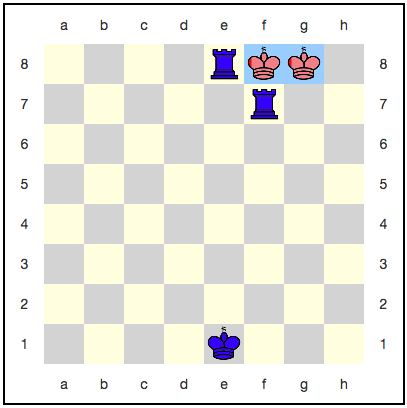
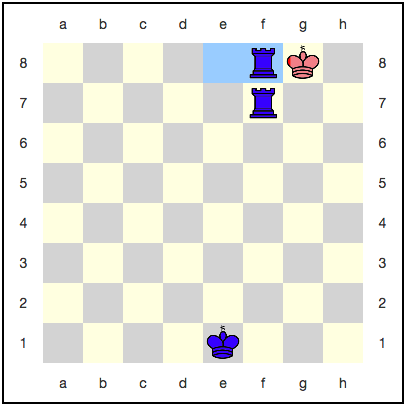
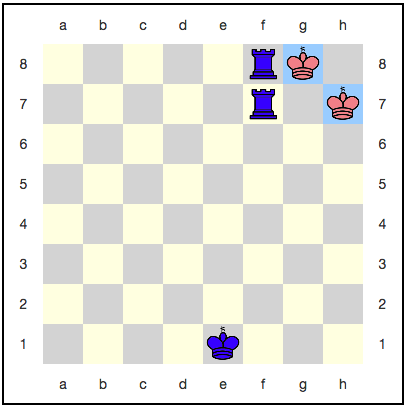
Dengan setiap gerakan, probabilitas memenangkan biru meningkat, tetapi itu tidak akan pernah mencapai satu. Ternyata permainan akan berlangsung selamanya, dan warna biru tidak akan mendapatkan kemenangan yang layak?

Dalam situasi seperti itu, anehnya, penyerahan berguna. Jika probabilitas kemenangan biru sama, katakanlah, 65535/65536, maka Anda dapat dengan aman mengklik menyerah. Seperti dijelaskan di atas, penyerahan hanya akan terjadi pada papan-papan dari superposisi di mana permainan masih berlangsung. Yaitu kemenangan biru dengan probabilitas 65535/65536, cukup menyerah!

Nah, jika berhasil 1/65536 ... Mungkin ini sangat tidak menyenangkan :)

Perkecil: "interaksi dengan perangkat pengukur" yang sama "

Dalam catur kuantum, superposisi sewenang-wenang potongan diperbolehkan. Selain itu, menciptakan superposisi tidak hanya menyenangkan: menjadi pemula dalam catur biasa dan bermain melawan seorang grandmaster, Anda dapat sangat memperlancar keunggulannya di depan Anda dengan memperkenalkan papan ke dalam superposisi kompleks!

Namun, ada superposisi yang dianggap terlalu gila. Superposisi semacam itu tidak bisa ada; begitu mereka muncul, mesin catur kuantum memulai mekanisme penghancuran superposisi seperti itu, atau "interaksi dengan alat pengukur" yang sama.

Kriteria sederhana: tidak ada superposisi di mana sel yang sama ditempati oleh dua atau lebih angka pada saat yang sama. Setuju, itu akan terlalu membingungkan dan sulit jika Anda dapat memiliki kuda dan benteng musuh di alun-alun yang sama pada saat yang sama?

Superposisi angka vs superposisi papan

Dari catatan khusus adalah proses mogok superposisi. Kami adalah superposisi apa pun (demi mereka, game ini dibuat), oleh karena itu, dengan kehancuran kami ingin menyimpan superposisi sebanyak mungkin. Sebagai contoh, pertimbangkan situasi ini:

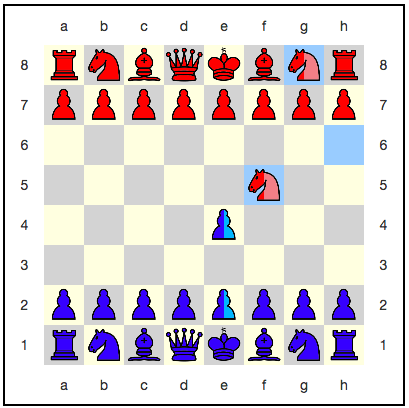
Apa yang terjadi ketika pion biru mengambil ksatria merah e4: f5 ?

Salah satu kesalahan logis umum yang dapat dibuat dalam mekanika kuantum adalah pemahaman umum yang tidak memadai tentang superposisi. Jika, misalnya, Anda berdebat dari sudut pandang tokoh-tokoh individu - katakanlah, ini adalah bidak, itu adalah superposisi - sangat mudah untuk mengarahkan diri Anda ke jalan buntu.

Untuk mencegah hal ini terjadi, cara yang paling pasti adalah dengan mengingat bahwa seluruh sistem selalu dalam superposisi, mis. dalam kasus kami, papan catur. Tidak mengherankan bahwa mesin catur kuantum bekerja berdasarkan prinsip ini. Pertimbangkan situasi di atas dalam tampilan mesin:

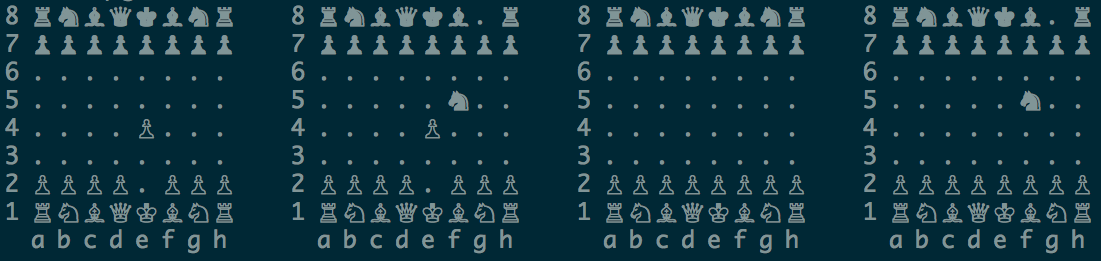
Dapat dilihat bahwa mesin mewakili superposisi persis dalam bentuk yang disebutkan di atas: sebagai satu set papan. Dalam hal ini, 4 papan yang ditunjukkan di atas dimungkinkan, karena ksatria merah dan bidak biru bisa bergerak atau tidak. Papan catur kuantum adalah superposisi dari empat papan biasa.

Representasi ini lebih akurat, dan memberi pengguna informasi lengkap tentang keadaan kuantum papan catur. Berbeda dengan representasi di antarmuka yang hanya menunjukkan probabilitas semua angka. Seperti yang direncanakan, pemain itu sendiri harus tetap dalam keadaan kuantum berdasarkan gerakan sebelumnya. Kemampuan untuk berpikir dalam hal mekanika kuantum dengan cara ini adalah kartu truf yang kuat di tangan pemain dalam catur kuantum.

Runtuh minimal

Pada superposisi papan jelas terlihat bahwa setelah pindah e4: f5 :

1. Di papan pertama: gadai tidak bisa berjalan secara diagonal, karena dia tidak punya apa-apa untuk dimakan. Tidak ada yang akan berubah, sel f5 kosong.
2. Di papan kedua: gadai akan bisa makan ksatria. Ada pion di sel f5 .
3. Di papan ketiga: sama sekali tidak ada pion di e4 . Langkah itu gagal, sel f5 kosong.
4. Di papan keempat: tidak ada lagi pion di e4 . Langkah itu gagal, kuda itu tetap di f5 .

Setelah menerapkan langkah, konflik muncul antara ksatria dan bidak atas sel f5 . Di papan kedua sekarang ada bidak, dan pada keempat - seorang ksatria.

Seperti yang telah kita bahas, kami ingin menyelesaikan konflik ini, sambil menghancurkan superposisi sesedikit mungkin. Oleh karena itu:

• Papan pertama dan ketiga tidak bertentangan dengan siapa pun. Karena itu, keruntuhan seharusnya tidak mempengaruhi mereka. Mereka akan tetap, dan permainan akan berlanjut pada mereka.
• Dewan kedua dan keempat saling bertentangan. Oleh karena itu, di antara mereka, menggunakan generator angka acak, opsi yang bertahan dipilih, dengan probabilitas 50/50.

Opsi pertama: kuda itu selamat

Papan kedua dibuang, dan permainan berlanjut pada superposisi papan dengan angka 1, 3, 4:

Perhatikan bahwa probabilitas pion posterior didistribusikan kembali! Sekarang, dengan probabilitas 2/3, pion ada di e2 (papan 3 dan 4), dan dengan probabilitas 1/3 itu ada di e4 (papan 1).

Ini benar! A priori, pion berada di e2 dengan probabilitas 50%, tetapi probabilitas ini berubah setelah nomor acak dihasilkan . Probabilitas posterior adalah 66,7%.

Hal yang sama berlaku untuk kuda (pembaca dapat menghitung papan dan memastikan bahwa kemungkinan menemukan kuda di f5 telah berubah dari 50% menjadi 33,3%).

Beginilah hasilnya terlihat di antarmuka:

Pilihan kedua: kuda itu dimakan

Papan keempat dibuang, dan permainan berlanjut pada superposisi papan dengan angka 1, 2, 3:

Dalam hal ini, kuda sekarang berada di posisi yang sangat tinggi antara yang hidup dan yang mati, seperti kucing Schrödinger. Dan pion dengan probabilitas 33,3% tersebar di posisi e2 , e4 , f5 . Beginilah hasilnya terlihat di antarmuka:

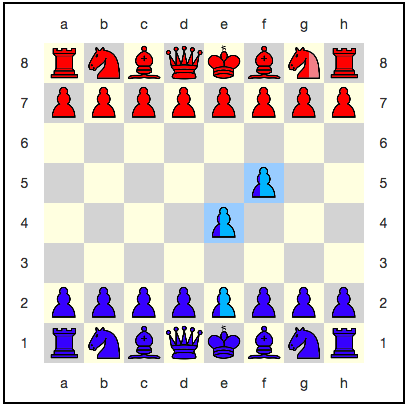
Keterikatan kuantum

Salah satu fenomena paling terkenal dan menarik di dunia kuantum adalah keterikatan kuantum. Ini pertama kali dipertimbangkan oleh Einstein dalam eksperimen pemikiran yang disebut paradoks EPR :

Pertimbangkan pasangan partikel-antipartikel yang terbentuk selama peluruhan partikel diam yang lebih berat (mis. Istirahat), misalnya, sebuah meson. Einstein berpendapat bahwa menurut hukum kekekalan momentum, momentum suatu partikel dan antipartikel dihubungkan oleh hukum kekekalan momentum; yang berarti bahwa dengan mengukur koordinat partikel dan momentum antipartikel, seseorang dapat menghitung momentum partikel menggunakan hukum ini, dan oleh karena itu dengan mengukur momentum partikel dan antipartikel, mis. melanggar prinsip ketidakpastian Heisenberg. Apakah ini berarti bahwa "deskripsi realitas mekanis-kuantum tidak lengkap" ©?

Bohr mengusulkan solusi untuk paradoks ini: setelah mengukur momentum suatu partikel, momentum antipartikel langsung mengubah nilainya , yang berarti koordinatnya tidak terdefinisi. Demikian pula, setelah mengukur koordinat antipartikel, koordinat partikel langsung mengubah nilainya , yang berarti bahwa momentumnya tidak pasti.

Apa sifat dari "jangka panjang mimpi buruk" ini?

Sekarang dapat dipercaya bahwa penjelasan Bohr benar. Ternyata jauh lebih logis dan dapat dipahami jika kita menerjemahkannya ke bahasa yang benar: kita harus membuat pernyataan tentang superposisi sistem partikel + antipartikel , dan bukan tentang superposisi komponen individualnya.

Pertimbangkan situasi ini dalam contoh yang jauh lebih ilustratif: di papan catur kuantum.

Keterikatan dalam catur kuantum

Papan catur kuantum memungkinkan Anda untuk merasakan konsep keterikatan catur. Untuk menerjemahkan papan ke dalam keadaan keterjeratan catur, Anda harus ... melewati satu bagian melalui bagian lainnya. Pertimbangkan sebuah contoh:

The blue go the queen (ratu) d1: f3 . Ini adalah langkah biasa, non-kuantum! Tapi itu tidak mungkin di semua papan superposisi. Mari kita lihat bagaimana situasinya dalam presentasi mesin catur kuantum:

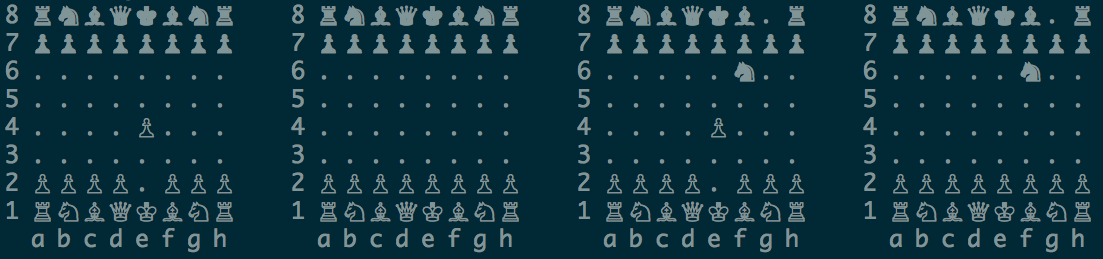
Suatu gerakan dimungkinkan pada papan 1 dan 3, yaitu pada dua dari empat papan. Karena itu, dalam hal ini, gerakan non-kuantum yang biasa akan memperkenalkan ratu biru ke dalam superposisi:

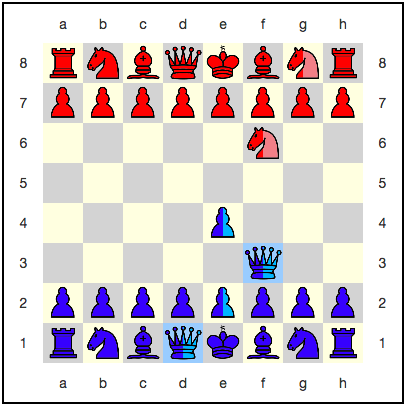
Namun, ada sesuatu yang tidak segera terlihat. Mari kita lihat tampilan engine:

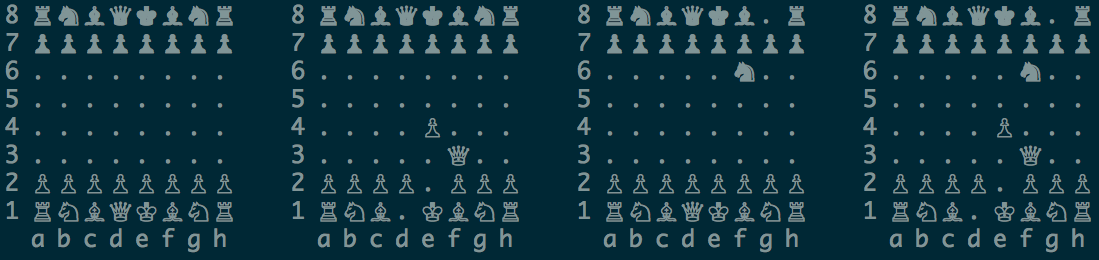
Pernyataan: ratu tersebar di posisi d1 dan f3 dengan probabilitas 50%; e2 e4 50%, : e2 , – d1 ; e4 – f3 .

, -. !

, f6:e4 . e4 , . :

, (66.7% e2 33.3% ) .

:

" " -. ; ( – ) , . , . , ( ), .

, – , ; , .. – , .

, . , . , , . , .. .

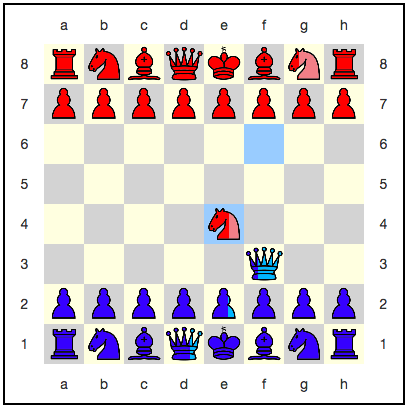
, , e4 f3 25%, , 50%, .

Kesimpulan

. , .

:

1. – ,
2. -

, ; , . , – .

!