Karakteristik aliran linier dari turbin uap. Bagian 2. Contoh konstruksi untuk turbin PT-80 di MATLAB

Kata pengantar untuk bagian pertama

Memodelkan turbin uap adalah tugas harian bagi ratusan orang di negara kita. Alih-alih model kata , itu adalah kebiasaan untuk mengatakan karakteristik pengeluaran . Karakteristik konsumsi turbin uap digunakan dalam menyelesaikan masalah seperti perhitungan konsumsi spesifik bahan bakar setara untuk listrik dan panas yang dihasilkan oleh pembangkit listrik tenaga termal; optimalisasi CHP; perencanaan dan pemeliharaan mode pembangkit listrik termal.

Saya telah mengembangkan karakteristik aliran baru turbin uap - karakteristik aliran linier dari turbin uap. Karakteristik aliran yang dikembangkan nyaman dan efektif dalam menyelesaikan masalah ini. Namun, saat ini hanya dijelaskan dalam dua makalah ilmiah:

1. Optimalisasi pengoperasian pembangkit listrik termal dalam kondisi pasar grosir tenaga listrik dan kapasitas Rusia ;
2. Metode komputasi untuk menentukan konsumsi spesifik bahan bakar ekivalen dari pembangkit listrik termal untuk energi listrik dan termal yang dipasok dalam mode generasi gabungan .

Dan sekarang di blog saya, saya ingin:

• pertama, dalam bahasa yang sederhana dan dapat diakses untuk menjawab pertanyaan dasar tentang karakteristik laju aliran baru (lihat. Karakteristik laju aliran linier dari turbin uap. Bagian 1. Pertanyaan dasar );
• kedua, berikan contoh membangun karakteristik aliran baru yang akan membantu memahami metode konstruksi dan sifat-sifat karakteristik tersebut (lihat di bawah);
  
• ketiga, untuk menyangkal dua pernyataan terkenal mengenai mode operasi turbin uap (lihat. Karakteristik aliran turbin uap yang linier. Bagian 3. Menghilangkan mitos tentang pengoperasian turbin uap ).
  

1. Sumber data

Data awal untuk membangun karakteristik aliran linier dapat

1. nilai daya aktual Q ₀ , N, Q _p , _Qt diukur selama pengoperasian turbin uap,
2. nomograms qt gross dari dokumentasi normatif dan teknis.

Tentu saja, nilai sesaat aktual Q0, N, _Qp , _Qt adalah data sumber yang ideal. Mengumpulkan data semacam itu menghabiskan waktu.

Dalam kasus di mana nilai aktual Q ₀ , N, Q _p , Q _t tidak tersedia, Anda dapat memproses nomograms q _t gross. Mereka, pada gilirannya, diperoleh berdasarkan pengukuran. Baca lebih lanjut tentang tes turbin di VM Gornstein dan Metode lain untuk mengoptimalkan mode sistem energi .

2. Algoritma untuk membangun karakteristik aliran linierisasi

Algoritma konstruksi terdiri dari tiga langkah.

1. Terjemahan nomogram atau hasil pengukuran menjadi tampilan tabular.
2. Linierisasi karakteristik aliran turbin uap.
3. Penentuan batas rentang kendali turbin uap.

Ketika bekerja dengan nomograms qt gross, langkah pertama adalah cepat. Karya ini disebut digitalisasi . Mendigitalkan 9 nomogram untuk contoh saat ini membutuhkan waktu sekitar 40 menit.

Langkah kedua dan ketiga membutuhkan penggunaan paket matematika. Saya suka dan menggunakan MATLAB selama bertahun-tahun. Contoh saya membangun karakteristik aliran linierisasi dibuat di dalamnya. Sebuah contoh dapat diunduh dari tautan , jalankan dan secara mandiri mencari tahu metode membangun karakteristik aliran linier.

Karakteristik aliran untuk turbin yang dimaksud dibangun untuk nilai-nilai tetap dari parameter mode:

• operasi satu tahap
• tekanan uap tekanan sedang = 13 kgf / cm2,
• tekanan uap tekanan rendah = 1 kgf / cm2.

Isi dari arsip Chuchueva-PT-80-linier-karakteristik-curve.rar .

1) Nomogram konsumsi spesifik qt bruto untuk pembangkit listrik (titik merah bertanda didigitalkan - dipindahkan ke tabel):

• PT80_qt_Qm_eq_0_digit.png,
• PT80_qt_Qm_eq_100_digit.png,
• PT80_qt_Qm_eq_120_digit.png,
• PT80_qt_Qm_eq_140_digit.png,
• PT80_qt_Qm_eq_150_digit.png,
• PT80_qt_Qm_eq_20_digit.png,
• PT80_qt_Qm_eq_40_digit.png,
• PT80_qt_Qm_eq_60_digit.png,
• PT80_qt_Qm_eq_80_digit.png.

2) Hasil digitalisasi (setiap file csv sesuai dengan file png):

• PT-80_Qm_eq_0.csv,
• PT-80_Qm_eq_100.csv,
• PT-80_Qm_eq_120.csv,
• PT-80_Qm_eq_140.csv,
• PT-80_Qm_eq_150.csv,
• PT-80_Qm_eq_20.csv,
• PT-80_Qm_eq_40.csv,
• PT-80_Qm_eq_60.csv,
• PT-80_Qm_eq_80.csv.

3) Skrip MATLAB dengan perhitungan dan grafik:

• PT_80_linear_characteristic_curve.m

4) Hasil digitalisasi nomogram dan hasil membangun karakteristik aliran linierisasi dalam bentuk tabel:

• PT_80_linear_characteristic_curve.xlsx.

Langkah 1. Terjemahan nomogram atau hasil pengukuran menjadi tampilan tabular

1. Sumber pengolahan data

Data awal untuk contoh kami adalah nomograms q _t gross.

Untuk mendigitalkan banyak nomogram, Anda memerlukan alat khusus. Saya telah berulang kali menggunakan aplikasi web untuk tujuan ini. Aplikasi ini sederhana, nyaman, tetapi tidak memiliki fleksibilitas yang cukup untuk mengotomatisasi proses. Bagian dari pekerjaan harus dilakukan secara manual.

Pada langkah ini, penting untuk mendigitalkan titik-titik ekstrem nomogram yang menentukan batas rentang penyesuaian turbin uap .

Tugasnya adalah untuk menandai titik karakteristik debit di setiap file png menggunakan aplikasi , mengunduh csv yang dihasilkan dan mengumpulkan semua data dalam satu tabel. Hasil digitalisasi dapat ditemukan dalam file PT-80-linear-Characteristic-curve.xlsx, sheet “PT-80”, table “Input data”.

2. Membawa satuan ukuran ke satuan daya

Selanjutnya, pada lembar "PT-80" kami menghitung nilai Q ₀ sesuai dengan rumus

$$$$ tampilkan $$ \ mulai {persamaan} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad (1) \ end {persamaan} $$ tampilkan $$

dan kami membawa semua nilai awal ke MW. Perhitungan diimplementasikan menggunakan MS Excel.

Tabel yang dihasilkan "Input data (unit power)" adalah hasil dari langkah pertama algoritma.

Langkah 2. Linearisasi karakteristik aliran turbin uap

1. Menguji MATLAB

Pada langkah ini, Anda perlu menginstal dan membuka versi MATLAB tidak kurang dari 7,3 (ini adalah versi lama, saat ini 8,0). Dalam MATLAB buka file PT_80_linear_characteristic_curve.m, jalankan dan pastikan itu berfungsi. Semuanya berfungsi dengan benar, jika pada hasil menjalankan skrip pada baris perintah Anda melihat pesan berikut:

    PT_80_linear_characteristic_curve.xlsx  1  : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874   = 0.006, (0.57%)      = 37 

Jika Anda memiliki kesalahan, cari tahu sendiri cara memperbaikinya.

2. Perhitungan

Semua perhitungan diimplementasikan dalam file PT_80_linear_characteristic_curve.m. Mari kita pertimbangkan di beberapa bagian.

1) Kami menunjukkan nama file sumber, lembar, rentang sel yang berisi tabel "Sumber data (unit kapasitas)" yang diperoleh pada langkah sebelumnya.

 XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334'; 

2) Kami membaca sumber data di MATLAB.

 sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf('    %s  %1.0f \n', XLSFileName, toc); 

Kami menggunakan variabel Qm untuk laju aliran rata-rata uap _Qp , indeks m dari tengah adalah rata-rata; sama halnya, kami menggunakan variabel Ql untuk aliran uap tekanan rendah Q _n , indeks l dari rendah adalah rendah.

3) Tentukan koefisien α _i .

Ingat rumus umum untuk karakteristik aliran

$$$$ menampilkan $$ \ mulai {persamaan} Q_0 = f (N, Q_, Q_) \ qquad (2) \ end {persamaan} $$ menampilkan $$

dan tentukan variabel independen (x_digit) dan dependen (y_digit).

 x_digit = [N Qm Ql ones(size(N,1),1)]; %  N,   Q,   Q,   y_digit = Q0; %    Q0 

Jika Anda tidak mengerti mengapa matriks x_digit memiliki vektor tunggal (kolom terakhir), maka bacalah materi regresi linier. Pada topik analisis regresi, saya merekomendasikan buku Draper N., Smith H. Analisis regresi terapan . New York: Wiley, In press, 1981. 693 hal. (tersedia dalam bahasa Rusia).

Persamaan karakteristik aliran linier dari turbin uap

$$$$ menampilkan $$ \ mulai {persamaan} Q_0 = \ alpha_N \ cdot N + \ alpha_ \ cdot Q_ + \ alpha_ \ cdot Q_ + \ alpha_0 \ qquad (3) \ end {persamaan} $$ menampilkan $$

adalah model regresi linier berganda. Koefisien α _i akan ditentukan dengan menggunakan "manfaat besar peradaban" - metode kuadrat terkecil. Secara terpisah, saya perhatikan bahwa metode kuadrat terkecil dikembangkan oleh Gauss pada 1795.

Dalam MATLAB, ini dilakukan dalam satu baris.

 A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A); 

Variabel A berisi koefisien yang diinginkan (lihat pesan pada baris perintah MATLAB).

Dengan demikian, karakteristik aliran turunan uap PT-80 yang diperoleh memiliki bentuk

$$$$ tampilkan $$ \ mulai {persamaan} Q_0 = 2.317 \ cdot N + 0.621 \ cdot Q_ + 0.255 \ cdot Q_ + 33.874 \ qquad (4) \ end {persamaan} $$ display $$

4) Kami memperkirakan kesalahan linierisasi dari karakteristik aliran yang diperoleh.

 y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf('  = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100); 

Kesalahan linearisasi adalah 0,57% (lihat pesan pada baris perintah MATLAB).

Untuk menilai kenyamanan penggunaan karakteristik aliran turbin uap, kami memecahkan masalah menghitung laju aliran uap tekanan tinggi Q ₀ pada nilai beban yang diketahui N, Q _p , _Qt .

Misalkan N = 82,3 MW, Q _p = 55,5 MW, Qt = 62,4 MW, lalu

$$$$ menampilkan $$ \ mulai {persamaan} Q_0 = 2.317 \ cdot 82.3 + 0.621 \ cdot 55.5 + 0.255 \ cdot 62.4 + 33.874 = 274.9 \ qquad (5) \ end {persamaan} $$ tampilkan $$

Biarkan saya mengingatkan Anda bahwa kesalahan perhitungan rata-rata adalah 0,57%.

Mari kita kembali ke pertanyaan, mengapa karakteristik aliran linier dari turbin uap pada dasarnya lebih nyaman daripada nomogram konsumsi spesifik qt gross untuk pembangkit listrik? Untuk memahami perbedaan mendasar dalam praktik, pecahkan dua masalah.

1. Hitung Q ₀ dengan akurasi yang ditunjukkan menggunakan nomogram dan mata Anda.
2. Mengotomatiskan proses penghitungan Q ₀ menggunakan nomogram.

Jelas, dalam tugas pertama, penentuan nilai kotor q oleh mata penuh dengan kesalahan kotor.

Tugas kedua rumit untuk diotomatisasi. Karena nilai q q adalah sangat nonlinier , untuk otomasi seperti itu, jumlah titik digital sepuluh kali lebih besar dari pada contoh saat ini. Digitalisasi saja tidak cukup, perlu juga menerapkan algoritma untuk interpolasi (menemukan nilai antar titik) dari nilai kotor non-linear.

Langkah 3. Menentukan batas kisaran penyesuaian turbin uap

1. Perhitungan

Untuk menghitung rentang penyesuaian, kita akan menggunakan "good of civilization" lainnya - metode convex hull, convex hull.

Di MATLAB, ini dilakukan sebagai berikut.

 indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf('     = %d\n\n', size(index,1)); 

Metode convhull () menentukan titik batas rentang penyesuaian yang diberikan oleh nilai-nilai variabel N, Qm, Ql. Indeks variabelCH berisi simpul segitiga yang dibangun menggunakan triangulasi Delaunay. Variabel regRange berisi titik batas dari rentang penyesuaian; variabel regRangeQ0 - laju aliran uap tekanan tinggi untuk titik batas rentang kendali.

Hasil perhitungan dapat ditemukan di file PT_80_linear_characteristic_curve.xlsx, sheet “PT-80-result”, tabel “Batas rentang penyesuaian”.

Karakteristik aliran linierisasi dibangun. Ini adalah rumus (4) dan 37 poin yang menentukan batas (shell) dari rentang penyesuaian dalam tabel terkait.

2. Verifikasi

Saat mengotomatiskan proses perhitungan, Q ₀ perlu memeriksa apakah suatu titik dengan nilai N, _Qp , _{Qt berada} di dalam rentang penyesuaian atau di luarnya (mode ini tidak layak secara teknis). Di MATLAB, ini bisa dilakukan sebagai berikut.

Kami menetapkan nilai N, _Qp , _Qt yang ingin kami periksa.

 n = 75; qm = 120; ql = 50; 

Kami periksa.

 in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f     \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f      ( )\n', n, qm, ql); end 

Verifikasi dilakukan dalam dua langkah:

• variabel in1 menunjukkan apakah nilai N, _Qp telah jatuh ke proyeksi shell pada sumbu N, _Qp ;
• sama halnya, variabel in2 menunjukkan apakah nilai-nilai _Qp , _{Qt berada} di dalam proyeksi shell pada sumbu _Qp , _Qt .

Jika kedua variabel sama dengan 1 (benar), maka titik yang diinginkan ada di dalam shell, yang menetapkan rentang penyesuaian turbin uap.

Ilustrasi karakteristik aliran linier yang diperoleh dari turbin uap

“Manfaat paling dermawan dari peradaban” kami dapatkan dalam hal menggambarkan hasil perhitungan.

Pertama-tama kita harus mengatakan bahwa ruang tempat kita membuat grafik, yaitu ruang dengan sumbu x - N, y - _Qt , z - Q ₀ , w - _Qp , disebut ruang rejim (lihat Optimasi operasi pembangkit listrik termal dalam kondisi pasar grosir listrik dan kapasitas Rusia

) Setiap titik ruang ini mendefinisikan mode operasi turbin uap tertentu. Mode mungkin

• layak secara teknis, jika intinya ada di dalam shell yang menentukan rentang penyesuaian,
• secara teknis tidak layak jika intinya berada di luar shell ini.

Jika kita berbicara tentang mode kondensasi pengoperasian turbin uap ( _Qp = 0, _Qt = 0), maka karakteristik aliran yang dilinearisasi adalah segmen garis lurus . Jika kita berbicara tentang turbin tipe T, maka karakteristik aliran linierisasi adalah poligon datar dalam ruang rezim tiga dimensi dengan sumbu x - N, y - _Qt , z - Q ₀ , yang mudah divisualisasikan. Untuk turbin tipe PT, visualisasi adalah yang paling sulit, karena karakteristik aliran yang linierisasi dari turbin tersebut adalah poligon datar dalam ruang empat dimensi (untuk penjelasan dan contoh, lihat Mengoptimalkan pengoperasian pembangkit listrik termal di pasar grosir dan tenaga listrik Rusia, bagian Linearisasi karakteristik aliran turbin ).

1. Ilustrasi karakteristik aliran linier yang diperoleh dari turbin uap

Mari kita membangun nilai-nilai tabel "Input data (unit daya)" di ruang rezim.

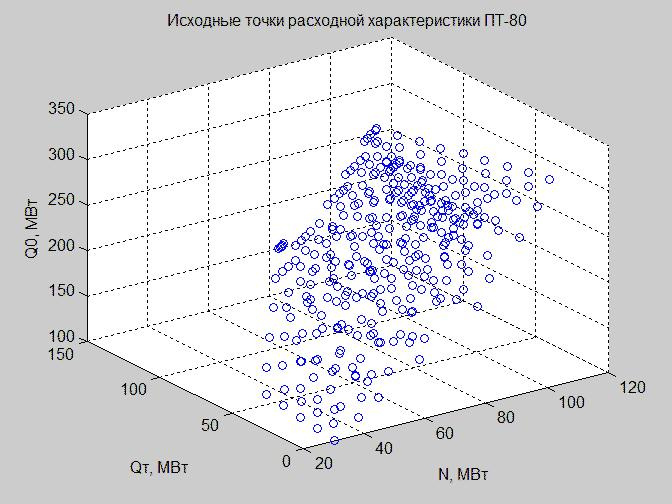
Fig. 3. Titik awal karakteristik aliran dalam ruang rezim dengan sumbu x - N, y - _Qt , z - Q ₀

Karena kita tidak dapat membangun ketergantungan dalam ruang empat dimensi, kita belum mencapai peradaban yang baik, kita beroperasi pada nilai-nilai Q _n sebagai berikut: tidak termasuk (Gbr. 3), fix (Gbr. 4) (lihat kode untuk membuat grafik di MATLAB).

Kami memperbaiki nilai _Qp = 40 MW dan membangun titik awal dan karakteristik aliran linierisasi.

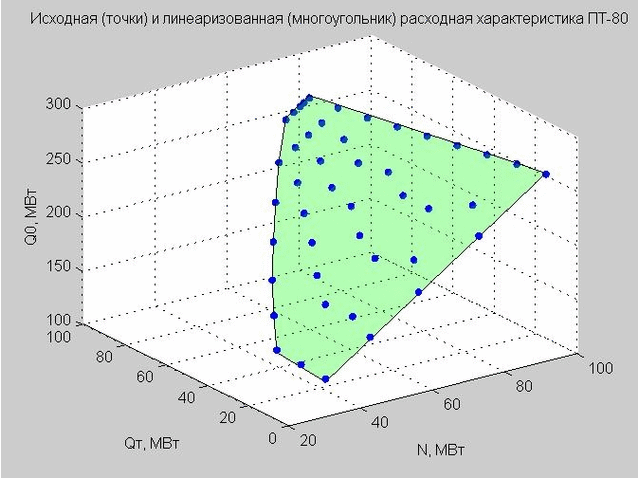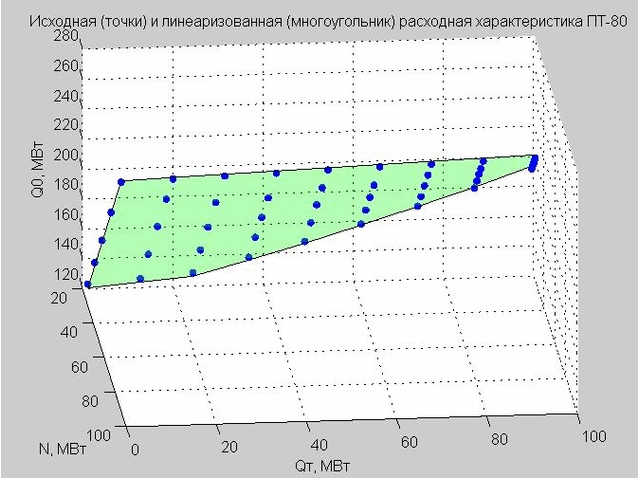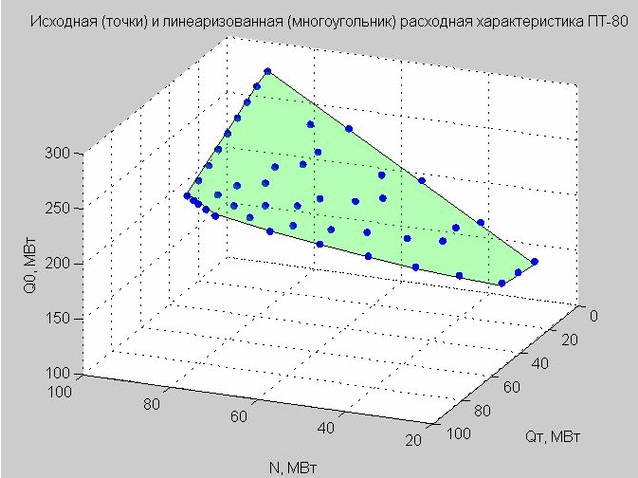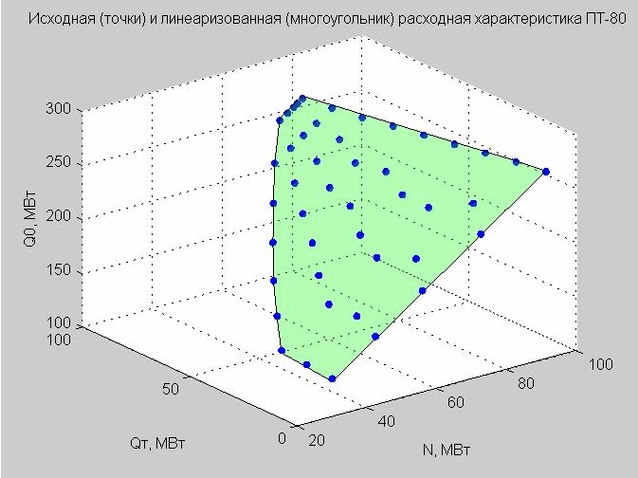
Fig. 4. Titik awal karakteristik pelepasan (titik biru), karakteristik pelepasan linierisasi (poligon datar hijau)

Mari kita kembali ke rumus karakteristik laju aliran linier (4) yang kami peroleh. Jika kita memperbaiki Q _p = 40 MW MW, maka rumus akan memiliki formulir

$$$$ menampilkan $$ \ mulai {persamaan} Q_0 = 2.317 \ cdot N + 0.255 \ cdot Q_T + 58.714 \ qquad (6) \ end {persamaan} $$ menampilkan $$

Model ini mendefinisikan poligon datar dalam ruang tiga dimensi dengan sumbu x - N, y - _Qt , z - Q ₀ dengan analogi dengan turbin tipe-T (kita melihatnya pada Gambar 4).

Beberapa tahun yang lalu, ketika q nomograms kotor dikembangkan, kesalahan mendasar dibuat pada tahap analisis data awal. Alih-alih menerapkan metode kuadrat terkecil dan membangun karakteristik aliran linier dari turbin uap untuk alasan yang tidak diketahui, mereka membuat perhitungan primitif:

$$$$ menampilkan $$ \ mulai {persamaan} Q_0 (N) = Q_ = Q_0 - Q_ - Q_ \ qquad (7) \ end {persamaan} $$ menampilkan $$

Dikurangi dari laju aliran uap tekanan tinggi Q ₀ laju aliran uap _Qt , _Qp dan mengaitkan perbedaan yang dihasilkan Q ₀ (N) = Q _e dengan pembangkit listrik. Nilai yang diperoleh Q ₀ (N) = Q _e dibagi dengan N dan dikonversi ke kcal / kW · h, setelah menerima konsumsi spesifik qt bruto. Perhitungan ini tidak sesuai dengan hukum termodinamika.

Pembaca yang budiman, mungkin Anda tahu alasan yang tidak diketahui? Bagikan itu!

2. Ilustrasi kisaran penyesuaian turbin uap

Mari kita lihat cangkang kisaran penyesuaian di ruang rezim. Titik awal untuk konstruksinya disajikan pada Gambar. 5. Ini adalah poin yang sama yang kita lihat dalam gambar. 3, namun, parameter Q ₀ sekarang dikecualikan.

Fig. 5. Titik awal karakteristik aliran dalam ruang rejim dengan sumbu x - N, y - _Qp , z - _Qt

Banyak poin dalam ara. 5 adalah cembung. Menggunakan fungsi convexhull (), kami mendefinisikan titik-titik yang menentukan kulit terluar dari set ini.

Delaunay triangulation (satu set segitiga terhubung) memungkinkan kita untuk membangun cangkang dari kisaran penyesuaian. Verteks segitiga adalah nilai batas rentang penyesuaian turbin uap PT-80 yang sedang dipertimbangkan.

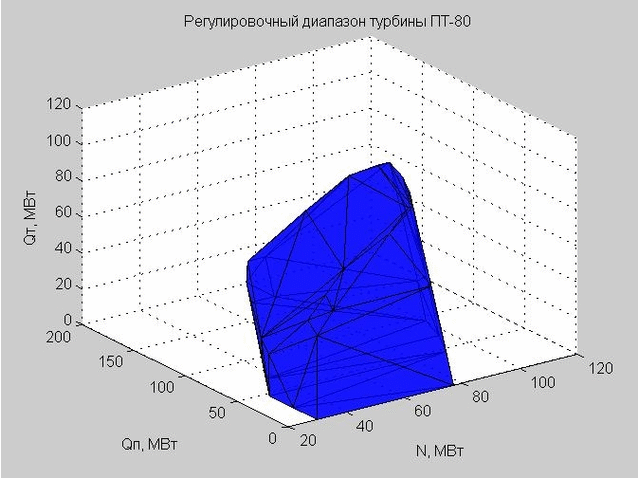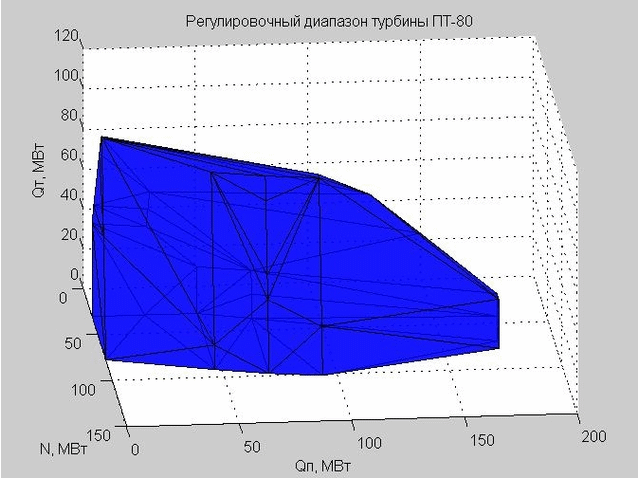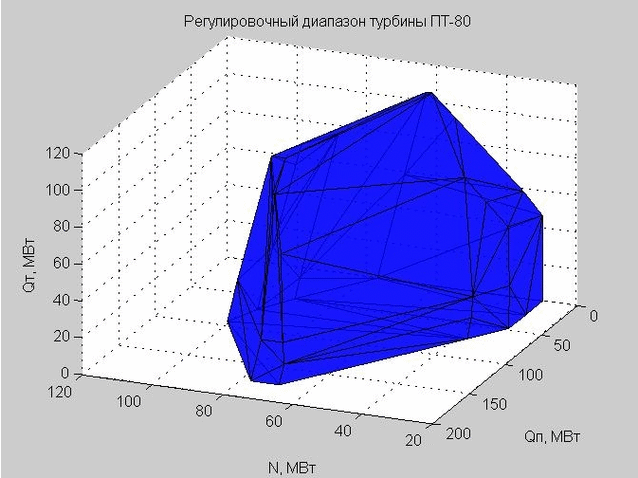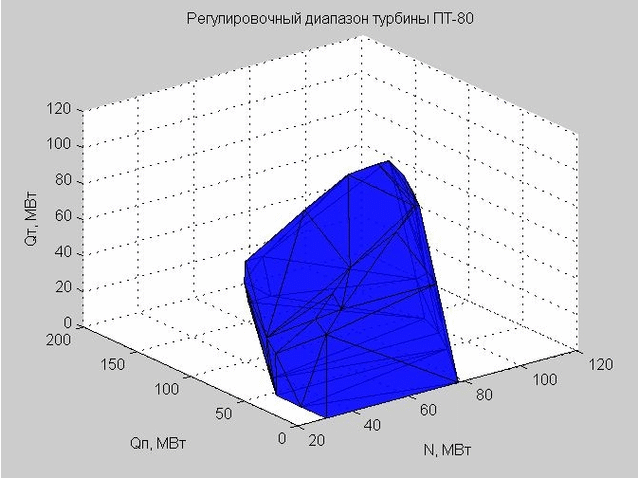
Fig. 6. Cangkang rentang penyesuaian, diwakili oleh banyak segitiga

Ketika kami melakukan pemeriksaan pada titik tertentu untuk masuk ke dalam rentang penyesuaian, kami memeriksa apakah titik ini terletak di dalam atau di luar shell yang dihasilkan.

Semua grafik yang disajikan di atas dibuat menggunakan alat MATLAB (lihat PT_80_linear_characteristic_curve.m).

Tugas yang menjanjikan terkait dengan analisis operasi turbin uap menggunakan karakteristik aliran linierisasi

Jika Anda sedang melakukan diploma atau disertasi, saya dapat menawarkan kepada Anda beberapa tugas, hal baru ilmiah yang dapat Anda buktikan dengan mudah ke seluruh dunia. Selain itu, Anda akan melakukan pekerjaan yang sangat baik dan bermanfaat.

Tugas 1

Tunjukkan bagaimana poligon rata berubah ketika tekanan uap tekanan rendah Qt berubah.

Tugas 2

Tunjukkan bagaimana poligon datar berubah ketika tekanan dalam kondensor berubah.

Tugas 3

Periksa apakah koefisien karakteristik aliran linierisasi dapat direpresentasikan sebagai fungsi parameter tambahan rezim, yaitu:

$$$$ menampilkan $$ \ begin {persamaan} \ alpha_N = f (p_ {0}, ...); \\ \ alpha_P = f (p_ {P}, ...); \\ \ alpha_T = f (p_ {T}, ...); \\ \ alpha_0 = f (p_ {2}, ...). \ end {persamaan} $$ menampilkan $$

Di sini p ₀ adalah tekanan uap tekanan tinggi, p _p adalah tekanan uap tekanan sedang, pt adalah tekanan uap tekanan rendah, p ₂ adalah tekanan uap buang di kondensor, semua unit adalah kgf / cm2.

Benarkan hasilnya.

Referensi

Chuchueva I.A., Inkina N.E. Optimalisasi CHP dalam kondisi pasar grosir tenaga listrik dan kapasitas Rusia // Sains dan Pendidikan: Edisi Ilmiah MSTU. N.E. Bauman. 2015. No. 8. S. 195-238.

• Bagian 1. Pernyataan substantif tentang masalah optimalisasi operasi CHP di Rusia
  
• Bagian 2. Linierisasi karakteristik aliran turbin
  
• Bagian 3. Pernyataan formal tentang masalah optimasi jangka pendek dari operasi CHPP di pasar industri tenaga listrik
  
• Bagian 4. Eksperimen Komputasi
  
• Referensi dengan komentar
  
• Perbandingan tugas pengoptimalan 1 dan 2 dalam menentukan komposisi optimal dari peralatan yang disertakan

Chuchueva I.A. Metode komputasi untuk menentukan konsumsi spesifik bahan bakar setara pembangkit listrik termal untuk energi listrik dan termal yang dipasok dalam mode generasi gabungan // Sains dan Pendidikan: Publikasi ilmiah MSTU. N.E. Bauman. 2016. No. 2. P. 135-165.

• Bagian 1. Pernyataan masalah
  
• Bagian 2. Ikhtisar Metode
  
• Bagian 3. Metode baru untuk menghitung konsumsi spesifik bahan bakar setara
  
• Bagian 4. Perbandingan Metode
  
• Referensi
  

Karakteristik aliran linier dari turbin uap.

• Bagian 1. Masalah Utama
  
• Bagian 2. Contoh konstruksi untuk turbin PT-80 di MATLAB
  
• Bagian 3. Menghilangkan mitos tentang mode operasi turbin uap