Massa, energi, momentum, dan hukum konservasi

Banyak sifat yang tidak jelas di dunia dikaitkan dengan sifat massa dan energi (serta momentum). Kita semua mendengar kata-kata ini, dan banyak dari kita memiliki gagasan yang kabur tentang maknanya. Tentu saja, makna kata "massa" dan "energi" dalam bahasa Inggris dan bahasa lainnya banyak. Sayangnya, tidak satu pun dari mereka bertepatan dengan yang ada dalam pikiran fisikawan. Cobalah untuk mengesampingkan makna kata-kata ini dan bekerja dengan konsep fisik yang tepat - jika tidak, Anda akan benar-benar bingung.

Perlu dicatat bahwa seseorang seharusnya tidak mengingat pasangan populer lain, "substansi dan energi" dengan frasa "massa dan energi". Banyak orang menyebut ungkapan terakhir seolah-olah materi dan energi adalah dua sisi dari koin yang sama. Tapi ini tidak benar. Materi dan energi termasuk dalam kategori yang berbeda, seperti apel dan orangutan. Sebuah substansi, tidak peduli bagaimana mendefinisikannya, adalah kelas objek yang ada di Alam Semesta, dan massa dan energi bukanlah objek, tetapi properti yang dimiliki objek-objek ini. Massa dan energi saling terkait satu sama lain, dan layak mendapat penjelasan umum.

Untuk memahami massa dan energi, Anda perlu menambahkan momentum kepada mereka dan mendiskusikan perbedaan dan hubungan kuantitas-kuantitas ini.

Energi

Kata "energi" memiliki banyak arti. Ketika kita sakit, kita mengatakan bahwa kita tidak memiliki energi yang tersisa, mengacu pada kekuatan dan motivasi. Ketika kita mengatakan bahwa seseorang penuh energi, yang kita maksud adalah aktivitasnya yang tinggi. Kami mengeluh tentang kenaikan harga energi, mengacu pada bahan bakar. Kita berbicara tentang energi spiritual sebagai sesuatu yang tak terukur, tetapi penting, mungkin semacam karisma. Dan semua konsep ini tumpang tindih satu sama lain, jadi kami memilih satu kata untuk menggambarkannya. Tetapi dalam fisika, energi adalah hal yang sangat berbeda. Dari sudut pandang fisika, salah satu definisi ini akan keliru dikacaukan dengan fisik. Dalam fisika, seseorang harus mematuhi istilah fisik agar tidak mendapatkan jawaban yang salah dan tidak sepenuhnya bingung.

Sayangnya, konsep "energi" dalam fisika sangat sulit digambarkan seperti halnya kamus - dengan frasa bermakna pendek. Tetapi jangan berpikir buruk - semuanya adalah ketidaksempurnaan bahasa alami, dan bukankah konsep energi dalam fisika tidak jelas. Dalam sistem fisik apa pun, sangat jelas apa energinya, baik dalam arti pengukuran eksperimental dan dalam arti perhitungan (jika ada persamaan yang menggambarkan sistem).

Salah satu alasan mengapa energi sangat sulit untuk dijelaskan adalah bahwa ia dapat mengambil banyak bentuk, dan tidak semuanya mudah dipahami. Berikut adalah tiga varietas umum:

1. Energi dapat tertutup dalam massa suatu benda. Di sini saya menyebut opsi ini "energi massa" (berkat persamaan terkenal E = mc ^2, energi mengikat massa. Ini juga disebut "energi istirahat", karena ini adalah energi dari suatu objek saat istirahat, yaitu, tanpa gerakan).

2. Kedua, energi dikaitkan dengan pergerakan suatu objek. Di sini saya menyebutnya "energi gerak", dan istilah teknis untuk ini adalah energi kinetik. Opsi ini mudah dipahami secara intuitif, karena objek yang bergerak cepat memiliki lebih banyak energi daripada yang bergerak lambat. Selain itu, benda berat memiliki lebih banyak energi gerakan daripada benda ringan yang bergerak dengan kecepatan yang sama.

3. Energi dapat disimpan dalam hubungan objek (dan biasanya disebut "potensial"). Ia disimpan dalam pegas yang terentang, di dalam air di belakang bendungan, dalam interaksi gravitasi Bumi dan Matahari, dalam interaksi atom-atom dalam molekul. Ada banyak cara untuk menyimpan energi. Kedengarannya kabur, tapi bahasanya harus disalahkan. Dalam setiap kasus ini, ada rumus tepat yang menggambarkan energi yang tersimpan dalam sistem dan cara yang tepat untuk mengukurnya.

Jenis energi ketiga terhubung dengan apa yang saya sebut energi interaksi, dan ini adalah konsep yang paling membingungkan dari semuanya. Berbeda dengan energi massa dan energi gerak, yang selalu lebih besar atau sama dengan nol, energi interaksi bisa positif dan negatif. Sejauh ini saya akan meninggalkan topik ini, tetapi kami akan kembali ke topik ini.

Energi adalah jumlah khusus yang sangat penting bagi fisika. Alasan pentingnya ini adalah bahwa hal itu "dilestarikan." Apa artinya ini?

Jika Anda memulai pengamatan dengan objek atau set objek - kami akan menyebutnya "sistem objek" - yang memiliki sejumlah energi pada saat awal (jangan lupa untuk menghitung semua energi - massa, gerakan, energi yang tersimpan dari semua jenis, dll.), Dan kemudian bagian-bagian dari sistem hanya akan berinteraksi satu sama lain dan tidak ada yang lain, maka pada akhir pengamatan jumlah total energi yang dimiliki oleh benda-benda ini akan sama dengan di awal. Energi total sistem dilestarikan - jumlah totalnya tidak berubah. Ini bisa berubah bentuk, tetapi jika Anda melacak semua varietas, maka pada akhirnya akan sama seperti pada awalnya.

Aturan ini berfungsi bahkan jika beberapa objek menghilang dan memberi jalan kepada yang lain, misalnya, jika satu partikel dalam sistem meluruh menjadi dua lainnya bergabung ke dalam sistem.

Mengapa energi dihemat? Karena prinsip matematis, menghubungkan fakta bahwa hukum-hukum alam tidak berubah dari waktu ke waktu, dengan keberadaan kuantitas yang dilestarikan, yang menurut definisi kita sebut "energi".

Kami berutang definisi paling terkenal dan umum dari prinsip ini kepada Emmy Noether , salah satu fisikawan matematika terhebat di abad sebelumnya, seorang kontemporer dari Einstein. Beberapa anggota komunitas fisik dan matematika memperlakukannya dengan rasa hormat yang dalam , tetapi pada waktu itu di negara asalnya Jerman ia menderita diskriminasi berdasarkan jenis kelamin dan kebangsaan (di sana mereka memblokir upaya untuk memberinya gelar profesor di Göttingen , dan dari sana ia harus melarikan diri setelah Nazi berkuasa). Setelah beremigrasi ke Amerika Serikat, setelah hanya dua tahun mengajar di Brin-Mar College (yang hingga hari ini hanya menerima wanita untuk pelatihan), ia meninggal karena kanker.

Teorema Noether yang terkenal (sebenarnya ini adalah dua teorema yang berkaitan erat) memberi tahu kita bahwa jika ada simetri dalam hukum-hukum alam - dalam kasus kami, ini berarti bahwa hukum-hukum alam sama pada setiap saat waktu - ini menyiratkan konservasi jumlah tertentu - dalam kasus kami, energi .

Terlebih lagi, teorema memberi tahu kita dengan tepat besaran besarnya - apa saja bentuk energi yang berbeda untuk sistem objek tertentu yang perlu ditambahkan untuk mendapatkan energi total. Itulah mengapa fisikawan selalu tahu persis apa energi itu, dan mengapa lebih mudah diperoleh dengan menggunakan persamaan daripada mendefinisikan dalam kata-kata.

Impuls

Situasi dengan momentum kira-kira sama dengan energi. Hukum alam sama di mana-mana. Secara kasar, percobaan memberikan jawaban yang sama, apakah Anda menghabiskannya di utara atau selatan dari sini, barat atau timur, di atas bangunan atau di poros yang dalam. Pilih arah mana pun di ruang angkasa. Kemudian, menurut Noether, momentum sepanjang arah ini dilestarikan. Karena ada tiga dimensi dalam ruang, dimungkinkan untuk bergerak dalam tiga arah independen yang berbeda dan ada tiga hukum konservasi independen. Anda dapat memilih tiga arah, asalkan berbeda. Misalnya, Anda dapat memilih pulsa di arah utara-selatan, barat-timur, dan naik-turun sebagai tiga undang-undang konservasi. Atau Anda dapat memilih tiga lainnya - ke arah ke dan dari Matahari, di sepanjang orbit Bumi di kedua arah, dan naik turun dalam kaitannya dengan bidang tata surya. Pilihan Anda tidak masalah, karena momentum disimpan sepanjang arah.

Bentuk impuls yang paling sederhana muncul karena gerakan sederhana dari objek, dan ini adalah sesuatu yang dapat dibayangkan secara intuitif: jika suatu objek bergerak ke arah tertentu, maka ia memiliki impuls ke arah ini, dan semakin cepat bergerak, semakin besar impuls ini. Dan benda yang lebih berat memiliki momentum lebih besar daripada benda ringan jika bergerak dengan kecepatan yang sama.

Salah satu konsekuensi menarik dari konservasi ini: jika Anda memiliki sistem objek yang tidak bergerak (yaitu, sistem secara keseluruhan tidak bergerak jika Anda meratakan semua gerakan objek penyusunnya), maka ia akan tetap tak bergerak, kecuali jika diberikan gerakan eksternal apa pun dampak. Alasannya adalah bahwa dalam sistem tetap, momentum total adalah nol, dan karena momentum dijaga, momentum itu akan tetap nol selamanya kecuali ada sesuatu yang mengintervensi dari luar sistem.

Massa, dan hubungannya dengan energi dan momentum

Sekarang mari kita beralih ke misa

Sayangnya, banyak kebingungan dikaitkan dengan massa - setelah publikasi karya Einstein tentang teori relativitas untuk beberapa waktu ada dua konsep massa. Dan hanya satu dari mereka (yang di mana Einstein sendiri berhenti, dan yang kadang-kadang disebut "massa invarian" atau "massa istirahat" untuk membedakannya dari istilah "massa relativistik" yang sudah menjadi kuno, masih digunakan dalam fisika partikel. Dalam artikel terpisah saya akan menjelaskan ini secara lebih rinci.


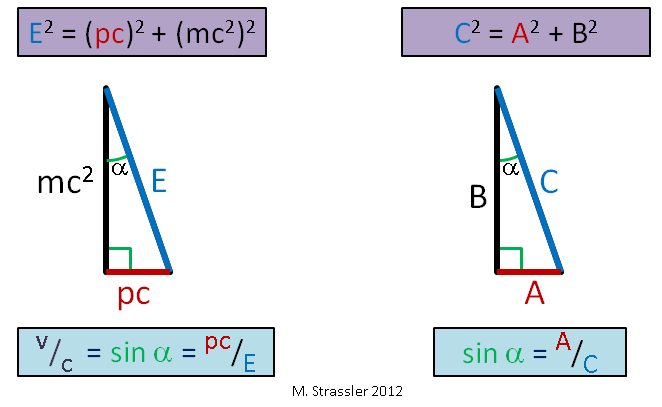Fig. 1

Massa m, yang saya gunakan dalam artikel, berarti massa yang secara langsung mengikat energi dan momentum. Untuk objek yang bergerak tanpa pengaruh kekuatan eksternal (tidak berinteraksi secara signifikan dengan objek lain), Einstein menyarankan (dan ini dikonfirmasi oleh eksperimen) bahwa energi E, momentum p, dan massa m memenuhi persamaan Pythagoras sederhana:

$$ $$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (persamaan No. 1)$$

Ingat Pythagoras tua yang mengklaim bahwa untuk segitiga siku-siku dengan sisi A dan B dan sisi miring C, persamaan $$$C ^ 2 = A ^ 2 + B ^ 2$ ? Ini adalah koneksi dengan tipe yang sama - lihat gbr. 1. Bersama kami, c adalah kecepatan konstan, yang, seperti akan kita lihat, berfungsi sebagai batas kecepatan universal. Kita juga akan melihat mengapa itu disebut "kecepatan cahaya."

Menurut persamaan Einstein, kecepatan objek dibagi dengan batas kecepatan c hanya rasio pc ke E:

$$ $$v / c = (p c) / E \ qquad (persamaan # 2)$$

Artinya, rasio kaki horizontal dengan sisi miring. Ini juga sama dengan sinus sudut α pada Gambar. 1. Jadi di sini, warga negara. Dan karena kaki dari segitiga siku-siku selalu lebih pendek dari sisi miring (sinus dari sudut apa pun selalu kurang dari atau sama dengan 1), kecepatan benda apa pun tidak dapat melebihi s, batas kecepatan universal. Dengan peningkatan kecepatan objek bermassa tetap, p dan E menjadi sangat besar (Gbr. 2), tetapi E selalu lebih besar dari pc, jadi v selalu kurang dari c!


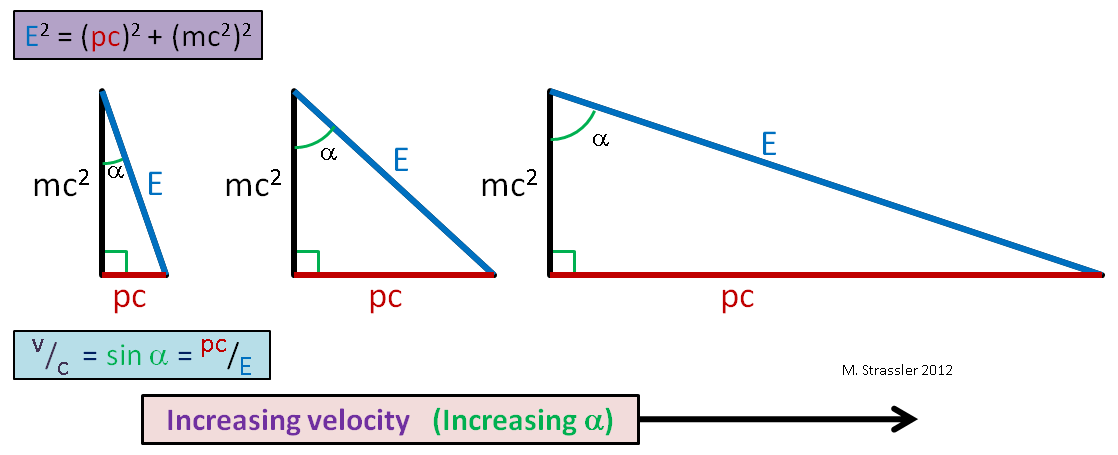Fig. 2

Sekarang perhatikan bahwa jika objek tidak bergerak, maka momentumnya p sama dengan nol, dan rasio dalam persamaan 1 berkurang menjadi:

$$ $$E ^ 2 = (mc ^ 2) ^ 2, \ quad atau \ quad E = mc ^ 2$$

Formula Einstein yang terkenal, hubungan massa dengan jumlah energi yang tetap (apa yang saya sebut energi massa), hanyalah pernyataan yang sesuai dengan fakta bahwa ketika sebuah segitiga berubah menjadi garis vertikal, seperti pada Gambar. 3 di sebelah kiri, sisi miringnya menjadi panjang yang sama dengan kaki vertikal. Pada saat yang sama, itu tidak berarti bahwa energi selalu sama dengan massa kali kuadrat. Ini hanya berfungsi untuk objek istirahat dengan momentum nol.


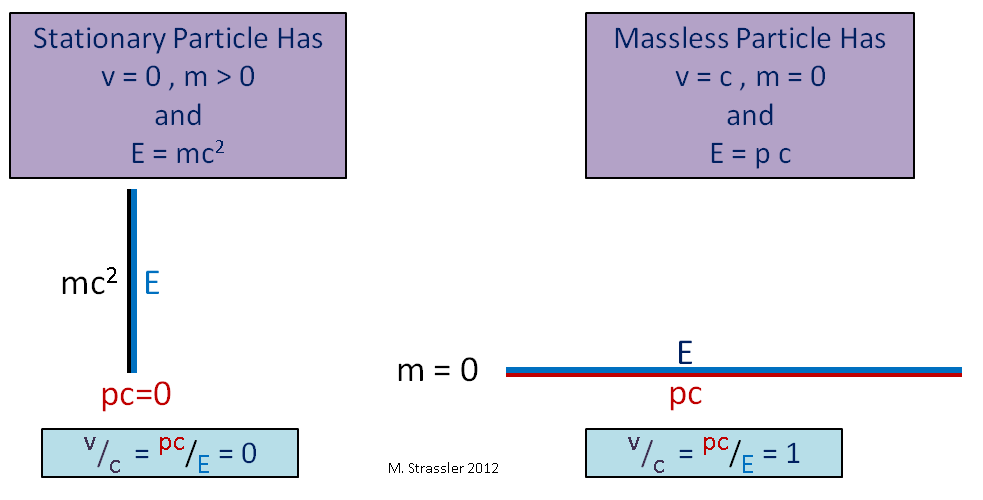Fig. 3

Pengamatan lain yang menarik: untuk partikel tanpa massa, kaki vertikal segitiga adalah nol, dan kaki miring dan horisontal adalah sama, seperti pada Gambar. 3. Dalam hal ini, E adalah pc, yang berarti bahwa v / c = 1, atau v = c. Terlihat bahwa partikel tak bermassa (misalnya, foton, partikel cahaya) tak terhindarkan bergerak dengan kecepatan c. Oleh karena itu, kecepatan cahaya sama dengan batas kecepatan universal, s.

Di sisi lain, jika kita mengambil partikel dengan massa, seperti pada Gambar. 4, tidak masalah seberapa besar Anda membuat momentum dan energi, E akan selalu sedikit lebih dari p * c, sehingga kecepatan akan selalu kurang dari s. Partikel tak bermassa harus bergerak dengan kecepatan maksimum. Kecepatan partikel masif seharusnya lebih sedikit.


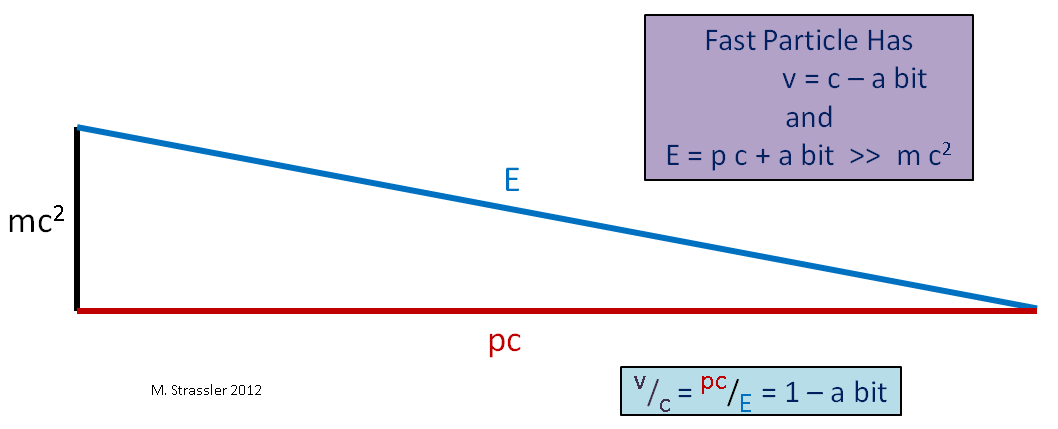Fig. 4. Di sini ">>" berarti "lebih banyak"

Bayangkan kasing lain, objek besar yang bergerak perlahan (dibandingkan dengan kecepatan cahaya), seperti mobil. Karena kecepatan v jauh lebih kecil dari c, momentumnya p kali c akan jauh lebih sedikit daripada E, dan, seperti yang dapat dilihat dari Gambar. 5, E akan menjadi sedikit lebih dari mc ² . Oleh karena itu, energi gerak benda lambat E - mc ² jauh lebih sedikit daripada energi massa mc ² , dan untuk benda cepat energi gerak dapat dibuat besar secara sewenang - wenang, seperti yang kita lihat pada Gambar. 4.

Satu titik halus: momentum bukan hanya angka, tetapi juga vektor. Dia memiliki kekuatan dan arah. Ini diarahkan pada pergerakan partikel. Ketika saya menulis p, saya hanya menunjukkan nilainya. Dalam banyak kasus, perlu untuk melacak arah pulsa, meskipun dalam persamaan No. 1, yang menghubungkan pulsa dengan energi dan massa, ini tidak perlu.


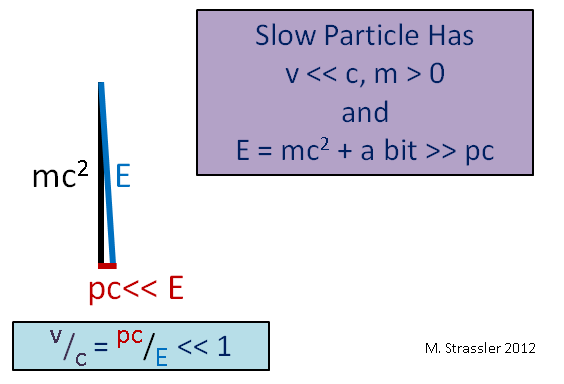Fig. 5

Poin halus lainnya: Saya menggunakan segitiga dan trigonometri sederhana, karena diketahui semua orang dari sekolah. Para ahli harus lebih berhati-hati - Anda dapat dengan benar memahami persamaan Einstein menggunakan fungsi hiperbolik yang biasanya tidak ditemukan oleh amatir, tetapi sangat penting untuk memahami struktur teori dan membuat hal-hal lebih dimengerti seperti penambahan kecepatan, kompresi jarak, dll. Orang yang tidak berpura-pura menjadi ahli dapat mengabaikan hal ini.

Tetapi apakah kecepatan relatif? ..

Jika Anda membaca teks dengan cermat, sesuatu mungkin sudah mengejutkan Anda. Anda tahu bahwa kecepatan partikel - atau apa pun yang bergerak lebih lambat dari cahaya - tergantung pada sudut pandangnya.

Jika Anda duduk di rumah dan membaca buku, Anda akan mengatakan bahwa kecepatan buku itu nol (dan itu benar-benar relatif terhadap Anda), oleh karena itu, ia tidak memiliki momentum dan energi gerak, hanya energi massa. Tetapi jika saya berdiri di bulan, saya akan mengingatkan Anda bahwa Bumi berputar, sehingga rotasi ini memikat Anda, dan menggerakkan Anda relatif terhadap saya dengan kecepatan ratusan kilometer per jam. Jadi Anda dan buku Anda akan memiliki dorongan dari sudut pandang saya.

Siapa yang benar

Varian relativitas menurut Galileo - prinsip pertama relativitas - menyatakan bahwa kita berdua benar. Varian relativitas Einstein setuju dengan sudut pandang Galileo bahwa keduanya benar, tetapi membuat penyesuaian penting tentang bagaimana pengikut Galileo akan menunjukkan energi, momentum dan massa buku, menempatkan jumlah-jumlah ini dalam hubungan Pythagoras dari persamaan No. 1.

Tetapi jika semuanya benar, E dan mana yang harus saya ganti dalam rasio energi / momentum / massa, $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ ? Pengganti E dan p diukur dengan Anda membaca buku, yaitu E = mc ² dan p = 0? Atau gantikan E dan p, yang dimiliki buku itu dari sudut pandang saya, ketika Anda bergerak dengan Bumi?

Jawaban atas pertanyaan ini berisi seluruh esensi dari persamaan Einstein No. 1. Setiap pengamat akan mengukur nilai E dan p untuk buku yang berbeda, tergantung pada seberapa cepat buku akan bergerak relatif terhadapnya. Tapi untuk semua pengamat persamaannya $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ akan benar!

Keajaiban! Namun pada kenyataannya, genius adalah sebuah ide yang muncul pada tahun 1905 tentang cara mengganti set persamaan yang diusulkan oleh Newton dan para pengikutnya dengan seperangkat persamaan baru yang menakjubkan, yang masih bertepatan dengan semua eksperimen sebelumnya, tetapi ternyata merupakan representasi kenyataan yang lebih akurat. Sulit membayangkan berapa banyak yang diperlukan untuk mengubah cara berpikir untuk memikirkannya sampai Anda mengetahui berapa banyak semuanya bisa salah selama pembentukan teori baru, dan berapa banyak persamaan lain yang mengandung kontradiksi dengan matematika atau dengan eksperimen sebelumnya, Anda dapat Itu akan menawarkan (dan orang-orang menawari mereka). Sebagai contoh, pekerjaan fisikawan pemula terus-menerus datang kepada saya, mencoba untuk "memperbaiki" persamaan Einstein, tetapi saya belum pernah melihat satupun dari mereka memeriksa persamaan mereka untuk konsistensi internal. Ini adalah tugas yang sangat sulit dan alasan kegagalan sebagian besar teori.

Tetapi bagaimana kemudian energi dan momentum dapat dilestarikan?

Tunggu sebentar, kata Anda, ketika kepala Anda siap meledak dan memercikkan segala sesuatu di sekitar Anda dengan otak Anda (saya ingat sensasi ini sendiri), tetapi energi dan momentum harus dilestarikan! Jadi bagaimana pengamat yang berbeda tidak setuju dengan apa mereka?

Bahkan ada lebih banyak sihir, yang, kebetulan, sebelum Einstein. Percayalah, Semesta adalah akuntan yang sangat, sangat pintar, dan terlepas dari kenyataan bahwa pengamat yang berbeda tidak akan menyetujui energi yang tersedia dalam suatu objek atau sistem objek, mereka semua akan setuju bahwa energi ini tidak berubah seiring waktu. Hal yang sama berlaku untuk momentum.

Tetapi massa sangat berbeda dari energi dan momentum. Pertama, massa tidak dilestarikan. Di alam, ada banyak proses yang mengubah massa total suatu sistem: misalnya, partikel Higgs besar dapat membusuk menjadi dua foton tak bermassa. Tidak ada simetri yang dikaitkan dengan massa, dan karenanya Noether tidak memiliki hukum konservasi untuk kita. Kedua, tidak seperti energi dan momentum, yang nilainya tergantung pada pengamat (khususnya, pada kecepatannya sehubungan dengan objek yang diukur), semua pengamat akan setuju dengan massa m objek. Dan ini sama sekali tidak jelas, dan terjadi karena persamaan Einstein bekerja dengan sangat cerdik.

Jadi apa yang kita miliki

Saat ini, kami memiliki beberapa pengetahuan yang saling bertentangan. Kita tahu itu:

• Energi dan momentum sistem fisik yang terisolasi dilestarikan (energi total dan momentum total dari sistem yang terisolasi tidak berubah seiring waktu) dari sudut pandang pengamat mana pun.
• Pengamat yang berbeda bergerak relatif satu sama lain akan mengevaluasi nilai-nilai energi dan momentum sistem secara berbeda!
• Jumlah massa benda yang membentuk sistem tidak disimpan, dapat berubah.
• Tetapi semua pengamat akan setuju dengan massa objek.

Dua fakta lagi dan dua kesimpulan harus ditambahkan ke daftar ini:

Massa sistem fisik benda tidak sama dengan jumlah massa benda yang membentuk sistem ini.

Alih-alih, massa sistem fisik, yang disetujui semua pengamat, ditentukan oleh energi dan momentumnya, dan memenuhi versi persamaannya No. 1:

$$ $$(E_{system})^2 = (p_{system} c)^2 + (m_{system} c^2)^2 \qquad ( №1')$$

Ternyata hukum konservasi tambahan tidak diperlukan, dan bahwa meskipun jumlah massa benda yang membentuk sistem tidak terlindungi, massa sistem dipertahankan, karena terhubung melalui persamaan No. 1 'ke energi dan momentum sistem yang disimpan.

Massa sistem objek adalah satu-satunya item dalam daftar kami yang secara simultan dipertahankan dan tidak dapat diperdebatkan oleh pengamat.

Anda hanya perlu mengingat bahwa massa sistem benda bukan jumlah massa benda yang membentuk sistem, tetapi apa yang diberikan oleh persamaan No. 1 '.

Daripada mencoba menjelaskannya, lihat saja cara kerjanya. Contoh nyata bernilai ribuan kata. Mari kita ambil sebagai contoh dari sistem hal yang paling modis, yaitu partikel Higgs (memiliki massa 126 GeV / s ² ), dan lihat bagaimana berbagai pernyataan yang dibuat di atas bekerja ketika meluruh menjadi dua foton.

Satu partikel Higgs, dua foton dan tiga pengamat

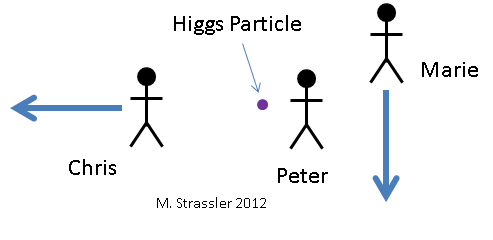Fig. 6. Tiga pengamat melihat partikel Higgs. Sehubungan dengan dia, Petya (Peter) tidak bergerak, Masha (Marie) bergerak ke bawah, dan Kostya (Chris) bergerak ke kiri.

Mari kita lihat bagaimana partikel Higgs meluruh menjadi dua foton, dari sudut pandang tiga pengamat yang berbeda. Mereka ditunjukkan dalam gambar. 6 bersama dengan partikel Higgs yang mereka lihat. Tentu saja, mereka tidak dapat melihatnya melalui mata, karena dia ada terlalu sedikit waktu dan dia terlalu kecil. Mereka perlu menggunakan beberapa jenis peralatan ilmiah. Bagi Petit, partikel Higgs tidak bergerak. Masha bergerak ke bawah relatif terhadap Petit. Kostya bergerak ke kiri relatif ke Petit. Jadi, untuk Masha, partikel Higgs bergerak ke atas, dan untuk Bone - ke kanan. Tiga pengamat melihat bagaimana sebuah partikel meluruh sesuai dengan gambar. 7. Petya melihat bahwa Higgs meluruh menjadi dua foton dengan energi yang sama, salah satunya naik dan yang lain turun. Masha melihat bahwa Higgs meluruh menjadi dua foton energi yang berbeda, dan bahwa energi yang bergerak ke atas memiliki lebih banyak energi daripada yang bergerak ke bawah.Kostya melihat Higgs membusuk menjadi dua foton menuju ke atas dan ke kanan. Mari kita hitung energi dan momentum apa yang ditugaskan pada Higgs dan dua foton oleh pengamat, dan bagaimana masing-masing dari mereka akan sampai pada kesimpulan bahwa energi dan momentum dilestarikan selama peluruhan.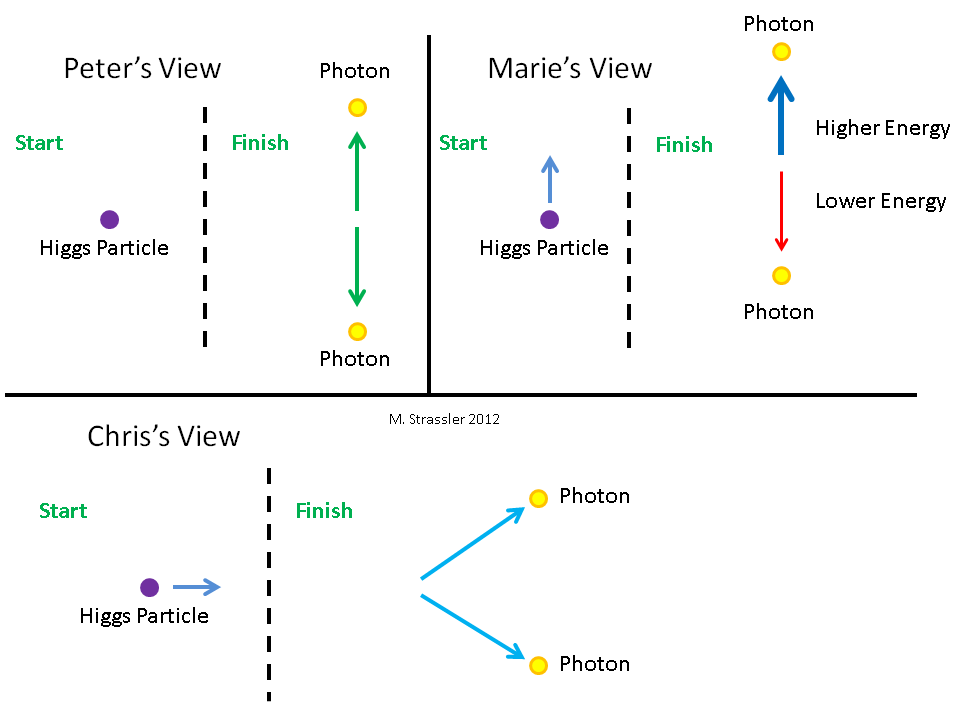

Peluruhan partikel Higgs

Pertama, kami menganalisis partikel Higgs dari sudut pandang Petit. Petya melihat (menggunakan alat pengukur) pada partikel Higgs, dan apa yang dia lihat? (Aku akan mengacaukan segala sesuatu yang dilihat Petya, dan kemudian kita membandingkannya dengan pengamatan Masha dan Kostya). Higgs tidak bergerak, begitu momentumnya$$$\overline{p_0}$sama dengan nol, dan menurut persamaan No. 1 dia, dengan massanya m = 126 GeV / c ^2, energi akan menjadi$$$\overline{E_0} = m c^2 = 126$

Sekarang, menurut konservasi energi dan momentum, sistem yang terdiri dari partikel Higgs akan menghemat semua energi dan momentum setelah peluruhan. Dan ini akan terjadi sampai tidak ada kekuatan eksternal yang mempengaruhi Higgs. Anda mungkin bertanya apakah kita perlu khawatir tentang gravitasi, karena gravitasi akan menjadi pengaruh eksternal yang dapat mengubah momentum. Jawaban saya adalah bahwa dalam waktu singkat ketika Higgs meluruh, efek gravitasi akan sangat kecil sehingga jika saya katakan seberapa kecilnya, Anda akan terkikik. Lupakan itu.

Jadi, ketika Higgs meluruh, energi partikel yang membentuk residunya harus mencapai 126 GeV, dan momentum partikel (mengingat bahwa momentum tidak hanya kuantitas, tetapi juga arah - vektor) akan berjumlah nol.

Dua foton tak bermassa ke mana Higgs meluruh dapat menyebar ke segala arah, tetapi untuk menyederhanakan contoh, bayangkan bahwa mereka tersebar secara vertikal - satu ke atas dan yang lain, memantul ke bawah, ke bawah. (Beberapa saat kemudian kita akan membahas mengapa mereka harus terbang berlawanan arah).

Apa momentum yang dimiliki foton? Sederhana saja. Pertama, total momentum sistem - jumlah momen dari dua foton - harus nol, karena Higgs memiliki momentum nol sebelum peluruhan (dari sudut pandang Peter). Sekarang masing-masing foton memiliki dorongan dari besarnya dan arah tertentu. Secara total, mereka dapat memberikan nol hanya dalam satu cara - jika besarnya sama dan berlawanan arah. Jika satu naik, yang lain harus turun, dan ukurannya harus sama.


Fig. 8: apa yang dilihat Petya

. Kedua, energi total sistem adalah jumlah energi dari dua foton. Ini karena tidak ada energi interaksi di antara mereka (kecuali untuk gaya tarik gravitasi yang sangat kecil, yang dapat Anda lupakan). Tentu saja, karena mereka tidak memiliki massa, maka semua energi mereka berada dalam energi gerak. Selain itu, dalam kasus untuk partikel tanpa massa, persamaan No. 1 menunjukkan bahwa E = pc, di mana p adalah momentum. Karena itu, dua foton dengan momenta yang sama harus memiliki energi yang sama. Dan karena dua energi ini seharusnya menambah energi partikel Higgs, energi setiap foton harus sama dengan setengah energi partikel Higgs.

$$ $$\overline E_1 = \overline E_2 = 1/2 (126 ) = 63$$

Dan karena untuk partikel tanpa massa p = E / c, maka

$$ $$\overline p_1 = 63 /c \uparrow \\ \overline p_2 = 63 /c \downarrow$$

Dan itu ditampilkan dalam gambar. 8.

Energi dan momentum dilestarikan, tetapi massa tidak, karena foton tidak memiliki massa, dan Higgs memilikinya. Bagaimana dengan massa sistem? Berapa massa sistem dua foton? Bukan nol. Jelas siapa dia. Dengan cara yang sama seperti untuk Higgs sendiri (dari mana seluruh sistem awalnya disusun), sistem dua foton memiliki energi dan momentum yang sama seperti yang dimiliki Higgs:

$$ $$E_{system} = \overline E_1 + \overline E_2 = 63 + 63 = 126 \\ p_{system} = \overline p_1 \uparrow + \overline p_2 \downarrow = 63 /c \uparrow + 63 /c \downarrow = 0$$

Dan karena untuk Petit $$$p_{system} = 0$ ,

$$ $$m_{system} = E_{system} / c^2 = 126 /c^2$$

Itu adalah massa Higgs. Massa sistem tidak berubah selama pembusukan, seperti yang diharapkan.

Pengamat untuk siapa Higgs bergerak

Masha bergerak ke bawah sehubungan dengan Peta, jadi dari sudut pandangnya, Petya dan Higgs naik. Misalkan Higgs bergerak pada kecepatan v = 0,8 detik, yaitu 4/5 kecepatan cahaya relatif terhadap itu. Tidak seperti Petya, dari sudut pandang Masha, Higgs memiliki momentum non-nol, dan momentum foton berbeda dalam besarnya, tetapi masih multidirectional - akibatnya jumlah momen mereka akan menjadi nol.


Fig. 9: bagaimana Masha melihat peluruhan partikel Higgs

Bagaimana menghitung momentum dan energi apa yang dimiliki Higgs dan dua foton yang dimilikinya, dari sudut pandang Masha? Untuk melakukan ini, kita memerlukan satu set persamaan Einstein sederhana. Misalkan, dari sudut pandang pengamat tertentu, objek memiliki momentum p dan energi E. Kemudian, dari sudut pandang pengamat lain bergerak dengan kecepatan v ke arah objek (atau melawannya), momentum dan energi objek akan dinyatakan sebagai berikut:

$$ $$p = γ (\overline p+ v \overline E/c^2) \qquad ( №3) \\ E = γ (\overline E + v \overline p) \qquad ( №4)$$

Di mana γ memenuhi persamaan Pythagoras lainnya:

$$ $$1 = v^2/c^2 + 1/γ^2 \qquad ( №5)$$

menurut Einstein. Ini memungkinkan kita untuk melakukan transformasi antara apa yang dilihat Petya dan apa yang dilihat Masha (atau pengamat lain bergerak dengan kecepatan v). Apa yang kami temukan ditunjukkan pada Gambar. 9.

Untuk membandingkan pengamatan Masha dengan Petya, kita perlu v dan γ. Saya berpendapat bahwa jika v = 4/5 c, maka γ = 5/3.

Mari kita periksa menggunakan persamaan No. 5: 1 = (4/5) 2 + (3/5) 2 = 16/25 + 9/25 = 25/25

Petya mengatakan bahwa di Higgs$$$p_0=0, E_0=126$ .Bagaimana dengan Masha? Dia mengatakan bahwa:

$$ $$p_0 = γ v \overline E_0 = (5/3) (4/5) \overline E_0 = 168 /c \uparrow \\ E_0 = γ \overline E_0 = (5/3) \overline E_0 = 210$$

Petya mengklaim bahwa dua foton $$$\overline E_1 = \overline E_2 = 63$, dan untuk masing-masing E = p c. Sekarang kita dapat menghitung apa yang dilihat Masha menggunakan persamaan No. 4 dan No. 4.

$$ $$E_1= γ (1+v) \overline E_1 = 189 , p_1 = E_1/c \uparrow$$

$$ $$E_2= γ (1-v) \overline E_2= 21 , p_2 =E_2/c \downarrow$$

Itu berhasil! Energi juga dilestarikan dari sudut pandang Mary, untuk

$$ $$E_0 = 210 \\ E_1 + E_2 = (189 + 21) = 210$$

Impuls juga disimpan:

$$ $$p_0 = 168 /c \uparrow \\ p_1 + p_2 = 189 /c \uparrow + 21 /c \downarrow = (189 – 21) /c \uparrow = 168 /c \uparrow$$

Massa sistem bertepatan dengan massa Higgs sebelum dan sesudah pembusukan, karena sebelum dan sesudah pembusukan

$$ $$E_system = 210 \\ p_system = 168 /c \uparrow$$

Yang, menurut persamaan No. 1 ', mengembalikan massa sistem $$$126 /c^2$ seperti dengan Petit, karena

$$ $$210^2 = 168^2 + 126^2$$

Pengamat, dari sudut pandang mana Higgs bergerak ke kanan

Apa yang kita miliki dengan Tulang? Kostya bergerak ke kiri relatif terhadap Petya, misalnya, pada kecepatan v = 4/5 s, sehingga Higgs (dan Petya) bergerak ke kanan sehubungan dengan Kostya pada kecepatan v = 4/5 dtk. Perhitungan yang sama yang kami lakukan untuk Masha menunjukkan energi Higgs$$$E_0 = 210 GeV dan p_0 = 168 GeV$ tetapi, tidak seperti Masha, untuk siapa Higgs bergerak ke atas, untuk Kostya, dorongan Higgs diarahkan ke kanan. Ini ditunjukkan dalam gambar. 10.


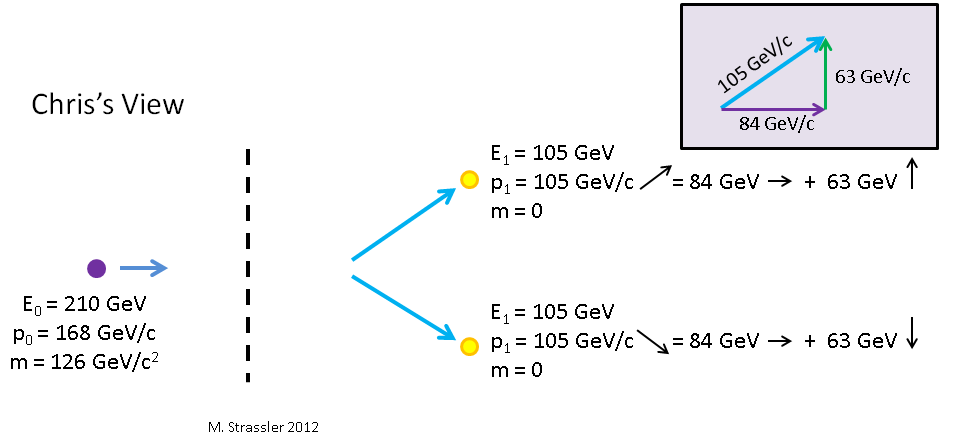
Fig. 10

Higgs meluruh menjadi dua foton. Jika dari sudut pandang Petya, foton bergerak ke atas dan ke bawah, maka untuk Kostya, yang mengawasi Higgs dan Petya bergerak ke kanan, salah satu foton bergerak ke atas ke kanan dan yang lain bergerak ke bawah ke kanan. Impuls dan energi apa yang akan mereka miliki?

Melalui persamaan No. 4 dan No. 5 kita tidak tahu ini, karena mereka dimaksudkan untuk kasus ketika partikel dan pengamat bergerak ke arah yang sama. Untuk kasus kami, persamaannya adalah sebagai berikut:

$$ $$\ updownarrow p = \ updownarrow \ overline p \\ \ leftrightarrow p = γ ([\ leftrightarrow \ overline p] + v \ overline E / c ^ 2) \\ E = γ (\ overline E + v [\ leftrightarrow \ overline p])$$

Persamaan ini akan lebih sederhana daripada yang terlihat, karena dari sudut pandang Petit, p tidak memiliki komponen yang bergerak dari kiri ke kanan, dan seluruh pulsa naik atau turun. Jadi Kostya mengamati nilai-nilai berikut untuk Higgs:

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_0 = 0 \\ \ leftrightarrow p_0 = γ v \ overline {E_0} / c ^ 2 = (5/3) (4/5) 126 GeV / c = 168 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 126 GeV = 210 GeV$$

Dan foton naik

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_1 = 63 GeV / c \ uparrow \\ \ leftrightarrow p_0 = γ v \ overline {E_1} = (5/3) (4/5) 63 GeV / c = 84 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 63 GeV = 105 GeV$$

Untuk foton kedua, rumusnya sama, hanya komponen vertikalnya yang diarahkan ke bawah. Perhatikan bahwa untuk kedua foton E = pc, sesuai dengan teorema Pythagoras untuk ukuran p untuk masing-masing pulsa, menurut inset pada Gambar. 10

$$ $$p_1 ^ 2 = (\ uparrow p_1) ^ 2 + (\ rightarrow p_1) ^ 2 \\ atau \\ (105 GeV / c) ^ 2 = (63 GeV / c) ^ 2 + (84 GeV / c) ^ 2$$

Dan lagi, Kostya mengamati nilai-nilai energi dan momentum lainnya, dibandingkan dengan Petya dan Masha. Namun bagi Kostya, energi dan momentum masih dilestarikan. Kostya juga mengamati bahwa massa sistem dengan dua foton bertepatan dengan massa Higgs. Mengapa Bagian vertikal total dari momentum sistem adalah nol, dihancurkan bersama. Bagian horisontal dari pulsa sistem adalah 168 GeV / s. Energi total sistem adalah 210 GeV. Ini sama dengan yang diamati Masha, kecuali bahwa momentum sistemnya naik, dan tidak ke kanan. Tetapi arah pulsa tidak mempengaruhi persamaan No. 1 '. Hanya besarnya yang berperan di sana. Jadi, seperti Masha, Kostya melihat bahwa massa sistem dua proton adalah $$$126 GeV / c ^ 2$ sama dengan massa partikel Higgs primer.

Ringkasan

Jadi kita melihat apa yang diamati oleh tiga pengamat berbeda. Pengamatan mereka:

• bervariasi tentang apa energi dan momentum Higgs,
• bervariasi dalam hal energi dan momentum kedua foton,
• menyetujui konservasi energi dan momentum selama peluruhan,
• oleh karena itu, mereka setuju bahwa massa sistem dipertahankan,
• setuju bahwa massa sistem adalah 126 GeV / c ² ,
• dan terlebih lagi, jumlah massa objek sistem tidak dipertahankan, tetapi menurun dari 126 GeV / c ² menjadi nol.

Dan ini bukan kebetulan. Einstein dari percobaan sebelumnya tahu bahwa energi dan momentum dilestarikan, jadi dia mencari dan menemukan persamaan yang melestarikan fitur dunia ini. Juga dalam prosesnya, ia menemukan bahwa massa sistem harus memenuhi persamaan No. 1 '.

Bonus: bagaimana ini digunakan untuk mencari partikel Higgs

Ilmuwan:

• mengamati tabrakan proton, sebagai hasil dari lahirnya dua foton;
• menghitung massa sistem dua foton (dalam jargon teknis ini disebut massa invarian sepasang foton).

Ketika, sebagai hasil percobaan, sebuah partikel Higgs meluruh menjadi dua foton, maka tidak peduli apa arah dan kecepatan partikel bergerak sehubungan dengan laboratorium, sistem dua foton yang meluruhinya akan selalu memiliki massa yang sama dengan massa. Partikel Higgs yang menghasilkannya! Oleh karena itu, tidak seperti proses acak, yang menghasilkan sistem dua foton massa acak, partikel Higgs akan selalu menghasilkan sistem dua foton dari massa yang sama. Oleh karena itu, jika partikel Higgs muncul dalam hasil percobaan, dan jika mereka kadang membusuk menjadi dua foton, maka kita akan melihat puncak dari peluruhan Higgs yang naik di atas latar belakang yang halus dari proses acak lainnya. Dan itu terjadi dalam percobaan di LHC!