Matematika memberi kita gambaran akurat tentang jawaban yang hampir pasti.

Menggunakan kertas tebal dan selotip transparan, Craig Kaplan mengumpulkan objek bulat indah yang menyerupai kreasi
Buckminster Fuller atau jenis bola sepak baru yang trendi. Ini terdiri dari empat dodecagons biasa (12-gon dengan sudut dan sisi yang sama) dan 12 decagons (10-sisi polyhedra) dengan 28 bukaan kecil dalam bentuk segitiga sama sisi. Hanya ada satu masalah - angka ini tidak bisa ada. Seperangkat poligon semacam itu tidak bertepatan dengan simpul, dan angka tersebut tidak menutup.
Model Kaplan hanya berfungsi karena ketika Anda merakitnya dari kertas, Anda memiliki sedikit kebebasan bermanuver. Sisi dapat menekuk hampir tanpa terasa. "Margin kesalahan yang timbul dari bekerja di dunia nyata dengan kertas berarti bahwa hal-hal yang seharusnya tidak mungkin benar-benar diperoleh," kata Kaplan, seorang ilmuwan komputer di University of Waterloo di Kanada.

Ini adalah contoh baru dari kelas objek matematika yang tidak terduga yang ditemukan oleh ahli matematika Amerika Norman Johnson pada 1960-an. Johnson mengerjakan penyelesaian proyek yang dimulai lebih dari 2000 tahun yang lalu oleh Plato - ia membuat katalog bentuk geometris yang ideal. Dari variasi tak terbatas dari angka tiga dimensi, hanya
lima yang dapat dibuat dari poligon beraturan yang sama: tetrahedron, octahedron, hexahedron, icosahedron, dodecahedron. Jika Anda mencampur poligon reguler yang berbeda, Anda dapat membuat 13 bentuk lagi di mana semua poligon bertemu dengan simpul -
benda Archimedean - serta prisma (dua poligon identik yang dihubungkan oleh kotak) dan "antiprisma" (dua poligon identik yang dihubungkan oleh segitiga sama sisi).
Pada tahun 1966, Johnson, ketika bekerja di University of Michigan, menemukan 92 badan lagi yang hanya terdiri dari poligon biasa, yang sekarang [di AS] disebut
badan Johnson . Dan ini menghabiskan semua kemungkinan, yang dibuktikan beberapa tahun kemudian oleh matematikawan Rusia
Viktor Abramovich Zalgaller , yang kemudian bekerja di Universitas Negeri Leningrad. Tidak mungkin membuat bentuk tertutup lain dari poligon biasa.
Tetapi selama inventarisasi polyhedra, Johnson memperhatikan sesuatu yang aneh. Dia menemukan formulirnya, menyusun model mereka dari karton dan karet gelang. Karena ada beberapa kemungkinan polyhedron, ia berharap bentuk-bentuk baru akan muncul lebih cepat. Jika Anda mulai membuat wajah bersama, maka angka tersebut harus bersamaan. Tetapi ini tidak terjadi. "Ketika merakit setumpuk poligon, tidak selalu jelas apakah saya telah membuat bentuk yang valid," kenang Johnson.
Mungkin terlihat bahwa model telah berkumpul, tetapi "jika Anda membuat perhitungan, ternyata ini tidak sepenuhnya benar," katanya. Setelah diperiksa dengan teliti, ternyata kotak yang kelihatannya bukan kotak, atau sisi-sisinya tidak rata. Mungkin saja sedikit memangkas wajah, dan mereka akan pas dengan sempurna, tetapi kemudian mereka tidak lagi menjadi poligon biasa.
Berniat menghitung semua angka ideal, Johnson tidak mementingkan "hit dekat" tersebut. "Saya mengesampingkannya, dan berkonsentrasi pada yang dapat diterima," katanya. Tetapi angka-angka yang hampir ideal ini tidak hanya menarik perhatian Kaplan dan pecinta matematika lainnya, mereka menjadi bagian dari bagian yang lebih besar dari matematika yang hampir ideal.
Tidak ada definisi pasti mengenai hit "hampir akurat". Aturan ketat tidak berlaku di dunia yang toleran. Sekarang, Kaplan dipandu oleh metode perkiraan dalam mencari angka yang hampir benar: "kesalahan matematika nyata yang melekat pada gambar sebanding dengan kesalahan praktis yang timbul dari bekerja dengan bahan dunia nyata dan tangan yang tidak sempurna." Dengan kata lain, jika Anda berhasil membuat polyhedron yang tidak mungkin - jika sedekat mungkin sehingga Anda bisa melewatinya dengan yang asli - maka ini akan menjadi angka yang hampir pasti. Di cabang matematika lain, hasil yang hampir akurat sangat dekat dengan nyata sehingga mereka bisa menipu atau mengejutkan Anda - semacam lelucon matematika.
Beberapa keanehan matematika ini tidak bisa disebut lebih dari kesenangan sederhana, sementara yang lain dapat memiliki makna mendalam dalam matematika dan fisika.
Masalah kuno
mengkuadratkan lingkaran dan
menggandakan kubus jatuh ke dalam kategori solusi yang hampir benar. Mereka tampak terbuka untuk menemukan solusi yang tepat, tetapi pada akhirnya mereka ternyata tidak mungkin - seperti sosok geometris yang terlihat tertutup tetapi tidak. Beberapa desain yang digambar oleh Leonardo da Vinci dan Albrecht Durer sedikit membengkokkan sudut, memberikan pentagon hampir biasa sebagai yang asli.
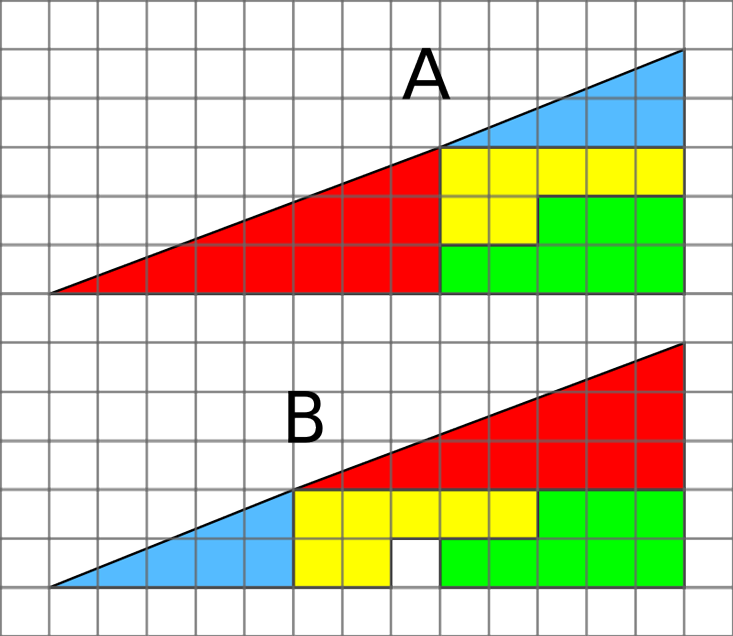
Dan ada teka-teki dengan kotak yang hilang. Dalam gambar, segitiga siku-siku dipotong menjadi empat bagian. Jika Anda mengatur ulang, ada celah di dalamnya. Dari mana asalnya? Ini juga keputusan yang hampir tepat. Tak satu pun dari segitiga itu yang benar-benar segitiga. Hipotensi mereka bengkok, dan hampir tidak mungkin untuk diperhatikan, itulah sebabnya ilusi begitu meyakinkan.
Pencocokan digital adalah salah satu keputusan paling dekat yang paling berguna dalam kehidupan sehari-hari. 2
7/12 hampir sama dengan 3/2. Untuk alasan yang sama, piano memiliki 12 kunci dalam satu oktaf dan merupakan inti dari
sistem musik Barat yang
diperlunak secara merata . Ini adalah kompromi antara dua interval musik paling penting: satu oktaf (frekuensi 2: 1) dan yang kelima (frekuensi 3: 2). Secara numerik, tidak mungkin untuk membagi satu oktaf sehingga semua perlima sempurna. Tetapi Anda bisa cukup dekat dengan ini dengan membagi oktaf menjadi 12 semitone, tujuh di antaranya akan memberi Anda frekuensi 1,498. Bagi kebanyakan orang, ini sudah cukup.
Terkadang hit yang hampir pasti terjadi dalam matematika seolah-olah menipu dirinya sendiri. Dalam episode Simpsons "Treehouse of Horror VI," khalayak yang tertarik dengan matematika memperhatikan sesuatu yang tidak biasa: persamaan 1782
12 + 1841
12 = 1922
12 . Pada pandangan pertama, tampaknya penulis menolak Fema's Great Theorem, mendalilkan bahwa persamaan x
n + y
n = z
n tidak memiliki solusi bilangan bulat untuk n> 2. Jika Anda memasukkan angka-angka ini ke dalam kalkulator saku, hasilnya akan tampak benar. Tetapi jika Anda membuat perhitungan dengan akurasi tidak tersedia untuk sebagian besar kalkulator saku, ternyata akar derajat ke-12 dari sisi kiri persamaan adalah 1921,999999955867 dan bukan 1922, dan Fermat bisa tenang. Slip mengejutkan kecil - kurang dari 10 juta bagian.
Tapi hit yang hampir akurat semacam itu bukan hanya lelucon. "Orang-orang yang lebih menggelitik saya daripada yang lain adalah kasus-kasus yang mengisyaratkan kehadiran sesuatu yang lebih signifikan," kata John Baez, seorang ahli matematika di University of California di Riverside. Ini adalah kasus kuantitas yang kadang-kadang disebut konstanta
Ramanujan . Angka
π √163 ini , sama dengan kira-kira 262 537 412 640 768 743.9999999999999925, secara mengejutkan mendekati keseluruhan. Kita tidak dapat berharap bahwa ketiga bilangan irasional ini - e, π, dan √163 - entah bagaimana akan menggabungkan dan memberi kita bilangan rasional, belum lagi keseluruhannya. Tapi ada alasan mengapa mereka sangat cocok. "Bukan hanya kebetulan bahwa kita tidak tahu," kata Baez. "Ini adalah kunci kedalaman matematika." Penjelasan persisnya agak rumit, tetapi berdasarkan fakta bahwa 163 adalah yang terbesar dari
angka Hegner . Peserta pameran yang terkait dengan angka-angka ini sangat dekat dengan bilangan bulat.
Atau ambil koneksi matematis yang dikenal sebagai "Hipotesis Moonshine Monstrous" (nonsen Moonshine). Ceritanya begini: pada tahun 1978, ahli matematika John Mackay membuat cara yang sepele, sama menariknya, pengamatan: 196 884 = 196 883 + 1. Angka pertama adalah koefisien polinomial penting,
invarian-j , dan yang kedua muncul sehubungan dengan objek matematika besar dari teori grup. disebut "
Monster ". Banyak orang akan mengangkat bahu dan melangkah lebih jauh, tetapi pengamatan ini menarik banyak ahli matematika yang memutuskan untuk mempelajarinya lebih dekat. Mereka menemukan hubungan antara dua topik yang tampaknya tidak berhubungan: teori bilangan dan simetri kelompok Monster. Koneksi ini mungkin memiliki konsekuensi yang lebih luas, belum terbuka, untuk topik lainnya. Fisikawan Edward Whitten percaya bahwa kelompok Monster dapat dikaitkan dengan gravitasi kuantum dan struktur ruang-waktu.
Matematika hampir benar hit menunjukkan baik main-main dan kekuatan dari pendekatan manusia terhadap matematika. Johnson, Kaplan dan yang lainnya membuat penemuan melalui coba-coba - mempelajari bidang tersebut sebagai ahli biologi yang mengarungi hutan untuk mencari spesies baru. Namun dalam matematika, lebih mudah untuk melakukan pencarian sistematis. Misalnya, Jim McNeill, yang tertarik pada matematika sebagai hobi dan mengumpulkan koleksi hit yang hampir benar di situsnya, dan Robert Webb, seorang programmer, menciptakan perangkat lunak untuk membuat dan mempelajari polyhedra.
Hit yang hampir akurat hidup di garis yang kabur antara matematika idealistis, keras dan perasaan merendahkan dan praktis kita. Mereka membalikkan logika perkiraan. Biasanya dunia nyata dianggap sebagai bayangan tidak sempurna dari dunia Plato. Kesempurnaan matematika yang mendasarinya hilang dalam implementasinya. Tetapi dalam kasus hit yang hampir akurat, dunia nyata adalah bayangan sempurna dari dunia yang tidak sempurna. Perkiraan adalah "perkiraan yang salah dari jawaban yang benar," kata Kaplan, dan "hit yang hampir akurat adalah representasi akurat dari jawaban yang hampir akurat."
Dengan cara ini, jawaban yang hampir akurat mengubah hubungan antara ahli matematika dan ahli fisika matematika dengan alam. "Saya berterima kasih atas ketidaksempurnaan dunia nyata, karena mereka memungkinkan saya untuk mencapai semi-ideal dengan bekerja dengan benda-benda yang pada dasarnya tidak sempurna," kata Kaplan. "Mereka memungkinkan saya untuk mengatasi keterbatasan matematika berkat keindahan dari realitas yang rusak."