Kami memahami fisika partikel: 1) bola pada pegas, versi Newtonian

1. Bola pada pegas, versi Newton
2. Bola kuantum pada pegas
3. Gelombang, tampilan klasik
4. Gelombang, persamaan gerak klasik
5. Gelombang kuantum
6. Fields
7. Partikel adalah kuanta
8. Bagaimana partikel berinteraksi dengan bidang

Untuk memahami secara umum dasar-dasar fisika partikel - dan inilah pemahaman kita saat ini atas sebagian besar fenomena alam semesta - tidaklah begitu sulit. Akan lebih mudah bagi Anda jika Anda menghadiri sekolah fisika dan matematika atau menyelesaikan tahun pertama kuliah. Tetapi jika Anda berurusan dengan aljabar, trigonometri dan (mungkin, tetapi tidak harus) dasar-dasar diferensiasi dan integrasi, maka Anda dapat memahami cara kerja bidang dan bagaimana partikel muncul. Anda hanya perlu mengambil kata saya untuk itu sekali, mengenai satu aspek mekanika kuantum. Dalam hal ini, saya tidak akan memberikan rumus matematika, tetapi hanya menunjukkan kepada Anda jawaban yang sudah jadi. Tetapi setelah Anda menerima aspek ini, segalanya akan menjadi jelas.


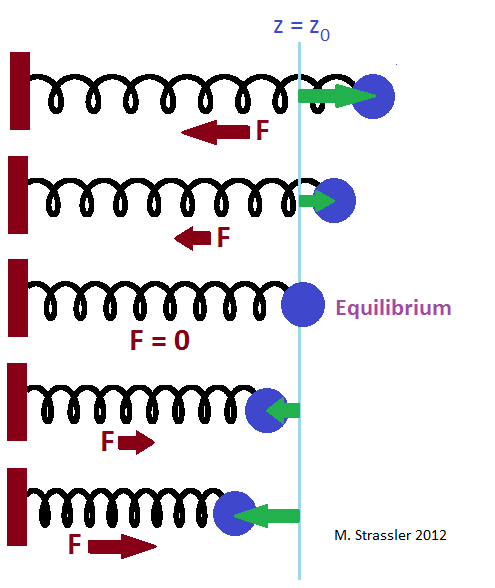Fig. 1

Untuk memahami fisika partikel, dari fisika sekolah Anda perlu mengingat satu hal - cara kerja pegas. Faktanya, segala sesuatu yang memantul, bergetar, berdering, bergetar, berayun bolak-balik, adalah contoh pegas.

Bayangkan kita menempatkan bola di ujung pegas. Pergerakan pegas dan persamaan yang menggambarkannya sederhana. Untuk memulainya, kita mengingat dasar-dasar perilaku pegas, lalu kita mempelajari perilaku osilasi bola. Dan akhirnya, untuk pikiran yang paling bertanya, kita akan mempertimbangkan persamaan yang mengarah ke gerakan semacam ini.

Osilator harmonik (alias bola pada pegas)

Bola pada pegas memiliki posisi seimbang; jika Anda meletakkan bola di sana dan melepaskannya, pegas tidak akan mendorongnya ke segala arah, dan bola akan tetap tidak bergerak. Ini adalah garis biru dalam gambar. 1. Jika Anda menarik bola menjauh dari posisi keseimbangan (panah hijau), pegas akan menarik bola kembali dengan gaya F (panah merah). Semakin jauh Anda menarik bola, semakin kuat pegas menariknya kembali (setidaknya sampai Anda mematahkan pegas atau mematahkannya dengan tekanan).

Gerakan berosilasi (melompat)

Kami menyebut arah gerakan bola "arah z", dan menentukan sumbu z sehingga z = z ₀ sesuai dengan posisi keseimbangan bola pada pegas. Misalkan kita menarik bola dari posisi ini, pegang bola agar tidak bergerak, ke posisi z = z ₀ + A; kemudian, pada titik waktu t = 0, kami lepaskan. Bola akan mulai melompat di sana-sini - lihat gambar. 2. Besarnya lompatan - amplitudo osilasi - sama dengan A. Ia dapat berukuran besar atau kecil; hanya Anda yang memilih berapa banyak untuk menarik bola dari posisi setimbang. Tetapi Anda tidak mengontrol seberapa sering melompat ke sana kemari - frekuensi osilasi ν - terjadi. Ternyata sama, terlepas dari nilai A. Itu ditentukan hanya oleh sifat bola dan pegas, dan bukan oleh apa yang Anda lakukan.

Untuk tujuan ilmiah, sangat penting untuk menggambarkan pengamatan melalui rumus matematika. Posisi bola z adalah fungsi waktu t, ditulis oleh kami sebagai z (t), berbentuk:

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

Di mana, seperti biasa, cos adalah cosinus, π adalah bilangan pi dari geometri lingkaran, z ₀ adalah posisi kesetimbangan bola, dan A dan ν (nu) adalah amplitudo dan frekuensi osilasi. Fungsi cosinus adalah osilasi, oleh karena itu rumus ini menjelaskan gerakan osilasi dengan amplitudo A dan frekuensi ν. Contoh gerak osilasi bola pada pegas dengan nilai deviasi awal yang berbeda dan total amplitudo A ditunjukkan pada Gambar. 2, yang juga menunjukkan bahwa untuk bola yang diberikan pada pegas, frekuensi ν tidak tergantung pada amplitudo A.

Cetak halus: amplitudo dan frekuensi lebih besar dari nol. Jika A negatif, maka amplitudo akan –A. Bahkan, amplitudo sebenarnya | A |, yaitu, modulus besarnya.


Fig. 2

Apa yang sangat penting untuk diingat tentang amplitudo dan frekuensi bola dan pegas (dalam fisika pra-kuantum klasik):
• amplitudo A dapat dipilih apa saja;
• frekuensi ν ditentukan oleh bola dan pegas, dan untuk memilih frekuensi yang berbeda, Anda harus mengganti pegas atau bola.

Periode setiap osilasi (berapa lama waktu yang dibutuhkan bola untuk maju dan mundur tepat sekali) akan disebut T, dan periode ini hanyalah kebalikan dari frekuensi: T = 1 / ν. Jika periode adalah 5 detik, maka frekuensinya adalah sekali setiap lima detik, atau 1/5 detik (yang sering disebut 1/5 Hertz atau Hz).

Cetakan kecil lainnya: dalam sistem pegas dan bola nyata apa pun yang akan Anda temui dalam kehidupan sehari-hari, gesekan akan mengarah pada fakta bahwa A secara bertahap akan berkurang dan akhirnya mencapai nol ketika gerakan berhenti. Formula yang memperhitungkan gesekan selama pergerakan tidak jauh lebih rumit, tetapi kita tidak akan membutuhkannya. Oleh karena itu, saya selalu menganggap bahwa gesekan itu kecil, A menurun sangat lambat, dan kita bisa menggunakan rumus sederhana yang mengabaikan gesekan. Tetapi penting untuk diketahui: gesekan mengurangi A, tetapi, kecuali itu sangat kuat, tidak mempengaruhi ν dan T! Frekuensi osilasi tetap sama bahkan dengan penurunan amplitudo. Karena itu, perhatikan bahwa senar gitar menghasilkan setelah Anda menariknya tidak berubah, bahkan ketika suara yang dihasilkan secara bertahap memudar.

Satu hal lagi: ada formula indah untuk energi yang disimpan dalam pegas berosilasi. Ini sebanding dengan kuadrat dari amplitudo dan kuadrat dari frekuensi:

$$

$$E = 2 \ pi ^ 2 \ nu ^ 2 A ^ 2 M$$

Sebagian, ini adalah energi gerak bola (kinetik), dan sebagian, energi interaksi (potensial) yang disimpan di pegas, dan ketika bola bergerak bolak-balik, fraksi energi ini dalam total energi terus berubah. Tetapi energi total E tetap konstan.

Cetak kecil: masih ada energi dari massa bola, Mc ² , tapi kami tidak melacaknya, karena selalu ada di sana, pegas bergerak bersamanya, atau tidak.

Formula osilasi yang sama berlaku untuk hampir semua yang bergetar atau melompat hanya jika lompatan ini tidak terlalu besar. Sebuah bola menggelinding di sepanjang bagian bawah mangkuk; sebuah mobil melompat pada peredam kejut yang buruk; string bergetar biola atau gitar; bilah gambang setelah memukulnya; dll.

Persamaan gerak getaran (matematika melompat)

Sekarang mari kita ingat rumus dasar yang menjelaskan kepada kita mengapa bola di pegas berosilasi.

Seperti yang kami sebutkan di awal (Gbr. 1), bola pada pegas memiliki posisi setimbang, yang kami sebut z = z0. Misalkan pada suatu titik waktu (entah kita menarik bola, atau ragu-ragu), ia berada di posisi yang berbeda, z. Jika z> z ₀ , yaitu, jika perpindahan dari posisi kesetimbangan z - z ₀ lebih besar dari nol, maka pegas akan menciptakan gaya yang diarahkan ke arah negatif z untuk menarik bola kembali ke titik kesetimbangan. Sebaliknya, jika z <z ₀ , yaitu, perpindahan dari kesetimbangan z - z _{0 adalah} negatif, maka pegas akan menciptakan gaya yang diarahkan ke arah positif z, sekali lagi untuk menarik bola kembali ke titik kesetimbangan. Dan semakin jauh bola dari posisi keseimbangan, semakin kuat pegasnya. Gaya F yang diciptakan oleh pegas terkait dengan perpindahan bola dari kesetimbangan berdasarkan persamaan

$$

$$F = - K (z - z_0)$$

Di mana K adalah nilai positif, tergantung pada pegas tertentu, yang disebut konstanta pegas.

Perhatikan mengapa rumus ini benar:

• Jika bola berada di posisi setimbang, F = 0. Pegas tidak menciptakan gaya, dan jika bola tidak bergerak di posisi setimbang, ia akan tetap di sana.
• Jika deviasi lebih besar dari nol, gaya negatif.
• Jika deviasi negatif, gaya positif.
• Semakin besar penyimpangan, semakin besar kekuatannya.

Kemudian kita beralih ke hukum gerak kedua Newton, yang menyatakan bahwa di bawah pengaruh gaya F, bola massa M akan bergerak dengan akselerasi a, di mana F = M a. Ganti ini dalam formula dan dapatkan

$$

$$M a = - K (z - z_0)$$

atau

$$

$$a = - K / M (z - z_0)$$

Ini adalah persamaan yang hampir perlu bagi kita, yang darinya kita dapat menurunkan persamaan osilasi. Kita hanya perlu mengingat kembali hubungan antara a dan z. Untuk ini, penting untuk mengingat hubungan antara a dan kecepatan v, dan antara v dan z. Rasio ini adalah salah satu dari dua perubahan dari waktu ke waktu:
• Kecepatan adalah perubahan posisi dalam waktu, v = dz / dt
• Akselerasi adalah perubahan kecepatan dari waktu ke waktu, a = dv / dt

Tambah dan dapatkan

$$

$$a = d (dz / dt) / dt = d ^ 2z / dt ^ 2$$

Akselerasi adalah perubahan waktu dari perubahan posisi dari waktu ke waktu.

Kita dapat menulis ulang persamaan gerak kita

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0) \ quad (*)$$

Di mana z adalah notasi singkat untuk z (t). Dan sekarang kita dapat memverifikasi bahwa gerakan getaran z (t) = z ₀ + A cos [2 π ν t] akan menjadi solusi untuk persamaan gerak ini. Pertama-tama kita perlu menghitung kecepatan partikel sebagai perubahan posisinya dalam waktu:

$$

$$d / dt (z_0 + A cos [2 \ pi \ nu t]) = - (2 \ pi \ nu) Dosa [2 \ pi \ nu t]$$

(dz ₀ / dt = 0, karena posisi kesetimbangan z ₀ tidak berubah dengan waktu, dan d / dt (cos wt) = -w sin wt); dan kemudian kita menghitung percepatan partikel sebagai perubahan kecepatannya dari waktu ke waktu:

$$

$$d / dt [- (2 \ pi \ nu t)] = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t]$$

(sejak d / dt (sin wt) = w cos wt). Hasilnya

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t] = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

Di mana pada langkah terakhir saya menggunakan rumus z (t) = z ₀ + A cos [2 π ν t] untuk gerak osilasi. Persamaan terakhir sama dengan persamaan gerak kita [ $$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$], mengingat bahwa (2 π ν) ² = K / M, jika frekuensi osilasi

$$

$$ν = \ frac {\ sqrt {K / M}} {2 \ pi}$$

Dan kami, pada kenyataannya, menemukan bahwa persamaan gerak kami menyiratkan bahwa pegas akan berosilasi dengan frekuensi yang ditunjukkan, bahwa frekuensi ini tidak tergantung pada A - itu hanya tergantung pada sifat-sifat pegas (K) dan bola (M) - dan bahwa terlepas dari dari kuantitas A untuk persamaan ada solusinya. Oleh karena itu, kita dapat memilih A, tergantung pada seberapa jauh kita menarik bola dari posisi setimbang sebelum melepaskannya.

Resonansi

Resonansi adalah salah satu fenomena alam yang paling penting, baik dalam kehidupan sehari-hari, di mana ia berperan dalam banyak aspek teknologi dan musik, dan dalam proses dasar dunia fisik, terutama dalam fisika partikel.

Pertama, ingat bagaimana ayunan itu bekerja. Ayunan, seperti bola pada pegas, atau pendulum apa pun, adalah osilator - ia berayun bolak-balik dengan frekuensi tertentu, yang tidak bergantung pada amplitudo ayunan. Dalam kasus ayunan, pernyataan ini tetap benar sampai amplitudo sangat besar. Anda mungkin tahu dari pengalaman bahwa untuk mengayunkan anak lebih tinggi, Anda harus mendorong ayunan ke depan satu kali per siklus sehingga amplitudo ayunan terus meningkat. Jika Anda mendorong ayunan ke depan beberapa kali per siklus, atau sekali setiap dua setengah siklus, kadang-kadang Anda akan meningkatkan amplitudo ayunan, dan kadang-kadang menguranginya. Jelas, ada sesuatu yang istimewa tentang menyelaraskan frekuensi dengan mana Anda mendorong ayunan dengan frekuensi alami ayunan itu sendiri.

Demikian pula, jika anak itu sendiri tahu cara mengayunkan ayunan, ia tahu bahwa ia perlu mengayunkan kakinya pada saat yang sama dengan frekuensi alami ayunan untuk meningkatkan amplitudo ayunan. Ayunkan dengan cara yang berbeda, dan amplitudo tidak akan tumbuh.



Anda dapat melacak bagaimana ini terjadi dengan bola di pegas. Lihat gambarnya. Di sebelah kiri adalah bola yang berosilasi ke sana kemari di sekitar posisi keseimbangan. Dia ragu-ragu, tanpa guncangan dari luar. Berosilasi dengan frekuensi alami pegas ν. Frekuensi adalah √ K / M, di mana K adalah gaya pegas, M adalah massa bola.

Di sebelah kanan di gambar. Anda dapat melihat apa yang terjadi pada bola hitam, bola, massa yang sama dengan yang pertama, pada pegas yang sama, yang didorong dengan gaya F (besarnya dan arahnya ditunjukkan oleh panah merah), yang berosilasi dengan frekuensi ν _F berbeda dengan ν. Bola hitam berperilaku seperti ayunan yang terlalu jarang mendorong; mereka akan bergerak dalam pola yang kompleks dan tidak akan naik tinggi. Dalam gbr. dapat dilihat bahwa bola tidak terombang-ambing dengan sangat halus, dan amplitudo dari osilasi kecil. Anda dapat melihat bagaimana ia "mencoba" berosilasi dengan frekuensi alami, meskipun gerakan umumnya diulang dengan frekuensi ν _F.

Kemudian gambar menunjukkan kasus di mana gaya berosilasi dengan frekuensi ν _F , yang jauh lebih tinggi daripada frekuensi ν. Sekali lagi, Anda dapat melihat bagaimana ia "mencoba" berosilasi dengan frekuensi alami, tetapi ia tidak berhasil melakukan ini dengan amplitudo besar, karena gaya berosilasi cepat dapat mendorongnya ke dalam atau melawan gerakan, menambah atau mengurangi amplitudo .

Dan pada akhirnya, kasing ditunjukkan ketika gaya berosilasi dengan frekuensi alami pegas, ν _F = ν. Bola bereaksi sangat berbeda: amplitudo osilasi terus tumbuh, dan bola hitam berosilasi semudah dan semulus bola putih di sebelah kiri, tetapi dengan peningkatan amplitudo. Ini adalah resonansi.

Akibatnya: jika ν _F berbeda dari ν - jika gaya tidak memungkinkan bola masuk ke resonansi - ia akan bergerak, tetapi dengan enggan, dan gerakannya akan sangat berbeda dari alam, dari osilasi sederhana dengan frekuensi ν. Sebaliknya, jika frekuensi gaya sesuai dengan yang alami - jika gaya memasukkan bola ke resonansi - maka gaya mendorong bola jauh lebih efisien, dan gerakan yang dihasilkan lebih mengesankan. Kami tahu ini secara intuitif; mendorong ayunan dengan frekuensi alami, anak (atau orang tua) mengayunkan ayunan lebih tinggi dan lebih tinggi.

Di antara aspek-aspek penting dari resonansi dalam fisika partikel adalah fakta bahwa dalam keadaan tertentu, partikel dapat dihasilkan karena mekanisme yang sangat mirip: setelah tabrakan dua partikel, gaya diperoleh dengan frekuensi yang persis sama seperti yang diperlukan untuk membuat partikel ketiga.

Lain kali: bola kuantum pada pegas

Ini adalah perilaku bola pada pegas dalam fisika klasik, pra-kuantum. Mekanika kuantum mengubah banyak konsep , tetapi yang paling penting adalah ini: kita masih bisa memilih A, tetapi A tidak bisa dalam ukuran berapa pun. Hanya dapat mengambil nilai tertentu yang proporsional dengan akar kuadrat dari bilangan bulat.