Kami memahami fisika partikel: 3) gelombang, bentuk klasik

1. Bola pada pegas, versi Newton
2. Bola kuantum pada pegas
3. Gelombang, tampilan klasik
4. Gelombang, persamaan gerak klasik
5. Gelombang kuantum
6. Fields
7. Partikel adalah kuanta
8. Bagaimana partikel berinteraksi dengan bidang

Setelah berurusan dengan persamaan untuk osilasi - menggambarkan hampir semua yang melompat, bergetar, bergulung-guling, seperti bola pada pegas - kita dapat beralih ke fenomena alam yang sama-sama umum, yaitu gelombang. Ombak ada di mana-mana: suara dan cahaya, gempa bumi, riak di permukaan kolam, dll.


Fig. 1

Tetapi sebelum itu, saya memperingatkan Anda bahwa istilah "gelombang" dapat menyesatkan, karena dalam fisika itu tidak berarti sama dengan dalam bahasa Inggris. Dalam fisika, itu tidak berarti apa yang biasanya kita sebut gelombang di tepi lautan - satu lambang dan satu lekukan. Dalam fisika, gelombang adalah urutan gelombang, beberapa punggung bukit dan palung yang bergerak bersama dalam arah yang sama. Dalam gelombang dengan bentuk paling sederhana, semua punggung bukit memiliki ketinggian yang sama dan berjarak satu jarak dari satu sama lain. Kami akan mempertimbangkan kasus seperti itu.

Gelombang adalah fenomena luar biasa, jika Anda memikirkannya. Bayangkan Anda dan teman Anda mengambil tali panjang dan menariknya erat-erat ke dalam ruangan (Gbr. 2). Kemudian bayangkan teman Anda mengobrol beberapa kali dengan satu ujung tali (hijau). Gelombang akan muncul di ujung tali dan akan melewati ruangan ke ujung tali (merah).


Fig. 2

Ini luar biasa. Maksud saya - ini benar-benar luar biasa, kuat dan kritis untuk segala sesuatu di alam semesta kita, termasuk Anda secara pribadi. Lihat apa yang terjadi. Tidak ada benda fisik yang bergerak dari kiri ke kanan - sebelum teman Anda mulai menggerakkan ujung talinya, ia direntangkan melintasi ruangan, dan pada akhirnya, setelah ujung talinya berhenti bergetar dan ombaknya menghilang, talinya akan tetap terentang melewati keseluruhan ruangan, seperti itu. Dan lagi! Energi dan informasi bergerak di sekitar ruangan. Gelombang di jalan membawa energi yang dihabiskan oleh teman Anda pada getaran tali - dan membawa informasi bentuknya tentang berapa kali dan seberapa cepat ia menariknya - kepada Anda, di mana itu membuat tangan Anda bergetar. Dan dalam hal ini, dia bahkan akan menjabat tangan Anda beberapa kali dan dalam urutan itu. Wow! Tidak ada satu pun benda fisik bergerak melalui ruangan, dan energi dan informasi bergerak.

Atau tunggu. Tetapi bukankah kita seharusnya menganggap gelombang sebagai objek fisik? Fisik seperti tali itu sendiri?

Mengingat pertanyaan terdalam ini, mari kita beralih ke sejumlah kecil rumus matematika yang diperlukan untuk menggambarkan penampilan dan perilaku gelombang, dan kemudian menggunakan sedikit lebih banyak matematika untuk menuliskan persamaan yang solusinya adalah gelombang. Ini mirip dengan apa yang kami lakukan untuk bola musim semi klasik.

Formula untuk gelombang tak terbatas pada titik waktu tertentu

Seri artikel ini segera setelah bola di pegas menuju ke gelombang karena gelombang adalah semacam osilator ganda. Ini berfluktuasi baik dalam waktu maupun ruang. Kami akan menetapkan waktu dengan huruf "t", dan ruang dengan "x".

Perhatikan ara. 3. Ini menggambarkan gelombang memanjang di kedua arah pada jarak yang besar, di mana banyak bubungan dan depresi cocok. Ini berbeda dari gelombang dalam gambar. 2, yang hanya memiliki beberapa punggung bukit dan depresi. Tetapi perbedaan ini tidak relevan - pada Gambar. 2 Saya perlu mengilustrasikan apa bentuk gelombang yang sebenarnya tidak penting; Sekarang kita akan berkonsentrasi pada rumus matematika untuk gelombang, dan itu jauh lebih mudah dilakukan jika gelombang memiliki banyak punggungan dan depresi dengan ukuran yang sama. Juga, kasus ini akan terbukti sangat berguna untuk memahami bagaimana mekanika kuantum mempengaruhi perilaku gelombang.



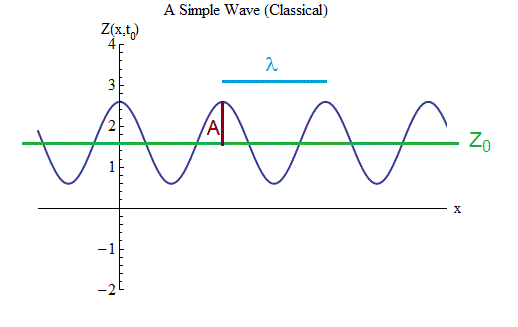
Fig. 3

Pertama, kita perlu menentukan notasi dan menuliskan formula yang menggambarkan gerakan dan bentuk gelombang pada Gambar. 3, seperti yang kami lakukan untuk bola di musim semi.

Grafik menunjukkan besarnya gelombang Z sebagai fungsi ruang dalam periode waktu t = t ₀ - kami mencatat ini sebagai Z (x, t ₀ ). Melacak gelombang di ruang angkasa, kita melihat bahwa itu berosilasi maju dan mundur, dan Z secara berkala meningkat dan menurun. Setiap saat, gelombang berosilasi di ruang angkasa.

Perhatikan bahwa Z tidak harus terkait dengan jarak fisik. Ini bisa menjadi tinggi tali, seperti pada gambar. 2, atau bisa juga sesuatu yang sama sekali berbeda, misalnya, suhu udara pada titik tertentu dalam ruang dan waktu atau orientasi atom magnetik di tempat tertentu dari suatu magnet. Tetapi x masih mewakili jarak fisik, dan t adalah waktu.

Tembakan gelombang ini, Z (x, t ₀ ), memiliki tiga sifat menarik, dua di antaranya juga berlaku untuk bola pada pegas.

1. Ada nilai keseimbangan Z _{0 yang} terletak di tengah antara nilai Z terbesar di punggung bukit dan nilai Z terkecil dalam depresi. Sebagian besar waktu kita mempelajari gelombang yang Z ₀ = 0, karena seringkali nilai Z ₀ tidak masalah - tetapi tidak selalu.
2. Gelombang memiliki amplitudo A, nilai di mana Z berubah dari nilai keseimbangan ke bagian atas setiap bubungan atau dengan nilai yang sama ke bagian bawah setiap depresi.
3. Gelombang memiliki panjang - jarak λ antara punggungan yang berdekatan, atau, apa yang sama, antara palung tetangga, atau, yang sama, dua kali jarak antara punggungan dan palung yang berdekatan. Ini menggambarkan osilasi dalam ruang dengan cara yang sama bahwa suatu periode (sama dengan 1 / frekuensi) menggambarkan osilasi dalam waktu bola pada pegas.


Fig. 4

Yang mengingatkan kita pada formulir pada Gambar. 3? Ini terlihat seperti grafik fungsi sinus atau kosinus - lihat gambar. 4, di mana cos (w) diplot pada w. Cos (w) adalah fungsi osilasi, yang memiliki posisi kesetimbangan yang jelas pada nol, amplitudo-nya adalah 1, dan panjang gelombangnya adalah 2π. Bagaimana cara pergi dari ara. 4 ke rumus untuk gelombang pada Gambar. 3? Pertama, kita mengalikan cos (w) dengan A, sehingga amplitudo sama dengan A. Kemudian kita menambahkan Z ₀ ke seluruh rumus untuk menggesernya ke nilai kesetimbangan yang diinginkan (jika A = 0, maka tidak ada osilasi, dan semuanya berada pada titik Z = Z ₀ ). Dan akhirnya, ganti w dengan 2πx / λ, karena cos (w) memiliki ridges pada w = 0 dan w = 2 π, oleh karena itu, pada cos (2πx / λ), ridges akan memiliki pada x = 0 dan x = λ. Secara keseluruhan itu memberi kita

$$

$$Z (x, t_0) = Z_0 + A cos (2 \ pi x / \ lambda)$$

Ini adalah formula yang hampir sama yang menggambarkan pergerakan bola pada pegas waktu:

$$

$$z (t) = z_0 + A cos (2 \ pi \ nu t) = z_0 + A cos (2 \ pi t / T)$$

Di mana ν adalah frekuensi osilasi, dan T = 1 / ν adalah periode osilasi. Lihat analogi: suatu periode mengacu pada waktu sebagai panjang gelombang mengacu pada ruang.

Satu catatan lagi sebelum kita melanjutkan. Saya juga bisa menulis:

$$

$$Z (x, t_0) = Z_0 + A cos (- 2 \ pi x / \ lambda)$$

Karena cos [w] = cos [-w]. Fakta bahwa kita dapat dengan mudah mengganti minus dalam rumus bentuk gelombang akan menjadi penting nanti.

Formula untuk gelombang tanpa akhir di tempat tertentu

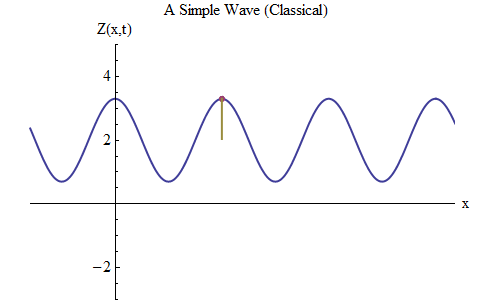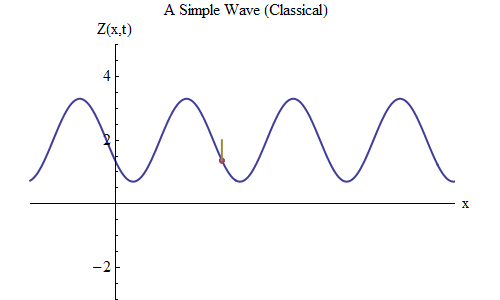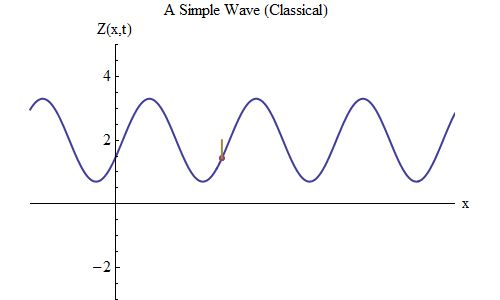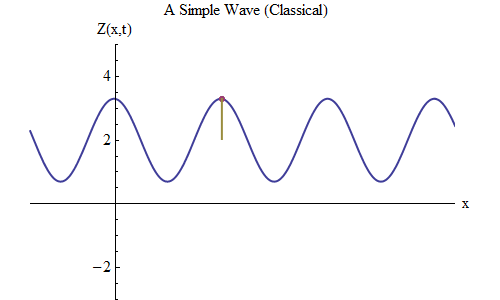Fig. 5

Sekarang mari kita ajukan pertanyaan lain: mari kita lihat bagaimana gelombang berubah dalam waktu, melacak titik tertentu pada tali, dan melihat bagaimana ia berperilaku dan bergerak. Ini ditunjukkan dalam gambar. 5: di sana saya menunjuk titik tertentu x ₀ , yang pada waktu t ₀ berada di puncak. Gelombang bergerak ke kanan dan mengikuti ukuran gelombang Z pada titik x ₀ , berubah waktu: Z (x ₀ , t). Dan Anda akan segera melihat bahwa ketinggian gelombang pada titik tertentu berperilaku persis seperti bola di pegas! Oleh karena itu, ia akan memiliki rumus yang sama persis seperti bola pada pegas, sebagai fungsi frekuensi ν, atau periode T = 1 / ν, di mana T adalah waktu antara saat ketika gelombang pada x ₀ berada di puncak dan saat ketika dia mendekati lambang lagi lain kali.

$$

$$Z (x_0, t) = Z_0 + A cos (2 \ pi \ nu t) = Z_0 + A cos (2 \ pi t / T)$$

Formula Gelombang Infinite Lengkap

Sekarang kita membutuhkan rumus untuk Z (x, t) yang menggambarkan gelombang yang digambarkan pada Gambar. 3 dan 5 (atau yang serupa) di titik x kapan saja t. Jawaban yang benar adalah:

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Ini mencakup kedua rumus, untuk titik waktu tetap dan titik tetap ruang.

Perhatikan tanda minus di depan x. Saya menyebutkan bahwa dalam rumus untuk Z (x, t ₀ ) Anda dapat mengganti minus sesuka hati. Dengan tanda minus di depan x dan tanda plus di depan t, rumus tersebut menggambarkan gelombang yang bergerak ke kanan, seperti pada animasi. Untuk memverifikasi ini, perhatikan bahwa ketika t / T - x / λ = 0, gelombang akan menjadi puncak karena cos [0] = 1. Ketika t = 0, pada titik x = 0 punggungan. Tetapi jika kita bergerak sedikit ke depan, katakanlah, pada T / 10, maka lambang akan berada di titik x = λ / 10, di sebelah kanan tempat di mana itu di t = 0 - oleh karena itu lambang (dan seluruh gelombang) bergerak ke kanan.

Apa yang akan berubah jika Anda menempatkan plus, bukannya minus dalam rumus untuk Z (x, t)? Maka puncak akan berada di t / T + x / λ = 0, dan dalam hal ini, di t = T / 10, puncak akan berada di x = -λ / 10, di sebelah kiri tempat di mana itu pada t = 0 - yang berarti , sekarang gelombang bergerak ke kiri (Gbr. 6).


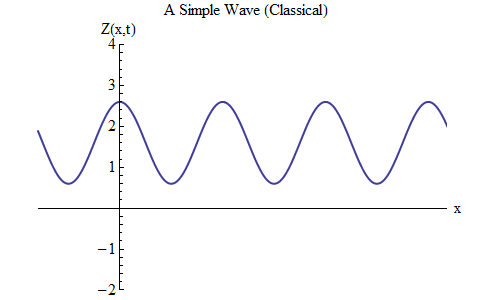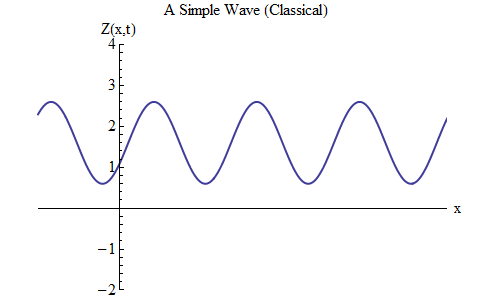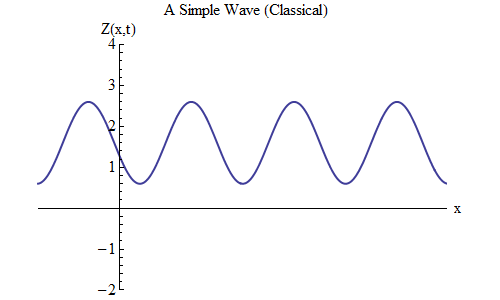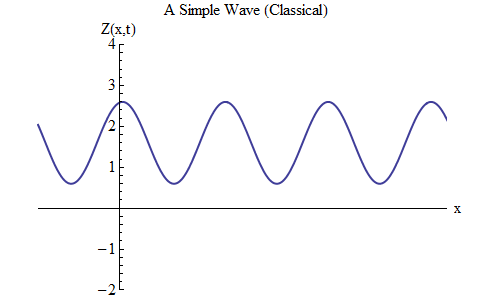Fig. 6

Gelombang, yang merupakan fungsi dari x dan t, dapat bergerak ke segala arah, jadi kita hanya perlu memilih formula yang tepat untuk gelombang yang diberikan. Secara umum, ketika kita bekerja dengan gelombang yang dapat bergerak tidak hanya sepanjang satu dimensi spasial x, tetapi sepanjang ketiga koordinat x, y dan z, maka gelombang ini dapat bergerak ke segala arah, dan kita perlu memilih formula yang tepat berdasarkan arah. gerakan gelombang.

Cetak halus: kita dapat meletakkan tanda minus di depan t, dan bukan sebelum x. Tetapi + t, + x sama dengan –t, -x, karena ini akan sama dengan mengalikan seluruh rumus di dalam cosinus dengan -1, dan cos [w] = cos [-w]. Oleh karena itu, + t, + x dan -t, -x memberikan gelombang bergerak ke kiri, dan + t, -x dan -t, + x memberikan gelombang bergerak ke kanan.

Persamaan Gelombang

Sekarang, seperti dalam kasus bola pada pegas, ketika kami pertama kali menemukan formula untuk gerak osilasi bola, dan kemudian melihat persamaan gerak, yang formula ini adalah solusinya, kami akan melakukan hal yang sama di sini. Kami menemukan formula untuk bentuk dan pergerakan gelombang. Persamaan gerak manakah di antara solusi yang memiliki formula seperti itu? Kita belajar di artikel selanjutnya.