Kami memahami fisika partikel: 4) gelombang, persamaan gerak klasik

1. Bola pada pegas, versi Newton
2. Bola kuantum pada pegas
3. Gelombang, tampilan klasik
4. Gelombang, persamaan gerak klasik
5. Gelombang kuantum
6. Fields
7. Partikel adalah kuanta
8. Bagaimana partikel berinteraksi dengan bidang

Mari kita kembali ke persamaan osilasi bola pada pegas

Dalam salah satu artikel pertama dari siklus, pertama-tama kita membuat formula untuk gerak osilasi bola

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

Dan kemudian mereka menemukan persamaan gerak yang formula ini adalah solusinya

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$$

Di sini
• d ² z / dt ² menunjukkan perubahan waktu dari perubahan waktu z (t).
• K adalah gaya pegas, M adalah massa bola, z ₀ adalah posisi kesetimbangan.
• ν = √ K / M / 2π

Langkah kunci untuk mendapatkan persamaan frekuensi terakhir yang dinyatakan dalam K dan M adalah perhitungan d2z / dt ² untuk gerak osilasi bola z (t) = z ₀ + A cos [2 π ν t]. Kami menemukan itu

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

Persamaan Gelombang

Sekarang kami ingin melakukan hal yang sama untuk gelombang. Kami menemukan formula untuk bentuk dan pergerakan gelombang yang berosilasi baik dalam ruang maupun waktu.

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Di antara solusi persamaan gerak manakah rumus seperti itu? Anda bisa membayangkan jawabannya. Jelas, itu termasuk:

1. d ² Z / dt ² , perubahan waktu, perubahan waktu Z (x, t).
2. d ² Z / dx ² , perubahan ruang perubahan dalam ruang Z (x, t).

Secara alami, kita dapat menebak bahwa persamaannya akan terlihat seperti ini:

$$

$$C_t d ^ 2Z / dt ^ 2 + C_x d ^ 2Z / dx ^ 2 = C_0 (Z - Z_0)$$

Di mana _Ct , C _x dan C ₀ adalah konstanta. Saya perhatikan bahwa jika Dimana _Ct = 1, C _x = 0, dan C ₀ = -K / M, kita akan kembali ke persamaan osilasi bola pada pegas. Apa saja konstanta ini dalam kasus kami?

Kami selalu dapat menempatkan _Ct = 1. Jika Anda ingin, katakanlah, menempatkan _Ct = 5, saya hanya akan meminta Anda untuk membagi seluruh persamaan dengan 5, yang akan memberi Anda persamaan opsi di mana _Ct = 1, hanya dengan nilai-nilai lain dari konstanta lain.

Setelah itu, ternyata nilai-nilai C _x dan C ₀ ternyata berbeda dalam sistem fisik yang berbeda. Kita akan mempelajari dua kelas gelombang yang berbeda dengan konstanta yang berbeda.

Untuk kedua kelas, C _x akan negatif, $$$C_x = -c_w ^ 2$(di sini _cw menunjukkan kecepatan pergerakan gelombang frekuensi tinggi).

Kelas-kelas ini akan berbeda karena kelas pertama, Kelas 1, C ₀ akan negatif, dan akan menjadi - (2 π μ) 2, dan yang kedua, Kelas 0, C ₀ akan menjadi nol.

Kami sekarang mempelajari sifat-sifat gelombang dari dua kelas persamaan ini. Tapi sebelum itu, kita perlu melakukan perhitungan lain, yang sudah kita lakukan sebelumnya.

Hitungan cepat

Untuk gelombang tanpa akhir kami

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Kita perlu mengetahui d ² Z / dt ² dan d ² Z / dx ² . Pada artikel sebelumnya, kami telah menunjukkan bahwa untuk bola pada pegas bergerak sesuai dengan z (t) = z ₀ + A cos [2 π ν t], ternyata $$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (z - z_0)$. Perubahan waktu memberi kita faktor 2 π ν, dan perubahan waktu memberi kita faktor dua faktor. Selain itu, ada tanda minus yang umum. Karena itu, Anda tidak akan terkejut bahwa:

• $$$d ^ 2Z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (Z - Z_0)$
• $$$d ^ 2Z / dx ^ 2 = - (2 \ pi / \ lambda) ^ 2 (Z - Z_0)$

Setiap perubahan waktu memberi kita faktor ν = 1 / T (semakin besar periode, semakin lambat perubahan waktu), dan setiap perubahan ruang memberi kita faktor 1 / λ (semakin lama gelombang, semakin lambat perubahan ruang).

Bukti

Untuk gelombang tanpa batas, kita memiliki persamaan dasar

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Dan kami ingin menunjukkan itu

$$

$$d ^ 2Z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (Z - Z_0)$$

$$

$$d ^ 2Z / dx ^ 2 = - (2 \ pi / \ lambda) ^ 2 (Z - Z_0)$$

Beberapa fakta:

• Z - Z ₀ = A cos (2π [ν t - x / λ]) (hanya dalam persamaan utama mereka memindahkan Z ₀ ke sisi kiri)
• Karena Z ₀ adalah independen konstan dari waktu dan ruang, dZ ₀ / dt = 0 dan dZ ₀ / dx = 0.
• d (cos t) / dt = - sin t, dan d (sin t) / dt = + cos t
• d (F [at + bx]) / dt = iklan (F [at + bx]) / d (a t + bx), di mana a dan b adalah konstanta, dan F adalah fungsi dari (at + bx).
• d [A f (t)] / dt = A d [f (t)] / dt, di mana f (t) adalah fungsi dari t, dan A adalah konstanta

Bersama-sama, ini berarti:

$$

$$dZ / dt = d [A cos (2 \ pi [\ nu t - x / \ lambda])] / dt = cos (2 \ pi [\ nu t - x / \ lambda])] / dt \\ = A (2 \ pi \ nu) d [cos (2 \ pi [\ nu t - x / \ lambda])] / d (2 \ pi [\ nu t - x / \ lambda]) = - ( 2 \ pi \ nu) Dosa (2 \ pi [\ nu t - x / \ lambda])$$

dan

$$

$$d ^ 2Z / dt ^ 2 = d [- (2 \ pi \ nu) Dosa (2 \ pi [\ nu t - x / \ lambda])] / dt = \\ - (2 \ pi \ nu) A d [sin (2 \ pi [\ nu t - x / \ lambda])] / dt = \\ - (2 \ pi \ nu) ^ 2 A cos (2 \ pi [\ nu t - x / \ lambda ]) = - (2 \ pi \ nu) ^ 2 (Z - Z_0)$$

Karena rumus dasar untuk gelombang tidak berubah ketika (ν t) diganti oleh (-x / λ), perhitungan d ² Z / dx ² tidak berbeda dari perhitungan d ² Z / dt ² , hanya alih-alih d / dt memberikan faktor (2π ν ), kita akan memiliki d / dx yang memberikan faktor (- 2π / λ). Tetapi, karena ada dua faktor seperti itu dalam jawaban, kami hanya mengganti (2π ν) ² dengan (- 2π / λ) ² = (+ 2π / λ) ² ; minus tidak masalah (secara keseluruhan penambahan minus tetap). Karena kami perlu membuktikan

$$

$$d ^ 2Z / dt ^ 2 = - (2 \ pi / \ lambda) ^ 2 (Z - Z_0)$$

Cetak halus: semua turunan di atas sebenarnya adalah turunan parsial.

Kelas 0: gelombang frekuensi apa pun dan kecepatan yang sama

Dalam kelas gelombang ini, persamaan geraknya adalah:

$$

$$d ^ 2Z / dt ^ 2 - c_w ^ 2 d ^ 2Z / dx ^ 2 = 0$$

Setelah menghubungkan rumus Z (x, t) untuk gelombang tak terbatas dan menggunakan perhitungan yang baru saja dibuat, kami menemukan bahwa:

$$

$$- (2 \ pi \ nu) ^ 2 (Z - Z_0) - (-c_w ^ 2) (2 \ pi / \ lambda) ^ 2 (Z - Z_0) = 0$$

Bagi persamaan dengan $$$- (2 \ pi) ^ 2 (Z - Z_0)$kita dapatkan

$$

$$\ nu ^ 2 - c_w ^ 2 / \ lambda ^ 2 = 0$$

Karena frekuensi, kecepatan, dan panjang gelombangnya positif, kita dapat mengekstrak root dan memperolehnya

ν = c _w / λ, atau, jika Anda inginkan, λ = c _w / ν = cw T

Dari rumus ini kita belajar bahwa:

• Awalnya, gelombang kami, seperti yang kami rekam, dapat memiliki frekuensi dan panjang gelombang apa pun. Namun persamaan gerak membuat mereka saling bergantung. Untuk gelombang kelas 0, Anda dapat memilih frekuensi apa pun, tetapi setelah itu panjang gelombang ditentukan melalui λ = c _w / ν.
• Semua gelombang kelas 0, terlepas dari frekuensi, bepergian dengan kecepatan _cw . Ini mengikuti dari rumus λ = _cw T dan Gambar. 3 dari artikel sebelumnya . Amati bagaimana gelombang melewati satu siklus osilasi selama satu periode T. Apa yang terjadi? Gelombang terlihat persis sama setelah T, tetapi setiap lambang telah bergeser ke tempat tetangganya berada - pada jarak λ. Ini berarti bahwa punggungan bergerak jarak λ dalam waktu T - satu panjang gelombang dalam satu periode osilasi - dan berarti punggungan bergerak dengan kecepatan λ / T = _cw . Ini berlaku untuk semua frekuensi dan periode, dan semua panjang gelombang!
• Seperti dalam kasus bola pada pegas, amplitudo A dari gelombang ini bisa berupa apa saja, semau besar atau kecil. Dan ini adalah kasus untuk semua frekuensi.

Kelas 1: gelombang dengan frekuensi lebih besar dari minimum, dengan kecepatan berbeda

Untuk kelas gelombang ini, persamaan gerak kami adalah:

$$

$$d ^ 2Z / dt ^ 2 - cw ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Mengganti rumus Z (x, t) untuk gelombang tak terbatas dan menggunakan perhitungan cepat yang ditunjukkan di atas, kami menemukan itu

$$

$$- (2 \ pi \ nu) ^ 2 (Z - Z_0) - (-cw ^ 2) (2 \ pi / \ lambda) ^ 2 (Z - Z_0) = - (2 \ pi \ mu) ^ 2 ( Z - Z_0)$$

Membagi persamaan dengan $$$- (2 \ pi) ^ 2 (Z - Z_0)$kita dapatkan

$$

$$\ nu ^ 2 - cw ^ 2 / \ lambda ^ 2 = \ mu ^ 2$$

Karena frekuensi, kecepatan, dan panjang gelombangnya positif, kita dapat mengekstrak akar kuadrat dan mendapatkan

$$

$$\ nu = [(cw / \ lambda) ^ 2 + \ mu ^ 2] ^ {1/2}$$

Biarkan saya mengingatkan Anda bahwa Anda ^1/2 sama dengan √y.

Rumus ini sangat berbeda dari rumus untuk gelombang kelas 0, seperti juga konsekuensi penerapannya.

Pertama, persamaan gerak menunjukkan adanya frekuensi minimum yang diizinkan. Karena (cw / λ) ² selalu positif,

$$

$$\ nu = [(cw / \ lambda) ^ 2 + \ mu ^ 2] ^ {1/2} ≥ \ mu$$

Untuk lebih dekat ke ν = μ, perlu untuk meningkatkan λ. Untuk panjang gelombang yang sangat besar, frekuensinya mendekati μ, tetapi tidak bisa menjadi lebih kecil. Untuk gelombang 0 kelas, ini tidak begitu. Mereka memiliki ν = cw / λ, jadi bagi mereka, semakin banyak yang Anda lakukan λ, semakin kuat ν mendekati nol. Untuk gelombang kelas 1, nilai ν lebih besar dari μ adalah mungkin.

Kedua, kami menemukan bukti bahwa semua gelombang kelas 0 memiliki kecepatan yang sama, tetapi itu tidak bekerja untuk gelombang kelas 1. Satu-satunya pilihan di mana ia dapat bekerja jika kita mengambil ν jauh lebih besar dari μ; untuk ini kita perlu membuat λ sangat kecil (dan, karenanya, 1 / λ sangat besar). Dalam hal ini

$$

$$\ nu = [(cw / \ lambda) ^ 2 + \ mu ^ 2] ^ {1/2} ≈ cw / \ lambda$$

Artinya, pada frekuensi yang sangat besar dan panjang gelombang kecil, gelombang kelas 1 akan memiliki rasio yang kira-kira sama antara frekuensi dan panjang gelombang dengan gelombang kelas 0, oleh karena itu, untuk alasan yang sama seperti gelombang kelas 0, gelombang tersebut akan bergerak dengan kecepatan , (kurang-lebih) sama dengan cw.

Apa yang benar untuk gelombang kedua kelas adalah bahwa amplitudo A dapat berupa apa saja, semau kecil atau besar, dan tidak tergantung pada frekuensi.


Fig. 1. Untuk gelombang kelas 0 dan 1, persamaan gerak memberikan hubungan antara frekuensi, atau periode, dan panjang gelombang, atau 1 / panjang gelombang. Setiap grafik menunjukkan hubungan dari nilai-nilai ini tergantung pada persamaan gerak. Tiga grafik menunjukkan hal yang sama, tetapi mereka dibangun di atas variabel yang berbeda. Garis biru mengacu pada gelombang kelas 0. Merah menunjukkan gelombang kelas 1, yang kecepatannya sama pada frekuensi sangat tinggi dan panjang gelombang pendek, ketika mereka bertepatan dengan garis biru. Tetapi pada frekuensi minimum μ (dan dengan periode maksimum 1 / μ), ditandai dengan warna hijau, kedua kurva berbeda dengan peningkatan panjang gelombang.

Cetak halus: Anda mungkin memperhatikan bahwa saya sedikit curang. Saya tidak menghitung kecepatan gelombang kelas 1. Faktanya adalah tangkapan yang sangat rumit bersembunyi di sini. Untuk gelombang kelas 0, saya menghitung kecepatan mereka, mengikuti pergerakan punggungan. Ini berfungsi karena di kelas 0, gelombang semua frekuensi bergerak pada kecepatan yang sama. Tetapi di kelas 1, atau yang lainnya, di mana gelombang dengan frekuensi berbeda bergerak dengan kecepatan berbeda, kecepatan gelombang nyata tidak ditentukan oleh kecepatan gerakan puncaknya! Ternyata bubungan bergerak lebih cepat dari cw, tetapi kecepatan gelombang kurang dari cw. Untuk memahami hal ini, perlu menggunakan logika yang sangat tidak jelas dan perbedaan antara kecepatan "grup" dan "fase". Saya akan memotong trik ini; Saya hanya ingin menarik perhatian Anda pada keberadaannya sehingga Anda tidak mendapatkan ide yang salah.

Komentar terakhir tentang gelombang klasik

Anda dapat menemukan banyak contoh gelombang Kelas 0 yang akrab, termasuk suara di udara, air atau logam (di mana cw adalah kecepatan gelombang suara dalam suatu material), cahaya, dan gelombang elektromagnetik lainnya (di mana cw = c dalam ruang hampa), dan gelombang pada tali atau string, seperti pada gambar. 2 di artikel sebelumnya. Oleh karena itu, gelombang kelas 0 diajarkan dalam kursus fisika dasar. Saya tidak bisa memberikan contoh gelombang Kelas 1 dalam kehidupan sehari-hari, tetapi kita akan segera melihat bahwa gelombang ini juga penting bagi Semesta.

Kami memiliki rumus yang mudah digunakan E = 2 π ² ν ² A ² M untuk energi bola massa M pada pegas. Rumus untuk osilator lain bergantung pada sifatnya, tetapi bentuknya hampir sama. Tetapi dalam kasus ombak, kami tidak menyebutkan energi mereka. Khususnya, karena kami mempelajari gelombang dengan jumlah bubungan yang tidak terbatas untuk menyederhanakan matematika. Secara intuitif, beberapa jenis energi harus disimpan dalam gerakan dan bentuk setiap lambang dan palung, dan dengan jumlah puncak dan palung yang tak terbatas, jumlah energi dalam gelombang akan menjadi tak terbatas. Ada dua cara untuk mengatasi hal ini. Rumus yang tepat tergantung pada jenis gelombang, tetapi mari kita lihat gelombang kelas 0 pada tali.

• Jumlah energi per panjang gelombang (disimpan antara titik x dan titik x + λ), tentu saja, sama dengan 2 π ² ν ² A ² M _λ , di mana M _λ adalah massa segmen tali dengan panjang λ.
• Pada kenyataannya, gelombang tidak terbatas. Sebagai dorongan dari beberapa punggung bukit dan depresi, ditunjukkan pada Gambar. 2 dalam artikel terakhir, gelombang apa pun akan terbatas, ia akan memiliki jumlah punggungan dan depresi yang terbatas. Jika membentang ke panjang L, yaitu, ia akan memiliki punggungan L / λ, maka energi yang ditransfer ke sana akan menjadi 2 π ² ν ² A ² M _L , di mana M _L adalah massa seutas tali dengan panjang L. Ini hanya L / λ, dikalikan dengan energi dengan satu panjang gelombang.

Untuk gelombang yang merambat keluar dari tali, detail persamaan akan berbeda, tetapi energi per panjang gelombang sistem osilasi sederhana akan selalu proporsional dengan ν ² A ² .

Di kelas 1, ada gelombang yang sangat menarik, yang tidak ada di kelas 0. Ini adalah kasus ketika ν = μ, nilai minimum, dan λ = tak terhingga. Dalam hal ini, gelombang berbentuk

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi \ mu t)$$

Gelombang ini tidak bergantung pada x kapan saja, yaitu, Z (x, t) akan menjadi konstan di seluruh ruang, dan Z berosilasi dalam waktu seperti bola pada pegas dengan frekuensi μ. Gelombang stasioner seperti itu, ditunjukkan pada Gambar. 2, akan sangat penting dalam pertimbangan lebih lanjut.


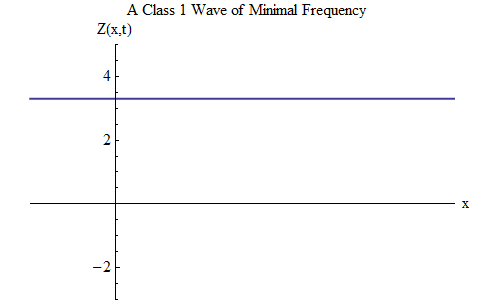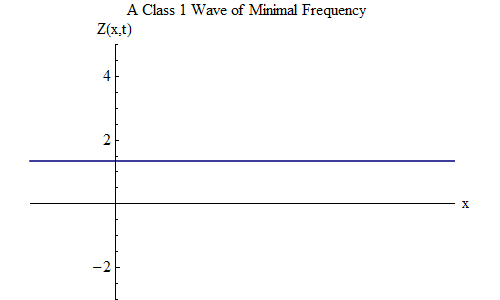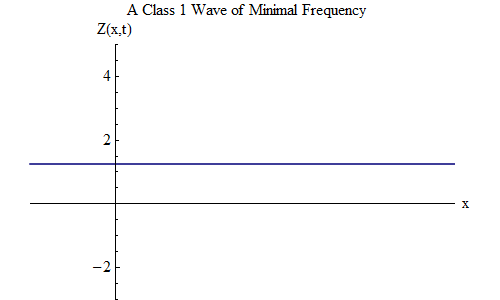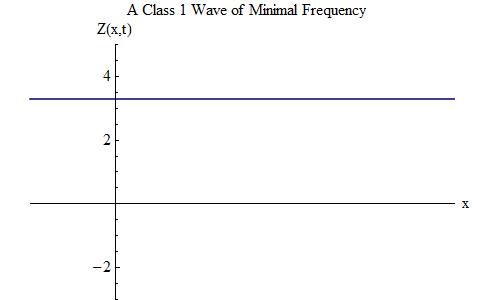Fig. 2

Gelombang kuantum

Untuk bola pada pegas, perbedaan antara sistem klasik dan sistem kuantum adalah bahwa dalam kasus pertama, amplitudo dapat mengambil nilai acak, seperti energi, dan dalam kasus kuantum, amplitudo dan energi dikuantisasi. Untuk sistem osilasi yang serupa, ini bekerja dengan cara yang sama. Mungkin kita dapat menebak bahwa ini juga berlaku untuk ombak ...