Kami memahami fisika partikel: 6) bidang

1. Bola pada pegas, versi Newton
2. Bola kuantum pada pegas
3. Gelombang, tampilan klasik
4. Gelombang, persamaan gerak klasik
5. Gelombang kuantum
6. Fields
7. Partikel adalah kuanta
8. Bagaimana partikel berinteraksi dengan bidang

Bahkan, kami pergi ke wilayah ladang beberapa waktu lalu, saya hanya tidak memperingatkan Anda tentang hal itu - saya ingin berkonsentrasi pada gelombang yang muncul di bidang ini. Menjelaskan bagaimana gelombang berperilaku, kami menyatakan bentuk dan ketergantungannya pada waktu menggunakan fungsi Z (x, t). Nah, Z (x, t) adalah bidang. Ini adalah fungsi ruang dan waktu dengan persamaan gerak yang menentukan perilakunya. Fungsi gerak yang sesuai adalah sedemikian rupa sehingga jika Z meningkat atau menurun pada titik tertentu, maka Z akan menurun atau meningkat pada titik-titik tetangga beberapa saat kemudian. Fitur ini memungkinkan gelombang untuk menjadi solusi persamaan.

Pada artikel ini, kita akan melihat beberapa contoh bidang Z (x, t) yang persamaan geraknya memungkinkan kehadiran gelombang. Interpretasi fisik dari bidang-bidang ini akan sangat berbeda. Mereka menggambarkan sifat yang berbeda dari bahan yang berbeda. Tetapi persamaan yang mereka puaskan, dan gelombang yang mereka tunjukkan, akan memuaskan matematika yang sangat mirip, dan mereka akan berperilaku sama, terlepas dari asal-usul fisik mereka yang berbeda. Ini akan menjadi poin yang sangat penting di masa depan.

Dan kemudian kita melakukan sesuatu yang radikal - pertimbangkan bidang dalam konteks teori relativitas khusus. Seperti yang diperlihatkan Einstein, jika Anda mengoreksi ruang dan waktu dan memaksa mereka untuk memimpin bukan dengan cara yang diharapkan kebanyakan orang, Anda akan mendapatkan jenis bidang baru - sedemikian rupa sehingga interpretasi fisiknya bukan properti dari apa pun, melainkan objek fisik independen.

Bidang biasa menggambarkan hal-hal biasa

Bidang Z (x, t) dapat mewakili banyak kuantitas fisik yang berbeda. Sebagai contoh:
• Tinggi tali membentang melintasi ruangan.
• Ketinggian air di sungai.
• Kepadatan kristal atau gas.
• Posisi atom dalam magnet.
• Kecepatan angin.
• Suhu, kepadatan atau tekanan udara.

Dalam salah satu kasus ini, ada bidang Z (x, t): bidang ketinggian, bidang kerapatan, bidang orientasi, bidang angin, dan bidang suhu. Nilainya dalam bentuk fungsi ruang dan waktu memberi tahu kita ketinggian, kepadatan, orientasi, kecepatan angin atau suhu medium tertentu - tali, sungai, kristal, gas, magnet, udara - di semua tempat pada waktu tertentu. Persamaan geraknya menunjukkan bagaimana Z (x, t) dapat berperilaku pada prinsipnya. Ini juga menunjukkan bagaimana memprediksi perilaku Z (x, t) di masa depan, jika kita tahu persis perilakunya di masa kini dan masa lalu.

Dalam setiap contoh, ada bidang dan lingkungan, dan kita tidak boleh membingungkan bidang dengan lingkungan. Bidang hanya menggambarkan dan mencirikan salah satu dari banyak properti dari lingkungan yang sesuai. Lingkungan yang benar-benar berbeda dapat memiliki bidang perilaku yang sangat mirip dengan gelombang yang sangat mirip - kita masih akan melihatnya.

Sekali lagi saya akan mengklarifikasi hal yang sering menyebabkan kesalahpahaman. Secara umum, bidang mungkin tidak ada hubungannya dengan jarak fisik di ruang. Ya, dalam artikel 3 dan 4, saya menggunakan contoh seekor sapi di atas tali untuk menggambarkan apa itu Z (x, t), karena itu indah dan intuitif. Saya juga sering memplot grafik Z (x, t) untuk gelombang. Ini dapat memberi Anda kesan salah bahwa Z (x, t) selalu dikaitkan dengan gelombang yang menyebabkan objek fisik (seperti tali) untuk memindahkan jarak Z ke arah yang tegak lurus terhadap sumbu x. Tetapi tidak demikian, karena tiga dari empat contoh kita akan menunjukkan kepada kita.

Bidang Tinggi Tali

Pertama, perhatikan contoh awal kita tentang gelombang, tali berosilasi. Dalam hal ini, peran Z (x, t) adalah bidang tinggi, yang kita sebut H (x, t). Ini memberitahu kita ketinggian tali di setiap titik di ruang pada sumbu x yang berjalan di sepanjang tali kapan saja t. Jika tali berada pada ketinggian ekuilibrium H ₀ , maka H (x, t) = H ₀ . Bidang ketinggian adalah konstan dalam ruang dan waktu. Jika gelombang sederhana bergerak melewatinya, maka bidang ketinggian akan dijelaskan oleh rumus gelombang terkenal kami dari artikel sebelumnya.

Jika kita tahu H (x, t), kita tahu ketinggian tali di semua titik dalam ruang dan waktu. Jika kita tahu apa yang sedang dilakukan tali sekarang dan apa yang telah dilakukan baru-baru ini, dengan menggunakan persamaan gerak kita dapat memprediksi apa yang akan dilakukan tali di masa depan. Ini memberi tahu kita sedikit tentang tali itu sendiri. Bidang ketinggian memberi kita hanya apa yang namanya tersirat: ketinggian tali. Tali adalah media fisik yang tingginya direpresentasikan sebagai bidang H (x, t); itu tidak memberi tahu kita apa-apa tentang warna tali, ketebalan, tegangan, bahan, dll.

Dalam gbr. 1 Aku buatkan untukmu animasi gelombang di bidang tinggi dari kiri ke kanan. Tampaknya saya melukis hal yang sama dua kali, pertama berwarna hijau dan kemudian oranye. Tapi ini bukan hal yang sama. Kurva oranye adalah tali itu sendiri, bergerak di ruang fisik. Kurva hijau adalah grafik yang mewakili apa yang terjadi dengan H (x, t), terlepas dari apa yang H (x, t) (yaitu, tinggi) artinya, atau lingkungan seperti apa itu. Dan hanya dalam kasus ini, grafik hijau terlihat persis sama dengan apa yang terjadi di dunia fisik. Tetapi dalam semua kasus lain, ini tidak akan terjadi.


Fig. 1

Bidang Pemindahan Kisi

Misalkan kita memiliki media yang terdiri dari kristal dengan atom yang terdistribusi secara seragam pada jarak yang sama satu sama lain. Saya menggambar mereka di foto. 2 dalam satu dimensi - Anda dapat membayangkan situasi serupa dengan tiga dimensi, tetapi untuk saat ini ini akan menjadi komplikasi yang tidak perlu. Saya juga menandai setiap atom ke-10 berwarna merah untuk memudahkan Anda melacak pergerakannya. Dan saya juga sangat melebih-lebihkan jarak antara atom - bayangkan bahwa antara setiap dua titik merah ada beberapa juta atom, bukan 10.

Kita melihat medan perpindahan D (x, t), yang memberi tahu kita berapa banyak pada saat t atom, biasanya terletak pada titik kesetimbangan x, telah bergerak dari titik ini dalam kisi. Ini berarti bahwa dalam kasus keadaan statis dari mana animasi dimulai, bidang di mana-mana nol, D (x, t) = 0, karena semua atom berada di posisi biasanya. Kemudian, dalam animasi, masing-masing atom mulai berosilasi bolak-balik, dan gerakan mereka, pada umumnya, merambat dalam bentuk gelombang yang bergerak dari kiri ke kanan. Di bagian atas gambar, grafik bidang perpindahan kisi D (x, t) menunjukkan bagaimana medan berperilaku selama lewatnya gelombang. Perhatikan bahwa bidang pada Gambar. 1 dan 2 berperilaku serupa, meskipun interpretasi fisik bidang sangat berbeda.


Fig. 2

Bidang orientasi magnetik

Apa itu magnet permanen? Ini terdiri dari satu set atom, yang masing-masing berfungsi sebagai magnet kecil dengan medan magnet kecil, dan mereka semua disejajarkan sehingga bersama-sama mereka menciptakan medan magnet besar. Magnet ditunjukkan pada gambar. 3, dan di dalamnya setiap atom diarahkan ke atas. Dalam kasus ini, bidang orientasi Θ (x, t) memberi tahu kita seberapa jauh waktu t atom pada titik x menyimpang dari vertikal. Θ, singkatnya, akan menjadi sudut antara magnet masing-masing atom dan vertikal. Animasi dalam gbr. Gambar 3 menunjukkan gelombang dalam magnet di mana arah magnet atom berosilasi ke kiri dan kanan. Grafik Θ (x, t) ditampilkan di atas magnet hijau; dan lagi-lagi dia terlihat persis sama dengan kasus-kasus sebelumnya.

Medan tekanan udara

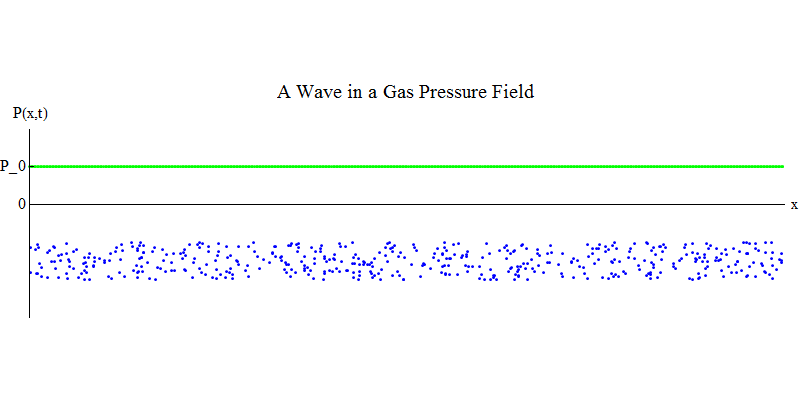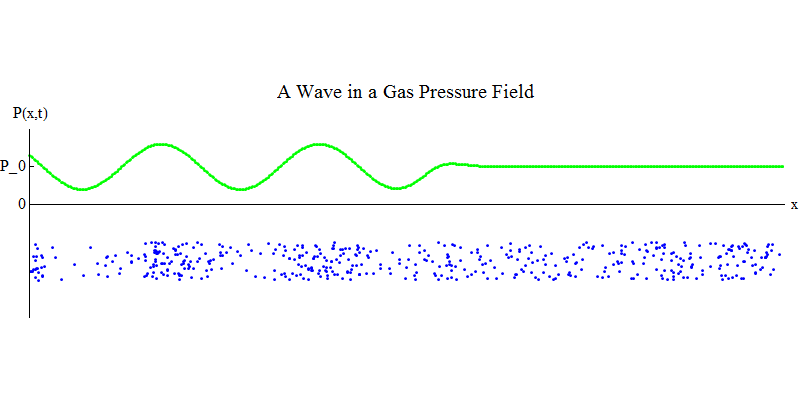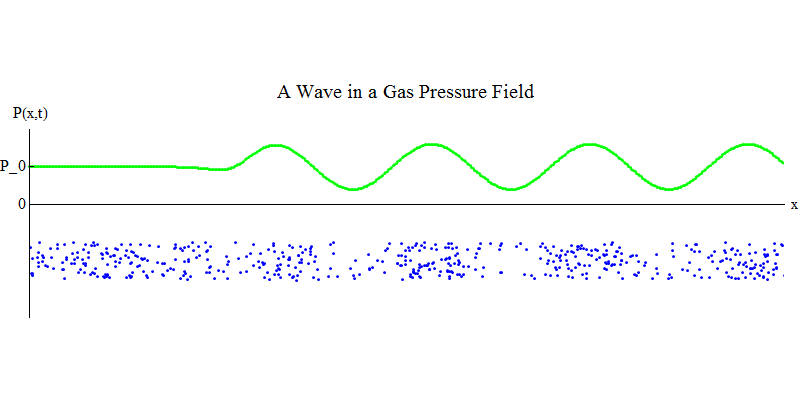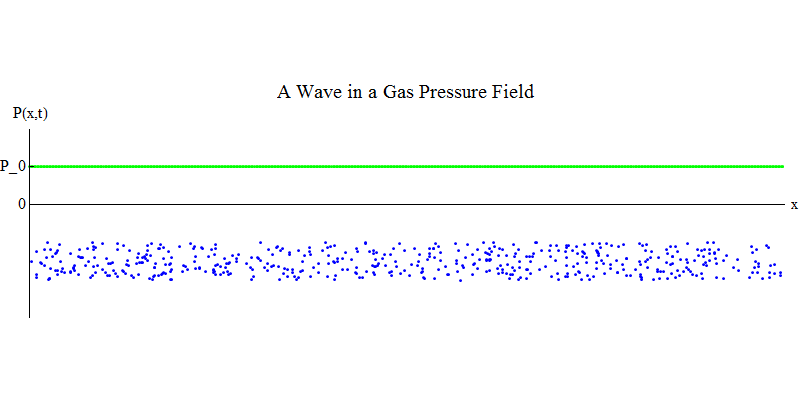
Pertimbangkan gas molekul dalam pipa panjang. Di sepanjang pipa akan menjadi dimensi x. Molekul gas akan bergerak hampir secara acak, bertabrakan dengan dinding pipa dan dengan satu sama lain. Dalam kesetimbangan, densitas (jumlah molekul dalam volume tertentu) dan tekanan P (x, t) (gaya yang bekerja pada permukaan bola kecil yang muncul pada titik x pada waktu t) adalah konstan. Tetapi gelombang suara yang melewati gas akan menyebabkan tekanan dan kepadatan berosilasi, seperti yang ditunjukkan pada gambar. 4. Kepadatan dan tekanan meningkat dan menurun secara berkala. Molekul bergerak maju dan mundur, meskipun rata-rata mereka tidak bergerak sama sekali, tetapi pada saat yang sama gelombang dan energinya bergerak dari kiri ke kanan melalui gas. Grafik P (x, t) terlihat sangat mirip dengan yang sebelumnya.

Pelajaran penting

Apa yang dapat kita pelajari dari empat contoh yang menunjukkan gelombang kelas 0? (Persamaan gerak memiliki satu kuantitas, cw, dan semua gelombang dalam bidang yang sesuai bergerak dengan kecepatan cw. Bidang yang berbeda dari kelas 0 akan memiliki nilai cw yang berbeda). Kita dapat mengetahui bahwa perilaku bidang yang sama dapat muncul dari bidang yang berbeda secara fisik yang ada di lingkungan yang berbeda secara fisik. Terlepas dari asal-usulnya yang berbeda, gelombang di bidang ketinggian, di bidang pemindahan kisi, di bidang orientasi magnetik, dan di bidang tekanan gas terlihat identik dari sudut pandang medan. Mereka memenuhi jenis persamaan gerak yang sama dan hubungan numerik frekuensi dan panjang gelombang yang sama.

Cetak kecil: secara tegas, jika Anda membuat gelombang dengan panjang yang cukup pendek, Anda masih dapat membedakan perilaku media yang berbeda. Begitu panjang gelombangnya sama dengan jarak antara atom-atom tali, atau kristal, atau magnet, persamaan gelombang yang akan dipenuhi gelombang akan lebih kompleks daripada yang ditulis oleh kami, dan detailnya akan membedakan media satu sama lain. Tetapi seringkali dalam percobaan praktis kita bahkan tidak mendekati untuk mengamati efek seperti itu.

Hasil dari ini adalah bahwa studi gelombang dan kuanta mereka terkait dengan bidang tidak akan selalu memberi tahu Anda apa yang berfungsi sebagai media, atau apa interpretasi fisik dari bidang tersebut - yang mana dari sifat-sifat media yang diwakilinya. Dan bahkan jika Anda entah bagaimana tahu bahwa ini adalah bidang tipe tertentu - misalnya, bidang tekanan - Anda biasanya masih tidak dapat mengetahui dari perilakunya tekanan apa yang diwakilinya. Yang bisa Anda pelajari dengan mempelajari ombak adalah apakah bidang tersebut milik kelas 0 atau kelas 1, dan berapa nilai cw; atau cari tahu bahwa bidang tersebut milik kelas lain.

Dalam beberapa kasus, ini sangat buruk; bidang ini hanya mengirimkan informasi parsial tentang lingkungan. Ini terkadang cukup nyaman; lapangan adalah hal yang lebih abstrak dan universal daripada materi fisik yang digambarkannya.

Oleh karena itu, bidang tidak mendefinisikan lingkungan, dan perilakunya sering tidak bergantung pada detail dan properti lingkungan. Karena pertanyaan apa yang muncul.

Mungkinkah ada medan fisik - dengan gelombang yang terdiri dari kuanta bergerak di ruang dan mentransfer energi - tanpa media yang mendukungnya?

Bidang tanpa media?

Anda tidak dapat mendengar lagu tanpa penyanyi. Tetapi lagu itu memiliki semacam keberadaan independen; kedengarannya berbeda, tergantung pada siapa yang menyanyikannya, tetapi pada saat yang sama ada sesuatu yang melekat dalam lagu, beberapa kualitas abstrak, berkat yang selalu dapat dikenali. Entitas abstrak ini adalah melodi dari lagu tersebut. Kita bisa berdiskusi, belajar, belajar melodi, merekamnya dengan rekaman musik, bahkan tanpa mendengarnya dilakukan oleh penyanyi. Banyak dari kita bahkan dapat menyenandungkannya di kepala kita. Entah bagaimana melodi ada bahkan jika tidak ada yang melakukan lagu.

Jika dalam semua contoh yang diberikan oleh saya dan dalam semua contoh yang dapat saya berikan, dan yang secara intuitif akan jelas bagi Anda, bidang tersebut menggambarkan properti di antara, lalu bagaimana mungkin sebuah bidang ada tanpa lingkungan? Tetapi bagaimanapun juga bidang-bidang itu tidak tergantung pada lingkungan mereka, karena banyak bidang yang berbeda dapat berperilaku sama, meskipun fakta bahwa mereka menggambarkan banyak sifat berbeda dari lingkungan yang sama sekali berbeda. Jadi, mungkin saja untuk mengabstraksi bidang dari lingkungan.

Bahkan, ini tidak hanya mungkin, tampaknya perlu. Paling tidak, perlu baik untuk tidak memiliki media, atau untuk memiliki lingkungan yang tidak dapat dibuat dari materi biasa, yang secara fundamental berbeda dari semua media yang kami pertimbangkan, karena berfungsi sedemikian rupa (menurut semua eksperimen) sehingga tidak ada. .

Salah satu dari beberapa elemen radikal teori relativitas khusus Einstein dari tahun 1905 adalah gagasan bahwa untuk gelombang cahaya - selama beberapa dekade dianggap sebagai gelombang di medan listrik dan magnet (gelombang elektromagnetik), dan bergerak dengan kecepatan yang sama di ruang kosong - tidak ada media. Hanya ada bidang.

Media hipotetis disebut "eter"; Einstein berpendapat bahwa hal semacam itu tidak ada, dan menuliskan seperangkat persamaan yang tidak diperlukan. Saya perhatikan bahwa masih ada perdebatan (seringkali lebih filosofis daripada fisik) tentang perlu tidaknya Anda membayangkan keberadaan beberapa lingkungan aneh yang sangat berbeda dari materi biasa. Hingga saat ini, tidak ada bukti yang mensyaratkan ketersediaannya.

Elemen kunci dari versi relativitas Einstein (berbeda dengan versi Galileo dan Newton) adalah sebagai berikut:

• Ruang dan waktu bukan seperti yang Anda pikirkan. Pengamat yang berbeda bergerak seragam relatif satu sama lain akan berbeda dalam estimasi panjang objek dan interval waktu antara peristiwa (dan perbedaan ini dapat diukur secara akurat).
• Ada batas kecepatan universal, s; pengamat yang mengukur kecepatan suatu objek sehubungan dengan itu akan menemukan bahwa kecepatan ini kurang dari atau sama dengan s.
• Dalam dunia seperti itu, bidang-bidang tertentu - “bidang relativistik” - dapat eksis tanpa medium, dan bidang-bidang tersebut memenuhi persamaan gerak khusus. Bidang relativistik yang paling sederhana memenuhi persamaan gerak kelas 0 atau 1, dengan kecepatan gelombang cw yang disebutkan dalam persamaan gerak yang mengambil nilai c.

Singkatnya, ada bidang relativistik kelas 0 yang memenuhi persamaan

$$

$$Kelas 0: \; d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

Cahaya, dan semua gelombang elektromagnetik, adalah contoh yang paling terkenal, tetapi bukan unik - karena itu, "c" sering disebut "kecepatan cahaya". Dan ada bidang relativistik kelas 1 yang memuaskan persamaan

$$

$$Kelas 1: \; d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Kita akan melihat contoh mereka di artikel selanjutnya. Perhatikan bahwa relativitas tidak memaksakan pembatasan pada μ (kecuali untuk kebutuhan μ2 menjadi positif) atau pada Z0. Untuk bidang relativistik, ada persamaan yang lebih kompleks, tetapi kebanyakan dari mereka dalam deskripsi proses fisik sederhana direduksi menjadi satu dari dua ini.

Bidang relativistik secara fisik nyata dan memiliki makna fisik di Semesta, yaitu:

• Gelombang mereka membawa energi dan informasi dari satu tempat ke tempat lain.
• Gelombang di satu bidang dapat memengaruhi bidang lain dan mengubah proses fisik yang akan terjadi jika tidak ada.

Tetapi, tidak seperti bidang, contoh yang diberikan dalam artikel ini, bidang relativistik tidak menggambarkan properti media fisik biasa, yang terdiri dari sesuatu yang menyerupai materi biasa, dan, sejauh yang diketahui secara eksperimental, mereka tidak menggambarkan sifat apa pun. tidak peduli apa. Bidang-bidang ini, mungkin, sejauh yang kita ketahui hari ini, adalah salah satu elemen mendasar dari Alam Semesta.