Kami memahami fisika partikel: 8) bagaimana partikel berinteraksi dengan bidang

Memahami fisika partikel:
1. Bola pada pegas, versi Newton
2. Bola kuantum pada pegas
3. Gelombang, tampilan klasik
4. Gelombang, persamaan gerak klasik
5. Gelombang kuantum
6. Fields
7. Partikel adalah kuanta
8. Bagaimana partikel berinteraksi dengan bidang

Bagaimana cara kerja bidang Higgs:
1. Gagasan utama

Dalam artikel sebelumnya dalam seri ini, saya menjelaskan bahwa partikel-partikel alam adalah kuanta dari bidang relativistik yang memenuhi persamaan gerak kelas 0 dan kelas 1. Namun apa yang belum saya katakan sejauh ini, sehingga pernyataan ini, untungnya, hanya sebagian yang benar. Persamaan nyata selalu sedikit lebih rumit, sehingga interkoneksi partikel dan bidang tetap ada, tetapi fenomena dan proses yang jauh lebih beragam menjadi mungkin, termasuk penampilan partikel setelah tumbukan partikel lain, peluruhan partikel menjadi partikel lain, dan hamburan partikel satu sama lain, serta pembentukan benda-benda menarik seperti proton dan neutron, inti atom dan atom. Saya tidak akan bisa menjelaskan semua ini secara terperinci, tetapi dalam artikel ini saya akan memberi Anda pengantar tentang bagaimana semua ini bekerja.

Perbedaan utama antara persamaan, yang saya sebut "kelas 0" dan "kelas 1", dan persamaan yang signifikan untuk fisika nyata, adalah bahwa dalam persamaan nyata ada istilah tambahan yang bergantung pada dua atau lebih bidang, dan bukan hanya satu . Katakanlah, alih-alih persamaan kelas 0 untuk bidang relativistik Z (x, t), yang terlihat seperti

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

untuk bidang nyata, persamaannya lebih seperti ini:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = y Z Z (x, t) ^ 3 + y A (x, t) B (x, t)$$

Di mana y dan y 'adalah angka (biasanya kurang dari 1), Z adalah notasi singkat dari Z (x, t), dan A (x, t) dan B (x, t) adalah sepasang bidang lainnya. Dalam persamaan seperti itu, orang dapat mengharapkan munculnya istilah seperti A (x, t) Z (x, t), atau A (x, t) ² Z (x, t), atau Z (x, t) ² , atau bahkan A (x, t) d ² Z / dt ² , dll. Anggota mana yang dapat dan mana yang tidak dapat muncul, tergantung pada detail bidang yang terlibat dalam proses. Aturannya ketat, tapi agak membingungkan, jadi kita tidak akan membahasnya untuk saat ini. Secara umum, dari percobaan yang kami lakukan (dan dipahami dari sudut pandang teoretis) bahwa pada dasarnya:

• Setiap istilah yang berlaku secara prinsip (kekekalan muatan listrik atau korespondensi relativitas Einstein) muncul dalam persamaan,
• tetapi anggota dengan banyak bidang biasanya sangat kecil dan tidak signifikan dibandingkan dengan anggota dengan satu, dua, dan kadang-kadang tiga bidang (anggota dengan turunan waktu atau ruang juga biasanya kecil).

Oleh karena itu, dalam sebagian besar proses fisik yang menarik, seseorang dapat fokus pada semua istilah yang valid dengan satu, dua, atau tiga bidang.

Sedikit terminologi. Istilah dalam persamaan dengan bidang disebut linier pada tingkat pertama. Semua istilah dalam persamaan 0 atau 1 kelas kami adalah linear. Anggota dengan dua atau tiga bidang disebut kuadrat atau kubik; secara umum, mereka disebut nonlinier. Semua fenomena menarik dunia kita muncul karena istilah-istilah nonlinier dalam persamaan gerak - yaitu, interaksi medan satu sama lain dan dengan diri mereka sendiri. Mari kita pelajari salah satunya.

Munculnya gelombang baru dari resonansi dua lainnya

Untuk mendapatkan gambaran betapa menariknya segala sesuatu bisa terjadi, kita mengambil tiga bidang, A (x, t), B (x, t), C (x, t), dan situasi yang disederhanakan. Misalkan bidang A dan B kira-kira memenuhi persamaan kelas 0 (dan mengandung kuanta tanpa massa), dan bidang C memenuhi persamaan kelas 1 (berisi gelombang dengan frekuensi minimum ν _min , dan, dengan demikian, kuanta dengan massa m = h ν _min / c ² , di mana h - Konstanta Planck). Kami juga akan menambahkan istilah nonlinier ke persamaannya. Secara khusus, seperti ini (untuk singkatnya, kami akan menulis "A" dan bukan "A (x, t)," dan seterusnya, c adalah kecepatan cahaya, y adalah angka yang biasanya kurang dari 1):

$$

$$d ^ 2A / dt ^ 2 - c ^ 2 d ^ 2A / dx ^ 2 = y BC \\ d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y AC \\ d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y AB$$

Cetak halus: Saya menambahkan istilah nonlinier ke ketiga persamaan karena keberadaan istilah tersebut di salah satu persamaan dan tidak adanya mereka di yang lain akan menyebabkan kontradiksi; misalnya, energi tidak akan dilestarikan. Untuk proses yang saya jelaskan, kita hanya perlu mempertimbangkan istilah nonlinear dalam persamaan gerak bidang C.

Mari kita lihat apa yang terjadi dengan seperangkat persamaan jika gelombang bidang A memenuhi gelombang bidang B. Pada prinsipnya, kita bisa menebak ini dengan menerapkan metode pemeriksaan dekat. Jika ada gelombang di bidang A, maka A (x, t) bukan nol di dekatnya. Ketika gelombang bidang A dan B saling tumpang tindih, hasil dari mengalikan A (x, t) dan B (x, t) menjadi nol. Sekarang kita beralih ke persamaan untuk C: perubahan dalam bidang C dalam waktu dan ruang (dua istilah di sisi kiri) dikaitkan dengan produk A dan B (salah satu istilah di sisi kanan).

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Jadi, bahkan jika bidang C adalah nol ketika A (x, t) B (x, t) menjadi tidak nol, maka C (x, t) akan segera menjadi bukan nol di bagian yang sama. Singkatnya, sebagai hasil pertemuan gelombang A dan B, gangguan kecil tertentu dari bidang C akan terjadi.

Cetakan kecil: Anda mungkin tertarik pada - setelah C menjadi bukan nol, apakah istilah A (x, t) C (x, t) menjadi persamaan gerak untuk bidang tersebut. Ini menyebabkan gangguan tambahan pada bidang B. Jawabannya adalah ya, tetapi efek ini akan bahkan lebih kecil. Sampai kita mengabaikannya, dan kemudian mencari tahu mengapa itu layak dilakukan.

Dalam gbr. Gambar 1 menunjukkan gelombang dengan frekuensi ν di bidang A (hijau), yang terjadi dengan gelombang frekuensi ν di bidang B (biru). Saya menyamakan frekuensi untuk kesederhanaan dan simetri. Nanti kita akan melihat mengapa kasus-kasus lain turun ke sini. Kecepatan ν dapat diperkirakan dengan mengamati gelombang hijau dan garis vertikal yang terletak pada satu titik dalam ruang dan berosilasi dengan gelombang.

Produk oranye di bawah ini menunjukkan produk A (x, t) B (x, t); dapat dilihat bahwa itu menjadi nol ketika dua gelombang ditumpangkan. Terlihat juga waktu bervariasi. Anda dapat melihat (membandingkannya dengan bilah vertikal berosilasi) bahwa A (x, t) B (x, t) berosilasi dua kali lebih cepat. Ingat fakta penting ini. Dalam kasus umum, jika gelombang frekuensi ν ₁ memenuhi gelombang frekuensi ν ₂ , maka produk mereka akan berosilasi dengan frekuensi ν ₁ + ν ₂ . Dan satu hal lagi: Anda dapat melihat bahwa getaran AB tidak bergerak ke kanan atau kiri, mereka tetap di tempatnya. Nanti kita akan melihat mengapa ini penting.


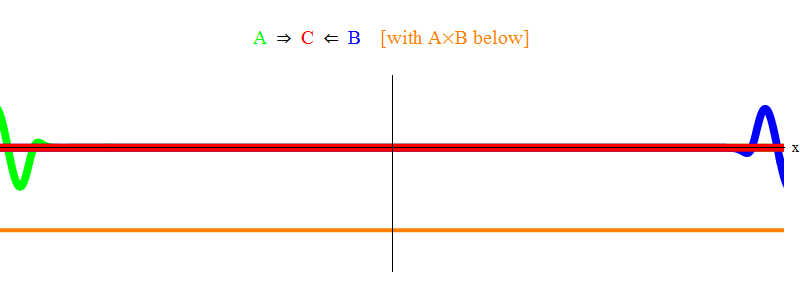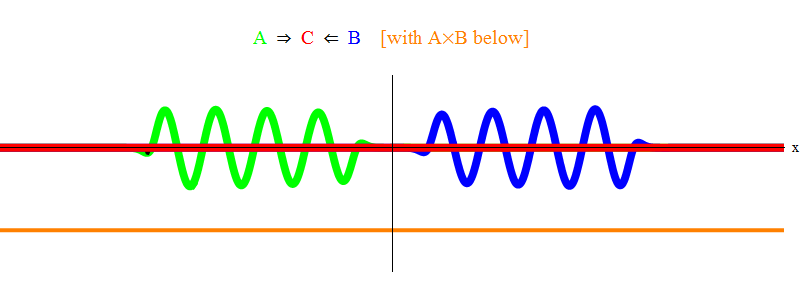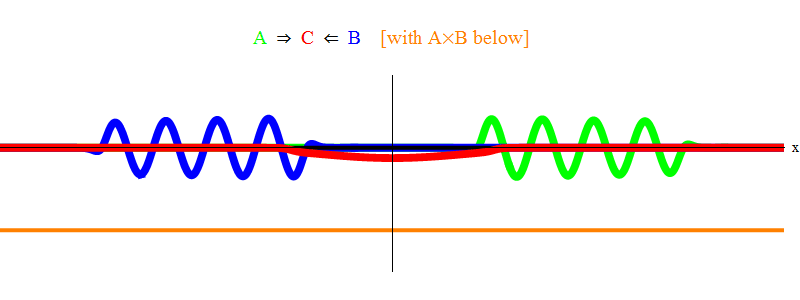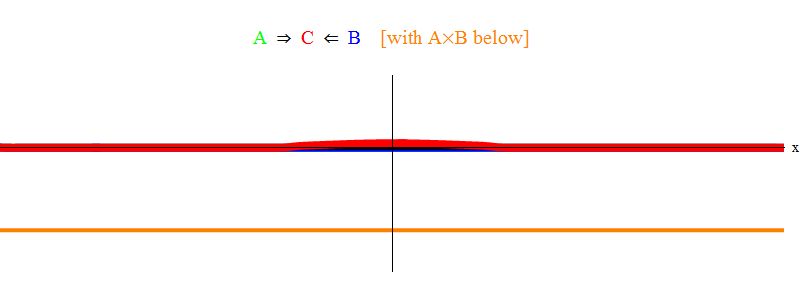Fig. 1

Bagaimana nilai AB yang tidak nol mempengaruhi C? Jawabannya sangat tergantung pada frekuensi ν. Pertama saya akan memberi Anda jawaban yang siap, dan kemudian penjelasan tentang alasannya. Ini sebenarnya adalah resonansi . Resonansi adalah fenomena integral dari semua getaran (vibrasi), termasuk gelombang. Saya telah menjelaskan bagaimana bola pada pegas berosilasi dengan frekuensi alami, dan bagaimana gaya getaran yang mendorong bola dapat menyebabkan resonansi jika frekuensi osilasi gaya bertepatan dengan frekuensi alami bola pada pegas.

Setelah memahami resonansi, Anda akan melihat bahwa bidang C, berosilasi dengan frekuensi minimum dan kecepatan nol horisontal, berperilaku seperti bola pada pegas, dan AB berperilaku seperti gaya berosilasi yang mencoba membuat bola berosilasi. Oleh karena itu, fenomena resonansi terjadi jika frekuensi getaran AB - 2ν - adalah frekuensi minimum bidang C - ν _min . Lebih khusus:

• Jika 2 ν tidak sama dengan ν _min - jika gaya tidak beresonansi - maka di daerah di mana AB tidak sama dengan nol, C akan mulai berfluktuasi secara tidak teratur, dengan amplitudo kecil.
• Jika 2 ν = ν _min - jika gaya berada dalam resonansi - maka C akan berosilasi dengan lancar, dengan amplitudo besar, di area di mana AB tidak sama dengan nol, dan akan terus berfluktuasi bahkan ketika AB menjadi nol lagi.

Fig. 1 hanya menunjukkan situasi resonansi 2 ν = ν _min . Dapat dilihat bahwa ketika gelombang A melewati gelombang B, mereka meninggalkan gelombang stasioner C, berosilasi dengan frekuensi ν _min . Cetak halus: dalam gambar sketsa ditampilkan, bukan solusi tepat dari persamaan. Solusi yang tepat akan memiliki banyak fitur kompleks kecil yang menaungi makna fisik dasar, jadi saya menghapusnya untuk kejelasan. Nanti kita akan mempertimbangkan situasi tanpa resonansi, yang jauh lebih rumit, tetapi juga lebih penting bagi fisika.

Munculnya partikel baru dari penghancuran dua lainnya

Saya baru saja menunjukkan kepada Anda bahwa istilah nonlinier AB dalam persamaan C dapat menyebabkan superposisi gelombang A dan B menghasilkan osilasi bidang C jika jumlah frekuensi bidang A dan B sama dengan frekuensi minimum bidang C. Tapi bagaimana jika gelombang ini memiliki amplitudo sangat kecil? Apa yang bisa terjadi jika satu kuantum medan A memenuhi satu kuantum medan B?

• Jika frekuensi AB memasuki resonansi dengan bidang C, maka kuantum bidang C dapat terjadi, yaitu, partikel C nyata, dan kuanta A dan B akan menghilang - "musnahkan".
• Juga, kuanta A dan B dapat saling melewati satu sama lain, tanpa membuat partikel C.
• Hukum mekanika kuantum menunjukkan bahwa probabilitas penciptaan partikel C sebanding dengan kuadrat y, yang dikalikan dengan AB dalam persamaan gerak C.
• Jika frekuensi tidak masuk resonansi, partikel C nyata tidak akan muncul. Namun, gangguan sementara dapat terjadi di bidang C, contoh dari apa yang sering disebut "partikel virtual" C, di mana kasus kuanta A dan B dapat menghilang. Apa hasil dari gangguan seperti itu? Saya sebagian menggambarkan proses ini di akhir artikel, di bagian "ekor".

Ini adalah keadaan umum. Mari kita selidiki detailnya.

Apa artinya partikel, yaitu kuanta bidang A, B, dan C, berarti berada dalam resonansi atau tidak dalam resonansi? Perlu diingat bahwa energi kuantum terkait dengan frekuensinya karena persamaan E = h ν. Jadi kami menerjemahkan diskusi kami tentang gelombang menjadi diskusi tentang partikel.

Misalkan gelombang kita dalam bidang A dan B terdiri dari masing-masing satu kuantum. Kuanta ini tidak memiliki massa, karena A dan B memenuhi persamaan kelas 0. Lebih tepatnya, istilah linear dalam persamaan geraknya sama dengan persamaan kelas 0. Karena kuanta A dan B memiliki frekuensi yang sama, mereka memiliki energi yang sama, E = h ν. Karena momentum kuantum tanpa massa adalah p = E / c, kuanta A dan B akan memiliki momenta yang besarnya sama dengan h ν / c, tetapi berlawanan arah, karena salah satunya bergerak ke kiri dan yang lainnya ke kanan. Oleh karena itu:

• Total energi dari dua kuanta bersama adalah 2 jam
• Total momentum dari dua kuanta bersama-sama akan menjadi nol.

Karena energi dan momentum dilestarikan, energi total setelah tabrakan dua kuanta akan tetap sama dengan 2 jam, dan momen total akan tetap nol.

Dalam kasus gelombang, kita melihat bahwa karena persamaan untuk C berisi istilah bentuk AB, ada resonansi ketika frekuensi AB (bekerja sebagai gaya osilasi) bertepatan dengan frekuensi minimum C (bekerja seperti bola pada pegas). Kami menerjemahkan pernyataan ini ke dalam kuanta.

Frekuensi AB akan menjadi 2 ν, oleh karena itu energi produk A dan B, ketika gelombang A dan B terdiri dari satu kuantum, sama dengan jumlah energi A dan B.

$$

$$E_ {AB} = 2 h \ nu = E_A + E_B$$

Frekuensi minimum C sama dengan ν _min , yang berarti bahwa untuk kuantum stasioner bidang C, momentumnya adalah 0, dan energi

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

Di mana m adalah massa kuantum C.

Untuk resonansi, 2 ν = ν _min diperlukan, yaitu:

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

Singkatnya, resonansi terjadi ketika jumlah energi yang sama dari partikel A dan B (di mana dalam kasus kami pulsa adalah sama besarnya dan berlawanan arah) hanya cukup untuk membuat partikel stasioner C! Dalam prosesnya, partikel A dan B dimusnahkan - energinya sepenuhnya digunakan untuk menciptakan partikel C. Ini ditunjukkan (secara skematis) pada Gambar. 2, yang perlu Anda bandingkan dengan ara. 1.


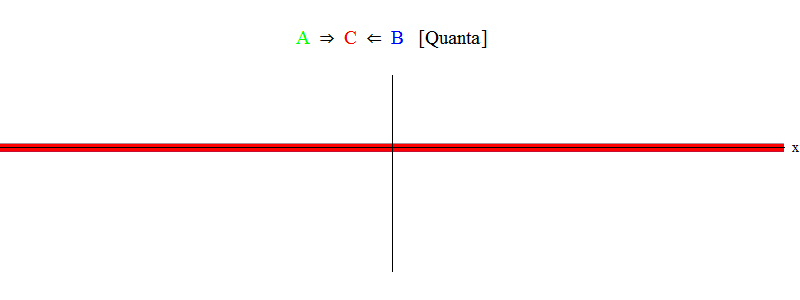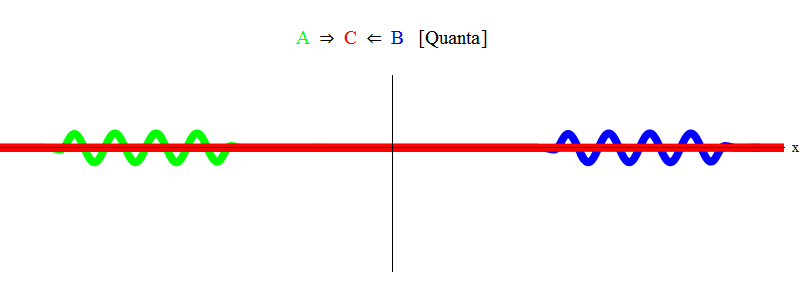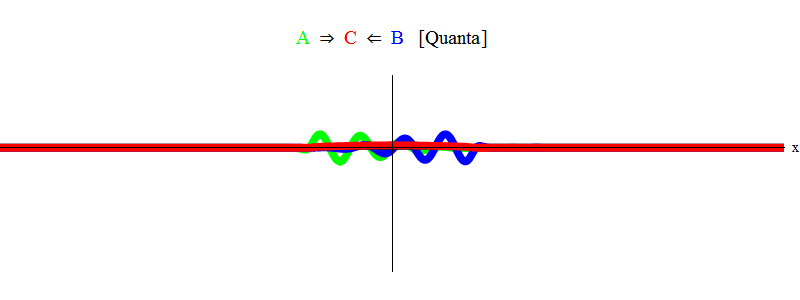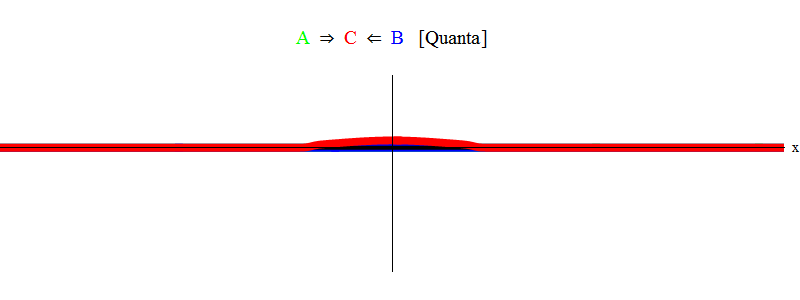Fig. 2

Alasan

Saya baru saja menunjukkan kepada Anda proses A + B → C. Dalam penjelasan saya, saya menggunakan tiga jenis partikel yang berbeda untuk menghindari kebingungan. Tetapi ide yang sama memungkinkan seseorang untuk melalui proses dari bentuk A + A → C (misalnya, gluon + gluon → partikel Higgs, dan pada dasarnya ini adalah bagaimana partikel Higgs diperoleh dalam Large Hadron Collider) dan proses dari bentuk A + A * → C, di mana A * - antipartikel untuk A (misalnya, quark + antiquark → Z-partikel, dan ini adalah bagaimana Z-partikel biasanya diperoleh pada LHC). Anda hanya perlu mengubah detail kecil, tetapi esensinya tetap sama.

Proses lain yang mewakili ide yang sama, hanya terbalik dalam waktu - pembusukan partikel. Peluruhan partikel Higgs menjadi dua foton atau partikel Z menjadi quark dan antiquark pada dasarnya terjadi sebagai animasi pada Gambar. 2, pergi ke arah yang berlawanan.

Ekor

1. Jika istilah AB mengganggu bidang C tanpa resonansi - jika 2 ν ≠ ν _min - apa yang akan terjadi? Anda mungkin ingat bahwa jika Anda mendorong ayunan dengan anak pada frekuensi yang salah, atau menerapkan gaya pada bola pada pegas, berosilasi dengan frekuensi yang tidak sesuai dengan frekuensi alami getaran, Anda akan mendapatkan getaran yang tidak merata dengan amplitudo kecil. Dalam konteks saat ini, hal yang sama terjadi dengan bidang C. Bidang C entah bagaimana akan berperilaku, tetapi ini tidak akan mengarah pada munculnya kuantum berperilaku baik C. Itu hanya mendapat sedikit khawatir. Kemarahan buruk ini adalah salah satu contoh dari apa yang disebut "Partikel virtual C" - tetapi ini bukan partikel (kuantum gelombang medan C), terlepas dari namanya. Massanya berbeda dari massa partikel C; bisa lebih besar atau lebih kecil. Tidak seperti partikel C, itu tidak ada dengan sendirinya untuk waktu yang lama. Dan itu tidak memenuhi kondisi amplitudo yang harus dipenuhi oleh kuanta nyata. Sebaliknya, tidak seperti partikel C, yang ada selama beberapa waktu, dengan ara. 2, gangguan nonresonan hanya ada ketika A memotong B.

Tetapi ini tidak berarti bahwa itu tidak mempengaruhi apa pun. Sebagai contoh, ini dapat menyebabkan partikel A dan B saling memantul.

$$

$$A_ \ rightarrow + B_ \ leftarrow → C_ {outrage} → A_ \ leftarrow + B_ \ rightarrow$$

Secara umum, dalam ruang tiga dimensi, pantulan, atau hamburan, dapat mengarah pada fakta bahwa A bergerak ke segala arah dan B bergerak ke arah yang berlawanan. Contoh dari proses tersebut termasuk hamburan elektron dan positron karena foton virtual, atau hamburan quark dan antiquark karena gluon virtual.

Di hadapan bidang lain, D dan E, berinteraksi dengan C dan berpartisipasi dalam persamaan gerak C

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B + y D D E$$

Proses yang jauh lebih menarik dapat terjadi:

A + B → G _gangguan → D + E

Itu benar: partikel A dan B dapat memusnahkan berkat partikel virtual C, dan menyebabkan munculnya partikel baru D dan E. Ini adalah cara kedua untuk membuat partikel baru! Sebagai contoh, sebuah elektron dapat bertabrakan dengan positron, musnahkan melalui foton virtual (ingat bahwa ini berarti "melalui perturbasi bidang foton pada frekuensi yang tidak bertepatan dengan resonansi"), dan berubah menjadi muon dan antimuon, atau quark dan antiquark. Quark yang lebih rendah dan antiquark atas dapat bertabrakan, dimusnahkan melalui partikel-W virtual, dan berubah menjadi elektron dan antineutrino. Atau dua gluon dapat bertabrakan, dimusnahkan melalui virtual gluon, dan berubah menjadi quark atas dan antiquark atas (ini adalah cara paling umum untuk mendapatkan quark atas pada LHC).

2. Bagaimana jika dua gelombang dalam bidang A dan B memiliki frekuensi yang berbeda, ν _A dan ν _B ? Pada frekuensi yang sesuai, partikel C mungkin masih muncul, tetapi kondisi resonansi akan berbeda, dan partikel C yang dibuat tidak akan diam. Mari kita cari tahu.

Jika mereka memiliki frekuensi yang berbeda, maka dua quanta yang tidak bertabrakan akan memilikinya

• Berbagai energi $$$E_A = h \ nu_A$ dan $$$E_B = h \ nu_B$
• Berbagai impuls $$$p_A = + h \ nu_A / c$ dan $$$p_B = - h \ nu_B / c$ (di sini, plus berarti ke kanan, minus ke kiri).

Total momentum p _A + p _B sekarang bukan nol. Namun momentum itu tetap ada. Oleh karena itu, jika partikel C dapat terjadi sebagai akibat pemusnahan partikel A dan B, ia akan memiliki momentum p _C = p _A + p _B , sehingga akan bergerak ke kiri atau ke kanan, dan tidak diam. Jika ν _A > ν _B , maka ia akan bergerak ke kanan, jika tidak, ke kiri.

Berapa banyak energi yang dibutuhkan untuk membuat partikel C yang bergerak? Untuk ini, lebih banyak energi diperlukan daripada untuk yang diam - seperti partikel masif apa pun, energi dan momentumnya harus memuaskan

$$

$$E_C ^ 2 = (p_Cc) ^ 2 + (mc ^ 2) ^ 2$$

Yang berarti bahwa E _C = mc ² jika p _C = 0, atau lebih jika momentumnya bukan nol. Hukum kekekalan energi dan momentum memberi tahu kita bahwa:

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c - E_B / c$$

Di mana saya mendapatkan persamaan terakhir? Untuk partikel tanpa massa, p = E / c, dan untuk partikel bertabrakan A dan B, momentumnya berlawanan, sehingga mereka berbeda dalam pertanda. Ganti ini dalam persamaan sebelumnya dan dapatkan:

$$

$$(E_A + E_B) ^ 2 = (E_A - E_B) ^ 2 + (mc ^ 2) ^ 2$$

Istilah E _A ² dan E _B ² saling dimusnahkan, dan memindahkan istilah E _A E _B ke kiri, kita dapatkan:

$$

$$4 E_A E_B = (mc ^ 2) ^ 2$$

Dibagi dengan h ² dan menggunakan relasi m = hν _min / c ² , kita memperoleh kondisi resonansi:

$$

$$(2 \ nu A) (2 \ nu B) = \ nu_ {min} ^ 2$$

Yang mengurangi dengan benar ketika ν _A = ν _B ke persamaan untuk partikel C yang tidak bergerak, 2 ν = ν _min . Jika kondisi ini tidak dipenuhi, maka partikel C tidak dapat dibuat. Jika puas, maka itu mungkin.

3. Saya mencatat bahwa dengan cara yang sama seperti persamaan gerak untuk bidang C berisi istilah AB, sehingga persamaan untuk B berisi istilah AC. Ingat persamaan ini:

$$

$$d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y A C$$

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Jadi, jika superposisi gelombang A dan B mengarah ke penampilan gelombang di bidang C, menjadikannya nol, seperti pada Gambar. 1, apakah kita perlu khawatir tentang fakta bahwa gelombang C baru ini tumpang tindih dengan gelombang A yang ada dan mengarah ke perubahan di bidang B? Saya menjawab bahwa "ya, tapi kita bisa mengabaikan ini." Kita dapat mengabaikan karena kombinasi dari dua alasan.

Pertama, karena angka "y" muncul sebelum penggandaan AB dan BC. Dampak pada bidang C dari anggota AB sebanding dengan y kali A dikalikan dengan B. Dampak pada bidang B dari anggota AC juga sebanding dengan y kali A dikalikan dengan C, tetapi ini pada gilirannya akan sama dengan y ² kali A dikalikan dengan oleh A dikalikan dengan B. Jadi selama y kurang dari 1, y ² akan lebih kecil dari y, oleh karena itu, efek pada B dari anggota AC kecil dibandingkan dengan efek pada C dari anggota AB - setidaknya untuk gelombang kecil A dan B. Dalam praktiknya, ini gelombang biasanya kecil: partikel A adalah satu kuantum dari gelombang di bidang A, oleh karena itu, gelombang A memiliki amplitudo kecil d.

Yang diikuti oleh alasan kedua, orang asing, tetapi lebih meyakinkan: kita melihat bahwa jika satu kuantum A memenuhi satu kuantum B dan berubah menjadi satu kuantum C, maka gelombang A dan B menghilang (musnahkan). Setelah pembuatan C, tidak ada lagi gelombang A, oleh karena itu AC nol, yaitu, tidak ada efek pada bidang B.

Dan tangkapan terakhir: meskipun saya tidak dapat membuktikan ini tanpa perhitungan tambahan, bahkan jika gelombang A dan B terdiri dari satu kuantum, seperti pada Gambar. 2, lalu proses pada Gbr. 2 akan jauh lebih rumit jika y jauh lebih besar dari 1. Jadi kesederhanaan cerita yang saya ceritakan membutuhkan nilai-nilai kecil y. Di alam, mayoritas istilah nonlinier dalam fisika partikel biasanya kecil, jadi apa yang saya katakan berlaku untuk situasi yang paling praktis berlaku. Pengecualiannya sangat menarik - mereka mengarah pada penciptaan objek kompleks seperti proton dan hadron lainnya.