
Fisika adalah ilmu kompleks yang paling kompleks, sama rumitnya, begitu menarik. Jika kita membuang komponen matematika, fisika segera menjadi tersedia bagi siapa saja dengan rasa ingin tahu dan imajinasi. Kita akan dengan mudah memahami konsep teori gravitasi, mengeluarkan persamaan matematika yang kompleks. Karena itu, untuk semua orang yang berpikir tentang apa yang membuat blueberry biru dan stroberi merah; siapa yang meragukan suara itu merambat dalam bentuk gelombang; ada yang bertanya-tanya mengapa perilaku cahaya sangat berbeda dari fenomena lain di alam semesta, Anda perlu memahami bahwa semuanya ada dalam fisika kuantum.
Buku ini menyajikan (dan menghilangkan mitos) bagi orang awam dunia magis sains kuantum, tidak seperti buku lainnya. Dia berbicara tentang konsep dasar ilmiah, dari partikel cahaya ke keadaan materi dan penyebab dampak negatif gas rumah kaca, mengungkapkan setiap topik tanpa menggunakan terminologi ilmiah tertentu - contoh dari kehidupan sehari-hari biasa. Tentu saja, sebuah buku tentang fisika kuantum tidak dapat melakukan tanpa set rumus dan persamaan minimum, tetapi ini adalah minimum yang diperlukan, dapat dimengerti oleh sebagian besar pembaca. Menurut penulis, buku yang mempopulerkan sains harus dapat diakses, tetapi tidak lebih rendah ke tingkat pembaca, tetapi untuk meningkatkan dan mengembangkan kecerdasan dan tingkat budaya umum.
Racquetball Quantum dan Warna Buah
Properti kunci dari elektron yang terikat pada atom dan molekul adalah bahwa status energinya berbeda. Kami mengatakan bahwa energi suatu elektron dapat dikuantisasi, yaitu, elektron yang terikat pada atom atau molekul hanya dapat memiliki beberapa nilai energi tertentu. Energi berubah bertahap, dan langkah-langkah ini memiliki ukuran diskrit tertentu. Keadaan energi seperti tangga. Anda bisa berdiri di satu langkah atau naik ke langkah berikutnya yang lebih tinggi. Namun, tidak mungkin untuk berdiri di antara dua langkah. Nilai-nilai energi yang terpisah, atau terkuantifikasi, ini sering disebut tingkat energi. Tidak seperti tangga biasa, interval antara tingkat energi biasanya tidak sama.
Bidang penting dari penelitian kuantum modern adalah perhitungan keadaan elektronik molekul. Area ini disebut kimia kuantum. Perhitungan semacam itu memungkinkan untuk memperoleh tingkat energi yang dikuantisasi untuk elektron dalam molekul (tingkat energi), serta untuk menghitung struktur molekul. Perhitungan struktur molekul memberikan jarak antara atom dan posisi semua atom dalam molekul dengan akurasi hanya dibatasi oleh prinsip ketidakpastian. Dengan demikian, perhitungan mekanika kuantum memungkinkan untuk menentukan ukuran dan bentuk molekul. Perhitungan semacam itu penting untuk memahami prinsip-prinsip dasar pengikatan atom pada molekul dan untuk konstruksi molekul baru. Dengan perkembangan teori kuantum dan munculnya komputer yang semakin kuat dan kompleks yang mampu memecahkan masalah matematika yang melelahkan, semakin banyak molekul besar dapat dipelajari menggunakan metode kimia kuantum. Salah satu aplikasi paling penting dari teori kuantum adalah pengembangan obat-obatan. Molekul dapat dirancang sedemikian rupa sehingga memiliki ukuran dan bentuk yang sesuai dengan lokus protein atau enzim tertentu.
Kimia kuantum membutuhkan perhitungan yang sangat melelahkan. Bahkan untuk atom hidrogen yang paling sederhana, perhitungan mekanika kuantum secara matematis sangat rumit. Atom hidrogen terdiri dari satu elektron yang terikat pada satu proton. Proton, yang merupakan inti atom hidrogen, adalah partikel bermuatan positif, dan elektron bermuatan negatif. Daya tarik elektron bermuatan negatif ke proton bermuatan positif menyatukan mereka, menyatukan atom hidrogen. Rincian perhitungan tingkat energi atom hidrogen tidak akan disajikan di sini, tetapi dalam bab-bab berikut kami akan mempertimbangkan beberapa fitur dari hasil perhitungan ini. Mereka memberikan tingkat energi atom hidrogen dan fungsi gelombangnya. Ini adalah fungsi gelombang, yaitu gelombang amplitudo probabilitas untuk atom hidrogen, yang merupakan titik awal untuk memahami semua atom dan molekul. Atom dan molekul adalah kompleks karena mereka benar-benar kecil sistem tiga dimensi, dan perlu untuk mempertimbangkan bagaimana proton dan elektron berinteraksi satu sama lain.
Partikel dalam kotak - kasing klasik
Ada tugas yang sangat sederhana terkait dengan topik kita. Ini dikenal sebagai masalah partikel dalam sebuah kotak. Ini tidak memerlukan matematika yang rumit untuk menyelesaikannya, tetapi solusi ini memungkinkan kita untuk menggambarkan sifat-sifat penting dari elektron yang terikat, misalnya, kuantisasi tingkat energi dan sifat gelombang seperti elektron di negara-negara terikat. Sebelum menganalisis sifat elektron dalam kotak ukuran atom satu dimensi, kita membahas masalah klasik taman bermain satu dimensi yang ideal untuk raket untuk mengidentifikasi perbedaan antara sistem klasik (besar) dan mekanika-kuantum (sangat kecil).
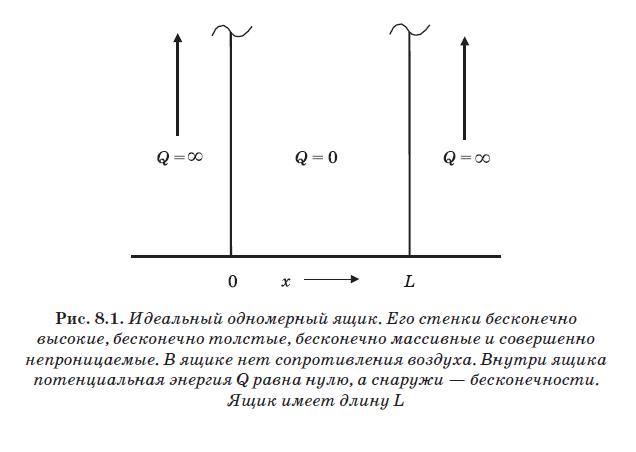
Dalam gbr. 8.1 menggambarkan "kotak" yang sempurna. Dia satu dimensi. Dindingnya dianggap sangat tinggi, sangat besar dan sangat tidak bisa ditembus. Tidak ada udara di dalam kotak untuk menahan gerakan. Dalam gambar, bagian dalam kotak ini ditunjuk Q = 0, dan bagian luar - Q = ∞. Dikatakan sebelumnya bahwa sebuah partikel disebut bebas sehingga tidak ada gaya yang bekerja padanya. Kekuatan muncul ketika sebuah partikel berinteraksi dengan sesuatu. Misalnya, partikel bermuatan negatif, seperti elektron, dapat berinteraksi dengan proton bermuatan positif. Interaksi dalam bentuk tarikan antara partikel bermuatan berlawanan akan menghasilkan gaya yang bekerja pada elektron. Saat mengendalikan elektron dalam CRT (lihat Gambar 7.3), medan listrik menghasilkan gaya yang bekerja pada elektron dan memaksa mereka untuk mengubah arah.
Ukuran interaksi partikel dengan sesuatu yang mempengaruhinya, seperti medan listrik, disebut potensial dan memiliki dimensi energi. Di masa depan, potensi akan dilambangkan dengan huruf Q. Di dalam kotak, Q = 0, seperti dalam kasus partikel bebas. Ini berarti bahwa partikel tidak berinteraksi dengan apa pun di dalam kotak. Tidak ada medan listrik atau hambatan udara. Namun, di luar kotak, Q = ∞. Potensi tak terhingga berarti suatu partikel harus memiliki energi tak terbatas agar berada di area di luar kotak. Ekspresi Q = ∞ hanyalah cara memformalkan pernyataan bahwa dinding kotak ideal. Sebuah partikel tidak dapat menembus dinding atau melompati mereka, tidak peduli seberapa besar energinya. Jika Anda menempatkan partikel di dalam kotak seperti itu, ia tidak bisa lepas dan akan selalu tetap di dalamnya. Dalam pengertian ini, partikel dikunci dalam sebuah kotak. Itu bisa berada di wilayah dengan panjang L, tapi tidak di tempat lain.
Dalam gbr. Gambar 8.2 menunjukkan bola untuk bermain bola raket, memantul dari dinding lapangan raket klasik satu dimensi (besar) yang ideal. Seperti yang telah disebutkan, dinding ini ideal, tetapi tidak ada hambatan udara di dalamnya. Selain itu, bola juga ideal, yaitu memiliki elastisitas absolut. Ketika bola bertabrakan dengan dinding, ia berkontraksi seperti pegas dan meluruskan lagi, menyebabkan bola memantul. Bola sungguhan tidak elastis sempurna. Ketika bola dikompresi karena tumbukan, tidak semua energi yang dikeluarkan untuk mengompresnya dihalau dari dinding. Bagian dari energi yang dihabiskan untuk mengompres bola digunakan untuk memanaskannya. Namun, di sini kita akan menganggap bola sangat elastis. Saat mengenai dinding, semua energi kinetik bola, yang menyebabkannya terkompresi, kemudian dihabiskan untuk mendorong bola menjauh dari dinding. Oleh karena itu, kecepatan bola tepat sebelum tumbukan dengan dinding sama dengan kecepatan rebound setelah tumbukan.
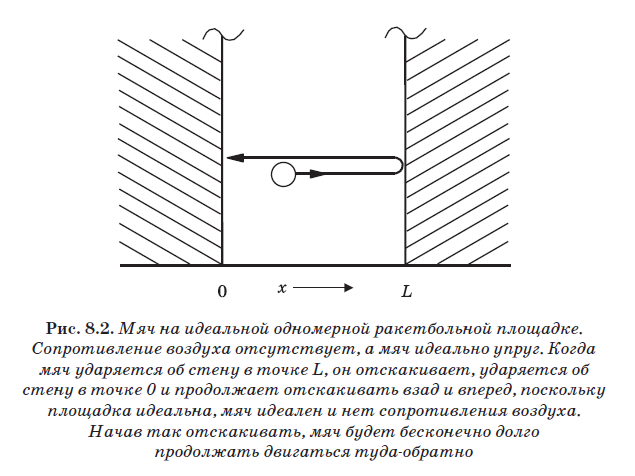
Di tanah bola raket yang ideal ini, bola memantul ke dinding tanpa kehilangan energi; selain itu, tidak ada hambatan udara atau gravitasi. Karena itu, bola akan selalu bergerak bolak-balik, memantulkan dinding. Itu mengenai dinding di titik L, terpental, bertabrakan dengan dinding di titik 0, terpental lagi dan terus bergerak bolak-balik. Di dalam kotak, karena potensinya nol (lihat Gambar 8.1), tidak ada gaya yang bekerja pada bola. Karena itu, energinya murni kinetik:
di mana m adalah massa bola, dan V adalah kecepatannya. Jika bola mengalami pengaruh eksternal yang lemah, kecepatannya akan menjadi sedikit lebih rendah dan nilai Ek juga akan sedikit menurun. Dalam bola raket yang ideal ini, energi dapat berubah secara terus-menerus. Nilai Ek dapat naik atau turun secara sewenang-wenang hanya bergantung pada kekuatan dampak pada bola.
Fitur penting lainnya dari raket klasik adalah kemampuan untuk menghentikan bola sehingga tidak bergerak di lantai. Dalam situasi ini, kecepatannya adalah nol: V = 0. Dan karena V = 0, lalu Ek = 0. Pada V = 0, momentumnya juga nol, karena p = mV, jadi kita tahu persis momentumnya. Jika bola terletak di lantai (V = 0), maka posisinya diketahui. Jika kita menyatakan posisi ini x (lihat Gambar 8.2), maka nilai x akan berada dalam kisaran dari 0 hingga L. Nilai x tidak dapat mengambil nilai lain, karena bola ada di lapangan (dalam kotak) dan tidak bisa berada di luar dari untuk dinding yang sempurna. Bola dapat ditempatkan di posisi tertentu x di lantai lapangan, dan kemudian posisinya akan diketahui dengan pasti. Ini adalah properti dari taman bermain makroskopik, bahkan ideal. Ini adalah sistem klasik, dan di dalamnya orang dapat secara tepat dan simultan mengetahui momentum p dan posisi x.
Lapangan racquetball memiliki panjang 12 m, diameter bola adalah 5,6 cm, dan beratnya sekitar 0,04 kg. Jelas, permainan racquetball dijelaskan oleh mekanik klasik. Dengan bantuan cahaya, Anda dapat mengikuti pantulan bola bolak-balik tanpa memengaruhi mereka.
Partikel dalam Kotak - Kasus Quantum
Apa yang akan berubah jika kita sekarang beralih ke pertimbangan quantum racquetball? Situs ini tetap ideal, tetapi sekarang panjangnya bukan 12 m, tetapi 1 nm (10–9 m). Selain itu, partikel memiliki massa elektron 9,1 10–31 kg, dan tidak 0,04 kg. Jadi, ini adalah masalah partikel kuantum dalam sebuah kotak.
Kita dapat langsung mengatakan bahwa energi terkecil dari partikel kuantum dalam kotak berukuran nanometer tidak boleh nol. Pada bidang bola raket klasik, kecepatan bola V dimungkinkan, yang sama dengan nol, yang berarti bahwa p = mV impuls bisa nol. Selain itu, posisi bola x memiliki makna yang jelas. Sebagai contoh, bola mungkin masih berbaring (V = 0) tepat di tengah lapangan, yang sesuai dengan x = L / 2. Dalam hal ini, untuk raket klasik kami, ∆p = 0 dan ∆x = 0. Nilai produk ∆x∆p = 0 tidak sesuai dengan prinsip ketidakpastian Heisenberg, yang normal, karena kita berbicara tentang sistem klasik. Namun, partikel yang sangat kecil dalam kotak berukuran nanometer adalah objek kuantum dan harus mematuhi prinsip ketidakpastian, yang menyatakan bahwa ∆x∆p ≥ h / 4. Jika V = 0 dan x = L / 2, maka kita tahu x dan p, yang berarti bahwa ∆x∆p = 0, seperti pada racquetball klasik. Untuk sistem kuantum, ini tidak mungkin. Jadi, V tidak bisa sama dengan nol. Sebuah partikel tidak bisa tetap bergerak pada titik tertentu. Dan jika nilai V adalah nol, maka nilai Ek tidak boleh sama dengan nol. Prinsip ketidakpastian mengatakan bahwa energi terkecil dari raket quantum kita tidak boleh nol. Sebuah bola kuantum tidak pernah bergerak.
Nilai energi partikel kuantum dalam sebuah kotak
Energi apa yang dapat dimiliki partikel kuantum dalam kotak berukuran nanometer? Pertanyaan ini dapat dijawab tanpa perhitungan yang rumit, tetapi pertama-tama kita harus kembali ke ombak lagi. Dalam bab 6 kita berbicara tentang fungsi gelombang dari partikel bebas. Fungsi gelombang partikel bebas dengan momentum spesifik p adalah gelombang yang memanjang ke seluruh ruang. Jadi, sebuah elektron dengan momentum yang terdefinisi dengan sempurna adalah gelombang yang terdelokalisasi, menutupi seluruh ruang. Probabilitas mendeteksi elektron bebas adalah sama di mana-mana. Elektron semacam itu memiliki energi kinetik yang didefinisikan dengan baik, Ek = 1 / 2mV2, karena ia memiliki momentum yang didefinisikan dengan baik p = mV.
Elektron dalam kotak nanometer mirip dengan partikel bebas kita sehubungan dengan wilayah bagian dalam kotak, di mana Q = 0. Tidak ada potensi di dalam kotak, dan karena itu tidak ada gaya yang bekerja pada partikel. Dalam hal ini, ia sangat mirip dengan partikel bebas, di mana tidak ada gaya yang bekerja juga. Namun, ada perbedaan penting antara partikel dalam kotak dan partikel bebas - ini adalah dinding kotak. Elektron di dalam kotak hanya di dalam kotak. Sifat ideal kotak tidak memungkinkan fungsi gelombangnya menyebar ke semua ruang. Partikelnya ada di dalam kotak dan tidak akan pernah ada di luar. Fungsi gelombang mengatur amplitudo probabilitas mendeteksi partikel di wilayah ruang tertentu. Ini adalah interpretasi Born dari fungsi gelombang. Jika elektron kita dapat dideteksi hanya di dalam kotak dan tidak pernah di luar, maka probabilitas pendeteksiannya di dalam kotak harus terbatas, dan di luar - nol. Jika probabilitas menemukan partikel di luar kotak adalah nol, maka fungsi gelombang harus nol pada semua titik di luar kotak.
Jadi, kita sampai pada kesimpulan bahwa fungsi gelombang dari suatu partikel dalam sebuah kotak mirip dengan fungsi gelombang dari partikel bebas, tetapi fungsi gelombang harus nol di luar kotak. Dalam interpretasinya tentang sifat fungsi gelombang kuantum-mekanis, Born memberlakukan beberapa pembatasan fisik pada bentuk yang dapat diambil fungsi gelombang. Salah satunya adalah fungsi gelombang yang baik harus kontinu. Kondisi ini berarti bahwa fungsi gelombang harus berubah dengan lancar dari satu tempat ke tempat lain. Perubahan posisi yang sangat kecil tidak dapat menyebabkan lompatan probabilitas yang tidak terduga. Ini adalah pemikiran yang sangat sederhana. Jika probabilitas mendeteksi partikel di wilayah yang sangat kecil adalah, misalnya, 1%, maka perpindahan nilai yang sangat kecil tidak dapat tiba-tiba tidak dapat secara tiba-tiba membuat probabilitas mendeteksi partikel sebesar 50%. Ini jelas dari gambar paket gelombang pada Gambar. 6.7. Probabilitas bervariasi dengan lancar dari satu tempat ke tempat lain. Ini memungkinkan kita untuk menambahkan sesuatu ke deskripsi fungsi gelombang suatu partikel dalam sebuah kotak, di samping fakta bahwa mereka adalah gelombang dengan amplitudo terbatas di dalam kotak dan amplitudo nol di luar. Karena fungsi gelombang harus kontinu, ia harus memiliki amplitudo nol langsung di dinding kotak dari dalam untuk bertepatan dengan amplitudo nol fungsi gelombang di luar kotak.
Dalam gbr. Gambar 8.3 menunjukkan diskontinuitas (dilarang) fungsi gelombang di dalam kotak. Fungsi gelombang ditunjukkan (huruf Yunani "fi"). Sumbu vertikal mewakili amplitudo fungsi gelombang. Garis putus-putus menunjukkan level nolnya. Fungsi gelombang, yang merupakan gelombang dari probabilitas amplitudo, dapat berfluktuasi antara nilai positif dan negatif. Fungsi gelombang ditunjukkan pada Gambar. 8.3, memiliki nilai di dekat dinding selain 0. Namun, fungsi gelombang harus nol di luar kotak, yaitu untuk nilai x kurang dari 0 dan lebih dari L, harus nol. Dalam gambar, fungsi gelombang tiba-tiba melompat dari nilai bukan nol di dekat dinding di dalam kotak ke nilai nol tepat di belakang dinding di luar kotak. Dengan demikian, fungsi gelombang ditunjukkan pada Gambar. 8.3 tidak valid karena tidak kontinu. Fungsi ini tidak bisa mewakili partikel kuantum dalam sebuah kotak.
Fungsi gelombang harus memiliki nilai nol di dinding
Agar fungsi gelombang yang mewakili partikel dalam kotak dapat diterima secara fisik, nilai-nilainya di dinding harus nol, dan kemudian mereka tidak akan mengalami celah di dinding. Tidak sulit untuk memenuhi kondisi ini. Fungsi gelombang berfluktuasi antara nilai positif dan negatif. Setiap kali, beralih dari nilai positif ke negatif atau dari negatif ke positif, ia melewati nol. Bahkan, titik nol dipisahkan satu sama lain dengan setengah panjang gelombang. Oleh karena itu, untuk mendapatkan fungsi gelombang yang baik dari sebuah partikel dalam sebuah kotak, kita harus memilih gelombang yang panjangnya memungkinkan mereka untuk ditumpuk di dalam kotak sehingga titik nol terletak tepat di dinding.
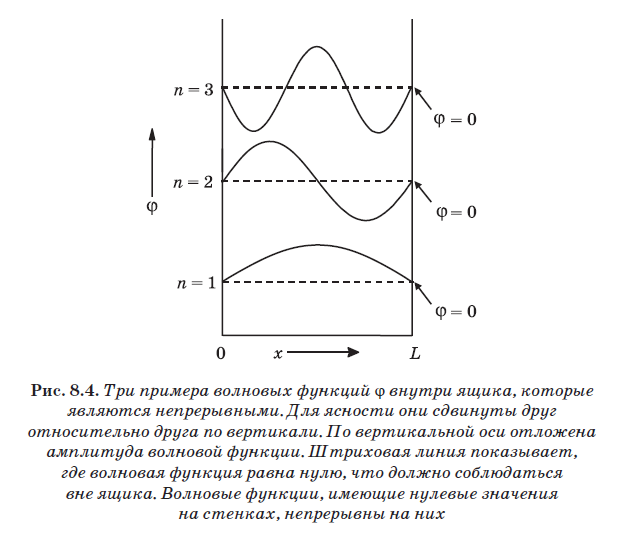
Dalam gbr. 8.4 menunjukkan tiga contoh gelombang yang cocok untuk peran fungsi gelombang untuk partikel dalam kotak. Yang lebih rendah dari mereka ditunjuk n = 1 dan terdiri dari satu setengah gelombang. Dimulai di sebelah kiri pada amplitudo 0, melewati maksimum dan kemudian kembali ke nol di dinding pada titik L. Gelombang berikutnya, yang terletak di atas dan ditandai n = 2, terdiri dari satu osilasi lengkap. Itu juga mulai di dinding kiri pada amplitudo 0, melewati puncak positif, kembali ke nol, lalu puncak negatif mengikuti dan kembali ke nol di dinding pada titik L. Gelombang yang ditunjukkan oleh n = 3 berisi satu setengah periode. Setiap gelombang yang mengandung bilangan bulat setengah-gelombang, yaitu, 1, 2, 3, 4, 5, dan seterusnya, setengah panjang gelombang, dan terletak sehingga dimulai dari nol di sebelah kiri dan berakhir di nol di sebelah kanan, cocok.
Nilai n adalah jumlah setengah gelombang dari fungsi gelombang tertentu. Untuk n = 1, panjang gelombang adalah 2L, karena panjang kotak adalah L, dan n = 1 sesuai dengan setengah panjang gelombang. Untuk n = 2, panjang gelombang adalah L, karena tepat satu panjang gelombang ditempatkan di antara dinding. Untuk n = 3, tiga setengah gelombang ditempatkan di antara dinding, yaitu 1,5 = L. Dalam hal ini = L / 1,5, yaitu = 2L / 3. Perhatikan bahwa aturan umum ditemukan di sini: = 2L / n, di mana n adalah bilangan bulat. Untuk n = 1 kita mendapatkan = 2L, untuk n = 2 - = 2L / 2, untuk n = 3 - = 2L / 3, dll.
»Informasi lebih lanjut tentang buku ini dapat ditemukan di
situs web penerbit»
Isi»
KutipanUntuk pembaca blog ini, diskon 20% untuk kupon -
Api