Bagaimana cara kerja bidang Higgs: 3) bagaimana partikel Higgs muncul

Bagaimana cara kerja bidang Higgs:

1. Ide utama
2. Mengapa bidang Higgs rata-rata bukan nol
3. Bagaimana partikel Higgs muncul
4. Mengapa bidang Higgs diperlukan

Dalam artikel sebelumnya, saya menjelaskan bagaimana dan mengapa bidang Higgs tidak memiliki nilai rata-rata nol. Sekarang saya ingin menggambarkan apa itu partikel Higgs dan bagaimana massanya muncul dari persamaan.

Saya ingin mengingatkan Anda bahwa jika kebalikannya tidak disebutkan, saya selalu menggambarkan bentuk paling sederhana dari bidang dan partikel Higgs - yang disebut Higgs Standard Model. Bentuk yang lebih kompleks juga dimungkinkan; misalnya, beberapa bidang Higgs mungkin ada secara bersamaan, bukan satu. Mungkin saya akan menjelaskan kasus yang lebih kompleks di salah satu artikel berikut.


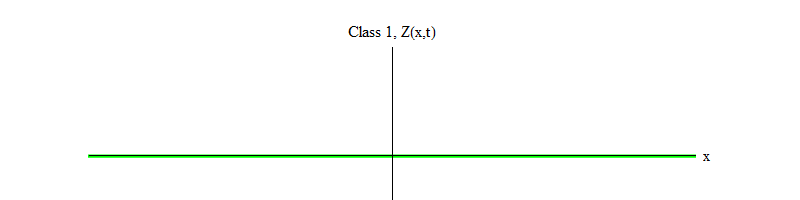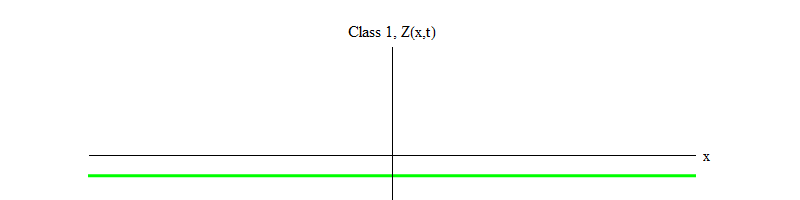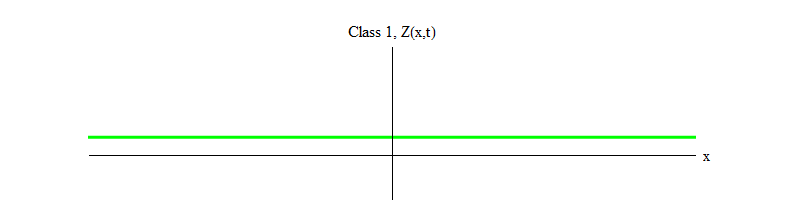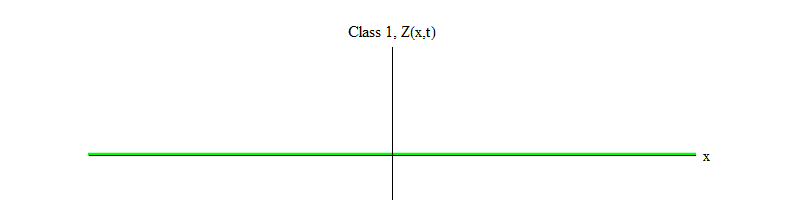Fig. 1: bidang kelas 1 berfluktuasi dalam waktu sekitar nilai yang stabil Z (x, t) = 0

Dalam artikel terakhir, saya tidak menekankan fakta ini, tetapi di antara bidang dasar yang kami temukan di alam, bidang Higgs unik. Semua bidang, kecuali Higgs, memenuhi persamaan gerak kelas 0 atau 1. Sebenarnya (meskipun ini mungkin tidak berlaku untuk semua bidang di alam), semua bidang yang kita tahu yang memenuhi persamaan kelas 1 melakukan ini karena bidang Higgs bukan nol . Jika nol, mereka semua akan memenuhi persamaan kelas 0 (seperti yang saya jelaskan di artikel pertama). Sebaliknya, bidang Higgs memenuhi persamaan yang dapat disebut persamaan kelas -1.

Untuk bidang Z (x, t), kelas yang saya definisikan terlihat seperti ini:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - B ^ 2 Z \ quad [Kelas 1 - masif \; partikel] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0 \ quad [Kelas 0 - tanpa massa \; partikel] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = + B ^ 2 Z \ quad [Kelas -1 - tidak stabil]$$

Persamaan menyiratkan bahwa B ² > 0.


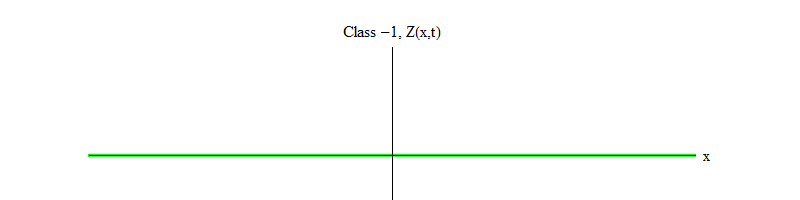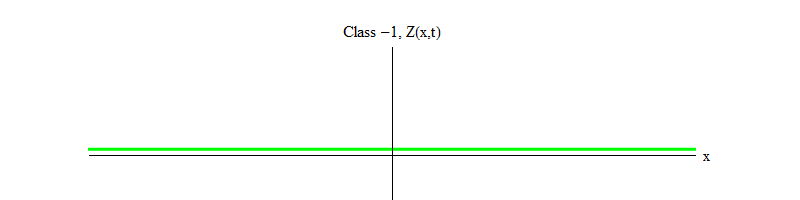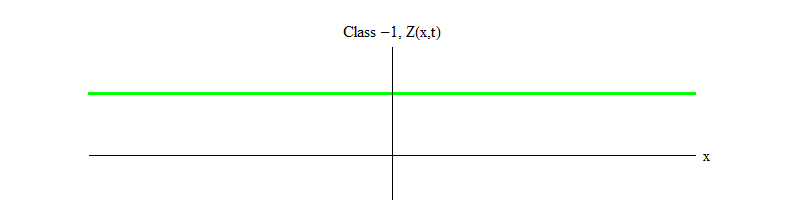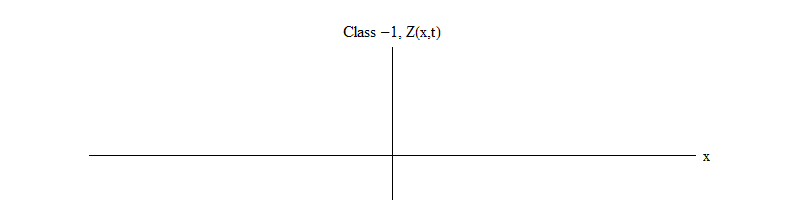Fig. 2: Bidang kelas -1 meninggalkan keseimbangan Z yang tidak stabil (x, t) = 0.

Tanda minus antara kelas 1 dan kelas -1 sangat penting. Dalam kedua kasus, solusi dari persamaan mengandung Z (x, t) = 0 sebagai salah satu kasus khusus, tetapi untuk kelas 1 Z (x, t) = 0 stabil, yaitu, Z (x, t) dapat berfluktuasi sekitar nol; ini adalah gelombang berperilaku sopan dengan kuantum masif. Dan sebaliknya, kelas -1 Z (x, t) = 0 tidak stabil, yaitu, Z (x, t) tidak akan berfluktuasi, tetapi tumbuh semakin banyak nilai. Jika Anda tidak mengubah persamaan, besarnya bidang akan terbang hingga tak terbatas. Lebih tepatnya, jika solusi untuk persamaan kelas 1 adalah osilasi Z, seperti pada Gambar. 1, solusi untuk persamaan kelas -1 adalah pertumbuhan eksponensial dari Z, seperti pada Gambar. 2.

Untuk bidang Higgs, serta untuk bidang apa pun yang ada di alam, persamaan kelas -1 diubah menggunakan istilah yang membatasi pertumbuhan eksponensial dan mencegah bidang agar tidak terbatas. Seperti yang kita lihat di artikel sebelumnya, bidang Higgs mematuhi persamaan gerak

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2) = + (bv) ^ 2 H - b ^ 2 H ^ 3$$

Itu milik kelas -1 ketika H hampir nol, tetapi memiliki anggota penting dari H ³ . Di sini b adalah bilangan positif, dan v adalah posisi keseimbangan untuk H. Persamaan ini memastikan bahwa jika bidang H dimulai pada titik H = 0 dan bergerak dari posisi kesetimbangan tidak stabil ke positif H, maka ia akan berosilasi di sekitar posisi keseimbangan stabil di H = v (gbr. 3).


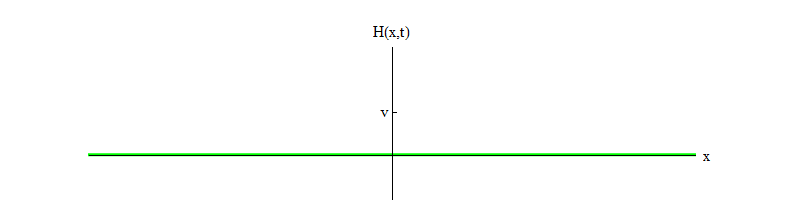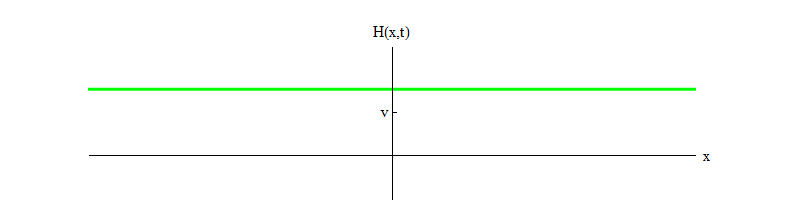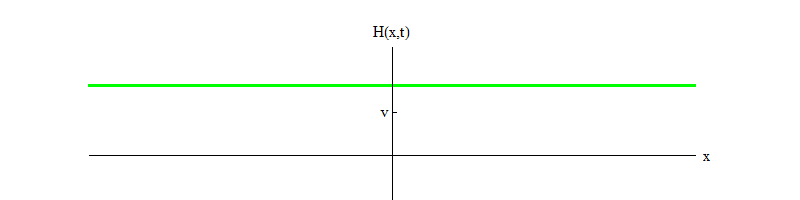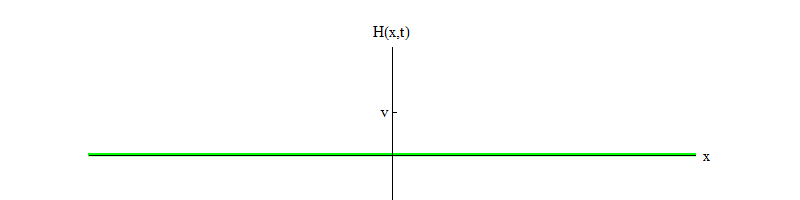Fig. 3

Seiring waktu, osilasi akan memudar, karena ketentuan persamaan gerak, yang saya hilangkan untuk singkatnya; mereka memungkinkan sebagian energi osilasi medan H ditransfer ke gelombang bidang lain (ini adalah istilah nonlinier yang sama yang memungkinkan partikel Higgs membusuk ). Seiring waktu (Gbr. 4), bidang H akan tenang di posisi H = v.


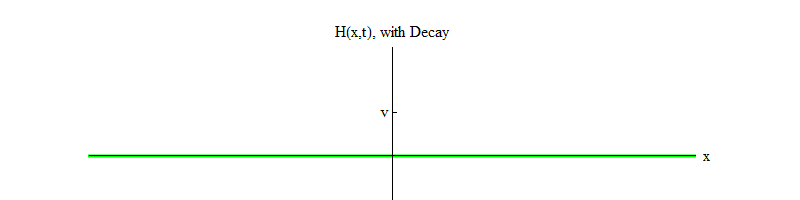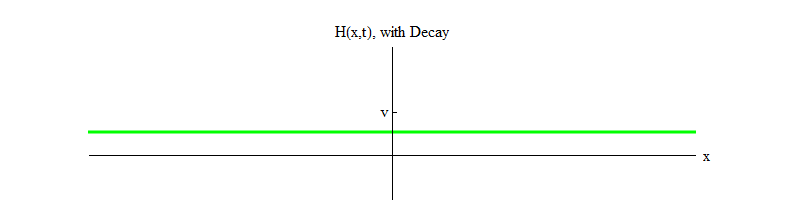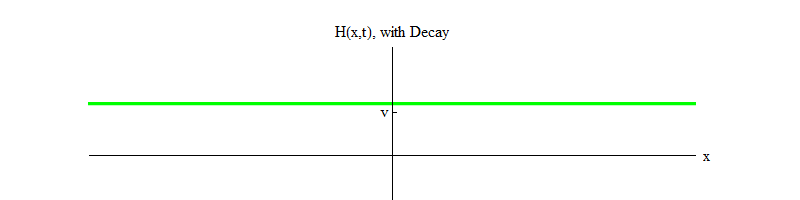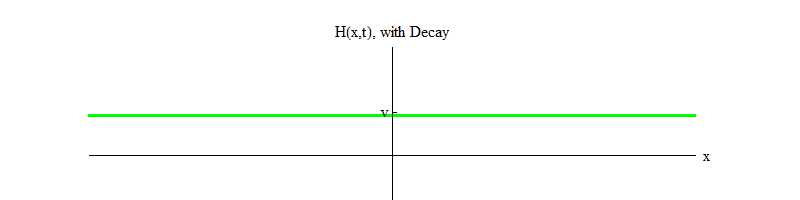Fig. 4

Jika ada proses fisik yang mengetuk bidang dari posisi H = v di wilayah kecil ruang, bidang tersebut akan memancarkan gelombang bentuk

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

Di mana A adalah amplitudo gelombang, ν dan λ adalah frekuensi dan panjang gelombangnya, dan hubungan antara ν dan λ tergantung pada bentuk persamaan gerak yang tepat, khususnya, pada b dan v. Dan kuanta dari gelombang ini adalah partikel Higgs. Pertanyaan per juta: berapakah massa partikel Higgs? Untuk menghitung ini, kita perlu, seperti yang selalu diperlukan untuk partikel (mewakili kuanta gelombang dalam bidang relativistik), menentukan hubungan antara frekuensi ν dan panjang gelombang λ dari gelombang bidang yang sesuai, dan kemudian mengalikan hasilnya dengan konstanta Planck h untuk mendapatkan rasio antara energi dan momentum kuantum dari gelombang ini, yang akan memberi tahu kita massa kuantum (mis., partikel).

Kami melakukan hal itu dengan bidang S (x, t) yang disebutkan dalam artikel pertama . Kami menulis versi bergeser dari bidang Higgs, menyatakannya sebagai H (x, t) = v + h (x, t) , dan menggantinya dengan persamaan gerak bidang H., (x, t) saya akan menulis dengan berani untuk membedakannya dari konstanta Planck h. Dalam contoh untuk bidang S yang diberikan dalam artikel ulasan, persamaan gerak yang sederhana ditunjukkan, sehingga perubahan tidak mengubah massa partikel S. Tetapi dalam kasus ini tidak! Persamaan gerak bidang Higgs lebih kompleks, sehingga persamaan untuk h sangat berbeda dari persamaan asli untuk H:

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - b ^ 2 (v + \ textbf {h}) (2 v \ textbf {h} + \ textbf {h} ^ 2)$$

Di mana saya menggunakan fakta bahwa v adalah konstanta dan tidak tergantung pada ruang dan waktu. Kemudian kita ingat bahwa kuantum medan Higgs memiliki amplitudo kecil, oleh karena itu, ketika mempelajari satu-satunya partikel Higgs (yang persis apa yang kita butuhkan untuk menentukan massanya), kita dapat membuang semua istilah yang proporsional dengan h ² dan h ³ :

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - 2 b ^ 2 v ^ 2 \ textbf {h} + ...$$

Di mana "+ ..." mengingatkan anggota yang dijatuhkan. Perhatikan bahwa persamaan untuk h (x, t) ini milik kelas 1, meskipun kami mulai dengan persamaan kelas -1 untuk H (x, t); ini karena H (x, t) tidak stabil di wilayah H = 0, dan h (x, t) stabil di wilayah h = 0, di mana H = v. Jadi kita bisa menghitung massa m _{h dari} partikel Higgs h menggunakan bentuk persamaan kelas 1 berikut:

$$

$$m_h = \ sqrt2 (h / 2 \ pi) b v / c ^ 2$$

h di sebelah kanan menunjukkan konstanta Planck. Jika partikel mirip-Higgs yang baru-baru ini ditemukan di LHC benar-benar berubah menjadi partikel Higgs dari Model Standar, maka untuk pertama kalinya kita dapat mengetahui apa b itu (ingat bahwa v kita sudah tahu sejak lama) dan, akhirnya, kita dapat mengetahui nilai a = b v.

• v = 246 GeV;
• m _h ≈ 125 GeV / c² (jika partikel baru adalah Higgs)
• b ≈ 0,35 (2 π / jam) (jika partikel baru adalah Higgs dari Model Standar)
• a = bv ≈ 87 GeV (2 π / h) (jika partikel baru adalah Higgs dari Model Standar)

di mana h, sekali lagi, adalah konstanta Planck. Dan tiga kuantitas terakhir tidak diketahui oleh kita sampai penemuan partikel Higgs baru-baru ini.

Sekarang, jika ternyata Model Standar tidak sesuai dengan alam (jika, selain H (x, t), perlu menambahkan bidang tambahan ke bidang yang diketahui untuk menjelaskan sifat-sifat partikel massa yang baru ditemukan 125 GeV / c²), mari kita asumsikan bahwa partikel ini adalah salah satu dari beberapa jenis partikel Higgs - maka kita harus menghadapi situasi sulit ini di LHC selama beberapa tahun lagi. Anda dapat membayangkan banyak kemungkinan, dan tidak ada gunanya menjelaskannya kepada Anda semua, tetapi secara kasar saya telah menjelaskan beberapa di antaranya; dan jika data yang diterima di LHC akan menunjukkan kepada kita arah tertentu, saya akan menjelaskan semuanya kepada Anda secara rinci.