Mekanika klasik bersifat intuitif: digunakan setiap hari dan berulang kali oleh manusia untuk bertahan hidup. Tetapi sampai abad kedua puluh, tidak ada yang pernah menggunakan mekanika kuantum. Dia menggambarkan hal-hal yang sangat kecil sehingga mereka sepenuhnya jatuh dari persepsi indera manusia. Satu-satunya cara untuk memahami teori ini, untuk menikmati keindahannya, adalah dengan memblokir intuisi kita dengan matematika abstrak.
Leonard Sasskind - seorang ilmuwan Amerika yang terkenal - mengundang Anda untuk melakukan perjalanan yang menyenangkan ke negara mekanika kuantum. Di perjalanan, Anda akan memerlukan pengetahuan dasar dari kursus fisika sekolah, serta dasar-dasar analisis matematika dan aljabar linier. Anda juga perlu mengetahui sesuatu tentang masalah-masalah yang dibahas dalam buku pertama Susskind tentang "teori minimum" - "Segala sesuatu yang perlu Anda ketahui tentang fisika modern." Tetapi tidak ada rasa takut jika pengetahuan ini agak dilupakan. Banyak penulis akan mengingatkan dan menjelaskan sepanjang jalan.
Mekanika kuantum adalah teori yang tidak biasa: menurut dalil-dalilnya, misalnya, kita dapat mengetahui segala sesuatu tentang sistem dan tidak mengenai bagian-bagian individualnya. Einstein dan Niels Bohr banyak berdebat tentang ini dan kontradiksi lainnya. Jika Anda tidak takut kesulitan, memiliki pikiran yang ingin tahu, secara teknis kompeten, tulus dan sangat tertarik pada fisika, maka kuliah ini oleh Leonard Sasskind akan menarik bagi Anda. Buku ini berfokus pada prinsip-prinsip logis dari teori kuantum dan bertujuan untuk tidak melancarkan paradoks logika kuantum, tetapi untuk menariknya ke dalam cahaya hari dan mencoba untuk berurusan dengan masalah-masalah sulit yang ditimbulkannya.
Ikhtisar Fungsi Gelombang
Dalam kuliah ini kita akan menggunakan bahasa fungsi gelombang, jadi mari kita lakukan tinjauan singkat tentang materi sebelum menyelam. Kami membahas dalam kuliah 5 fungsi gelombang objek abstrak, tanpa menjelaskan bagaimana mereka berhubungan dengan gelombang atau fungsi. Sebelum mengisi celah ini, saya mengingatkan Anda tentang apa yang kami bahas sebelumnya.
Untuk memulainya, kita memilih L yang dapat diamati dengan nilai eigen l dan vektor eigen | l〉. Biarkan | Y〉 menjadi vektor keadaan. Karena vektor eigen dari operator Hermitian membentuk basis ortonormal yang lengkap, vektor | Y〉 dapat diperluas dalam basis ini:
Seperti yang Anda ingat dari Bagian 5.1.2 dan 5.1.3, jumlah Y (l) disebut fungsi gelombang sistem. Tetapi perhatikan: bentuk spesifik Y (l) tergantung pada L yang dapat diamati spesifik yang awalnya kami pilih. Jika kita memilih yang lain yang dapat diamati, fungsi gelombang (bersama dengan basis vektor dan nilai eigen) akan berubah menjadi berbeda, meskipun faktanya kita masih berbicara tentang keadaan yang sama. Oleh karena itu, kita harus membuat reservasi bahwa Y (l) adalah fungsi gelombang yang terkait dengan | Yñ. Lebih tepatnya, kita harus mengatakan bahwa Y (l) adalah fungsi gelombang dalam basis-L. Jika kita menggunakan sifat ortonormalitas dari basis vektor 〈li | lj〉 = dij ini, maka fungsi gelombang dalam basis-L ini juga dapat didefinisikan menggunakan produk internal (atau proyeksi) dari vektor state | Y〉 pada vektor eigen | l〉: Y (l ) = 〈L | Y〉
Ada dua cara untuk memikirkan fungsi gelombang. Pertama-tama, ini adalah satu set komponen dari vektor keadaan secara spesifik. Komponen-komponen ini dapat ditulis dalam bentuk vektor kolom:
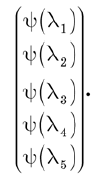
Cara lain untuk berpikir tentang fungsi gelombang adalah dengan menganggapnya sebagai fungsi l. Jika Anda menetapkan nilai l yang valid, maka fungsi Y (l) memberikan bilangan kompleks. Dengan demikian, kita dapat mengatakan bahwa Y (l) adalah fungsi bernilai kompleks dari variabel diskrit l. Dengan pertimbangan ini, operator linier menjadi operasi yang berlaku untuk fungsi dan memberikan fungsi baru.
Dan satu lagi pengingat terakhir: probabilitas bahwa percobaan akan memberikan hasil l sama dengan P (l) = Y * (l) Y (l).
Fungsi dan Vektor
Sampai sekarang, sistem yang kami pelajari memiliki vektor keadaan hingga. Sebagai contoh, putaran sederhana dijelaskan oleh ruang keadaan dua dimensi. Untuk alasan ini, yang dapat diobservasi hanya memiliki sejumlah terbatas dari nilai yang mungkin dapat diobservasi. Tetapi ada yang lebih kompleks yang dapat diamati yang dapat memiliki jumlah nilai yang tak terbatas. Contohnya adalah partikel. Koordinat partikel dapat diobservasi, tetapi tidak seperti putaran, koordinat memiliki jumlah kemungkinan nilai yang tak terbatas. Sebagai contoh, sebuah partikel yang bergerak di sepanjang sumbu x dapat berada pada tanda material apa pun x. Dengan kata lain, x adalah variabel tak terhingga yang berkelanjutan. Ketika sistem yang diamati kontinu, fungsi gelombang menjadi fungsi penuh dari variabel kontinu. Untuk menerapkan mekanika kuantum ke sistem semacam ini, kita harus memperluas konsep vektor sehingga mencakup fungsi di dalamnya.
Fungsi adalah fungsi, dan vektor adalah vektor; mereka tampaknya entitas yang sama sekali berbeda, jadi dalam arti apa vektor fungsi? Jika Anda menganggap vektor sebagai panah dalam ruang tiga dimensi, maka tentu saja vektor-vektor itu tidak sama dengan fungsi. Tetapi jika Anda melihat vektor lebih luas, seperti pada objek matematika yang memuaskan beberapa postulat, fungsi sebenarnya membentuk ruang vektor. Ruang vektor semacam itu sering disebut ruang Hilbert untuk menghormati ahli matematika David Hilbert.
Pertimbangkan himpunan fungsi kompleks Y (x) dari satu variabel nyata x. Dengan fungsi yang kompleks, maksud saya bahwa untuk setiap x itu mengaitkan bilangan kompleks Y (x). Variabel independen x, di sisi lain, adalah variabel riil biasa. Itu bisa mengambil nilai nyata dari –∞ hingga + ∞.
Sekarang kita menyatakan dengan tepat apa yang kita maksud dengan mengatakan bahwa "fungsi adalah vektor". Ini bukan analogi atau metafora yang dangkal. Di bawah beberapa batasan (yang akan kita bahas nanti), fungsi-fungsi seperti Y (x) memenuhi aksioma matematika yang mendefinisikan ruang vektor. Kami menyebutkan ide ini secara singkat di bagian 1.9.2, dan sekarang kami menggunakannya dengan kekuatan penuh. Melihat kembali aksioma ruang vektor yang kompleks (dalam Bagian 1.9.1), kita melihat bahwa fungsi kompleks memuaskan semuanya.
1. Jumlah dari dua fungsi adalah fungsi.
2. Penambahan fungsi bersifat komutatif.
3. Penambahan fungsi bersifat asosiatif.
4. Ada fungsi nol yang unik sehingga ketika ditambahkan ke fungsi apa pun, fungsi yang sama diperoleh.
5. Untuk fungsi yang diberikan Y (x), ada fungsi unik –Y (x) sehingga Y (x) + (–Y (x)) = 0.
6. Penggandaan fungsi dengan bilangan kompleks apa pun memberikan fungsi dan linier.
7. Properti distribusi diamati, yang artinya
z [Y (x) + j (x)] = zY (x) + zj (x),
[z + w] Y (x) = zY (x) + wY (x),
di mana z dan b adalah bilangan kompleks.
Semua ini menyiratkan bahwa kita dapat mengidentifikasi fungsi Y (x) dengan vektor ket | Y〉 dalam ruang vektor abstrak. Tidak mengherankan bahwa kita juga dapat mendefinisikan bra-vektor. Vektor bra 〈Y | yang sesuai dengan chum sal | Y〉 diidentifikasi dengan fungsi konjugat kompleks Y * (x).
Untuk menggunakan ide ini secara efektif, kita perlu menggeneralisasi beberapa objek dari seperangkat alat matematika kita. Dalam kuliah sebelumnya, label yang mengidentifikasi fungsi gelombang adalah anggota dari beberapa set diskrit terbatas, misalnya, nilai eigen dari beberapa yang dapat diamati. Tetapi sekarang variabel independennya kontinu. Antara lain, ini berarti bahwa kita tidak dapat meringkasnya menggunakan jumlah biasa. Saya pikir Anda tahu apa yang harus dilakukan. Berikut adalah pengganti yang berorientasi fungsi untuk tiga konsep vektor kami, dua di antaranya sudah Anda kenal.
• Jumlah digantikan oleh integral.
• Probabilitas digantikan oleh kepadatan probabilitas.
• Simbol delta Kronecker digantikan oleh fungsi Dirac delta.
Mari kita lihat lebih dekat alat-alat ini.
Jumlah digantikan oleh integral . Jika kita benar-benar ingin mempertahankan kekakuan, kita akan mulai dengan mengganti sumbu x dengan set titik diskrit yang dipisahkan oleh interval sangat kecil ε, dan kemudian beralih ke batas ε → 0. Dibutuhkan beberapa halaman untuk membenarkan setiap langkah. Tetapi kita dapat menghindari kerumitan ini dengan beberapa definisi intuitif, seperti mengganti jumlah dengan integral. Secara skematis, pendekatan ini dapat ditulis sebagai berikut:
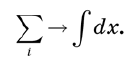
Misalnya, jika Anda perlu menghitung area di bawah kurva, sumbu x dibagi menjadi segmen-segmen kecil, maka area-area dari sejumlah besar persegi panjang ditambahkan, seperti dalam analisis matematika dasar. Ketika kami membiarkan segmen berkontraksi ke ukuran nol, jumlah tersebut menjadi integral.
Pertimbangkan brace 〈Y | dan ket | Y〉 dan tentukan produk dalam mereka. Cara yang jelas untuk melakukan ini adalah mengganti penjumlahan dalam persamaan (1.2) dengan integrasi. Kami mendefinisikan produk dalam sebagai berikut:
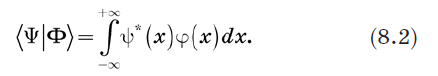Probabilitas digantikan oleh densitas probabilitas . Selanjutnya, kami mengidentifikasi P (x) = Y * (x) Y (x) dengan kepadatan probabilitas untuk variabel x. Mengapa dengan kepadatan probabilitas, dan bukan hanya dengan probabilitas? Jika x adalah variabel kontinu, maka probabilitas bahwa ia akan mengambil nilai yang diberikan biasanya nol. Oleh karena itu, lebih tepat mengajukan pertanyaan seperti ini: berapakah probabilitas x terletak di antara dua nilai x = a dan x = b? Kepadatan probabilitas ditentukan sehingga probabilitas ini diberikan oleh integral
Karena probabilitas total harus 1, kita dapat mendefinisikan normalisasi vektor sebagai
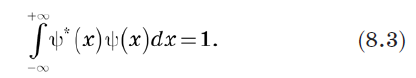Simbol delta Kronecker digantikan oleh fungsi Dirac delta . Sejauh ini, semuanya sudah sangat akrab. Fungsi Dirac Delta adalah sesuatu yang baru. Fungsi delta adalah analog dari simbol del Kronecker dij, yang menurut definisi adalah 0 jika i ≠ j, dan 1 jika i = j. Tapi itu bisa didefinisikan dengan cara lain. Pertimbangkan Fi vektor dalam ruang dimensi terbatas. Sangat mudah untuk melihat bahwa simbol Kronecker delta memenuhi syarat
Ini disebabkan oleh fakta bahwa hanya istilah dengan j = i yang bukan nol dalam jumlah ini. Selama penjumlahan, simbol Kronecker menyaring semua komponen F kecuali Fi. Generalisasi yang jelas akan menentukan fungsi baru yang memiliki properti penyaringan yang sama ketika digunakan di bawah integral. Dengan kata lain, kita memerlukan entitas baru d (x - x '), yang memiliki properti yang untuk fungsi apa pun F (x)
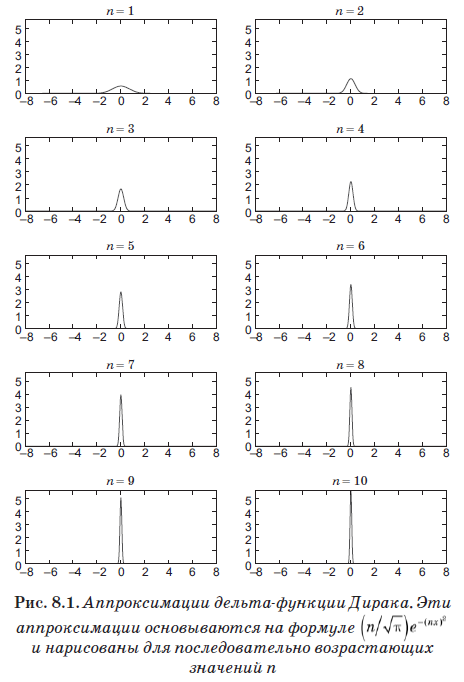
Persamaan (8.4) mendefinisikan entitas baru yang disebut fungsi Dirac delta, yang ternyata menjadi alat paling penting dalam mekanika kuantum. Namun terlepas dari namanya, ini sebenarnya bukan fungsi dalam arti biasa. Itu sama dengan nol di mana x ≠ x ', tetapi ketika x = x' ia pergi hingga tak terbatas. Faktanya, ini tidak terbatas cukup sehingga area di bawah d (x) sama dengan 1. Secara kasar, fungsi ini bukan nol pada interval kecil yang tak terhingga ε, tetapi pada interval ini ia memiliki nilai 1 / ε. Dengan demikian, area di bawahnya sama dengan 1, dan, yang lebih penting, itu memenuhi persamaan (8.4). Fungsi
mendekati fungsi delta dengan cukup baik untuk nilai n yang sangat besar. Dalam gbr. 8.1 menunjukkan optimasi ini dengan meningkatkan nilai n. Terlepas dari kenyataan bahwa kami menetapkan n = 10, yaitu nilai yang sangat kecil, perhatikan bahwa grafik telah menjadi puncak yang sangat sempit dan tajam.
»Informasi lebih lanjut tentang buku ini dapat ditemukan di
situs web penerbit»
Isi»
KutipanUntuk pembaca blog ini, diskon 20% untuk kupon -
Sasskind