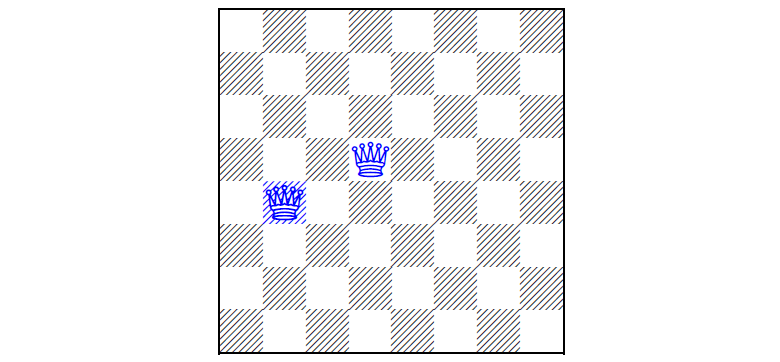
 Versi pertama dari teka-teki pada tahun 1850, ketika dua ratu sudah terpasang di papan, dan pemain harus mengatur ratu yang tersisa (untuk dua solusi masalah, lihat di bawah potongan)Tugas N queens
Versi pertama dari teka-teki pada tahun 1850, ketika dua ratu sudah terpasang di papan, dan pemain harus mengatur ratu yang tersisa (untuk dua solusi masalah, lihat di bawah potongan)Tugas N queens adalah menempatkan N queens pada papan N × N sehingga tidak ada ratu yang berada di bawah pertempuran yang lain, dengan beberapa ratu yang sudah terpasang di papan. Artinya, pada akhirnya, tidak ada dua ratu yang harus berada pada garis atau diagonal yang sama. Masalahnya pertama kali dirumuskan pada tahun 1848, dan pada tahun 1850 mereka datang dengan varian puzzle, ketika sejumlah ratu diletakkan di papan terlebih dahulu, dan pemain harus mengatur sisanya, jika mungkin.
Para peneliti di St Andrews University (Skotlandia) menerbitkan sebuah
artikel ilmiah yang membuktikan bahwa masalah N-Queens tidak hanya # P-complete, tetapi juga NP-complete. Selain itu, Clay Institute of Mathematics (USA) siap membayar satu juta dolar kepada siapa saja yang dapat mengoptimalkan solusi untuk masalah ini sebagai masalah bukti P = NP.
Seperti yang Anda ketahui, dalam teori kompleksitas, #P adalah kelas masalah yang solusinya adalah jumlah yang berhasil, yaitu menyelesaikan dalam kondisi penerimaan, jalur komputasi untuk beberapa mesin Turing non-deterministik yang bekerja pada waktu polinomial. Masalah komputasi kelas # P (masalah penghitungan) terkait dengan masalah keputusan terkait kelas NP.
Para ilmuwan mencatat bahwa tugas ini mungkin yang paling sederhana di antara tugas-tugas NP-lengkap untuk menjelaskan esensi dari masalah ini kepada siapa saja yang mengetahui aturan permainan catur. Tugas ini memiliki kisah yang sangat menarik. Pada suatu waktu, dia menarik perhatian Gauss, yang bahkan membuat kesalahan kecil dalam keputusannya (di dewan 8 × 8, dia melaporkan 76 keputusan, tetapi kemudian dia mengakui empat dari mereka salah, sehingga hanya 72 yang tersisa, dan kemudian Gauss menetapkan semua 92 keputusan) untuk papan 8 × 8).
Generalisasi masalah untuk papan N × N telah menarik perhatian banyak matematikawan. Selama setengah abad terakhir, beberapa lusin karya ilmiah yang ditujukan untuk masalah ini telah diterbitkan. Setidaknya enam dari mereka dikutip lebih dari 400 kali di Google Cendekia: ini adalah Golomb & Baumert, 1965; Bitner & Reingold, 1975; Mackworth & Freuder, 1985; Minton, Johnston, Philips, & Laird, 1992; Selman, Levesque & Mitchell, 1992; Crawford, Ginsberg, Luks, & Roy, 1996.
Kompleksitas masalah N-Queens sering salah menilai. Bahkan dalam banyak karya yang dikutip, sering disebut masalah NP-hard (NP-hard), tetapi akan menjadi seperti itu hanya jika P = NP. Faktanya, versi komputasi masalah, yaitu menentukan jumlah solusi untuk N queens, adalah
urutan A000170 dari Encyclopedia Online Integer Sequences. Urutan ini sekarang dikenal maksimum untuk n = 27, di mana jumlah solusi melebihi 2,34 × 1017. Tidak ada satu solusi yang lebih efektif untuk masalah ini yang diketahui selain pencarian lengkap sederhana. Jadi, untuk n = 27 pada 2016, pencarian paralel skala besar pada FPGA digunakan.
Pada saat yang sama, jika komputer mulai menyebutkan kemungkinan posisi ratu pada papan sel 1000 × 1000, maka itu akan memuat tugas ini selamanya. Menurut para ilmuwan, jika seseorang menemukan cara yang sangat cepat dan efektif untuk menyelesaikannya, mereka akan dapat memperoleh manfaat darinya lebih dari satu juta dolar dari Clay Institute of Mathematics. "Jika Anda menulis sebuah program yang dapat menyelesaikan masalah dengan sangat cepat, Anda dapat mengadaptasinya untuk menyelesaikan banyak tugas penting yang kita hadapi setiap hari," kata profesor ilmu komputer Ian Gent, salah satu penulis karya ilmiah. "Di antara mereka ada masalah sepele, seperti menemukan grup terbesar teman-teman Anda di Facebook yang tidak saling kenal, atau tugas yang sangat penting, misalnya kode peretasan yang menjamin keamanan semua transaksi online kami."
Tapi ini semua hanya rekayasa teoritis. Dalam praktiknya, belum ada yang mendekati solusi masalah N queens secara cepat dan efektif. Sebagai bukti bahwa ada cara yang lebih efektif untuk menyelesaikan masalah daripada penghitungan sederhana semua opsi, mereka akan memberikan satu juta dolar.
Sebuah artikel ilmiah
diterbitkan pada Agustus 2017 di jurnal
Journal of Artificial Intelligence Research (doi: 10.1613 / jair.5512,
pdf ).
PS Dua solusi untuk masalah dengan KDPV:
