Buku “Teoritis minimum. Semua yang perlu Anda ketahui tentang fisika modern ”

"Teoritis minimum" adalah buku untuk mereka yang melewatkan pelajaran fisika di sekolah dan institut, tetapi sudah menyesalinya. Ingin memahami dasar-dasar ilmu pengetahuan alam dan mempelajari cara berpikir dan bernalar seperti yang dilakukan fisikawan modern? Dalam bentuk asli dan non-standar, ilmuwan Amerika terkenal Leonard Sasskind dan George Grabowski menawarkan kursus pengantar dalam matematika dan fisika untuk pikiran ingin tahu.

Tidak seperti buku-buku non-fiksi lainnya yang mencoba menjelaskan hukum fisika dengan cara yang mudah diakses, dengan cerdik menghindari persamaan dan rumus, penulis mengajarkan pembaca dasar-dasar klasik ilmu-ilmu alam. Buku ini menawarkan metodologi pengajarannya sendiri yang asli, dilengkapi dengan video ceramah yang diterbitkan di teoricalminimum.com .

Kuliah 9. Cairan fase dan teorema Gibbs - Liouville

Lenny suka memandangi sungai, terutama menyaksikan bintik-bintik kecil mengambang di permukaan. Dia mencoba membayangkan bagaimana mereka akan bergerak di antara batu atau jatuh ke pusaran air. Tetapi aliran sungai secara keseluruhan - gerakan gabungan dari volume besar air, dengan aliran yang memisahkan, menyatu dan menyalip satu sama lain - berada di luar pemahamannya.

Fluida fase

Berkonsentrasi pada kondisi awal tertentu dan mengikuti lintasan terpisah dalam ruang fase sangat alami untuk mekanik klasik. Tetapi ada juga pandangan yang lebih luas yang mencakup seluruh keluarga lintasan. Alih-alih menempatkan ujung pensil pada titik tertentu dalam ruang fase dan menelusuri satu-satunya jalan dari sana, kita akan mencoba melakukan sesuatu yang lebih ambisius. Bayangkan bahwa kita memiliki jumlah pensil yang tak terbatas, dan menggunakannya agar kita mengisi ruang fase secara seragam dengan titik-titik (dengan homogenitas, maksudku kepadatan titik di ruang q, p sama di mana-mana). Pertimbangkan titik-titik ini sebagai partikel yang membentuk cairan imajiner yang mengisi ruang fase.

Sekarang, biarkan setiap titik bergerak sesuai dengan persamaan gerak Hamilton:


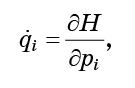
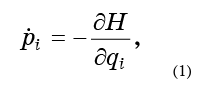
sehingga cairan kita mengalir tanpa henti melalui ruang fase.

Osilator harmonik adalah contoh awal yang bagus. Dalam kuliah 8, kami melihat bahwa setiap titik bergerak dalam orbit melingkar dengan kecepatan sudut konstan. (Biarkan saya mengingatkan Anda bahwa kita berbicara tentang fase, bukan mengkoordinasikan ruang. Dalam koordinat, osilator bergerak bolak-balik dalam satu dimensi.) Seluruh fluida secara keseluruhan membuat gerakan yang solid, berputar secara seragam di sekitar asal ruang fase.

Sekarang kembali ke kasus umum. Jika jumlah koordinat adalah N, maka ruang fase dan cairan di dalamnya adalah 2N-dimensi. Cairan mengalir, tetapi dengan cara yang sangat spesifik. Alurnya memiliki sifat khusus. Salah satunya adalah bahwa jika suatu titik dimulai dengan energi tertentu - yaitu, untuk nilai H (q, p) - maka ia menyimpan nilai energi ini. Permukaan energi konstan (misalnya, dengan energi sama dengan E) ditentukan oleh persamaan H (q, p) = E. (2)

Untuk setiap nilai E, kami memiliki satu persamaan dengan variabel ruang fase 2N yang mendefinisikan permukaan dimensi 2N - 1. Dengan kata lain, setiap nilai E memiliki permukaannya sendiri; ketika Anda memeriksa semua nilai E, permukaan ini mengisi seluruh ruang fase. Kita dapat mempertimbangkan ruang fase dengan permukaan yang diberikan oleh persamaan (2) sebagai peta kontur (Gambar 1), di mana garis horizontal mewakili bukan ketinggian, tetapi nilai energi. Jika titik cair berada pada permukaan tertentu, ia akan tetap berada di sana selamanya. Ini adalah hukum kekekalan energi.

Ruang fase osilator harmonik adalah dua dimensi, dan permukaan energi adalah lingkaran:

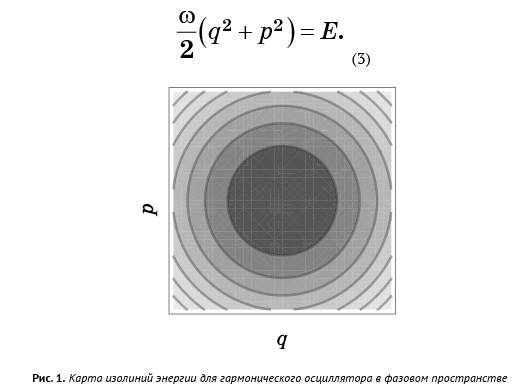
Dalam kasus umum, permukaan energi dari sistem mekanis terlalu rumit untuk divisualisasikan, tetapi prinsipnya tetap sama: permukaan energi mengisi ruang fase sebagai lapisan, dan aliran bergerak sehingga titik-titik tetap pada permukaan tempat mereka semula .

Pengingat singkat

Saya ingin berhenti di sini dan mengingat apa yang dikatakan dalam kuliah pertama, di mana koin, tulang, dan ide-ide sederhana tentang hukum gerak dibahas. Kami menggambarkan undang-undang ini dengan serangkaian panah yang menghubungkan titik-titik yang mewakili kondisi sistem. Kami juga menjelaskan bahwa hukum dapat diterima dan tidak dapat diterima, sementara yang dapat diterima bersifat reversibel. Intinya adalah bahwa setiap titik harus memiliki tepat satu panah masuk dan tepat satu panah keluar. Jika setidaknya pada satu titik jumlah panah yang masuk melebihi jumlah yang keluar (ini disebut konvergensi), maka hukum seperti itu tidak dapat diubah. Hal yang sama berlaku untuk kasus ketika ada lebih banyak panah keluar daripada yang masuk (ini disebut divergence). Divergensi dan konvergensi panah melanggar reversibilitas dan dilarang. Sejauh ini, kami belum kembali ke jalur pemikiran ini. Sekarang waktunya telah tiba.

Aliran dan perbedaan

Perhatikan beberapa contoh sederhana aliran fluida di ruang biasa. Untuk sesaat, kita lupa tentang ruang fase dan hanya menganggap fluida biasa bergerak di ruang tiga dimensi biasa dengan sumbu dilambangkan sebagai x, y, z. Alurnya dapat digambarkan oleh bidang kecepatan . Bidang kecepatan

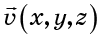
ditentukan dengan mengatur vektor kecepatan pada setiap titik dalam ruang (Gbr. 2).

Anda juga dapat menggambarkan bidang kecepatan dengan komponen kecepatan:

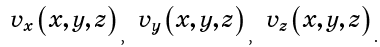
Juga, kecepatan pada suatu titik mungkin tergantung pada waktu, tetapi mari kita asumsikan bahwa tidak ada ketergantungan seperti itu. Dalam hal ini, aliran disebut stasioner .

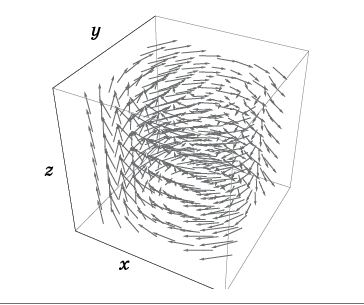
Fig. 2. Bidang kecepatan

mengambil jumlah yang sama. Ini juga berarti bahwa kepadatan cairan - jumlah molekul per satuan volume - adalah sama di mana-mana dan konstan sepanjang waktu. Ngomong-ngomong, istilah "ketidakmampatan" juga berarti tidak dapat diperpanjang. Dengan kata lain, cairan tidak bisa bertambah volumenya. Pertimbangkan sel kubik kecil yang didefinisikan oleh kondisi:

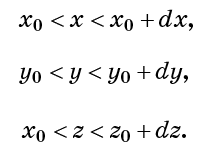
Ketidakterkompresian menyiratkan bahwa jumlah titik cairan di setiap sel tersebut konstan. Ini juga berarti bahwa total aliran cairan yang memasuki sel (per satuan waktu) harus nol. (Berapa banyak titik aliran yang masuk, jumlah yang sama keluar.) Pertimbangkan jumlah molekul yang lewat per satuan waktu melalui permukaan sel x = x0. Ini akan sebanding dengan kecepatan aliran pada permukaan ini vx (x0).

Jika kecepatan vx sama pada x0 dan pada x0 + dx, maka aliran ke dalam sel melalui x = x0 akan sama dengan aliran darinya melalui x = x0 + dx. Tetapi jika vx berubah di seluruh sel, maka kedua aliran ini akan menjadi tidak seimbang. Aliran total yang masuk ke sel melalui dua wajah ini akan proporsional

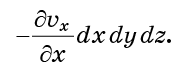
Pertimbangan yang persis sama berlaku untuk wajah y0 dan y0 + dy, serta z0 dan z0 + dz. Jika semuanya ditambahkan, maka total aliran molekul ke dalam sel (inflow minus outflow)

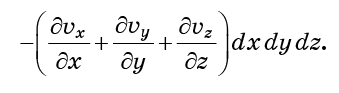
Kombinasi turunan dalam tanda kurung disebut divergensi bidang vektor
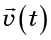
dan ditunjuk

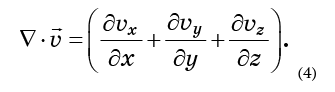
Divergensi mencerminkan tingkat dispersi molekul, atau peningkatan volume yang ditempati oleh mereka. Jika fluida tidak dapat dimampatkan, volume ini tidak boleh berubah, yang berarti bahwa divergensi harus nol.

Salah satu cara untuk memahami ketidakmampatan adalah dengan membayangkan setiap molekul atau titik menempati volume yang tidak dapat diubah. Mereka tidak dapat dikompresi menjadi volume yang lebih kecil, mereka tidak menghilang dan tidak muncul entah dari mana. Dengan sedikit pemikiran, Anda dapat melihat betapa tidak kompresif dan reversibelnya serupa. Dalam contoh yang kami analisis dalam kuliah 1, panah juga menentukan jenis aliran. Dan pada dasarnya aliran ini tidak dapat dimampatkan, setidaknya jika itu dapat dibalik. Pertanyaan alami yang mengikuti dari ini adalah: apakah aliran dalam ruang fase reversibel? Jawabannya adalah ya, jika sistem memenuhi persamaan Hamilton. Dan teorema yang mengungkapkan ketidakkompresan ini disebut teorema Liouville.

Teorema Liouville

Mari kita kembali ke aliran fluida dalam ruang fase dan mempertimbangkan komponen-komponen kecepatan fluida di setiap titik dalam ruang fase. Tidak perlu dikatakan bahwa fluida fase tidak tiga dimensi dalam koordinat x, y, z. Ini adalah fluida 2N-dimensi dalam koordinat pi, qi.

Dengan demikian, ada komponen 2N dari bidang kecepatan - satu untuk setiap koordinat q dan setiap koordinat p. Biarkan mereka

Konsep divergensi yang dinyatakan oleh persamaan (4) mudah digeneralisasikan ke sejumlah dimensi. Dalam tiga dimensi, ini adalah jumlah turunan dari komponen kecepatan dalam arah yang sesuai. Dengan cara yang sama, ditentukan untuk sejumlah dimensi. Dalam kasus ruang fase, perbedaan aliran adalah jumlah anggota 2N:

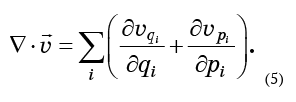
Jika fluida tidak dapat dimampatkan, maka ungkapan ini harus nol. Untuk menghitungnya, Anda perlu mengetahui komponen medan kecepatan - mereka, tentu saja, tidak lain adalah kecepatan partikel-partikel fluida fase.

Vektor aliran pada titik tertentu diidentifikasi dengan kecepatan partikel imajiner pada titik itu. Dengan kata lain

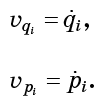
Apalagi
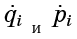
- ini hanya jumlah yang masuk ke persamaan Hamilton (1):


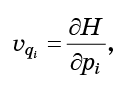
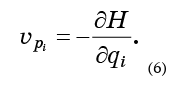
Yang perlu dilakukan adalah mengganti persamaan (6) menjadi rumus (5) dan dapatkan

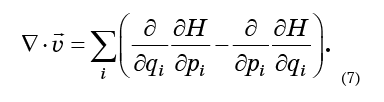
Ingat bahwa turunan kedua dari formulir


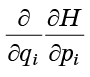
tidak tergantung pada urutan diferensiasi, kita akan memahami bahwa ketentuan persamaan (7) saling menghancurkan secara berpasangan:


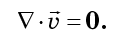
Jadi, fluida fase tidak dapat dimampatkan. Dalam mekanika klasik, ketidakmampatan fluida fase disebut teorema Liouville, meskipun hampir tidak ada hubungannya dengan ahli matematika Prancis Joseph Liouville. Ini pertama kali diterbitkan pada tahun 1903 oleh fisikawan besar Amerika Josiah Willard Gibbs, dan juga dikenal sebagai teorema Gibbs - Liouville.

Kami menentukan ketidakmampatan suatu fluida dengan mensyaratkan bahwa jumlah total cairan yang memasuki sel kecil apa pun adalah nol. Ada definisi lain yang sangat setara. Bayangkan volume cairan di beberapa titik waktu. Volume ini dapat memiliki bentuk apa saja: bulat, kubik, seperti jatuhkan - apa pun. Sekarang kita akan mengikuti pergerakan semua poin dari volume ini. Setelah beberapa waktu, setetes cairan akan berada di tempat yang berbeda dan memiliki bentuk yang berbeda. Tetapi jika fluida tidak bisa dimampatkan, volume tetesan akan tetap sama seperti aslinya. Jadi kita dapat merumuskan kembali teorema Liouville: volume yang ditempati oleh setetes cairan fase dipertahankan dalam waktu .

Pertimbangkan contoh osilator harmonik di mana fluida berputar di sekitar titik referensi. Jelas, drop mempertahankan volume, karena semua gerakannya dikurangi menjadi rotasi solid-state. Bentuk drop tetap tidak berubah, tetapi ini adalah kasus untuk osilator harmonik. Pertimbangkan contoh lain. Misalkan Hamiltonian memiliki bentuk H = pq.

Mungkin ini bagi Anda tidak seperti orang Hamilton, meskipun itu sepenuhnya benar. Kami menurunkan persamaan gerak:

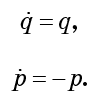
Menurut persamaan ini, q meningkat secara eksponensial dengan waktu, dan p secara eksponensial berkurang dengan kecepatan yang sama. Dengan kata lain, aliran tersebut menekan fluida terhadap sumbu p, sambil memperluasnya di sepanjang sumbu q ke tingkat yang sama. Setiap penurunan meluas di sepanjang q dan kontrak di sepanjang hal. Jelas, drop mengalami deformasi yang luar biasa, tetapi volume fase tidak berubah.

Teorema Liouville adalah analog terdekat dari jenis irreversibilitas yang kita bahas dalam Kuliah 1. Dalam mekanika kuantum, teorema Liouville digantikan oleh versi kuantum yang disebut unitarity. Unitaritas bahkan lebih mirip dengan apa yang kita bahas dalam kuliah 1, tetapi ini adalah topik dari The Theoretical Minimum edisi berikutnya.

»Informasi lebih lanjut tentang buku ini dapat ditemukan di situs web penerbit
» Seruan
» Kutipan

Untuk pembaca blog ini, diskon 20% pada kupon - Minimum teoretis