Setelah menuangkan pasir di piring elastis berosilasi, orang dapat melihat pembentukan tokoh-tokoh Hladni . Mereka sering berfungsi sebagai contoh dari "keindahan alam" dari fenomena fisik, meskipun di belakang mereka adalah fisika yang agak sederhana dari eksitasi resonansi gelombang berdiri. Dan hanya sedikit orang yang memperhatikan fitur penasaran dari tokoh-tokoh ini: garis-garis pada mereka menghindari persimpangan, seolah-olah beberapa kekuatan mengusir mereka. Mari kita coba untuk memahami jenis fisika apa yang tersembunyi di balik tolakan ini dan bagaimana hubungannya dengan teori kuantum kekacauan.

Gelombang yang berdiri

Seperti yang kita tahu, benda-benda elastis dapat membuat getaran yang agak rumit, di mana mereka berkontraksi, meregang, menekuk, dan memuntir. Namun demikian, getaran dari setiap benda elastis dapat direpresentasikan sebagai kombinasi dari getaran normal yang lebih sederhana yang saling menindih satu sama lain. Ini adalah bagaimana beberapa getaran normal dari tubuh elastis sederhana - string yang direntangkan satu dimensi - terlihat seperti.

Setiap osilasi normal diwakili oleh gelombang berdiri , yang, tidak seperti gelombang bepergian, diam dan memiliki pola sendiri distribusi amplitudo dari osilasi di ruang angkasa. Dalam gambar ini, antinode dapat dibedakan - titik di mana amplitudo osilasi mencapai maksimum, dan simpul - titik tetap di mana amplitudo osilasi adalah nol. Selain itu, setiap gelombang tersebut berosilasi dengan frekuensinya sendiri . Dalam kasus string, seperti yang Anda lihat, frekuensi osilasi gelombang berdiri meningkat dengan meningkatnya jumlah node dan antinode.


Mari kita lihat sistem dua dimensi, contohnya adalah membran elastis tipis yang direntangkan di atas kerangka yang kaku. Getaran normal dari membran bundar terlihat lebih rumit daripada dalam kasus string, dan alih-alih titik individu-node ada garis - garis nodal di mana membran itu diam.


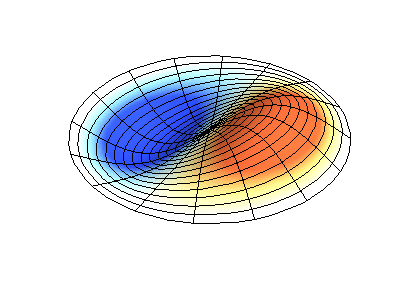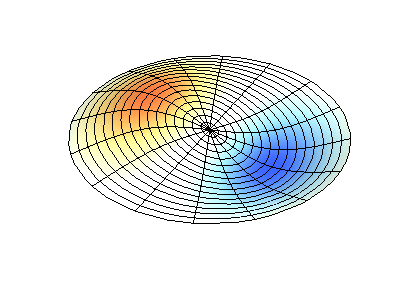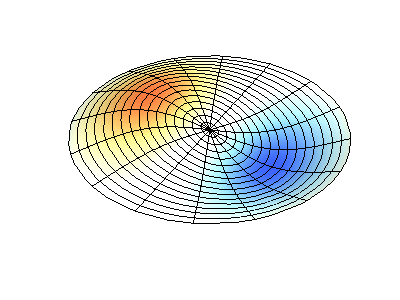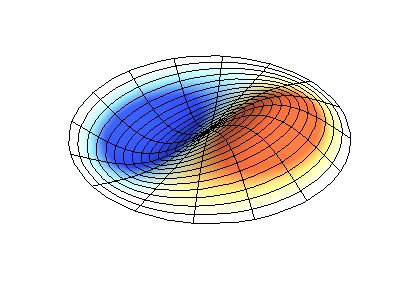
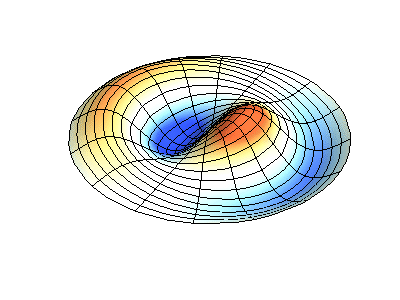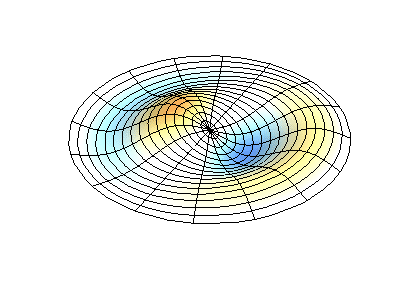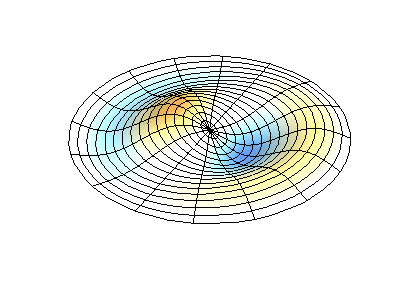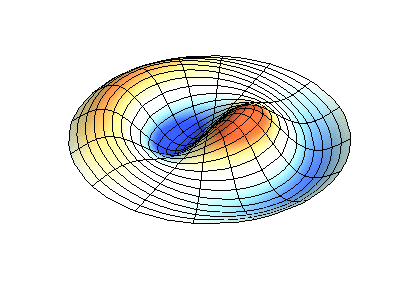
Getaran normal dari membran bundar dengan tepi tetap. Sumber


Warna hijau menunjukkan garis nodal.

Pada membran bundar, garis nodal, yang merupakan lingkaran dan segmen sepanjang jari-jari, dapat berpotongan di sudut kanan. Jika ujung-ujung membran memiliki bentuk yang sewenang-wenang, menemukan frekuensi getaran normal dan pola dari simpul dan antinodanya berubah menjadi masalah yang hanya dapat diselesaikan dengan menggunakan komputer.

Profil amplitudo osilasi gelombang berdiri pada membran dalam bentuk kotak dengan lubang , butiran salju Koch dan permukaan anak kucing .

Persamaan yang menggambarkan osilasi dari pelat elastis tipis berbeda dari persamaan osilasi membran, karena pelat memiliki kekakuan sendiri, sedangkan membran lunak dan kenyal hanya karena ketegangan oleh kekuatan eksternal. Namun, ada juga set getaran normal, gambar yang secara substansial tergantung pada bentuk batas.

Tokoh Hladni

Seperti disebutkan di atas, dalam kasus umum, getaran tubuh adalah kombinasi dari seluruh rangkaian getaran normal yang bergairah di dalamnya. Fenomena resonansi memungkinkan Anda untuk secara aktif mengeluarkan salah satu dari getaran normal yang kita butuhkan - untuk ini kita perlu mengayunkan tubuh menggunakan kekuatan eksternal dengan frekuensi yang sama dengan frekuensi alami dari osilasi normal.

Dua video di bawah ini menunjukkan skema khas untuk memperoleh angka Hladni: pelat elastis dipasang di tengah ke generator getaran mekanis, frekuensi yang secara bertahap meningkat. Getaran lempeng normal dengan pola titik dan antinodesnya bersemangat ketika frekuensi osilator secara resonansi cocok dengan frekuensi alami dari getaran ini (frekuensi alami ditunjukkan dalam video di sudut kiri bawah).

Berikut adalah versi dari video yang sama di mana frekuensi getaran normal dapat diperkirakan oleh telinga.

Dan ini sedikit lebih cantik.

Kita melihat pola knot dan antinode karena fakta bahwa aliran udara di dekat lempeng berosilasi menghembuskan butiran pasir ke garis nodal gelombang berdiri ^(*) . Dengan demikian, angka-angka Hladni menunjukkan kepada kita pola garis nodal dari getaran normal pada pelat elastis.

Beberapa tokoh Hladni ada di dek atas gitar. Sumber

Contoh lain dari gelombang normal adalah gelombang berdiri di permukaan air. Mereka dideskripsikan oleh persamaan yang berbeda dari persamaan getaran lempeng dan membran, tetapi mengikuti hukum kualitatif yang sama, dan dengan bantuan mereka dimungkinkan untuk mendapatkan analog dari angka-angka Hladni.

Mikropartikel pada permukaan air dalam bejana berbagai bentuk. Garis hitam menunjukkan skala 2 milimeter. Sumber

Kekacauan klasik

Jadi, kami melihat bahwa dalam kasus membran bulat, garis nodal secara teoritis! - sangat berpotongan, pada saat yang sama, pada angka Hladni di piring persegi atau lebih kompleks, garis nodal menghindari persimpangan. Untuk memahami alasan dari pola-pola ini, kita harus bertamasya singkat ke teori kekacauan.

Kekacauan klasik adalah sifat sistem mekanis, yang terdiri dari ketergantungan lintasan gerakan mereka yang sangat kuat terhadap perubahan kondisi awal. Hubungan ini juga dikenal sebagai " efek kupu-kupu ". Contoh nyata dari perilaku kacau dapat ditemukan dalam upaya untuk memprediksi cuaca: sistem persamaan yang menggambarkan pergerakan atmosfer dan lautan tidak memungkinkan prakiraan yang cukup akurat dibuat pada waktu yang lama karena kesalahan yang meningkat secara eksponensial karena ketidakakuratan kecil dalam data awal. ^(**) .

Fenomena kekacauan secara terbuka dan dipopulerkan oleh ahli meteorologi dan matematika Edward Lorenz , yang menemukan bahwa dua perhitungan ramalan cuaca dimulai dengan kondisi awal yang sangat dekat pada awalnya hampir tidak dapat dibedakan, tetapi pada titik tertentu mereka mulai menyimpang secara radikal.

Dua perhitungan oleh Edward Lorenz, mulai dari nilai awal dekat 0,506 dan 0,506127. Sumber

Sistem yang paling sederhana, pada contoh yang nyaman untuk dipelajari kekacauan, adalah biliar - bagian dari permukaan datar di mana bola dapat menggelinding tanpa gesekan, benar-benar elastis memantul dari dinding yang kaku. Dalam biliar yang kacau, lintasan bola, yang memiliki sedikit perbedaan di awal, kemudian menyimpang secara signifikan. Contoh biliar yang kacau adalah biliar Sinai yang ditunjukkan di bawah ini, yang merupakan kolam persegi panjang dengan rintangan melingkar di tengah. Seperti yang akan kita lihat, justru karena kendala inilah biliar menjadi kacau.

Dua lintasan bola yang berbeda secara eksponensial di biliar Sinai. Sumber

Sistem yang terintegrasi dan kacau

Sistem mekanis yang tidak kacau disebut integrable , dan dengan contoh biliar, Anda dapat dengan jelas melihat perbedaan antara sistem integrable dan kacau.

Biliar persegi panjang dan bulat dapat dipadukan karena bentuknya yang simetris ^(***) . Pergerakan bola dalam biliar tersebut hanyalah kombinasi dari dua gerakan periodik independen. Dalam biliar persegi panjang, ini adalah gerakan dengan memantul dari dinding secara horizontal dan vertikal, dan secara keseluruhan ini adalah gerakan di sepanjang jari-jari dan gerakan sudut dalam lingkaran di sekitar pusat. Gerakan seperti itu mudah dihitung dan tidak menunjukkan perilaku kacau.

Lintasan bola dalam biliar yang dapat digabungkan.

Biliar dengan bentuk yang lebih kompleks, tidak memiliki simetri setinggi lingkaran atau persegi panjang, kacau balau ^(****) . Salah satunya yang kita lihat di atas adalah biliar Sinai, di mana simetri persegi panjang dihancurkan oleh inklusi melingkar di tengah. Yang juga sering dipertimbangkan adalah biliar "stadion" dan biliar dalam bentuk siput Pascal. Bola bergerak dalam biliar yang kacau di sepanjang jalan yang sangat rumit dan tidak terurai menjadi gerakan periodik yang lebih sederhana.

Lintasan bola di "stadion" biliar yang kacau dan "siput Pascal."

Di sini Anda sudah dapat menebak bahwa keberadaan persimpangan antara garis-garis pada gambar Hladni ditentukan oleh apakah lempengan tersebut memiliki bentuk biliar yang dapat terintegrasi atau kacau. Ini terlihat jelas di foto-foto di bawah ini.

Piring bundar Hladni, menunjukkan sifat-sifat biliar terintegrasi. Sumber

Menunjukkan sifat biliar kacau piring Hladni dalam bentuk biliar "stadion", kasus biola dan alun-alun, simetri yang rusak oleh perlengkapan bundar di tengah (analogi biliar Sinai). Sumber

Kekacauan kuantum

Bagaimana memahami mengapa persimpangan antara garis-garis nodal disebabkan oleh keterpaduan biliar? Untuk melakukan ini, kita perlu beralih ke teori kuantum kekacauan , menggabungkan teori kekacauan dengan mekanisme osilasi dan gelombang. Jika dalam mekanika klasik bola dalam biliar digambarkan sebagai titik material yang bergerak di sepanjang lintasan tertentu, maka dalam mekanika kuantum gerakannya digambarkan sebagai perambatan gelombang yang mematuhi persamaan Schrödinger dan dipantulkan dari dinding biliar.

Tahapan propagasi gelombang dalam biliar kuantum. Awalnya, gelombang terkonsentrasi dalam pulsa bulat dan bergerak dari kiri ke kanan, kemudian menyebar dan berulang kali terpantul dari dinding. Sumber

Sama dalam bentuk animasi, tetapi dengan kondisi awal yang sedikit berbeda.

Seperti dalam kasus getaran membran dan pelat, persamaan Schrödinger yang menggambarkan biliar kuantum memungkinkan seseorang untuk menemukan getaran normal dalam bentuk gelombang berdiri, yang memiliki pola karakteristik garis nodal dan antinode, masing-masing untuk setiap getaran dan tergantung pada bentuk batas.

Contoh profil amplitudo osilasi dalam gelombang berdiri di biliar kuantum kacau " siput Pascal " dan " stadion ".

Pola gelombang berdiri dalam biliar kuantum integrable dan chaotic berbeda secara kualitatif: biliar integrable menunjukkan pola gelombang berdiri simetris, sedangkan dalam biliar kacau pola gelombang berdiri sangat membingungkan dan tidak menunjukkan pola yang terlihat (pada akhir artikel akan ditunjukkan bahwa beberapa yang menarik pola di sana masih ada).

Osilasi amplitudo dalam gelombang berdiri biliar bundar yang terintegrasi (baris atas) dan biliar kacau dalam bentuk siput Pascal (baris bawah). Sumber

Gambar-gambar aneh dari getaran normal di biliar yang kacau kadang-kadang berfungsi sebagai subjek penelitian terpisah. Sumber

Perbedaan kualitatif juga terlihat dalam pola garis nodal: dalam kasus biliar kuantum yang dapat diintegrasikan, kita melihat keluarga yang dipesan dari garis yang berpotongan satu sama lain , dan dalam biliar yang kacau, garis ini, sebagai suatu peraturan, tidak berpotongan .

Atas: garis nodal (garis hitam antara area biru dan merah) dari gelombang berdiri biliar bulat - bulat dan persegi panjang. Bawah: garis nodal dari salah satu gelombang berdiri di biliar yang kacau - seperempat dari biliar stadion .

Berpotongan atau tidak berpotongan?

Mengapa garis nodal di biliar yang kacau tidak berpotongan? Pada tahun 1976, ahli matematika Karen Uhlenbeck membuktikan teorema yang dengannya garis-garis nodal gelombang biliar kuantum, secara umum, tidak boleh berpotongan.

Dalam bentuk yang disederhanakan, ini dapat ditunjukkan sebagai berikut: misalkan dua garis nodal berpotongan pada suatu titik ( x ₀ , y ₀ ). Agar ini terjadi, fungsi f ( x, y ), yang menentukan ketergantungan amplitudo gelombang berdiri pada koordinat, harus secara bersamaan memenuhi tiga kondisi:

1) Itu harus sama dengan nol pada titik ( x ₀ , y ₀ ), karena titik ini adalah nodal.
2) Jika Anda bergerak dari titik ( x ₀ , y ₀ ) ke arah garis nodal pertama, maka f ( x, y ) harus tetap sama dengan nol.
3) Jika Anda bergerak dari titik ( x ₀ , y ₀ ) ke arah garis nodal kedua, maka f ( x, y ) juga harus tetap sama dengan nol.


Secara total, kami memiliki tiga kondisi (atau tiga persamaan) yang dikenakan pada fungsi dua variabel f ( x, y ). Seperti yang kita ketahui, satu persamaan tidak cukup untuk sepenuhnya menemukan dua yang tidak diketahui x dan y , dua persamaan sudah cukup untuk ini, dan tiga persamaan terlalu banyak. Sistem tiga persamaan untuk dua yang tidak diketahui, secara umum, tidak akan memiliki solusi, kecuali kita cukup beruntung. Oleh karena itu, titik persimpangan garis nodal hanya bisa ada sebagai pengecualian .

Dalam biliar yang dapat diintegrasikan, pengecualian seperti itu baru saja muncul. Seperti yang kita lihat di atas, sifat khusus mereka - dapat diprediksi gerakan, tidak adanya kekacauan, pola gelombang berdiri yang teratur - adalah hasil dari simetri tinggi mereka. Simetri yang sama memastikan pemenuhan simultan dari tiga kondisi yang diperlukan untuk persimpangan garis nodal.

Mari kita lihat lebih dekat contoh-contoh tokoh Hladni yang khas dari biliar yang bisa terintegrasi dan kacau. Gambar di bawah ini menunjukkan tiga kasus karakteristik . Di sebelah kiri, piring memiliki bentuk lingkaran, sehingga biliar kuantum yang sesuai dapat diintegrasikan, dan garis nodal saling berpotongan. Di tengah, pelat persegi panjang, yang juga sesuai dengan sistem yang dapat diintegrasikan, namun, pemasangan putaran di tengah sedikit melanggar simetri persegi panjang, sehingga garis nodal tidak berpotongan di mana-mana. Contoh dari sistem yang benar-benar kacau ditampilkan di sebelah kanan: piring dalam bentuk seperempat dari biliar Sinai (di sudut kanan atas ada guntingan bundar), garis nodal di mana tidak lagi berpotongan.



Dengan demikian, semakin kuat bentuk pelat - dengan mempertimbangkan pengikatannya - berbeda dari bentuk biliar terintegrasi (seperti lingkaran atau persegi panjang), semakin sedikit persimpangan garis-garis nodal di atasnya .

Tidak mudah untuk mendapatkan figur Hladni yang cantik dengan garis berpotongan di atas piring bundar. Ketika getaran yang menggairahkan dengan pengikat pusat, simetri melingkar dari seluruh sistem melarang pembentukan garis nodal radial, jadi kita hanya akan melihat serangkaian lingkaran yang membosankan (kesulitan ini dapat diatasi dengan getaran yang menarik bukan dari pusat, tetapi dari tepi pelat menggunakan busur dari biola). Jika pelat dipasang di tengah, angka-angka Hladni akan menjadi lebih menarik, tetapi karena pelanggaran simetri sirkuler, sistem akan berhenti menjadi tidak terintegrasi.

Pelat bundar, dudukan tengah.

Piring bundar, mount bergeser dari tengah.

Dan di sini ada beberapa pilihan dengan pelat bulat dan non-lingkaran.

Akhirnya, seorang pembaca yang penuh perhatian mungkin memperhatikan: tetapi saya melihat bahwa kadang-kadang garis-garis nodal berpotongan bahkan di atas piring "kacau". Bagaimana mungkin jika persimpangan mereka dilarang oleh teorema Uhlenbeck?

Pertama, garis-garis nodal dapat menghindari persimpangan, tetapi sebelum itu mereka menjadi sangat dekat sehingga karena lebar jalur pasir yang terbatas, tampaknya bagi kita bahwa ada persimpangan. Kedua, antara sistem yang terintegrasi dan kacau, pada kenyataannya, tidak ada batas yang tajam.

Garis nodal - mereka memisahkan area hitam dan putih - dalam biliar kuantum yang dapat diintegrasikan dan kacau (kiri dan kanan), dan dalam kasus pseudo-integrable antara (di tengah). Dalam kasus menengah, ada beberapa persimpangan dari garis nodal, sedangkan dalam kasus kacau tidak ada sama sekali. Sumber

Dalam teori klasik chaos, teori Kolmogorov-Arnold-Moser yang terkenal dikhususkan untuk masalah ini. Dia mengatakan bahwa jika simetri dari sistem yang dapat diintegrasikan sedikit dilanggar, itu tidak akan segera menunjukkan perilaku kacau, tetapi, sebagian besar, akan mempertahankan prediktabilitas gerakannya. Pada tingkat teori chaum dan tokoh-tokoh Hladni kuantum, ini dimanifestasikan dalam kenyataan bahwa di beberapa tempat persimpangan garis-garis nodal dipertahankan. Ini terjadi pada titik-titik biliar yang simetris, atau jauh dari sumber gangguan, yang melanggar simetri sistem yang dapat diintegrasikan.

Apa lagi

Apa lagi yang menarik dalam teori kekacauan kuantum? Untuk pembaca yang tertarik, saya akan menyebutkan tiga pertanyaan tambahan yang tidak lagi berhubungan langsung dengan tokoh-tokoh Hladni.

1) Fenomena penting yang dipelajari oleh teori ini adalah universalitas sistem kacau. Sebagian besar sistem di mana getaran normal dapat terjadi adalah kacau, dan semuanya - terlepas dari sifat fisiknya! - patuhi hukum yang sama. Fenomena universalitas, di mana sistem yang sama sekali berbeda dijelaskan oleh formula yang sama, itu sendiri sangat indah dan berfungsi sebagai pengingat kesatuan matematika dari dunia fisik.

Statistik jarak antara frekuensi yang berdekatan dari getaran normal dalam sistem kacau dari sifat fisik yang berbeda, di mana-mana dijelaskan oleh rumus Wigner-Dyson universal yang sama. Sumber

2) Pola getaran normal biliar kacau memiliki fitur menarik yang disebut "bekas luka kuantum" . Kita telah melihat bahwa jalur bola di biliar yang kacau biasanya terlihat sangat membingungkan. Tapi ada pengecualian - ini adalah orbit periodik , lintasan yang cukup sederhana dan pendek di sepanjang bola membuat gerakan periodik. Bekas luka kuantum disebut penebalan tajam gelombang berdiri di sepanjang orbit periodik.

Bekas luka kuantum di "stadion" biliar, membentang di sepanjang orbit periodik yang ditunjukkan oleh garis merah dan hijau. Sumber

3) Sejauh ini kita telah berbicara tentang sistem dua dimensi. Jika kita mempertimbangkan perambatan gelombang dalam ruang tiga dimensi, maka garis nodal juga dapat muncul di sini di mana amplitudo osilasi adalah nol. Ini sangat penting ketika mempelajari kondensasi dan superfluiditas Bose, di mana ribuan atom bergerak sebagai " gelombang materi " tunggal. Analisis struktur garis nodal gelombang materi dalam ruang tiga dimensi diperlukan, misalnya, untuk memahami bagaimana turbulensi kuantum muncul dan berkembang dalam sistem superfluida.

Terjebak struktur tiga dimensi dari garis nodal berdiri "gelombang materi" di kondensat Bose. Sumber .

^(*) Jika ukuran partikel yang dituangkan ke piring cukup kecil, maka partikel-partikel itu akan tertiup bukan ke node, tetapi ke antinode dari gelombang berdiri, seperti yang ditunjukkan dalam karya eksperimental ini .

^(**) «» «» , : – , , . .

^(***) – . , , , .

^(****) Untuk lebih tepatnya, kepemilikan biliar ke integrable atau kacau tergantung pada jumlah integral gerak independen- jumlah yang bertahan dari waktu ke waktu. Biliar terintegrasi memiliki dua integral gerak, dalam sistem dua dimensi ini cukup untuk solusi analitik yang tepat dari persamaan gerak. Biliar yang kacau hanya memiliki satu integral gerakan - energi kinetik bola.