Koneksi rahasia matematika dan fisika murni terungkap

Seorang ahli matematika yang luar biasa telah mengungkapkan rincian tentang bagaimana keberhasilannya dalam studi masalah matematika ribuan tahun terkait dengan konsep yang diambil dari fisika.

Mignon Kim

Matematika penuh dengan sistem bilangan aneh yang belum pernah didengar kebanyakan orang. Beberapa di antaranya bahkan akan sulit dibayangkan. Tetapi bilangan rasional sudah biasa bagi semua orang. Ini adalah angka untuk menghitung objek dan fraksi - semua angka yang kita ketahui dari sekolah dasar. Namun dalam matematika, terkadang paling sulit untuk memahami hal-hal yang paling sederhana. Mereka sederhana, seperti dinding yang halus, tanpa retakan dan tonjolan, atau sifat jelas lainnya yang bisa Anda ambil.

Minion Kim , seorang ahli matematika di Universitas Oxford, sangat tertarik dengan pertanyaan bilangan rasional mana yang cocok untuk menyelesaikan persamaan dari jenis tertentu. Masalah ini telah merangsang spesialis dalam teori bilangan selama ribuan tahun. Dan mereka nyaris tidak membuat kemajuan ke arah solusi. Ketika sebuah pertanyaan telah dipelajari begitu lama dan tanpa jawaban, dapat disimpulkan bahwa satu-satunya cara untuk maju di dalamnya adalah mengedepankan ide baru yang radikal. Inilah yang dilakukan Kim.

“Tidak banyak teknologi yang ada, meskipun kami telah mengerjakan ini selama 3000 tahun terakhir. Jadi ketika seseorang menemukan cara yang benar-benar baru dalam melakukan ini, itu sangat menarik - dan Mignon melakukan hal itu, "kata Jordan Ellenberg, ahli matematika di University of Wisconsin di Madison.

Selama dekade terakhir, Kim telah menggambarkan cara yang sama sekali baru untuk menemukan pola-pola dalam dunia angka-angka rasional yang tampaknya tidak teratur. Dia menggambarkan metode ini dalam artikel dan konferensi, dan meneruskannya kepada siswa yang sekarang melanjutkan pekerjaan ini sendiri. Tapi dia selalu menyelamatkan sesuatu. Visinya, yang menghidupkan ide-idenya, tidak didasarkan pada dunia angka murni, tetapi pada konsep-konsep yang dipinjam dari fisika. Bagi Kim, keputusan rasional agak mengingatkan pada lintasan cahaya.


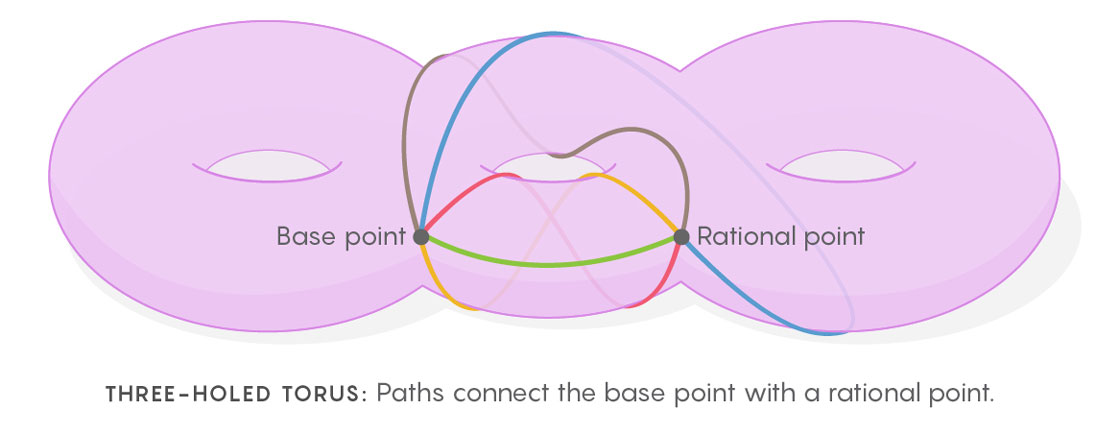
Objek matematika, torus tiga lubang, menghiasi papan Kim di Universitas Oxford.

Jika hubungan ini tampak fantastis, maka itu, bahkan untuk ahli matematika. Karena itu, Kim tidak mengungkapkan detailnya untuk waktu yang lama. "Saya menyembunyikannya karena selama bertahun-tahun saya bingung oleh koneksi dengan fisika," katanya. "Spesialis dalam teori bilangan adalah orang yang sangat praktis, dan pengaruh fisika terkadang membuat mereka skeptis terhadap matematika."

Tetapi sekarang Kim mengatakan dia siap untuk membagikan visinya. "Aku pikir perubahan hanyalah gejala penuaan!" - menulis Kim, yang berusia 53 tahun, dalam salah satu surat pertama yang kami tukar untuk menulis cerita ini.

Dia baru-baru ini mengadakan konferensi yang mempertemukan para pakar dalam teori bilangan dan teori string. Dia juga membuat sketsa draft artikel yang mulai menggambarkan inspirasinya untuk komunitas matematika, tidak terbiasa berpikir tentang angka menggunakan analogi langsung seperti itu dengan dunia fisik.

Hanya satu kendala yang tersisa - bagian terakhir dari analogi fisika dalam matematika, yang belum berhasil diselesaikan Kim. Dia berharap bahwa dengan mengundang orang lain untuk membagikan visinya, terutama fisikawan, dia akan menerima bantuan yang diperlukan untuk menyelesaikan pekerjaan.

Teka-teki kuno

Solusi rasional persamaan secara aktif menarik pikiran manusia. Mereka membawa kepuasan, mirip dengan apa yang Anda dapatkan dari potongan puzzle yang sesuai dengan tempatnya. Oleh karena itu, mereka adalah pahlawan hipotesis matematika paling terkenal.

Bilangan rasional mencakup bilangan bulat dan angka apa pun yang dapat dinyatakan sebagai rasio dua bilangan bulat, misalnya, 1, -4 atau 99/100. Matematikawan sangat tertarik pada bilangan rasional yang menyelesaikan persamaan Diophantine - persamaan polinomial dengan koefisien bilangan bulat, misalnya, x ² + y ² = 1. Mereka dinamai sesuai dengan ahli matematika Diophantus , yang mempelajarinya di Alexandria pada abad ke-3 M.

Solusi rasional sulit ditemukan dalam kasus umum, karena tidak mematuhi keteraturan geometris. Ambil persamaan x ² + y ² = 1. Solusi dalam bilangan real membentuk lingkaran. Hapus semua titik pada lingkaran yang tidak dapat dinyatakan sebagai pecahan, dan hanya keputusan rasional yang akan tersisa yang tidak membentuk objek yang begitu rapi. Solusi rasional terlihat tersebar secara acak di sekitar keliling.



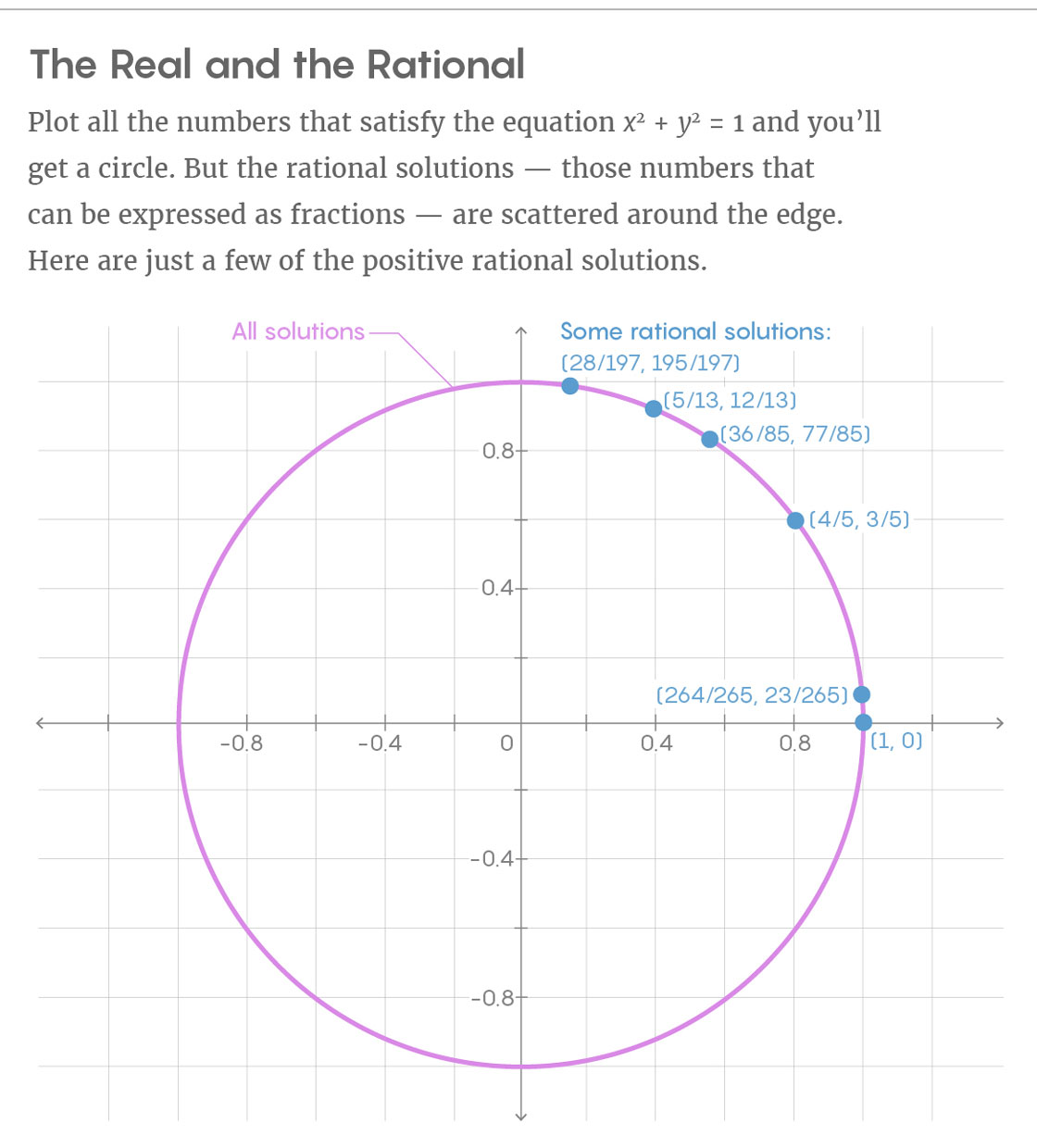
“Kondisi yang harus dipatuhi titik agar memiliki koordinat rasional sama sekali tidak geometris. Tidak mungkin untuk menulis persamaan yang harus dipenuhi oleh poin-poin rasional, "kata Kim.

Seringkali cukup sederhana untuk menemukan satu solusi rasional, atau bahkan beberapa. Tetapi matematikawan yang tidak suka meremehkan lebih tertarik untuk menemukan semua solusi rasional. Dan ini jauh lebih rumit. Sangat sulit bahwa, bukti bahkan pernyataan minor tentang jumlah keputusan rasional cukup untuk lulus untuk seorang termasyhur matematika. Pada tahun 1986, Gerd Falting memenangkan Fields Prize , penghargaan matematika tertinggi, terutama untuk membuktikan hipotesis Mordell , yang mengatakan bahwa kelas-kelas tertentu dari persamaan Diophantine hanya memiliki sejumlah terbatas solusi rasional.

Bukti Falting adalah titik balik dalam teori bilangan. Dan juga oleh apa yang oleh para ahli matematika disebut "bukti tidak efektif", karena tidak memberikan jumlah tepat dari solusi rasional dan tidak menemukan mereka. Sejak itu, matematikawan telah mencari cara untuk melakukan langkah selanjutnya. Poin rasional terlihat acak pada grafik persamaan reguler. Matematikawan berharap bahwa dengan mengubah konteks di mana mereka merenungkan masalah, poin-poin ini dapat dibuat terlihat seperti kombinasi yang bermakna yang dapat dijelaskan dengan cara yang tepat. Masalahnya adalah bahwa bidang matematika yang terkenal tidak menyediakan konteks seperti itu.


Kim di kantornya di Oxford

"Untuk mendapatkan hasil yang efektif dari titik rasional, jelas ada kebutuhan untuk ide baru," kata Ellenberg.

Sekarang ada dua asumsi utama tentang sifat gagasan semacam itu. Salah satunya berasal dari ahli matematika Jepang Shinichi Motizuki , yang menerbitkan pada tahun 2012 sebuah karya matematika yang kompleks dan inovatif beberapa ratus halaman di halaman fakultasnya di Universitas Kyoto. Lima tahun kemudian, pekerjaan ini sebagian besar tetap tidak dapat dipahami. Gagasan baru lainnya datang dari Kim, yang mencoba membayangkan bilangan rasional dalam konteks numerik yang diperluas di mana pola tersembunyi mereka mulai muncul.

Solusi Simetris

Matematikawan sering mengatakan bahwa semakin obyek simetris, semakin mudah untuk mempelajarinya. Oleh karena itu, mereka ingin menempatkan studi persamaan diophantine dalam kondisi yang mengandung lebih banyak simetri daripada yang di mana masalah ini muncul secara alami. Jika ini berhasil, mereka akan dapat menggunakan simetri yang baru ditemukan untuk melacak titik-titik rasional yang mereka butuhkan.

Untuk memahami bagaimana simetri membantu ahli matematika menavigasi masalah, bayangkan sebuah lingkaran. Mungkin tujuan Anda adalah mengidentifikasi semua poin di lingkaran. Simetri banyak membantu, karena ia menciptakan peta yang memungkinkan Anda untuk berpindah dari titik yang Anda tahu ke titik yang masih harus ditemukan.

Bayangkan Anda telah menemukan semua titik rasional di bagian bawah lingkaran. Karena lingkaran memiliki simetri cermin, titik-titik dapat dipantulkan ke atas (mengubah tanda sama sekali koordinat y) dan tiba-tiba mendapatkan semua poin dari atas. Lingkaran pada umumnya memiliki simetri yang kaya sehingga untuk mencari semua titik di atasnya, Anda perlu mengetahui posisi hanya satu titik, dan kemudian menggabungkannya dengan pengetahuan tentang simetri lingkaran: Anda hanya perlu menerapkan simetri rotasi tak terbatas dari lingkaran ke titik awal.

Tetapi jika objek geometri tempat Anda bekerja jauh kurang benar, seperti, misalnya, jalur pengibaran acak, Anda harus banyak bekerja untuk menentukan setiap titik secara terpisah - Anda tidak akan memiliki hubungan simetris yang memungkinkan Anda untuk menandai titik yang tidak diketahui saat bantu terkenal.

Set numerik juga dapat memiliki simetri, dan semakin banyak simetri dalam satu set, semakin mudah dipahami - Anda dapat menerapkan hubungan simetris untuk mendeteksi nilai yang tidak diketahui. Angka dengan tipe simetri tertentu membentuk "grup", dan matematikawan menggunakan properti grup untuk memahami angka yang terkandung di dalamnya.

Banyak solusi rasional persamaan tidak harus memiliki simetri dan tidak membentuk kelompok, itulah sebabnya matematikawan dihadapkan dengan tugas yang tidak realistis dalam mencoba menemukan solusi satu per satu.

Dari tahun 1940-an, matematikawan mulai mempelajari metode untuk mengatur persamaan Diophantine dalam kondisi yang lebih simetris. Matematikawan Claude Chabauty menemukan bahwa di dalam ruang geometris yang lebih besar yang ia ciptakan (menggunakan semesta bilangan yang disebut bilangan p-adic ), bilangan rasional membentuk subruang simetris mereka sendiri. Dia mengambil subruang ini dan menggabungkannya dengan plot persamaan Diophantine. Titik-titik persimpangan mereka ternyata merupakan solusi rasional dari persamaan tersebut.

Pada 1980-an, matematikawan Robert Coleman menentukan pekerjaan Chaboti. Selama beberapa dekade berikutnya, pendekatan Coleman-Chaboti adalah alat matematikawan terbaik matematika harus menemukan solusi rasional untuk persamaan Diophantine. Tapi itu hanya berfungsi jika grafik persamaan berkorelasi dengan ukuran ruang yang lebih besar dalam proporsi tertentu. Ketika rusak, menjadi sulit untuk secara akurat menemukan posisi titik persimpangan kurva persamaan dan bilangan rasional.

"Jika kurva Anda berada di lingkungan di mana ada terlalu banyak titik rasional, mereka mulai menumpuk dan sulit bagi Anda untuk membedakan mana yang ada di kurva," kata Kiran Kedlaya, seorang ahli matematika di University of California, San Diego.

Dan kemudian Kim masuk. Untuk memperluas karya Chaboti, ia ingin menemukan ruang yang lebih besar untuk mempelajari persamaan Diophantine - ruang di mana bilangan rasional lebih terfragmentasi, yang memungkinkan kita untuk mempelajari titik persimpangan dengan sejumlah besar variasi persamaan Diophantine.

Spasi ruang

Jika Anda membutuhkan ruang yang lebih besar dan beberapa petunjuk tentang bagaimana Anda dapat menggunakan simetri untuk mengarahkan diri Anda di dalamnya, fisika akan cocok untuk Anda.

Dalam kasus umum, ruang dalam pengertian matematika adalah sekumpulan titik dengan struktur geometris atau topologi. Seribu poin tersebar dengan kehendak atau tidak, tidak membentuk ruang - mereka tidak terhubung bersama oleh suatu struktur. Tapi bola, yang merupakan organisasi poin yang terhubung, sudah ruang. Seperti torus, atau bidang dua dimensi, atau ruang-waktu empat dimensi, tempat kita tinggal.

Selain itu, ada lebih banyak ruang eksotis yang dapat dibayangkan sebagai "ruang ruang". Contoh paling sederhana: katakanlah Anda memiliki segitiga - dan ini adalah ruang. Sekarang bayangkan ruang semua segitiga yang mungkin. Setiap titik di dalamnya mewakili segitiga tertentu, dan koordinat titik ini ditentukan oleh sudut segitiga yang diwakili olehnya.

Gagasan seperti itu sering berguna dalam fisika. Dalam kerangka teori relativitas umum, ruang dan waktu terus berkembang, dan fisikawan menganggap setiap konfigurasi ruang dan waktu sebagai titik dalam ruang semua konfigurasi ruang-waktu. Spasi ruang juga muncul di area yang oleh fisikawan disebut invarian gauge, bekerja dengan bidang yang ditumpangkan pada ruang fisik. Bidang-bidang ini menggambarkan bagaimana gaya-gaya seperti elektromagnetisme dan gravitasi berubah ketika bergerak di ruang angkasa. Orang dapat membayangkan bahwa pada setiap titik dalam ruang konfigurasi bidang-bidang ini sedikit berbeda - dan bahwa semua konfigurasi yang berbeda ini membentuk titik-titik dalam "ruang semua bidang" dimensi yang lebih tinggi.

Ruang bidang ini dari fisika adalah analogi yang dekat dengan proposal Kim untuk teori bilangan. Untuk memahami hal ini, bayangkan sinar cahaya. Fisikawan mewakili cahaya yang bergerak melalui ruang bidang dimensi yang lebih tinggi. Di ruang ini, cahaya akan mengikuti jalur yang menganut prinsip resistensi terendah dan meminimalkan jumlah waktu yang diperlukan untuk berpindah dari titik A ke titik B. Prinsip ini menjelaskan mengapa cahaya membungkuk saat bergerak dari satu bahan ke bahan lainnya - jalur lengkung meminimalkan waktu biaya.

Ruang yang lebih besar dari ruang yang muncul dalam fisika memiliki simetri tambahan yang tidak ada dalam ruang yang mereka wakili. Simetri ini menarik perhatian ke titik-titik tertentu, misalnya, berfokus pada jalur yang meminimalkan waktu. Simetri yang sama, dibangun dalam cara yang berbeda dan dalam konteks yang berbeda, dapat ditekankan pada titik-titik lain - misalnya, pada titik-titik yang sesuai dengan solusi persamaan yang rasional.

Menghubungkan Simetri dengan Fisika

Dalam teori bilangan, tidak ada partikel yang dapat dilacak, tetapi ia memiliki sesuatu seperti ruang-waktu, dan ia menawarkan cara untuk menggambar jalur dan menciptakan ruang dari semua jalur yang mungkin. Dari korespondensi dasar ini, Kim mengembangkan skema di mana "masalah menemukan lintasan cahaya dan menemukan solusi rasional dari persamaan Diophantine adalah dua wajah dari masalah yang sama," saat ia menjelaskan pada sebuah konferensi tentang fisika matematika di Heidelberg minggu lalu.

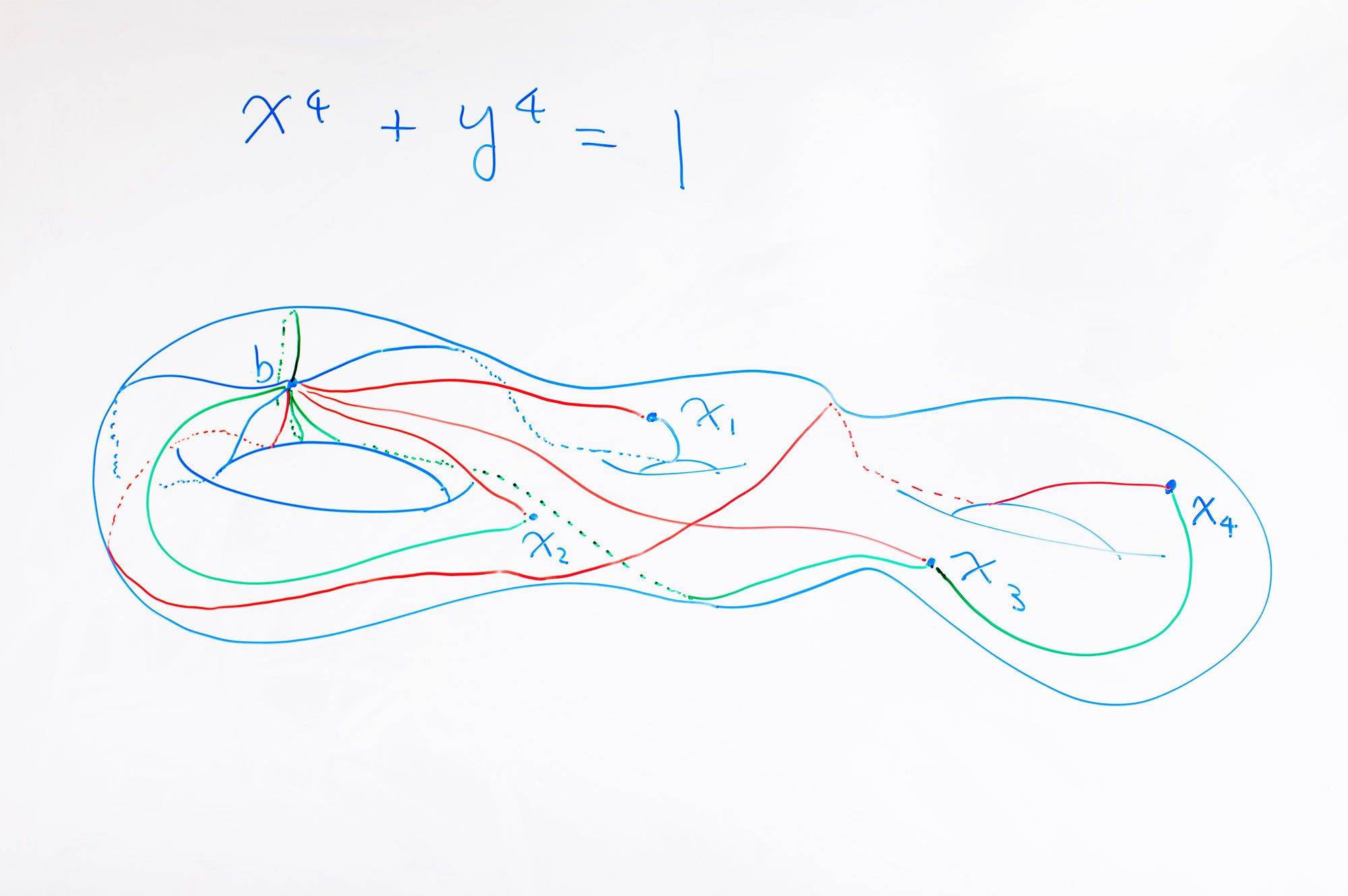
Solusi persamaan Diophantine membentuk spasi - ini adalah kurva yang didefinisikan oleh persamaan. Kurva ini bisa satu dimensi, seperti lingkaran, atau multi dimensi. Misalnya, jika Anda membuat solusi kompleks dari persamaan diophantine x ⁴ + y ⁴ = 1, Anda mendapatkan torus dengan tiga lubang. Titik-titik rasional pada torus semacam itu tidak memiliki struktur geometris - itulah sebabnya sulit untuk menemukannya - tetapi mereka dapat dibandingkan dengan titik-titik dalam ruang multidimensi ruang yang memiliki struktur seperti itu.



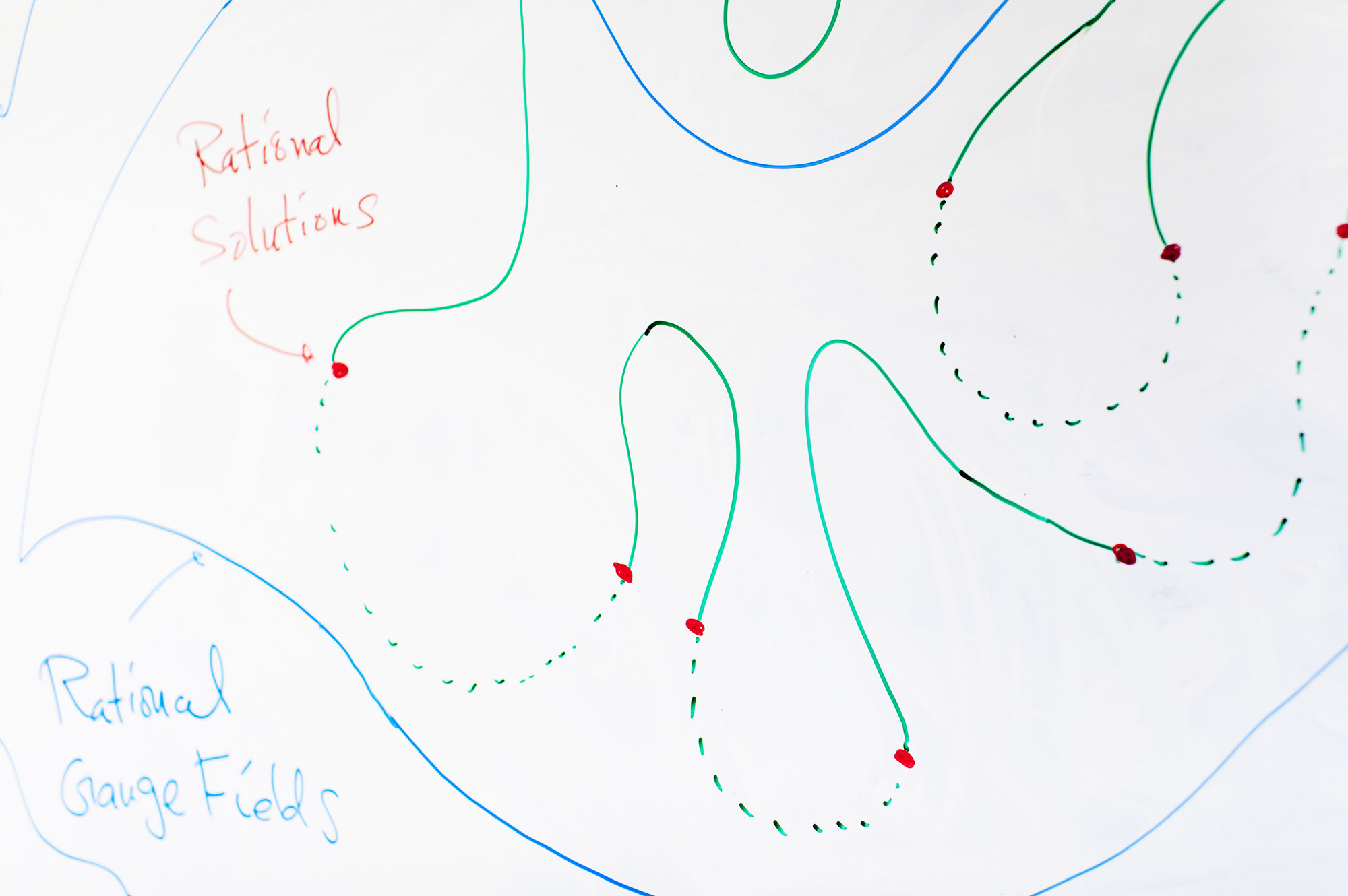
Kim menciptakan ruang ruang multidimensi ini, membayangkan cara di mana kurva tertutup dapat ditarik pada torus (atau dalam ruang yang mendefinisikan persamaan). Prosedur untuk menggambar kurva terlihat seperti ini. Pertama, Anda harus memilih titik awal, lalu menggambar satu lingkaran dari titik ini ke titik lainnya, dan kembali ke yang pertama. Sekarang ulangi proses ini, gambar jalur yang menghubungkan titik dasar dengan semua titik lain dari torus. Anda akan mendapatkan kumpulan semua kemungkinan loop mulai dan berakhir pada titik dasar. Kumpulan loop ini adalah objek matematika yang penting secara terpusat yang disebut kelompok ruang mendasar .

Setiap titik pada torus dapat digunakan sebagai titik awal. Setiap titik akan memiliki setapak jalur unik yang berasal darinya. Setiap koleksi jalur ini dapat direpresentasikan sebagai titik dalam “ruang semua set jalur” multidimensi (sebagai ruang semua segitiga yang mungkin). Ruang ruang ini secara geometris sangat mirip dengan apa yang dibangun oleh fisikawan dalam teori invarian ukur: cara set jalur berubah ketika Anda berpindah dari satu titik ke torus ke yang lain sangat mirip dengan bagaimana bidang berubah saat Anda berpindah dari satu titik ke titik lainnya. lain di ruang nyata. Ruang ruang ini memiliki simetri tambahan yang tidak ada di torus itu sendiri. Dan meskipun titik-titik rasional pada torus tidak memiliki simetri, jika kita masuk ke ruang semua set jalur, kita dapat menemukan simetri antara titik-titik yang terkait dengan bilangan rasional. Anda mendapatkan simetri yang tidak terlihat sebelumnya.

"Saya kadang-kadang mengatakan bahwa" simetri aritmatika tersembunyi "dikodekan dalam jalur ini, yang sangat mirip dengan simetri internal dari teori invarian gauge," kata Kim.

Seperti Chaboti, Kim menemukan solusi rasional dengan menjelajahi titik persimpangan di ruang yang lebih besar yang mereka buat. Dia menggunakan simetri ruang ini untuk sampai di titik persimpangan. Dia berharap untuk mengembangkan persamaan yang secara akurat mendefinisikan poin-poin ini.

Dalam konteks fisik, orang dapat membayangkan semua cara yang mungkin dilakukan oleh sinar cahaya. Ini adalah "ruang semua jalur Anda". Fisikawan tertarik pada titik-titik di ruang ini sesuai dengan jalur yang meminimalkan waktu. Kim percaya bahwa titik-titik yang berkaitan dengan belukar jalur yang berasal dari titik-titik rasional memiliki sesuatu seperti properti yang sama - yaitu, titik-titik ini meminimalkan beberapa properti yang terjadi ketika Anda mempertimbangkan bentuk geometris dari persamaan Diophantine. Dia hanya belum tahu apa properti ini mungkin.

"Apa yang saya mulai coba temukan," adalah prinsip resistensi paling tidak dalam konteks matematika, ia menulis kepada saya dalam sebuah surat. "Aku belum menemukannya, tapi aku yakin itu ada."

Masa depan yang tidak pasti

Selama beberapa bulan terakhir, saya telah menggambarkan visi Kim, yang terinspirasi oleh fisika, oleh beberapa ahli matematika, penggemar kontribusinya terhadap teori bilangan. Tetapi setelah mengetahui detail dari pekerjaannya, mereka hilang.

"Sebagai ahli teori jumlah yang representatif, jika aku ditunjukkan semua prestasi luar biasa yang dibuat oleh Minion dan ditanya apakah mereka terinspirasi oleh fisika, aku akan mengatakan: Apa yang kamu bicarakan?" - kata Ellenberg.

Sejauh ini, Kim belum menyebut fisika dalam karyanya. Sebaliknya, ia menulis tentang objek yang disebut "variasi Selmer," dan meneliti hubungan antara variasi Selmer dalam ruang semua variasi Selmer. Hal-hal seperti itu akrab bagi para pakar teori bilangan. Tetapi bagi Kim, mereka selalu merupakan sebutan lain dari objek fisik tertentu.

"Seharusnya ada cara untuk menggunakan ide-ide fisik untuk menyelesaikan masalah dalam teori bilangan, tapi kami belum cukup memikirkan bagaimana cara membuat platform seperti itu," kata Kim. "Kita berada dalam keadaan di mana pemahaman kita tentang fisika berkembang cukup baik, dan banyak spesialis dalam teori bilangan tertarik di dalamnya untuk mengambil langkah selanjutnya."

Hambatan utama pada metode Kim adalah dalam menemukan beberapa tindakan untuk meminimalkan ruang semua rangkaian loop. Di dunia fisik, pendekatan ini terlihat alami, tetapi dalam aritmatika itu tidak memiliki makna yang jelas. Bahkan para ahli matematika yang mengawasi pekerjaan Kim tidak yakin apakah dia dapat menemukannya.

"Saya pikir program Kim akan melakukan banyak hal indah bagi kita. "Saya tidak berpikir kita akan memiliki sejelas Mignon ingin memahami apakah poin rasional adalah solusi klasik untuk teori ukuran aritmatika," kata Arnav Tripathy, profesor fisika matematika di Universitas Harvard.

Saat ini, bahasa fisika hampir tidak bersinggungan dengan praktik teori bilangan. Kim yakin ini hampir pasti akan berubah. Empat puluh tahun yang lalu, fisika, geometri, dan topologi memiliki sedikit kesamaan. Kemudian pada 1980-an, beberapa matematikawan dan fisikawan, yang sekarang menjadi tokoh penting, menemukan cara yang tepat untuk menggunakan fisika untuk mempelajari sifat-sifat bentuk. Setelah pengembangan ini, area ini berubah dan tidak kembali ke metode sebelumnya.

“Saat ini secara praktis mustahil untuk tertarik pada geometri dan topologi tanpa mengetahui apa pun tentang fisika. Saya cukup yakin bahwa ini akan terjadi dengan teori bilangan juga ”dalam 15 tahun ke depan, kata Kim. "Semua koneksi sangat alami."