Kemitraan Mitra Kaluza-Klein, bagian 2

Dalam artikel sebelumnya, saya menjelaskan mengapa tampaknya pengamat naif yang tidak menyadari keberadaan dimensi tambahan bahwa partikel yang mampu bergerak dalam dimensi tambahan memiliki mitra Kaluza-Klein (KK) - versi yang lebih berat dari partikel asli. Saya menunjukkan bahwa ketika partikel awal massa m bergerak ke arah dimensi tambahan, tampaknya pengamat naif tidak bergerak dan lebih berat dari seharusnya, yaitu, seolah-olah itu adalah partikel dari jenis yang berbeda. Kelas partikel yang seharusnya baru ini, mirip dengan aslinya, tetapi lebih berat, disebut mitra QC.

Dalam kasus strip , jika partikel bermassa m bergerak melintasi strip dengan momen p, pengamat yang menganggap strip sebagai garis akan menganggap bahwa partikel tersebut adalah mitra KK dengan momentum nol dan massa M, di mana

$$

$$M ^ 2 = m ^ 2 + (p_ {lintas} / c) ^ 2> m ^ 2$$

Meskipun ini umumnya benar, maka untuk setiap massa M lebih besar dari m, harus ada mitra QC-nya sendiri. Tetapi tidak demikian - dunia kita adalah kuantum (lihat Gambar 1 dari artikel sebelumnya). Sekarang kita mencari tahu bagaimana mekanika kuantum mengubah seluruh gambar.

Fitur utama fisika kuantum yang kita butuhkan adalah bahwa untuk "partikel" kuantum yang bergerak dalam pengukuran ukuran hingga, tidak semua nilai p _{yang mungkin} diijinkan. Dalam formulasi yang lebih umum: mekanika kuantum menunjukkan bahwa "partikel" yang bergerak dalam pengukuran ukuran-terbatas hanya dapat memiliki nilai momentum tertentu dalam arah ini.

Ini adalah salah satu konsekuensi paling penting dan paling aneh dari mekanika kuantum! Pada pandangan pertama, ini benar-benar berlawanan dengan intuisi, karena apa yang dapat mencegah Anda menanyakan “partikel” dengan momentum p sedikit percepatan sehingga momentumnya sedikit berbeda dari p?

Apa itu kuantum?

Anda mungkin telah memperhatikan bahwa saya mulai mengutip kata "partikel", karena dalam konteks saat ini kita perlu membedakan istilah "partikel", yang digunakan untuk menggambarkan elektron, muon, quark, gluon dan semua partikel elementer lainnya yang diketahui, dari konsep intuitif partikel yang kita warisi dari pengalaman kita dengan debu, pasir, garam dan kerikil. Akan lebih baik untuk menyebut "partikel" seperti itu sebagai elektron, foton, Quark, dll., Kuanta, benda yang lebih licik. Kuanta ini adalah gangguan dari ladang, mereka lebih seperti gelombang daripada partikel. Cara terbaik untuk memahami kuantum adalah dengan membayangkan gelombang. Ini adalah titik linguistik penting lainnya: ketika saya mengatakan "gelombang," saya tidak bermaksud sesuatu seperti gelombang terpisah di lautan yang pecah di pantai - maksud saya adalah urutan gelombang dengan banyak lambang dan palung.

Contoh dari gelombang tersebut adalah gelombang elektromagnetik, yang juga termasuk gelombang cahaya, dapat dibedakan dengan mata kita. Bayangkan kita mengambil gelombang seperti itu - misalnya, sinar laser - dan kita meredupkan cahaya, semakin banyak. Bagaimana bisa diredam? Ternyata di dunia kuantum kita ada kilatan cahaya sekecil mungkin yang kita sebut kuantum cahaya, atau foton. Foton adalah gelombang cahaya yang tinggi dan intensitas gelombangnya adalah yang terkecil dari semua yang mungkin. Kami berutang semua konsep dan nama ini kepada Einstein, yang - terlepas dari semua ketidakpuasannya yang terkenal dengan konsekuensi konseptual mekanika kuantum - adalah salah satu pendiri teori ini.

Tidak ada yang intuitif - dari sudut pandang saya - bahwa gelombang cahaya terdiri dari kuanta, karena ini tidak dimanifestasikan dalam proses yang kami amati secara langsung. Tetapi tubuh kita, berkat proses yang tidak kita sadari, gunakan fakta ini secara konstan. Cahaya lampu tampaknya terus menerus ke otak kita, tetapi mata kita sebenarnya menyerap foton satu per satu. Terlebih lagi, saya melihat dengan mata kepala saya konfirmasi bahwa cahaya terdiri dari kuanta - saya tahu tentang ini tidak hanya dari buku.

Kita fisikawan sering menyebut kuanta cahaya ini "partikel cahaya," karena dalam banyak hal mereka berperilaku seperti partikel. Setiap foton yang bergerak dalam garis lurus dengan sendirinya, memiliki energi dan momentum tertentu; semua foton memiliki nilai massa yang sama (khususnya, nol); foton tidak dapat dibagi menjadi bagian-bagian yang lebih kecil; foton hanya dapat dipancarkan atau diserap secara keseluruhan. Sifat-sifat ini kira-kira sesuai dengan apa yang bisa diharapkan oleh intuisi kita dari partikel seperti butiran pasir, bola kaca, partikel debu, dll.

Tetapi kata "kuantum" karena banyak alasan lebih baik daripada kata "partikel", karena beberapa sifat kuanta mirip dengan sifat-sifat partikel, dan beberapa sifat gelombang. Sebuah contoh terkenal dari perilaku gelombang adalah cara kuantum untuk melewati dua pintu secara bersamaan dan berinteraksi (dalam arti yang sama bahwa gelombang berinteraksi satu sama lain dan bubungan dengan palung saling menghancurkan satu sama lain) dengan diri mereka sendiri. Dan kemudian kita akan melihat contoh lain.

Harus diingat bahwa apa yang dilakukan untuk foton juga dilakukan untuk semua "partikel" yang diketahui. Memang, masing-masing adalah jenis kuantum - gelombang setinggi mungkin di bidang yang sesuai. Elektron adalah kuantum bidang elektronik. Quark adalah kuantum bidang quark. Z-partikel adalah kuantum bidang-Z, dan sebagainya.

Kuantum - mitra QC

Inilah saatnya untuk mengetahui apa yang saya janjikan untuk menjelaskan kepada Anda: mengapa sifat gelombang kuanta menyiratkan bahwa massa partikel mitra KK mengambil nilai-nilai tertentu, dan tidak semua nilai yang mungkin, massa besar m dari “partikel” asli. Fisikawan terkenal Louis de Broglie , mengikuti jejak ide-ide pertama Einstein, dengan jelas mendefinisikan untuk pertama kalinya bahwa hubungan antara gelombang, partikel dan kuanta menyiratkan bahwa untuk kuantum ada hubungan antara:
• Dorongannya (sifat yang menyerupai sifat partikel),
• Dan panjang gelombangnya (suatu sifat yang menyerupai sifat-sifat gelombang) [dan sekali lagi, di sini “gelombang” yang kita maksud adalah urutan gelombang, dan panjang gelombang mengacu pada jarak antara puncak gelombang dalam urutan tersebut).

Dan ketergantungan ini diungkapkan secara sederhana: momentum = h / panjang gelombang

h adalah konstanta Planck yang terkenal, konstanta fundamental alam yang sama dengan kecepatan cahaya. Planck memperkenalkan konstanta ini pada tahun 1900, mencoba mengungkap satu fenomena fisik misterius. Ini adalah langkah pertama menuju sifat kuantum dunia. Setiap kali Anda mencoba menggambarkan sebuah fenomena di mana mekanika kuantum memainkan peran penting, konstanta h muncul. Dalam banyak rumus, Anda dapat melihat nilai ℏ, dan ini hanya dibagi 2 π, karena nilai ini seringkali lebih mudah untuk menyederhanakan rumus.


Fig. 1: pertimbangkan sebuah kuantum yang bergerak di sepanjang strip dan sepanjang pipa

Dalam beberapa kasus, ternyata sedikit lebih mudah untuk menjelaskan apa yang terjadi pada kuantum yang bergerak di sepanjang pipa dibandingkan dengan apa yang bergerak di sepanjang jalur yang kita gunakan dalam contoh sebelumnya. Hampir semua yang bekerja untuk pipa akan berlaku untuk strip. Karena itu, saya akan menggunakannya bersama.

Mitra QC paling ringan

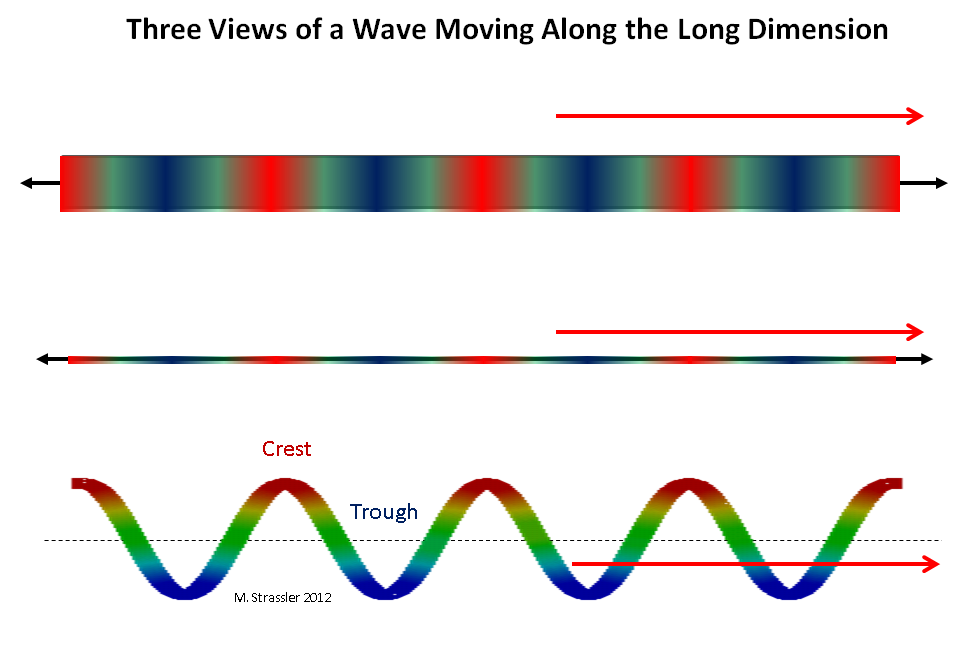Fig. 2: tiga pandangan tentang gelombang yang bergerak sepanjang dimensi panjang

Bayangkan sebuah kuantum berjalan di sepanjang strip lebar W, atau sepanjang pipa lingkaran S. Pertama, bayangkan sebuah kuantum bergerak sepanjang dimensi panjang (panjang berarti tak terbatas, atau begitu lama sehingga bisa tak terbatas, sejauh kita dapat menilai tentang hal itu). Gelombang yang berjalan di sepanjang jalur atau pipa dapat bergerak sepanjang dimensi panjang ke segala arah dan memiliki panjang gelombang apa pun (jarak antara dua bubungan yang berdekatan). Lihat gbr. 2. Kuantum semacam itu dapat memiliki momentum apa pun di sepanjang strip atau pipa, menurut de Broglie: momentum itu bisa nol, sangat kecil, kecil, besar, ke segala arah, dll. Pada prinsipnya, sebuah dorongan dapat dibuat sedikit lebih (atau sedikit kurang) dengan mendorong kuantum ke arah gerakannya (atau sebaliknya).


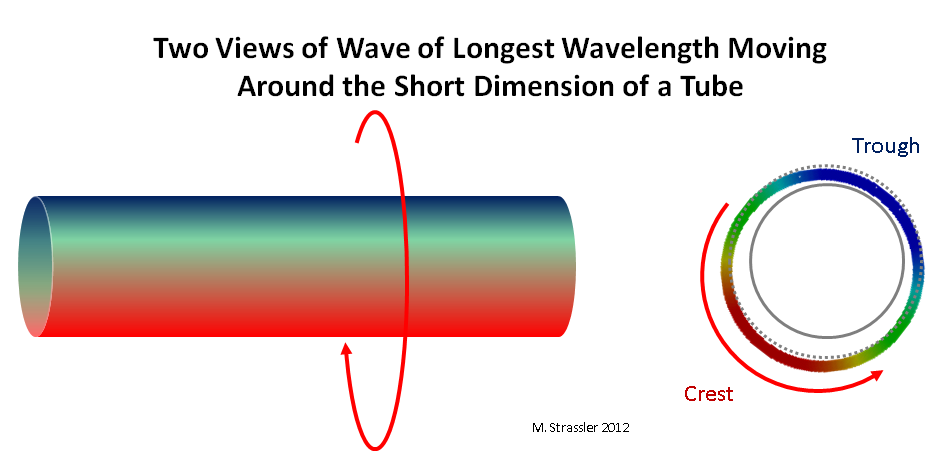Fig. 3: dua pandangan tentang gelombang yang bergerak sepanjang dimensi pendek pipa

Sekarang pertimbangkan sebuah kuantum (yaitu, "partikel") bergerak melintasi strip atau pipa. Pertama, itu jelas tidak akan dapat memiliki panjang gelombang lebih besar dari jarak transversal strip atau keliling pipa! Ini mudah dilihat pada pipa: setidaknya satu punggungan (merah) dan satu depresi (biru) yang pas di sepanjang pipa, seperti yang ditunjukkan pada gambar. 3. Jika panjang gelombang lebih besar dari S, gelombang tidak akan terhubung dengan dirinya sendiri, seperti yang ditunjukkan pada Gambar. 4. Panjang gelombang terpanjang adalah S; dan satu-satunya rongga gelombang harus terletak tepat di sisi pipa yang berseberangan dengan satu-satunya puncak.


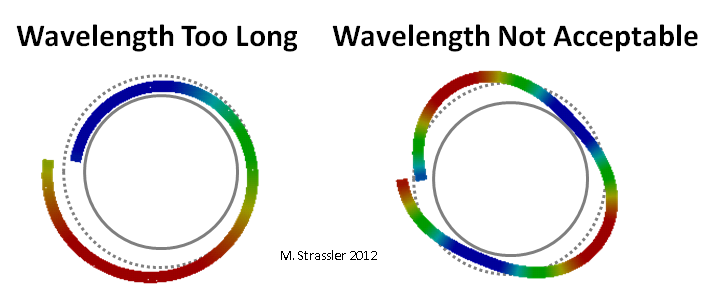Fig. 4: panjang gelombang yang tidak tepat

Puncak dan palung gelombang pada Gambar. 3 bergerak di sekitar pipa, menyerupai (Gbr. 5) partikel non-kuantum biasa (di sini saya benar-benar berarti sesuatu seperti sebutir pasir, bukan kuantum atau "partikel") bergulung di sepanjang pipa, tetapi dengan satu perbedaan penting: jika partikel intuitif biasa tidak memiliki masalah dapat bergerak sedikit lebih cepat atau lebih lambat, karena momentumnya akan naik atau turun sedikit, kuantum yang sesuai dengan gelombang tidak dapat memiliki momentum yang sedikit lebih besar atau lebih kecil, karena ini akan sesuai dengan panjang gelombang yang tidak dapat diterima (Gbr. 4).


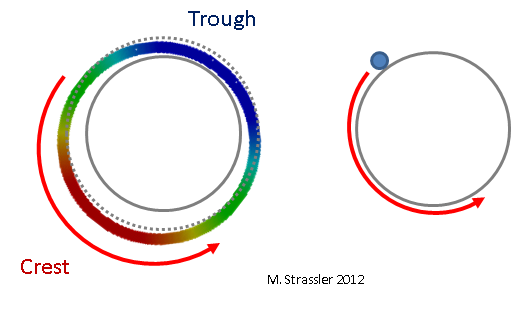Fig. 5: gelombang seperti partikel

Pada strip itu agak rumit, tetapi seperti yang ditunjukkan pada gambar. 6, sekali lagi, hanya ada satu lambang di satu dinding dan satu di yang lain, dan situasi ini berubah seiring waktu: lambang tidak bergerak, tetapi berkurang dalam ukuran dan berubah menjadi berongga, dan berongga berubah menjadi lambang. Perhatikan bahwa, berbeda dengan Gambar. 3, di mana lambang dan parit mempertahankan ukurannya tetapi bergerak di sepanjang pipa, lambang gelombang ini tidak bergerak, tetapi berkontraksi. Oleh karena itu, ini disebut "gelombang berdiri." Untuk contoh yang serupa (tetapi tidak identik), bayangkan seuntai gitar atau biola. Secara intuitif, gelombang berdiri ini bersesuaian dengan partikel non-kuantum biasa yang bergerak maju dan mundur melintasi jalur. (Kurang intuitif, tetapi lebih tepatnya, itu sesuai dengan partikel biasa yang bergerak di kedua arah pada saat yang sama. Tapi fakta kuantum yang sangat aneh dan keren ini sekarang tidak penting.) Ini ditunjukkan pada Gambar. 7.


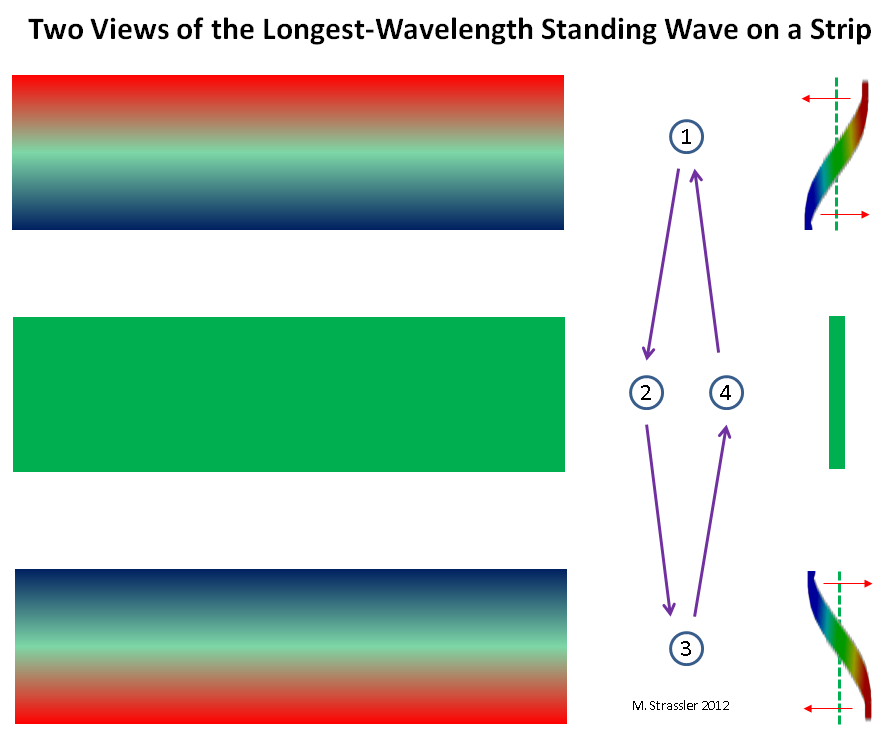Fig. 6: dua pandangan gelombang berdiri dengan panjang gelombang terpanjang

Dalam kedua kasus, ada panjang gelombang terbesar yang mungkin (S untuk pipa, 2W untuk strip). Dan ini berarti ada impuls sekecil mungkin (h / S dan h / 2 W untuk pipa dan strip). Dan akhirnya, ini berarti ada partikel KK yang termudah! Dengan massa M, di mana

$$

$$M ^ 2 = m ^ 2 + (p_ {melintasi} / c) ^ 2 = m ^ 2 + (h / c S) ^ 2 \ quad (pipa) \\ M ^ 2 = m ^ 2 + (p_ { melintasi} / c) ^ 2 = m ^ 2 + (h / 2 c W) ^ 2 \ quad (strip)$$

Perhatikan bahwa untuk partikel tanpa massa, m = 0, rumus ini direduksi menjadi:

$$

$$M = h / c S \ quad (pipa) \\ M = h / 2 c W \ quad (strip)$$

Dan formula terakhir ini kira-kira benar jika S dan W sangat kecil, seperti yang sering terjadi dalam penalaran yang masuk akal.


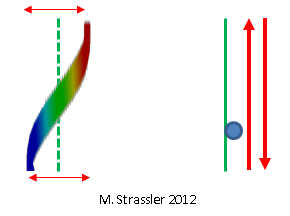Fig. 7: kuantum gelombang berdiri agak seperti partikel yang bergerak bolak-balik

Jadi kami belajar bahwa karena fakta bahwa "partikel" sebenarnya adalah kuanta, dengan sifat yang menyerupai sifat gelombang:

• Pada mitra KK paling ringan, massa M jauh lebih besar dari m,
• Karena rumus untuk M termasuk 1 / W dan 1 / S, semakin kecil dimensi tambahan, semakin sulit mitra KK paling ringan.
• Bahkan, ketika S dan W menjadi sangat kecil sehingga M jauh melebihi m (atau jika m awalnya nol sama sekali), maka M kira-kira sebanding dengan 1 / S atau 1 / W.

Bagus Ini adalah poin utama, jadi pastikan untuk memahaminya sebelum melanjutkan. Satu hal lagi yang harus dijelaskan:

• Mengapa ada banyak mitra KK dengan massa berbeda M, M ', M ”, dll. (di mana, menurut definisi, M <M '<M ”, dll.)
• Mengapa massa ini terpisah satu sama lain.
• Mengapa massa tumbuh dengan menurunnya dimensi ekstra.
• Mengapa mitra KK dari berbagai jenis partikel yang mampu bergerak dalam dimensi tambahan yang sama memiliki massa serupa, terutama untuk mitra KK yang lebih berat.
• Mengapa massa mitra QC akan memberi kami informasi langsung tentang bentuk, ukuran, dan jumlah pengukuran tambahan.

Dari jawaban di atas dapat disimpulkan dengan cukup mudah.

Di luar Mitra QC Teringan

Fig. 8: gelombang paling dekat dengan panjang gelombang terpanjang, bergerak sepanjang dimensi pendek pipa

Mengapa ada banyak mitra KK? Hanya karena gelombang kuantum pada strip atau tabung dapat memiliki banyak panjang gelombang yang berbeda. Dalam gbr. 8, 9 dan 10, seseorang dapat melihat gelombang dengan panjang 1/2 atau 1/3 maksimum, sesuai (menurut Einstein dan de Broglie) dengan kuantum impuls ganda dan tripel sehubungan dengan minimum.


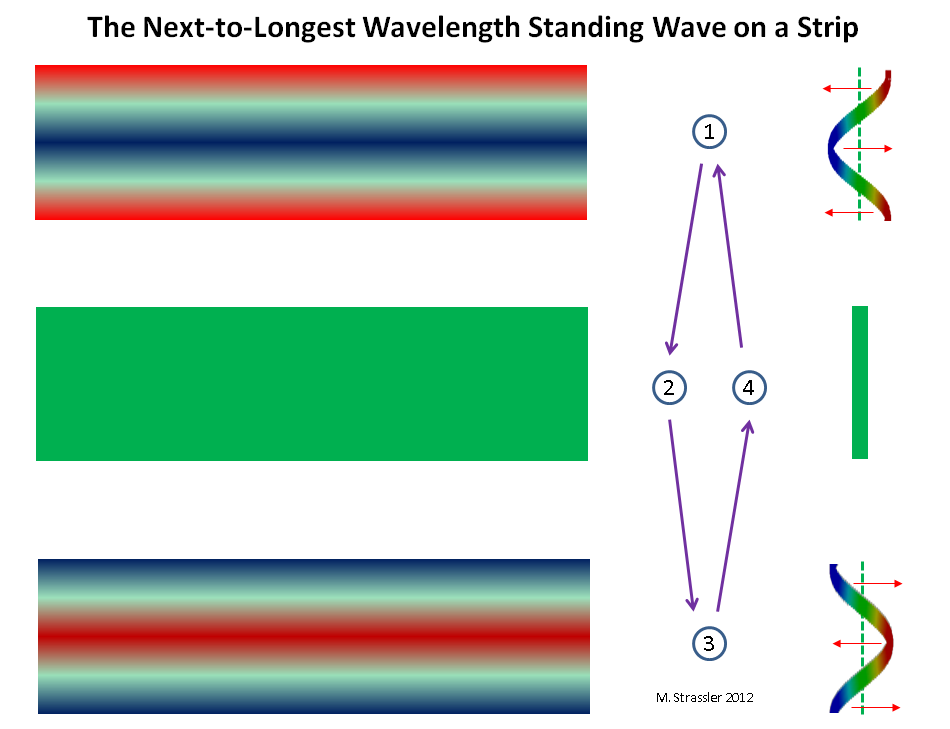Fig. 9 gelombang berdiri paling dekat dengan panjang gelombang terpanjang di strip

Ringkasnya, kita dapat mengatakan bahwa panjang gelombang apa pun dapat diterima, yang memiliki n ridges dan n palung, di mana n adalah bilangan bulat positif (1, 2, 3, 4, ..), sehingga panjang gelombang sama dengan S dibagi dengan n (atau 2W dibagi dengan n) dan gelombang dengan jelas pas di dalam lingkaran lingkaran S atau di dalam garis panjang W. Panjang gelombang lainnya tidak cocok (lihat Gambar 4). Oleh karena itu, dengan mempertimbangkan hubungan de Broglie, momentum = h / wave_length, setiap dorongan dari bentuk nh / S (atau nh / 2 W) diperbolehkan, dan untuk setiap nilai n kita akan memiliki mitra massa KK:

$$

$$M ^ 2 = m ^ 2 + (p_ {lintas} / c) ^ 2 = m ^ 2 + (nh / c S) ^ 2 \ quad (pipa) \\ M ^ 2 = m ^ 2 + (p_ { melintasi} / c) ^ 2 = m ^ 2 + (nh / 2 c W) ^ 2 \ quad (strip)$$

Ini menjawab hampir semua pertanyaan yang diajukan, setidaknya untuk kasus dengan pipa dan strip:

• Ada banyak mitra QC (satu untuk setiap n> 0),
• Massa mereka terpisah satu sama lain (karena ketika n berubah sebesar 1, M sangat banyak berubah),
• Massa mereka tumbuh dengan penurunan dimensi tambahan (karena istilah terakhir dalam rumus menjadi lebih besar ketika W dan S menjadi lebih kecil),
• Mitra KK berat dari partikel yang berbeda dengan massa berbeda m memiliki massa M yang sama, karena untuk cukup besar n istilah kedua dalam rumus adalah besar dibandingkan dengan m ² , yang memberikan massa mitra KK kira-kira sama dengan M = nh / c S untuk pipa dan nh / 2 c W untuk strip, dan hampir independen dari m.

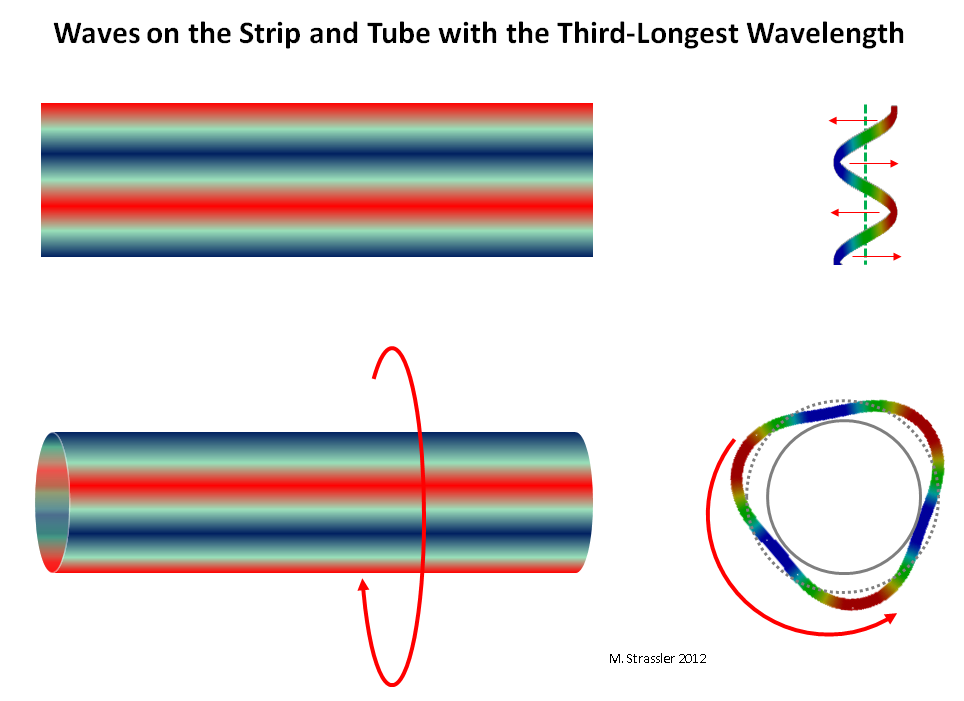Fig. 10: gelombang pada strip dan pipa dengan panjang gelombang 1/3 maksimum

Pertanyaan terakhir tetap: mengapa kuantitas, ukuran dan bentuk dimensi tambahan menentukan massa mitra KK - dan karenanya, mengapa pengukuran massa banyak mitra KK memungkinkan Anda untuk menentukan sifat-sifat pengukuran tambahan, seperti halnya mendengarkan suara alat musik memungkinkan Anda menentukan bentuknya. , ukuran dan bahan yang dibuatnya?

Ambil contoh yang sangat sederhana. Kami akan mempertimbangkan dua dimensi tambahan, lagi menggunakan saluran kapal klasik kami, termasuk (seperti yang kami lakukan di akhir artikel baru - baru ini dengan contoh-contoh pengukuran tambahan) dan fakta bahwa saluran tersebut memiliki kedalaman, sehingga kami dapat membayangkan gelombang di dalamnya (gelombang jenis ini Anda dapat dengar di ruangan besar, atau di bawah air di saluran apa pun). Bagian dari saluran (jika kita memotongnya pada titik mana pun dari garis sepanjang dimensi panjang) akan menjadi persegi panjang lebar W dan kedalaman D. Sama seperti partikel non-kuantum, bahkan jika stasioner dari sudut pandang dimensi panjang, ia dapat bergerak sepanjang satu atau dua tambahan pengukuran (dan, dengan demikian, memiliki denyut nadi baik lebar atau kedalaman), dan gelombang akan memiliki panjang gelombang di kedua dimensi tambahan. Pembagian gelombang yang sederhana ke dalam apa yang dikerjakannya dengan mengukur lebar dan apa yang dilakukannya dengan mengukur kedalaman terutama terkait dengan segi empat saluran, dan biasanya tidak akan bekerja dalam contoh lain. Misalnya, seperti yang ditunjukkan pada gambar. 11, di bagian atas, salah satu gelombang yang diizinkan akan memiliki tiga palung untuk mengukur lebar dan satu untuk mengukur kedalaman.


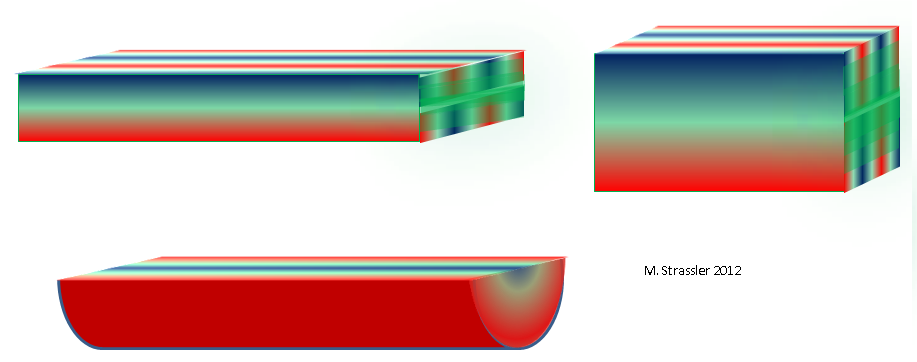Fig. 11

Kita dapat menentukan jumlah depresi dan punggungan dengan mengukur lebar dengan bilangan bulat n ₁ , dan dengan mengukur kedalaman - n ₂ , dan untuk setiap n ₁ dan n ₂ (satu atau kedua nilai ini bisa lebih besar dari nol), kita mendapatkan mitra KK. Untuk kuanta tanpa massa (m = 0) atau hampir tanpa massa, mitra KK akan memiliki massa

$$

$$M ^ 2 = m ^ 2 + (p_ {width} / c) ^ 2 + (p_ {depth} / c) ^ 2 = m ^ 2 + (n_1 h / 2 c W) ^ 2 + (n_2 h / 2 c D) ^ 2$$

Dapat dilihat bahwa distribusi massa berbeda dari kasus dengan satu dimensi tambahan, dan dapat memberi tahu kita W dan D.

Jika penampang saluran memiliki bentuk yang berbeda, misalnya, segitiga atau setengah disk, seperti yang ditunjukkan pada Gambar. 11, di bawah ini, kita mendapatkan distribusi massa lain yang mencerminkan bentuk yang tepat dari segitiga atau setengah disk. Dan kita sudah dapat membuang saluran kapal praktis dan mewakili ruang tiga dimensi, yang penampang melintangnya sesuai dengan bentuk dua dimensi terbatas lainnya, salah satunya ditunjukkan pada Gambar. 1 dalam sebuah artikel tentang dunia dengan dua dimensi spasial: cakram penuh, atau bahkan bola atau torus. Masing-masing bentuk ini akan memberi kita jenis distribusi massa mitra QC sendiri. Dan jika akan ada tiga, atau empat, atau lima dimensi tambahan ... Mungkin lebih banyak jenis distribusi.

Contoh beberapa distribusi untuk partikel tanpa massa dengan ukuran pengukuran tambahan dipilih sehingga massa mitra KK pertama adalah sama untuk setiap kasus diberikan pada Gambar. 12. Jelas bahwa untuk menetapkan bentuk dan ukuran pengukuran tambahan, perlu untuk mengukur massa dari sejumlah besar mitra KK (dan bahkan setidaknya mengkonfirmasi bahwa salah satu partikel berat yang baru ditemukan umumnya adalah mitra KK), oleh karena itu, untuk memahami sifat tambahan apa pun. pengukuran, waktu akan berlalu.


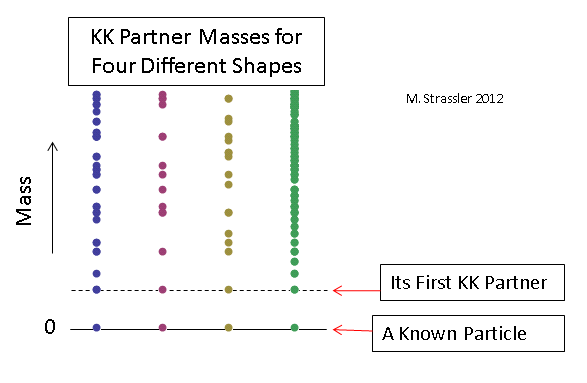Fig. 12

Tetapi bisakah diketahui partikel berat menjadi mitra KK yang lebih ringan?

Kemudian muncul pertanyaan tambahan yang jelas.Kita tahu bahwa di antara partikel-partikel unsur yang dikenal ada elektron, juga versi yang lebih berat: muon dan tau. Ada quark atas, dan versi yang lebih berat terpesona dan benar. Ada quark yang lebih rendah, dan versi yang lebih berat, aneh dan menawan. Apakah versi partikel berat merupakan mitra QC paru-paru?

Pada pandangan pertama, ini adalah asumsi yang menggiurkan, tetapi jawabannya adalah tidak. MaafIni bukan pertanyaan bodoh. Itu hanya memiliki jawaban negatif yang cerdas.

Muon dan tau, terpesona dan benar, aneh dan menawan - mereka semua mendapatkan massa berkat medan Higgs, dan bukan berkat impuls dari dimensi tambahan. Ini jelas mengikuti dari eksperimen terperinci. Tips dapat ditemukan di artikel tentang apa yang akan terjadi jika bidang Higgs nol . Harap dicatat bahwa jika bidang Higgs rata-rata nol, maka elektron, muon, dan tau tidak akan memiliki massa (dan masing-masing akan dibagi menjadi dua jenis partikel). Ini tidak sesuai dengan teori bahwa muon dan tau adalah mitra KK dari elektron.

Ada banyak alasan lain. Yang paling serius dari mereka, mungkin, adalah karena adanya muatan pada elektron dan karena fakta bahwa itu dikelilingi oleh medan listrik, foton harus bergerak dalam dimensi apa pun di mana elektron bergerak (walaupun kebalikannya tidak benar). Jadi jika elektron memiliki mitra KK, maka foton juga harus memilikinya. Tapi itu mengikuti dari rumus kami (dan yang serupa lebih umum) bahwa karena foton tidak memiliki massa, dan massa elektron (0,0005 GeV / c ² ) kecil dibandingkan dengan massa muon (sekitar 0,1 GeV / c ²), jika muon adalah mitra KK, maka foton harus memiliki mitra KK dengan massa yang sama. Tetapi partikel seperti itu, jika ada, akan ditemukan bertahun-tahun yang lalu. Faktanya, mitra KK dari foton tidak diamati dalam percobaan di mana massa dipelajari jauh lebih besar dari massa partikel Z - ini adalah ratusan GeV / s ² . Z-partikel itu sendiri juga tidak bisa menjadi mitra QC dari foton; dia tidak terlihat cukup seperti dia. Dan ini berarti setiap mitra KK dari elektron harus sekurang-kurangnya sama beratnya.

Ke mana harus pergi selanjutnya? Untuk eksperimen

Kami beralih dari teori (kemungkinan pengukuran tambahan, matematika dan geometri terkait) ke prediksi (mitra QC). Langkah selanjutnya: apa yang kita ketahui tentang pengukuran tambahan dari eksperimen? Kami belum melihat mitra KK dalam percobaan, tetapi kami mungkin bertanya, apa yang bisa kami pelajari dari ketidakhadiran mereka? Cukup banyak, seperti yang akan saya jelaskan nanti, bersama dengan deskripsi tentang bagaimana upaya untuk menemukan tanda-tanda pengukuran tambahan berlanjut di Large Hadron Collider dan di tempat lain.