Apakah alam semesta kita tidak terbatas?
Perhatian! Dalam artikel ini, hanya teori yang akan diekspresikan, tanpa bukti ilmiah.
Selamat hari Giktayms! Saya terdorong untuk menulis artikel ini dengan video YouTube tentang paradoks numerik yang tidak biasa. Yaitu, paradoks
Zeno dan mengapa tidak mungkin untuk membagi dengan nol, yang akan dibahas hari ini.
Paradoks Zeno sangat mudah dijelaskan berdasarkan
Achilles dan kura-kura. Mereka yang tidak terbiasa dengan paradoks ini, di sini adalah video visual dari penulis lain:
Saya sarankan Anda membaca sebelum membaca lebih lanjut.
(Achilles paradox dan kura-kura)Jika Anda tidak ingin menonton video, maka saya akan memberi tahu Anda secara singkat: Bayangkan bahwa Achilles mengejar seekor kura-kura yang menyusulnya. Jarak antara mereka terus menurun, karena Achilles berjalan lebih cepat dari kura-kura. Akibatnya, ketika Achilles mendekati jarak 1 meter, setelah beberapa saat akan sama dengan
0,1 meter, lalu
0,01, dan seterusnya hingga tak terbatas. Ini berarti bahwa Achilles tidak akan pernah mengejar kura-kura, tetapi dalam kenyataannya semuanya benar-benar salah.
Pada kenyataannya, tidak ada masalah, kami mengambil Achilles dan kura-kura, menaruhnya di atas treadmill dan tolong, Achilles dengan tenang menyusul penyu. Justru di sinilah letak bukti yang mungkin bahwa alam semesta tidak terbatas.
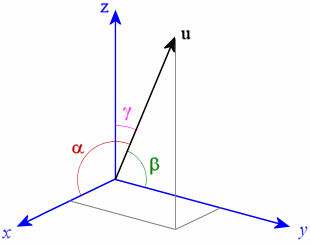(Vektor dalam ruang 3D)Mari kita coba jelaskan ini pada prinsip permainan komputer. Biasanya, posisi suatu objek ditulis sebagai vektor yang terdiri dari sumbu x, y, dan z. Dan setiap nilai disimpan dalam tipe data
float (nilai floating point) . Misalnya,
Unity3D menggunakan float 32-bit untuk menunjukkan posisinya di ruang angkasa. Nilai minimumnya yaitu:
1.175494351 E - 38. , yang memberikan pergerakan mulus di hampir semua skala. Di sini kata yang penting adalah
"hampir" , yaitu, jika kita sangat mengurangi dan mendekati model, kita akan melihat bagaimana itu bergerak dalam lompatan. Melompat dari
0, ... 1 ke
0, ... 2 ke
0, ... 3 , dll. Ini berarti bahwa dalam simulasi, dalam skenario apa pun, Achilles akan menyusul penyu. Tetapi seperti yang mereka katakan tidak ada kejahatan tanpa kebaikan. Jika kita memiliki nilai float minimum, maka ada batas ruang
3D maksimum. Melampaui itu kita tidak akan diizinkan
(sebut saja) hukum fisika dunia maya. Pada kenyataannya, kita tidak bisa memberikan lebih dari nilai maksimum suatu variabel.
Jika kita kembali ke paradoks Zeno, Achilles tidak hanya tidak akan pernah bisa mengejar kura-kura, tetapi tidak akan pernah mencapai batas dunia fantasinya, baginya dia akan menjadi tak terbatas. Dari -∞ hingga + ∞, anehnya, kita mendapatkan fungsi yang sama
f (x) = 1 / x . Dan yang paling lucu adalah bahwa nilai
x / 0 tidak termasuk dalam fungsi ini, karena fungsi tersebut tidak akan pernah mencapai nol, seperti Achilles the tortoise.
(Sebenarnya, ini tidak dapat dibagi dengan nol)Cukup teori, mari kita berlatih. Ambil dunia nyata, kita semua terdiri dari atom, atom terdiri dari proton dan elektron neutron, yang pada gilirannya terdiri dari quark
(partikel elementer) . Baik dalam simulasi maupun di dunia nyata, Achilles tidak perlu menyalip kura-kura. Semua ini mengarah pada fakta bahwa, baik dalam simulasi maupun dalam kenyataan, partikel elementer juga harus melonjak dengan angka
0, ... 1 0, ... 2 0, ... 3 karena hal ini terjadi dalam permainan, karena Achilles dapat menyalip kura-kura di sana-sini. Ini memberi tahu kita bahwa paradoks Zeno hanya bekerja di atas kertas, atau dalam sistem koordinatnya, yang nilainya dari -∞ hingga + ∞. Pada kenyataannya, melompat pada nilai terkecil, partikel elementer Achilles pada suatu saat menyalip penyu, koordinatnya menjadi sama, setelah Achilles berlari maju.
Jadi kami belajar sistem koordinat apa yang digunakan ruang kami, mari kembali ke topik utama. Jika kita memiliki nilai minimum, maka akan ada batas maksimum -
tepi alam semesta kita . Ada orang-orang yang akan mengatakan mengapa, di satu sisi, itu bisa tak terbatas, dan di sisi lain, terbatas. Tetapi masalahnya adalah bahwa koordinat atau posisi hanya merupakan elemen dari sistem besar yang disebut ruang, dan itu bisa sepenuhnya tak terbatas atau sepenuhnya terbatas. Juga, ini semua menimbulkan pertanyaan, dan kebetulan kita tidak dalam simulasi komputer, ya? Tapi ini topik untuk artikel lain.
Ringkasan
Jadi hari ini kita sampai pada kesimpulan bahwa alam semesta
TIDAK tanpa batas, dalam postingan ini hanya teori yang diungkapkan bagaimana tidak ada yang benar-benar mengetahui alam semesta di sana, dan tidak dapat membuktikannya. Tapi mungkin dengan artikel ini, saya mendorong seseorang untuk membuat penemuan baru.
Sumber